考虑页岩气扩散的多级压裂水平井产能模型

田 冷，肖 聪，刘明进，顾岱红

(1.中国石油大学(北京)石油工程学院，北京 102249； 2.西南石油大学地球科学与技术学院，四川成都 610500)

考虑页岩气扩散的多级压裂水平井产能模型

田 冷1，肖 聪1，刘明进2，顾岱红1

(1.中国石油大学(北京)石油工程学院，北京 102249； 2.西南石油大学地球科学与技术学院，四川成都 610500)

由于存在浓度差，在多级压裂水平井中，页岩气由基质孔隙同时向天然裂缝和人工裂缝扩散.基于三孔块状模型，考虑页岩气解吸、扩散、渗流，建立页岩气多级压裂水平井产能模型；应用拉普拉斯变换，获得拉氏空间产量解，结合stehfest数值反演，绘制页岩气典型试井曲线.结果表明，考虑双扩散页岩气的流动过程分为线性流、拟稳定窜流、由基质向天然裂缝扩散、由基质向人工裂缝扩散和边界控制流5个主要流动阶段；拟稳态扩散条件下，压力导数受孔隙体积倍数变化影响敏感；扩散系数越大，气体扩散越早；兰格缪尔参数越大，气体解吸和供气能力越强；压裂级数越多，窜流系数越大，天然裂缝向人工裂缝窜流越早.通过与实际生产数据拟合，验证模型合理性，研究结果对认识页岩气藏压裂水平井产能递减规律、预测产能及优化压裂参数具有参考意义.

页岩气；压裂水平井；产能模型；解吸；双扩散；典型曲线

0 引言

体积压裂改造型页岩气藏气体流动方式及机理[1-8]较为复杂，研究中多将页岩储层简化为双重孔隙或三重孔隙模型.针对页岩气双孔流动模型，Barenblatt G I等提出页岩气双孔(基质孔隙和裂缝)拟稳态流动模型[9]，Warren J E等对此模型加以完善，提出不稳定流动模型[10]，但他们未考虑页岩气解吸、扩散对产能的影响；Zhao Yulong、Wang Haitao、任俊杰等给出页岩气双孔球形流模型，运用点源函数和势叠加原理，同时考虑页岩气解吸扩散影响，分析产能影响因素[11-13]，但模型中人工裂缝为无限导流裂缝，与实际页岩气藏压裂水平井流动方式不符；Al-Ghamdi A、El-Banbi A H等提出页岩气三孔(双缝、单基质)流动模型[14-15]，通过分析实际生产曲线发现，页岩气生产中线性流动占主导地位，El-Banbi A H提出线性三孔模型，并给出拉普拉斯空间解，但没有考虑页岩气解吸和扩散影响；Hasan A等提出考虑页岩气解吸和扩散影响的三孔线性流动模型[16]，但模型仅考虑吸附气向天然裂缝扩散情况，忽略基质气体向人工裂缝的扩散；Ezulike D O等提出考虑基质气体同时向天然裂缝和人工裂缝窜流的三孔线性流动模型[17]，但忽略页岩气解吸和扩散影响.由于基质中气体存在浓度差，现有页岩气三孔线性流动模型，还未见同时考虑向天然裂缝和人工裂缝扩散的研究.

文中基于三孔块状模型，考虑页岩气解吸、双扩散和渗流，建立定产量页岩气多级压裂水平井产能模型，应用拉普拉斯变换，获得拉氏空间产量解，结合stehfest数值反演，绘制页岩气典型试井曲线，分析各种产能影响因素.

1 流动特征及产能模型

1.1 流动特征

1.1.1 吸附效应

人们主要通过兰格缪尔等温吸附方程描述页岩气在基质表面吸附效应[2]，表示为

式(1-2)中：Va为吸附体积；VL为兰格缪尔体积；p为地层压力；pL为兰格缪尔压力；ψL为兰格缪尔拟压力；ψ为地层拟压力.

1.1.2 扩散效应

一般情况下，页岩气扩散流动满足Fick扩散定律，气体从高浓度向低浓度扩散，可根据基质孔隙中气体浓度分布状态，分别由Fick第一定律和第二定律表示.

Fick第一定律表示每个时刻基质块中各处气体浓度相等，气体扩散速度与内外浓度差呈线性关系[4]，扩散方程为

考虑气体拟压力形式下的等温吸附方程为

式(3-4)中：V为气体浓度；t为时间；Fs为基质块的形状因子；D为气体扩散系数；VE为裂缝壁面气体浓度；φm为基质孔隙度.

1.2 物理模型

将页岩气压裂地层简化为块状模型(见图1)，其中，LF、Lf为基质块的长和宽；Lh为水平井井筒长度；Le为人工裂缝半长.考虑矩形封闭地层中心一口水平井定产量生产时，假设条件：(1)初始条件下，地层压力为pi，储层具有双孔介质(基质孔隙和天然裂缝孔隙)特征；(2)人工裂缝垂直于井筒并贯穿储层，相对井筒对称并均匀分布，天然裂缝与人工裂缝垂直，气藏的长度、宽度分别与水平井井筒长度和人工裂缝长度相等；(3)人工裂缝具有有限导流能力，人工裂缝和天然裂缝中流体渗流符合达西定律，基质孔隙中气体为扩散流动；(4)气体由基质同时向人工裂缝和天然裂缝扩散，从天然裂缝向人工裂缝窜流，仅从人工裂缝向井筒供气；(5)页岩气和地层岩石微可压缩，压缩系数恒定；(6)页岩气吸附规律满足兰格缪尔等温吸附方程，扩散规律满足Fick定律；(7)气体渗流过程忽略毛管力和重力影响.

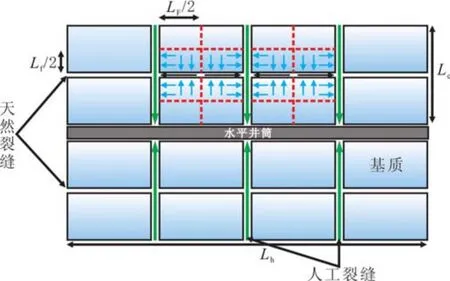
图1 多级压裂水平井流动模型Fig.1 The flow model of multi-stage fracturing horizontal well

Fick第二定律表示基质块中气体浓度分布为时间和位置的函数[4]，扩散方程为

1.3 数学模型

页岩气在基质孔隙中同时向天然裂缝和人工裂缝扩散，根据气体扩散方向，将基质分为气体由基质向人工裂缝扩散和由基质向天然裂缝扩散2部分.定义基质孔隙体积倍数χ=φma/φm，表示裂缝扩散气体所在的基质孔隙占总基质孔隙的体积比，其中，φma为裂缝占基质体积的孔隙度；φm为总基质的孔隙度.基质中向人工裂缝和天然裂缝扩散气体的扩散系数分别为D1和D2，表示基质中气体向不同裂缝扩散能力的大小.

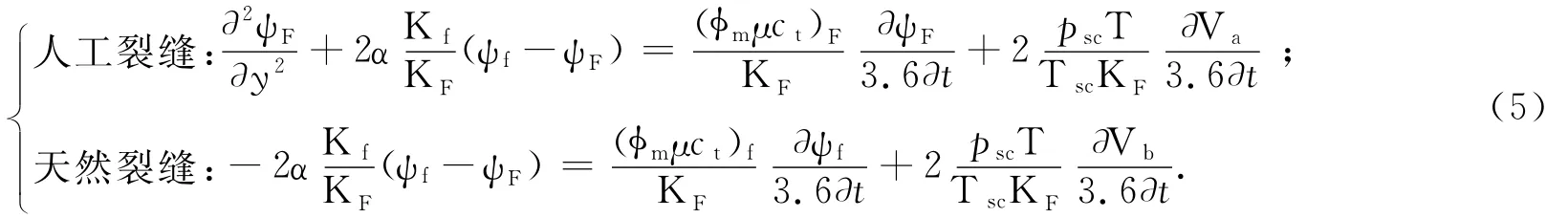
气体由天然裂缝向人工裂缝的渗流方式为拟稳态窜流，人工裂缝中流体具有限导流能力，流动满足线性流动规律.由质量守恒定律，页岩气井定产量条件下基质、天然裂缝和人工裂缝中流动方程联立求解并拟压力化，得到气体在不同裂缝中的扩散方程：式中：ψF、ψf为人工裂缝和天然裂缝中气体的拟压力；x、y为气体流动距离；α为形状因子；kF、kf为人工裂缝和天然裂缝的渗透率；φj(j=F，f)为人工裂缝或天然裂缝孔隙度；μ为气体黏度；ct为岩石总压缩系数；t为气体流动时间；Va、Vb为由基质向人工裂缝和天然裂缝中扩散的气体浓度；psc为地面标准状况下的压力；T为储层温度；Tsc为地面标准状况下的温度.

将基质中气体向人工裂缝和天然裂缝中扩散方式分为4类，讨论基质中气体拟稳态和非稳态扩散的控制方程.

(1)扩散方式Ⅰ，基质中气体向人工裂缝和天然裂缝中扩散方式为拟稳态扩散：

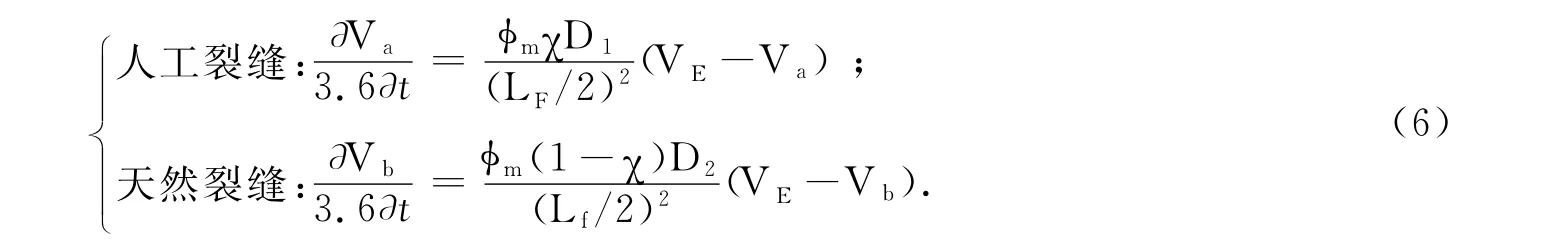
(2)扩散方式Ⅱ，基质中气体向人工裂缝和天然裂缝中扩散方式为非稳态扩散：

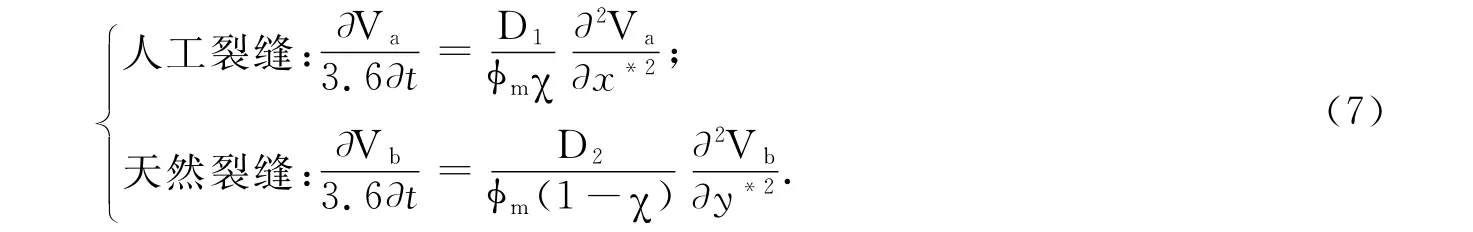
(3)扩散方式Ⅲ：基质中气体向人工裂缝中扩散方式为拟稳态、向天然裂缝中扩散为非稳态方式：

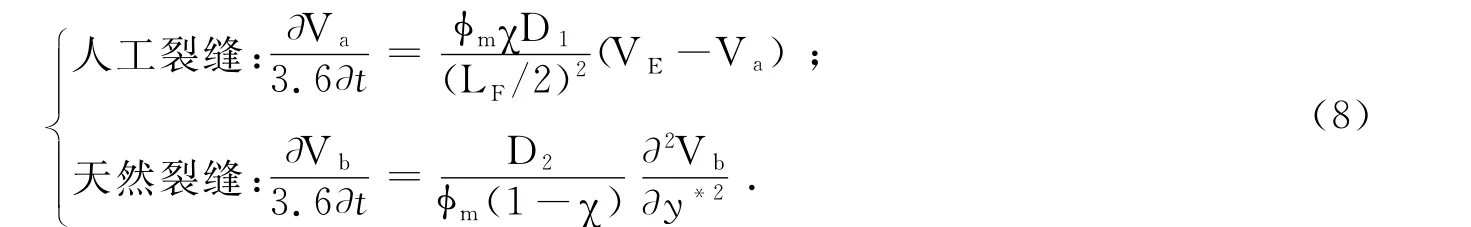
(4)扩散方式Ⅳ：基质中气体向人工裂缝中扩散方式为非稳态、向天然裂缝中扩散为拟稳态方式：

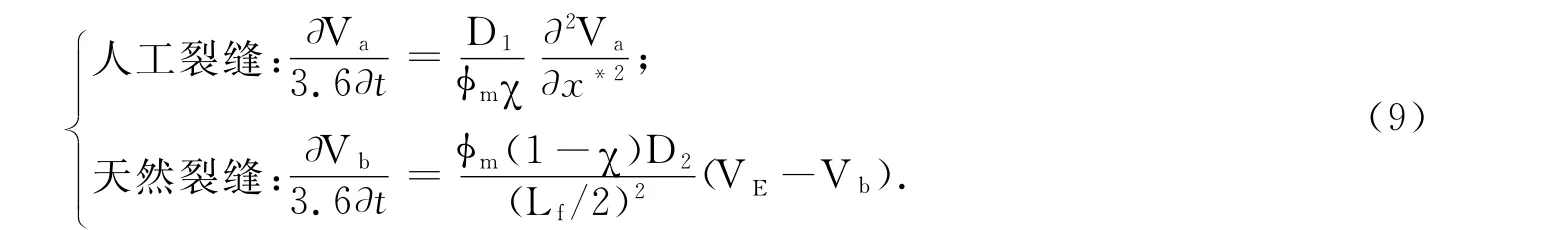
对于非稳态扩散气体，基质向人工裂缝和天然裂缝的气体扩散浓度随时间的变化量分别表示为

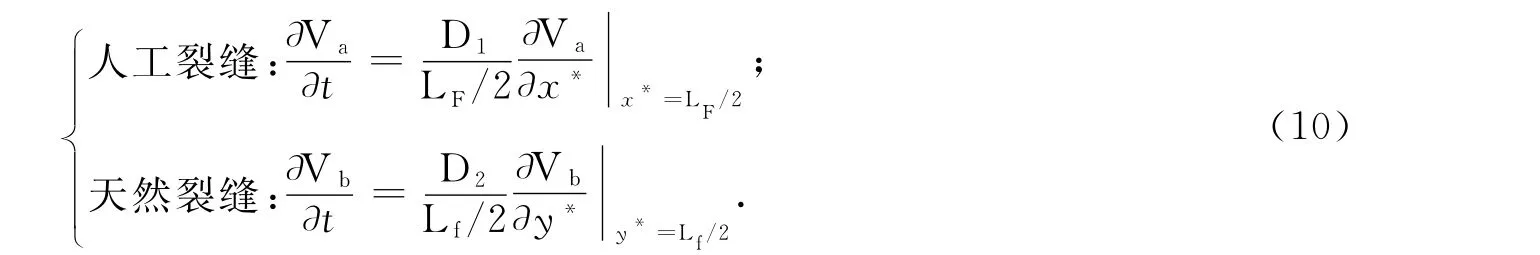
将式(5-10)无因次化，得到气体在不同裂缝中的无因次扩散方程：

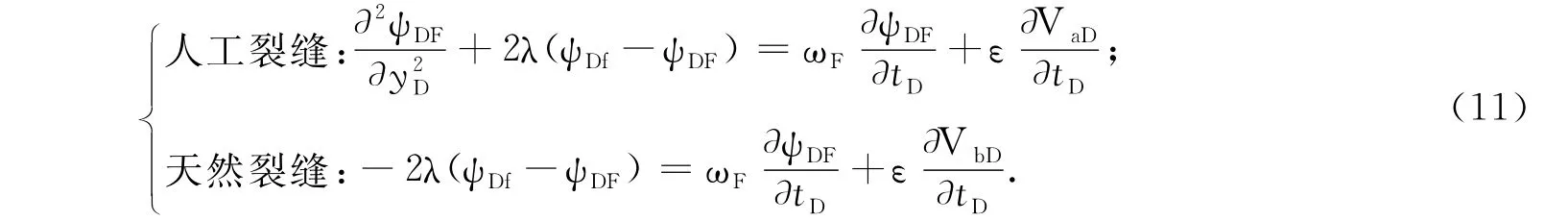
基质中气体以不同扩散方式向人工裂缝和天然裂缝扩散时的无因次扩散方程分别为

(1)扩散方式Ⅰ：

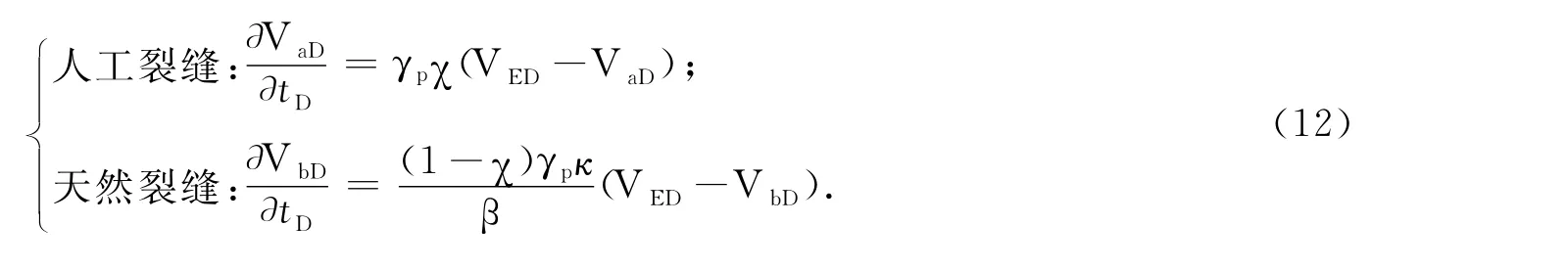
(2)扩散方式Ⅱ：

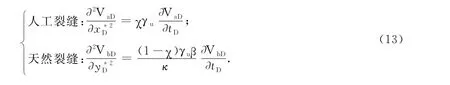
(3)扩散方式Ⅲ：

(4)扩散方式Ⅳ：

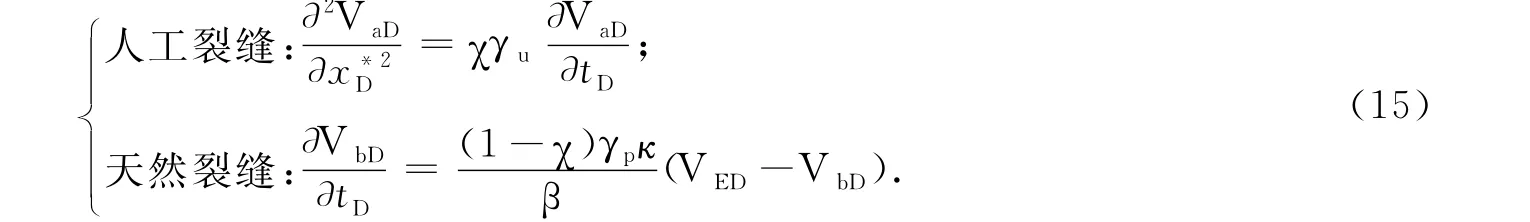
对于非稳态扩散气体，基质向人工裂缝和天然裂缝的气体扩散浓度随时间的变化量分别表示为

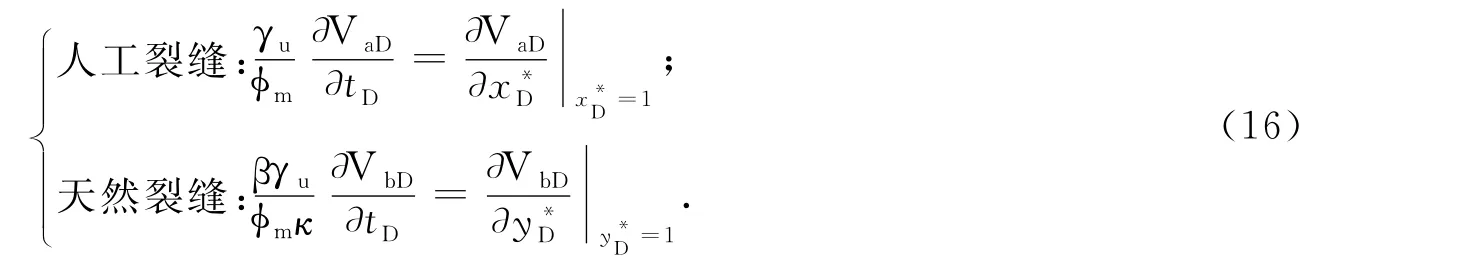
控制方程的初始条件为

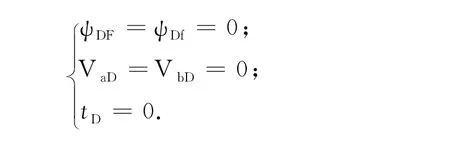
2 模型求解

采用常规计算方法难以求得产能控制方程的解析解，需对产能控制方程进行拉普拉斯变换得到它在拉氏空间中的方程，s表示拉普拉斯因子.

将式(11)经过拉普拉斯变换，得到气体在不同裂缝中扩散的拉氏空间方程：

人工裂缝边界条件为

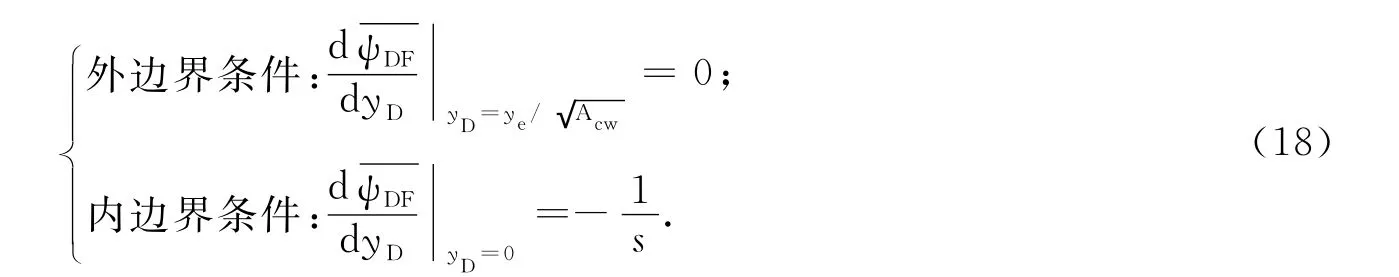
基质中气体以不同扩散方式向人工裂缝和天然裂缝扩散时的拉氏空间方程为

(1)扩散方式Ⅰ：

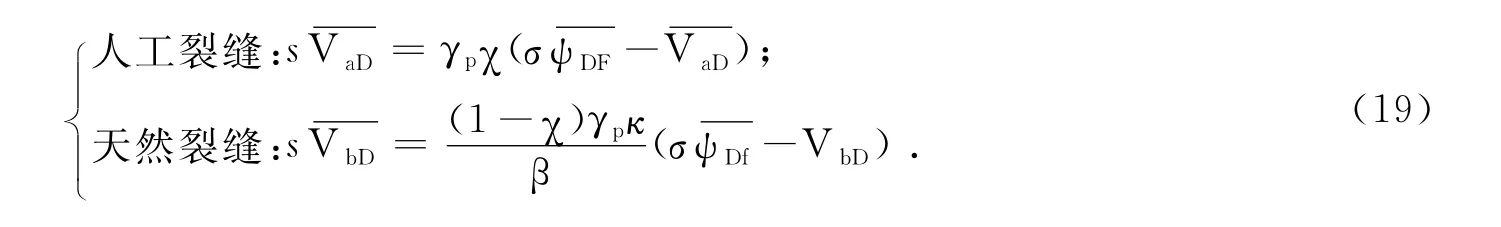
(2)扩散方式Ⅱ：

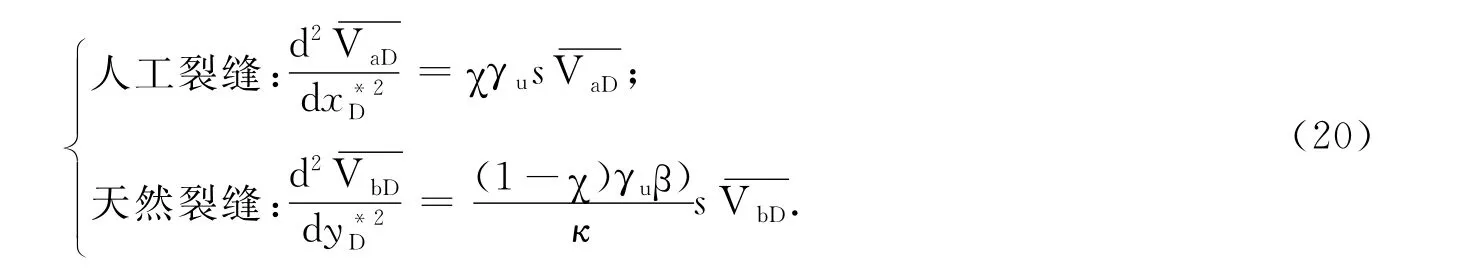
(3)扩散方式Ⅲ：

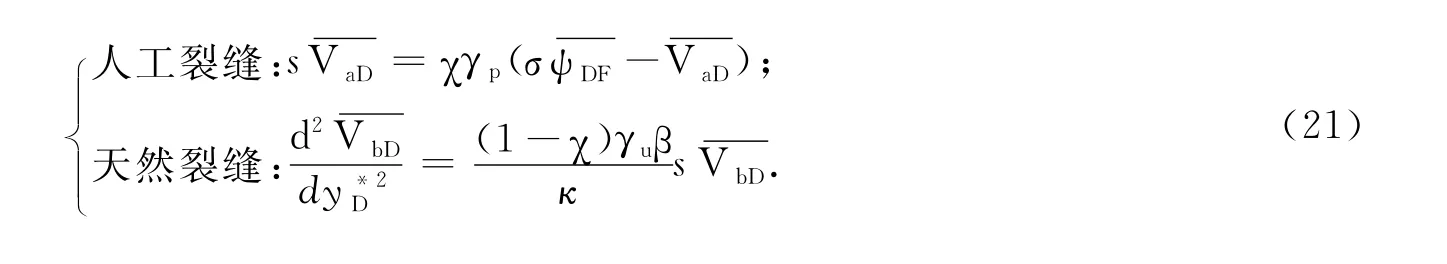
(4)扩散方式Ⅳ：

非稳态边界条件为

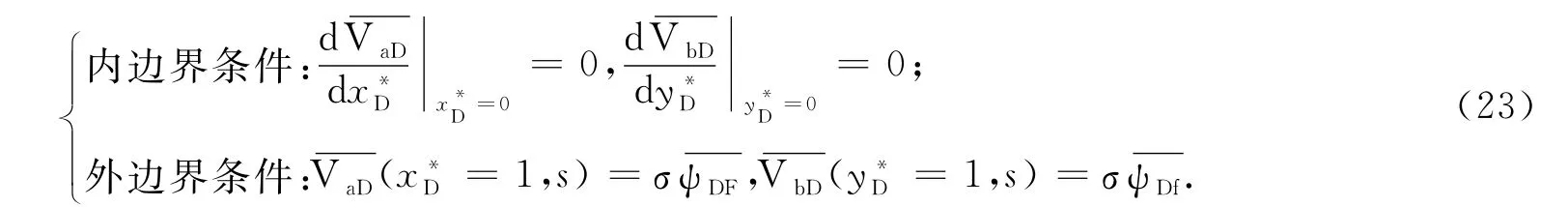
对4种扩散条件下的基质方程(式(19-22))求解，分别为

(1)扩散方式Ⅰ：

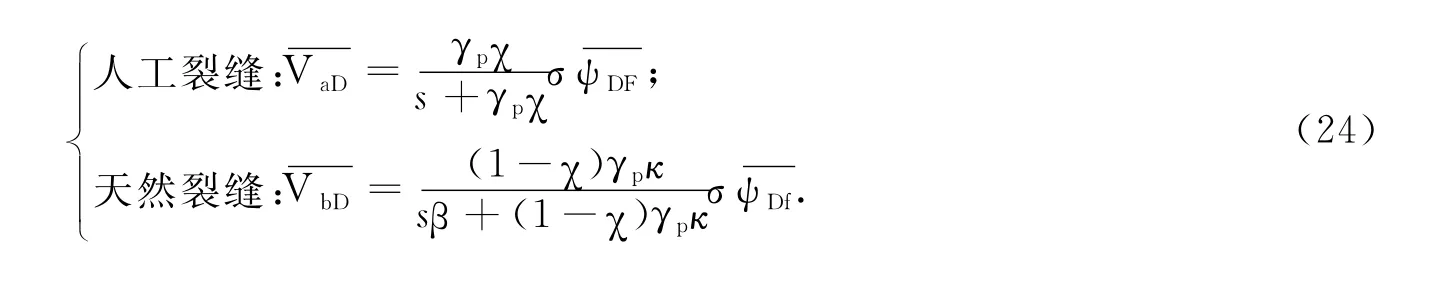
(2)扩散方式Ⅱ：

(3)扩散方式Ⅲ：

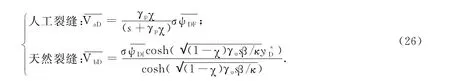
(4)扩散方式Ⅳ：

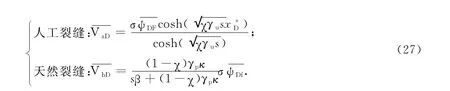
3 典型曲线及压力影响因素

结合stehfest数值反演得到实空间页岩气多级压裂水平井定产量条件下的解，绘制实空间无因次拟压力/压力导数和无因次产量/产量导数随无因次时间的变化关系曲线(见图2)，划分流体流动阶段，分析影响因素.其中参数设置：裂缝窜流系数λ=54，ω=0.032，κ=19.75，γu=0.047，γp=1.339，σ=4.4× 10-4，β=1；实线表示无因次拟压力(或产量)曲线，虚线表示无因次拟压力导数(或产量导数)曲线.

3.1 流动阶段

绘制并分析基质中气体以不同扩散方式向天然裂缝和人工裂缝扩散时的典型试井曲线(见图2)，将不同扩散方式下页岩气流动分为5个流动阶段.

(1)流动阶段Ⅰ.为人工裂缝中早期线性流阶段；拟压力导数曲线和拟压力曲线平行，斜率为0.5，无因次产量曲线斜率等于-0.5，人工裂缝外地层中的气体未发生流动.

(2)流动阶段Ⅱ.为天然裂缝向人工裂缝拟稳定窜流阶段；拟压力导数曲线和产量导数曲线出现下凹形状，由于人工裂缝中压力降低，天然裂缝中压力与之形成压力差，形成窜流.

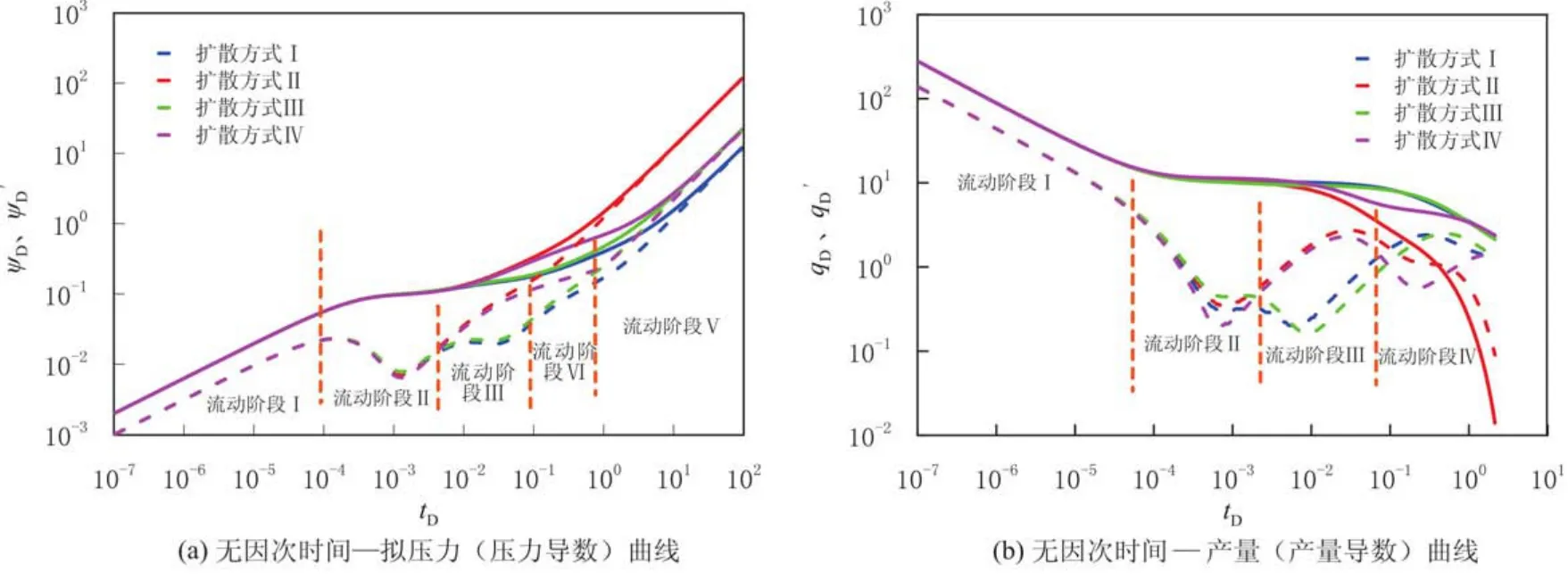
图2 不同扩散方式下试井典型曲线Fig.2 The type curves with different diffusion patterns

(3)流动阶段Ⅲ.为基质中气体向天然裂缝扩散阶段；分别考虑气体拟稳态扩散和非稳态扩散情况：拟稳态扩散条件下，拟压力导数曲线出现下凹；非稳态扩散条件下，拟压力和压力导数曲线近乎平行，斜率约为0.5，无因次产量曲线斜率约为-0.5，表明基质气体中为线性流动，通过扩散向天然裂缝中供气.

(4)流动阶段Ⅳ.为基质中气体向人工裂缝扩散阶段.分别考虑气体拟稳态扩散和非稳态扩散情况：拟稳态扩散条件下，拟压力导数曲线出现下凹，但下凹程度不明显；非稳态扩散条件下，拟压力和压力导数曲线近乎平行，斜率约为0.5，表明基质中气体为线性流动，通过扩散向人工裂缝中供气.

(5)流动阶段Ⅴ.为边界控制流阶段.压力波到达气藏边界，拟压力和压力导数曲线上翘，最终趋于重合.

3.2 压力影响因素

3.2.1 不同扩散方式下的基质孔隙体积倍数

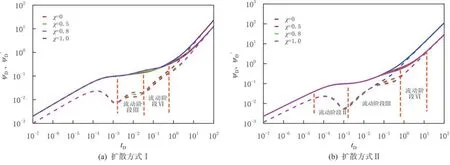
图3 不同扩散方式下基质孔隙体积倍数对页岩气典型曲线的影响Fig.3 The impacts of matrix pore volume ratio on type curves with different diffusion patterns

绘制两种扩散方式下，基质孔隙体积倍数χ分别为0、0.5、0.8、1.0时的无因次拟压力和压力导数曲线(见图3).扩散方式Ⅰ见图3(a)，χ=0和χ=1分别表示基质中气体向天然裂缝和人工裂缝扩散情况，拟压力导数曲线上只出现两个下凹(拟稳定窜流和拟稳态扩散).当χ≠0时，拟压力导数曲线出现两个扩散下凹段(向人工和天然裂缝均为拟稳态扩散)，随着χ的增大，基质向人工裂缝中的扩散量增大.扩散方式Ⅱ见图3(b)，拟压力导数曲线只出现一个下凹段(拟稳定窜流段)，后出现斜率为0.5的非稳态扩散线性流阶段，随着χ的增大，拟压力导数曲线后期上移.对比图3(a)和图3(b)，两种扩散方式下，压力响应差异较大，拟稳态扩散条件，压力导数随χ变化较为敏感，且基质中气体向天然裂缝中拟稳态扩散比向人工裂缝中拟稳态扩散时，边界导致的压力下降大(拟压力曲线上移)，原因是基质对人工裂缝中的气体补充，使压力降低变慢，压力波到达边界时间延长；相反，当基质中气体向天然裂缝扩散时，人工裂缝压力降低不能得到补充，使边界影响变大.

3.2.2 基质中气体向不同裂缝拟稳态扩散时的无因次扩散系数比

绘制基质中气体以不同扩散系数比β分别向人工裂缝和天然裂缝中拟稳态扩散时的无因次拟压力和压力导数曲线(见图4).图4(a)中，D1=300 m3/m3，分别取D2=600、300、150 m3/m3，得到β=0.5、1和2；图4(b)中，D2=300 m3/m3，分别取D1=150、300、600 m3/m3，得到β=0.5、1、2.由图4可见，扩散系数是表征气体扩散早晚及难易程度的参数，扩散系数越大，扩散越容易发生，拟稳态窜流特征越明显，基质中气体向天然裂缝中拟稳定扩散发生越早；基质中气体向人工裂缝中非稳态扩散基本不受扩散系数的影响.

图4 基质中气体向不同裂缝拟稳态扩散时无因次扩散系数比对页岩气典型曲线的影响Fig.4 The impacts of dimensionless diffusion parameter ratio on type curves

3.2.3 基质中气体向不同裂缝拟稳态扩散时的吸附系数

绘制基质中气体以不同吸附系数σ向人工裂缝和天然裂缝下拟稳态扩散时的无因次拟压力和压力导数曲线(见图5).图5(a)中，VL=10 m3/m3，分别取pL=3、5、8 MPa，得到σ=0.000 34、0.000 88、0.001 89；图5(b)中，pL=8 MPa，分别取VL=10、15、20 m3/m3，得到σ=0.001 89、0.002 85、0.003 79.由图5可知，吸附系数是表征气体解吸程度的参数，拟稳态扩散典型曲线形成凹槽，随着pL增大，气体压力降低，发生解吸越早，随着VL增大，气体吸附浓度增大，两者同时作用导致吸附系数σ增大，典型曲线下凹程度加大.由于气体解吸，基质气体浓度增大，使基质内外浓度差增大，气体向裂缝中扩散越早，流动后期解吸气对裂缝进行补充，边界控制流阶段气体压力降低减慢，压力传播到边界时间变长，边界控制流阶段影响变小.

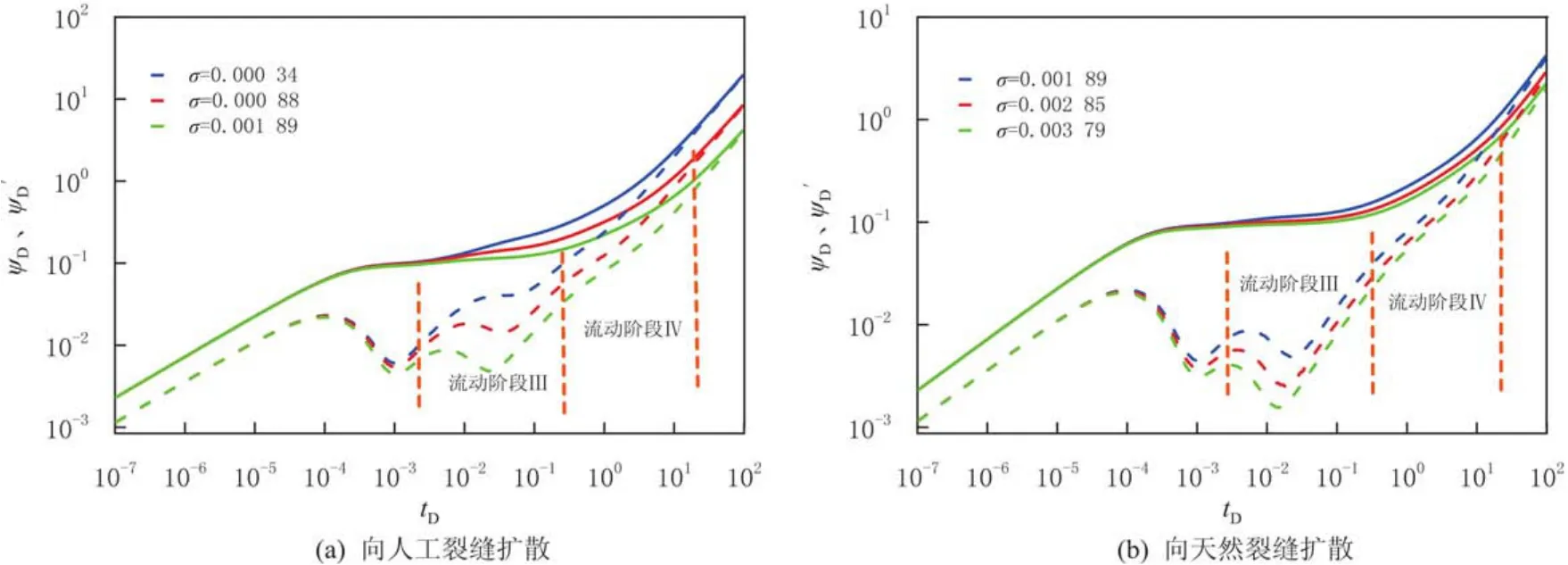
图5 基质中气体向不同裂缝拟稳态扩散时的无因次吸附系数对页岩气典型曲线的影响Fig.5 The impacts of dimensionless adsorption parameter on type curves

3.2.4 基质中气体以扩散方式Ⅳ向不同裂缝扩散时的窜流系数

绘制基质中气体以扩散方式Ⅳ、用不同裂缝窜流系数λ向不同裂缝扩散时的无因次拟压力和压力导数曲线(见图6)，其中气体向人工裂缝中扩散时为非稳态扩散，向天然裂缝中扩散时为拟稳态扩散.人工裂缝条数下HF=8、10、15时，基质单元尺寸比κ=69.40、44.40、19.75.κ反映裂缝的密度，它影响基质块的形状因子，得到不同窜流系数λ(λ=15.36、24.00、54.00).由图6可见，随着人工裂缝条数的增大，基质单元尺寸比减小，基质块窜流系数变大，使天然裂缝向人工裂缝中窜流发生得越早，拟稳定窜流段凹槽整体左移；当窜流系数过小时，曲线上观察不到拟稳定窜流阶段.

4 实例验证

根据四川长宁—威远页岩气区某压裂水平井实际生产数据，绘制无因次产量/产量导数和时间的双对数典型试井曲线(见图7).其中实线为理论曲线、散点为实测生产数据.选择χ≠0时的典型试井曲线图版，对理论曲线和实测曲线进行拟合，拟合结果较好.

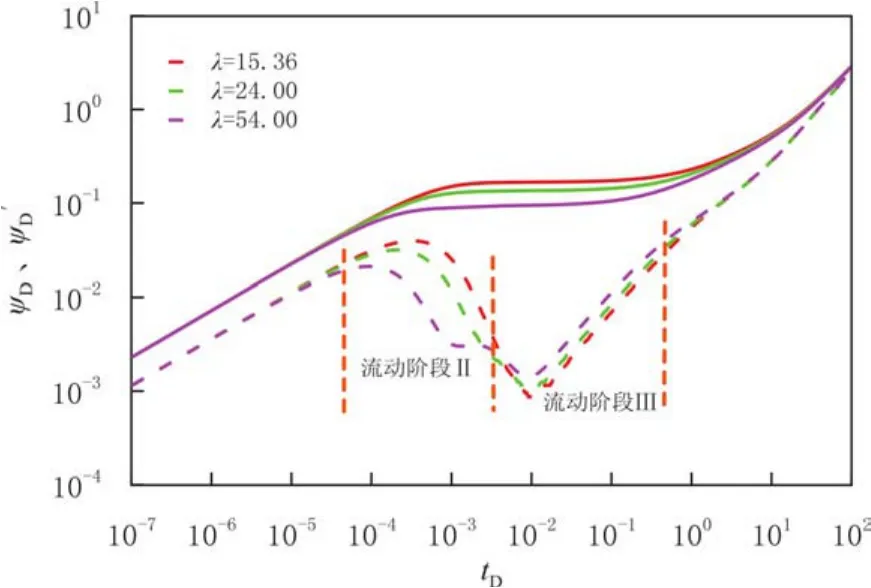
图6 基质中气体以扩散方式Ⅳ向不同裂缝扩散时窜流系数对页岩气典型曲线的影响Fig.6 The impacts of dimensionless inter-porosity parameter on type curves

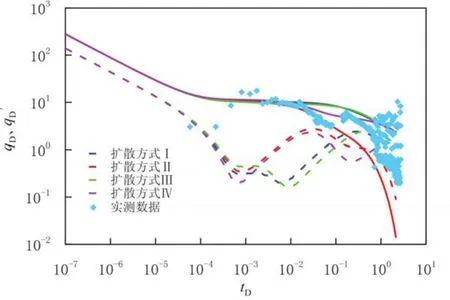
图7 理论模型和实际生测数据拟合结果Fig.7 The matching result between theortical model and real data

由图7可见，在页岩气流动过程中，该页岩气井基质中气体的扩散方式为：气体向人工裂缝中拟稳态扩散，向天然裂缝中非稳态扩散.孔隙体积倍数χ不同，曲线的特征和趋势不变.表明文中理论模型可用于实际生产中页岩气藏流动方式的判断.因此，结合实际生产数据，可以通过该理论模型典型试井曲线图版初步拟合并确定基质中气体分别向不同裂缝的扩散方式，进而精细拟合确定孔隙体积倍数.

5 结论

(1)建立考虑解吸、扩散、渗流的页岩气多级压裂水平井产能分析物理和数学模型，并求出解析方程.

(2)考虑基质中气体向不同裂缝扩散的4种扩散方式：向人工裂缝和天然裂缝中扩散方式均为拟稳态扩散；向人工裂缝和天然裂缝中扩散方式均为非稳态扩散；向人工裂缝中扩散方式为拟稳态、向天然裂缝中扩散为非稳态扩散；向人工裂缝中扩散方式为非稳态、向天然裂缝中扩散为拟稳态扩散.气体流动划分为5个阶段：人工裂缝中早期线性流阶段；天然裂缝向人工裂缝拟稳定窜流阶段；基质向天然裂缝扩散阶段；基质向人工裂缝扩散阶段；边界控制流阶段.

(3)不同扩散方式下，基质孔隙体积倍数对压力影响差异较大：拟稳态扩散条件，压力导数随其变化较敏感，仅考虑基质向天然裂缝拟稳态扩散比仅考虑基质向人工裂缝拟稳态扩散，边界导致的压力下降大.可以根据压力响应情况，推测地层气体扩散方式，从而进行产能预测.与拟稳定窜流特征类似，扩散系数和兰格缪尔系数是反映拟稳态扩散的两个相关特征参数.扩散系数反映气体扩散能力大小，扩散系数越大，气体扩散越早发生；兰格缪尔参数反映基质解吸和储存吸附气的能力大小，参数越大，气体的解吸和供气能力越强.

(4)对于页岩气多级压裂水平井，宏观压裂级数影响微观基质形状因子，最终影响窜流系数，压裂级数越多，窜流系数越大，天然裂缝越早向人工裂缝发生窜流，页岩气产量越高.

[1] 单衍胜，张金川，李晓光，等.辽河盆地东部凸起太原组页岩气聚集条件及有利区预测[J].东北石油大学学报，2012，36(1)：1-7.

Shang Yansheng，Zhang Jinchuan，Li Xiaoguang，et al.Shale gas accumulation factors and prediction of favarable area of Taiyuan Formation in Liaohe Eastern Uplift[J].Journal of Northeast Petroleum University，2013，36(1)：1-7.

[2] 郭为，熊伟，高树生，等.页岩气等温吸附/解吸特征[J].中南大学学报：自然科学版，2013，44(7)：2836-2840.

Guo Wei，Xiong Wei，Gao Shusheng，et al.Isothermal adsorption/desorption characteristics of shale gas[J].Journal of Central South University：Science and Technilogy，2013，44(7)：2837-2840.

[3] 杨镱婷，张金川，王香增，等.陆相页岩气的泥页岩评价——以延长下寺湾区上三叠统延长组长7段为例[J].东北石油大学学报，2012，36(4)：10-17.

Yang Yiting，Zhang Jinchuan，Wang Xiangzeng，et al.Source rock evaluation of continental shale gas：A case study of Chang 7 of Mesozoic Yanchang Formation in Xia Siwan area of Yanchang[J].Journal of Northeast Petroleum University，2012，36(4)：10-17.

[4] 李清泉，王新海，尹虎，等.页岩气藏数值模拟及井底压力动态分析[J].东北石油大学学报，2013，37(1)：91-96.

Li Qingquan，Wang Xinhai，Yi Hu，et al.Simulation of shale gas reservoirs and dynamic analysis of bottom hole pressure[J].Journal of Northeast Petroleum University，2013，37(1)：91-96.

[5] 温庆志，李杨，胡蓝霄，等.页岩储层裂缝网络导流能力实验分析[J].东北石油大学学报，2013，37(6)：55-62.

Wen Qingzhi，Li Yang，Hu Lanxiao，et al.Experimental analysis of the flow conductivity of the nettwork-like fractures in shale reservoirs[J].Journal of Northeast Petroleum University，2013，37(6)：55-62.

[6] 王树平，史云清，严谨，等.考虑裂缝干扰的气藏压裂水平井产能预测模型[J].大庆石油学院学报，2012，36(3)：67-71.

Wang Shuping，Shi Yunqing，Yan Jin，et al.A new productivity prediction model of fracturing horizontal well in gas reservoir tajing into account the mutual interference between the fractures[J].Journal of Daqing Petroleum Institute，2012，36(3)：67-71.

[7] 刘洪林，王红岩.中国南方海相页岩吸附特征及其影响因素[J].天然气工业，2012，32(9)：5-9.

Liu Honglin，Wang Hongyan.Adsorptivity and influential factors of marine shales in South China[J].Natural Gas Industry，2012，32(9)：5-9.

[8] 魏明强，段永刚，方泉唐，等.页岩气藏孔渗结构特征和渗流机理研究现状[J].油气藏评价与开发，2011，1(4)：73-76.

Wei Mingqiang，Duan Yonggang，Fang Quantang，et al.Current research situation of porosity&permeability characteristics and seepage mechanism of shale gas reservoir[J].Reservoir Evaluation and Development，2011，1(4)：73-76.

[9] Barenblatt G I，Zhelto I P，Kochina.Bacis concepts of the theory of seepage of homogeneous liquids in fissured rocks[J].Journal of Applied Mathematical Mechanics，1960，24(5)：852-864.

[10] Warren J E，Root P J.The behavior of naturally fractured reservoirs[J].SPE J，1963，3(3)：245-255.

[11] Zhao Yulong，Zhang Liehui，Zhao Jinzhou，et al.Triple porosity modeling of transient well test and rate decline analysis for multifractured horizontal well in shale gas reservoir[J].Journal of Petroleum Science and Engineering，2013，110：253-262.

[12] Wang Haitao.Performance of multiple fractured horizontal wells in shale gas reservoir with consideration of multiple mechanisms [J].Journal of Hydrology，2014，18：467-473.

[13] 任俊杰，郭平，王德龙，等.页岩气藏压裂水平井产能模型及影响因素[J].东北石油大学学报，2012，36(6)：76-81.

Ren Junjie，Guo Ping，Wang Delong，et al.Productivity model of fractured horizontal wells in shale gas reservoirs and analysis of influential factors[J].Journal of Northeast Petroleum University，2012，36(6)：76-81.

[14] Al-Ghamdi A，Ershaghi I.Pressure transient analysis of dually fractured reservoirs[J].SPE J，1996：23-25.

[15] El-Banbi A H.Analysis of tight gas wells.Ph.D.Dissertation[D].Texas：Texas A&M University，1998.

[16] Hasan A，Al-Ahmadi，Armaco S，et al.Triple-porosity model：One further step toward capturing fractured reservoirs heterogeneity [J].SPE-SAS-1096.

[17] Obinna E D，Hassan D.A model for simultaneous matrix depletion into natural and hydraulic fracture network[J].Journal of Natural Gas Science and Engineering，2014，16：57-69.

TE33

A

2095-4107(2014)05-0093-10

DOI 10.3969/j.issn.2095-4107.2014.05.012

2014-06-26；编辑张兆虹

国家自然科学基金项目(51204193)

田 冷(1977-)，男，博士，副教授，主要从事油气田开发方面的研究.