封闭结构三能级原子系统中的压缩和纠缠特性
2014-10-09候邦品
陈 静, 候邦品
(四川师范大学物理与电子工程学院,四川成都610066)
1 预备知识
压缩和纠缠是表征光场量子特性的重要物理量.与相干态相比,压缩态能够提高信噪比,因此在量子信息和量子计算中有广泛的应用[1-4].正因如此,对压缩和纠缠的制备,操控和量度成了研究热点[5-8].对连续变量的纠缠的研究已经有较成熟的理论和一定的实验成果[9-10].腔量子电动力学(QED)的飞速发展开启了利用原子和腔耦合来制备压缩态和输出压缩(纠缠)光的研究,比如囚禁在腔中二能级原子与腔模的相互作用制备压缩态[11-12].也有单个多能级原子在大失谐的条件下与腔模相互作用制备纠缠态[13-14].众多的研究表明腔的衰变率在制备压缩(纠缠)态中有重要影响[14-18].微波场容易调控的优点被广泛运用在电磁诱导透明和纠缠等领域的研究中[19-21],微波场作用在三能级Δ型原子的2个基态间,可实现循环封闭的结构[21].另一方面,量子比特的发展为人造原子的产生奠定了基础,可采用人造原子实现封闭的Δ型原子系统[22-26].同时超导传输共振器(TLR)与传统腔相比的诸多优点也引起了广泛关注.于是人们将人造原子与超导传输共振器耦合来实现腔 QED,把这样的体系称为电路 QED体系[25-28].
本文采用的模型是将原子囚禁在腔中,该原子在微波场的作用下与腔模耦合,讨论输出场的压缩和纠缠特性.通过计算输出场的压缩(纠缠)谱,讨论了有效耦合常数、腔的衰变系数以及微波场的强度对输出场双模纠缠度的影响.最后讨论用电路QED对本文理论的实验实现.
2 物理模型
采用的三能级封闭系统如图1所示.频率为υ1和υ2的2个腔模分别与|1〉↔|2〉和|0〉↔|2〉耦合,耦合常数为g1和g2,腔模的湮灭算符为â1和â2.经典相干光场驱动场频率为ω1和ω2,Rabi频率为Ω1和Ω2,相位为φ1和φ2,分别作用到原子跃迁|0〉↔|2〉和|1〉↔|2〉上.另有微波场Ω0作用在2基态间的跃迁|0〉↔|1〉,微波场的相位为φ0,频率为ω0.光场相对于原子跃迁频率的失谐量分别为Δ1=ω12-υ1=ω02-ω1,Δ2=υ2-ω02=ω2-ω12.






3 讨论
为了研究输出场的纠缠和压缩特性,定义双模振幅正交算符的差算符和相位正交算符的和算符[11]



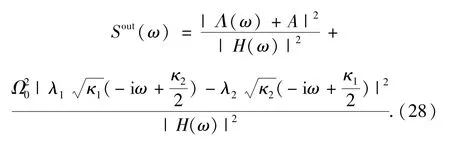


的解析式来解释.
另外,腔的衰变率会影响压缩谱(纠缠谱)的宽度,κ越大,压缩谱越宽(见图3).
如图4所示,在Ω0≠0时,最大纠缠度还是出现在中心频率ω=0处,且在腔衰变率κ和一定的情况下,Sout(0)和压缩谱宽度会随微波场的增大而逐渐减小.
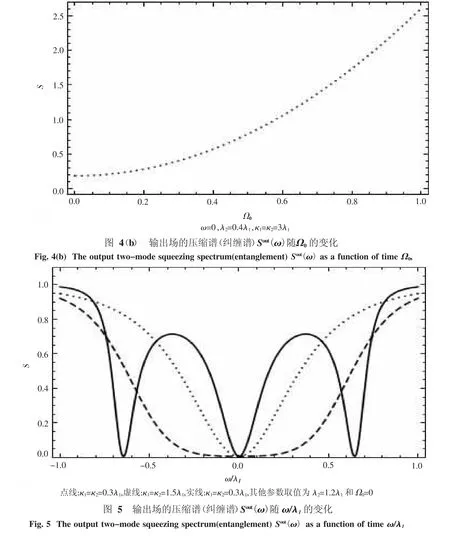
如果λ2>λ1,纠缠谱可能会出现3个极小值(见图5).当时,将出现3个极小值,且极小值出现在ω=0,处[12].如图6所示,微波场Ω0对处的纠缠度的调节作用大于对ω=0处的纠缠度的调节.从图7最大纠缠度Sout(0)随λ2/λ1的变化中不难看出,当λ2<λ1时,最大纠缠度Sout(0)随λ2/λ1的增大而增大.当λ2>λ1时,最大纠缠度Sout(0)随λ2/λ1的增大而减小.
封闭Δ型原子也可用超导磁通量量子比特来实现.用一根超导线将超导Josephson结两端连起来构成1个封闭的超导环,在这个环里加上额外的磁场φe.当时(其中,磁通量子),这个量子比特就相当于一个Λ型自然原子,基态之间跃迁是被禁止的.但是当时,这种跃迁定则被打破,任意2个态之间都能发生跃迁,这样就形成了封闭三能级系统[22-23].图1中与人造封闭三能级原子耦合的量子光场是由超导传输线共振器提供的.超导传输线共振器是将1块超导金属平板2侧分别用2块超导金属平板夹主(平板的长度远远大于宽度和平板间的间隔),而这块超导金属平板的首尾通过电容与外界电路耦合.超导传输线共振器作为一种微波腔,它具有品质高的优点,容易实现强耦合,在量子计算和量子信息方面有很重要的意义.

4 结论
本文研究了封闭三能级Δ型原子在经典相干场和微波场的驱动下与腔模的相互作用,通过绝热去掉激发态|2〉,得到有效哈密顿量.再通过输入输出理论,最终计算出输出场的压缩(纠缠)谱.我们发现输出场的压缩谱(纠缠谱)的宽度容易受腔衰变系数的影响,但可以通过调节有效耦合常数和微波场Ω0来控制.最大压缩(纠缠)度随Ω0的增大而增大.当Ω0=0时,最大压缩度与腔衰变系数无关.希望本文的研究能为量子通信提供一点理论价值.
致谢四川师范大学研究生优秀学位论文培育基金(201314)对本文给予了资助,谨致谢意.
[1]Walls D F.Squeezed states of light[J].Nature,1983,306:141-146.
[2]Braunstein S L,Kimble H J,Sorensen Y,et al.Teleportation of continuous quantum variables[J].Phys Rev Lett,1998,80:869-872.
[3]Samuel L,Braunstein,Peter V,et al.Quantum information with continuous variables[J].Rev Mod Phys,2005,77:513-577.
[4]Li W L,Li Ch F,Guo G G,et al.Probabilistic teleportation and entanglement matching[J].Phys Rev,2000,A61:034301.
[5]Piovella N,Cola M,Bonifacio R,et al.Quantum fluctuations and entanglement in the collective atomic recoil laser using a Bose-Einstein condensate[J].Phys Rev,2003,A67:013817.
[6]Gasenzer T,Roberts D C,Burnett K,et al.Limitations of entanglement between photons and atoms coupled out from a Bose-Einstein condensate[J].Phys Rev,2002,A65:021605.
[7]Peng A,Johnsson M,Bowen W P,et al.Squeezing and entanglement delay using slow light[J].Phys Rev,2005,A71:033809.
[8]Ding J L,Hou B P.Squeezing and entanglement of a two-mode field in a four-level tripod atomic system[J].Opt Commun,2011,284:2949-2954.
[9]Duan L M,Giedke G,Cirac J I,et al.Inseparability criterion for continuous variable systems[J].Phys Rev Lett,2000,84:2722-2725.
[10]Josse V,Dantan A,Bramati A,et al.Continuous variable entanglement using cold atoms[J].Phys Rev Lett,2004,92:123601.
[11]Vitali D,Morigi G,Eschner J,et al.Single cold atom as efficient stationary source of EPR-entangled light[J].Phys Rev,2006,A74:053814.
[12]Morigi G,Eschner J,Mancini S,et al.Coherent generation of EPR-entangled light pulses mediated by a single trapped atom[J].Phys Rev,2006,A73:033822.
[13]Zhou L,Xiong H,Zubairy M S,et al.Single-atom as a macroscopic entanglement source[J].Phys Rev,2006,A74:022321.
[14]Zhou L,Mu Q X,Liu Zh J,et al.Output entanglement and squeezing of two-mode fields generated by a single atom[J].Phys Lett,2009,A373:2017-2020.
[15]Mu Q X,Ma Y H,Zhou L,et al.Output squeezing and entanglement generation from a single atom with respect to a low-Qcavity[J].Phys Rev,2010,A81:024301.
[16]An J H,Feng M,Oh C H,et al.Quantum information processing with a single photon by an input-output process[J].Phys Rev,2009,A79:032303.
[17]Cheng G L,Hu X M,Zhong W X,et al.Two-channel interaction of squeeze-transformed modes with dressed atoms:Entanglement enhancement in four-wave mixing in three-level systems[J].Phys Rev,2008,A78:033811.
[18]Peng B L,Fu L L.Controlled generation of field squeezing with cold atomic clouds coupled to a superconducting transmission line resonator[J].Phys Rev,2011,A81:035802.
[19]Scully M O,Zubairy M S.Quantum Optics[M].London:Cambridge University Press,1997.
[20]Bortman-Arbiv D,Wilson-Gordon A D,Friedmann H,et al.Phase control of group velocity:from subluminal to superluminal light propagation[J].Phys Rev,2001,A63:043818.
[21]Wilson E A,Manson N B,Wei C,et al.Perturbing an electromagnetically induced transparency in a system using a low-frequency driving field I three-level system[J].Phys Rev,2005,A72:063813.
[22]Liu Y X,You J Q,Wei L F,et al.Optical selection rules and phase-dependent adiabatic state control in a superconducting quantum circuit[J].Phys Rev Lett,2005,95:087001.
[23]Jia W Z,Wei L F.Gains without inversion in quantum systems with broken parities[J].Phys Rev,2010,A82:013808.
[24]You J Q,Nori F.Atomic physics and quantum optics using superconducting circuits[J].Nature,2011,474:589.
[25]Li P B,Li F L.Engineering squeezed states of microwave radiation with circuit quantum electrodynamics[J].Phys Rev,2011,A83:035807.
[26]Chen Y L,Xiao Y F,Zhou X X,et al.Single-photon transport in a transmission line resonator interacting with two capacitively coupled Cooper-pair boxes[J].J Phys B:Atom,Mol Opti Phys,2008,B41:175503.
[27]Manucharyan,Koch J,Glazman L I,et al.Fluxonium:single cooper-pair circuit free of charge offsets[J].Science,2009,326:113-116.
[28]Hu Y,Ge G Q,Chen S,et al.Cross-Kerr-effect induced by coupled Josephson qubits in circuit quantum electrodynamics[J].Phys Rev,2011,A84:012329.
[29]Hou B P,Wang S J,Yu W L,et al.Control of one-and two-photon absorption in a four-level atomic system by changing the amplitude and phase of a driving microwave field[J].J Phys,2005,B38:1419-1434.
[30]Daniel F V J,Jonathan J.Effective hamiltonian theory and its applications in quant um information[J].Phys,2000,48:823.
[31]胡小会,侯邦品.五能级原子系统中的双光子双重电磁诱导透明[J].四川师范大学学报:自然科学版,2009,32(2):191-194.
[32]侯邦品.K-型五能级原子的双重单光子电磁诱导透明[J].四川师范大学学报:自然科学版,2007,30(6):740-743.
[33]蓝海江,侯邦品.增、减光子压缩真空态的维格纳函数及其非经典特性[J].四川师范大学学报:自然科学版,2011,34(1):80.
[34]王婷,侯邦品.五能级M型原子双重通道的量子信息存储和释放[J].四川师范大学学报:自然科学版,2013,36(3):409-412.
[35]郭俊杰,谢征微.原子-分子玻色-爱因斯坦凝聚系统中Q函数和量子动力学研究[J].四川师范大学学报:自然科学版,2011,34(3):340-344.
