环境一号C星构架反射器展开驱动部件优化设计

黄志荣 郑士昆 朱佳龙 陈国定

①(中国空间技术研究院西安分院 西安 710100)

②(西北工业大学机电学院 西安 710072)

1 引言

环境一号 C星构架式反射器展开驱动部件采用弹簧为动力源，弹簧零件的可靠性直接影响到反射器的展开和工作性能。根据驱动部件失效模式及其影响分析(FMEA)及实际工程应用情况分析可知，弹簧零件的应力松弛和冲击破坏是导致驱动失效的主要形式，它们分别会引起展开扭矩、保持裕度下降和展开性能破坏等故障，甚至直接导致反射器展开失败。因此，针对主要失效形式，对展开驱动部件关键弹簧零件的优化设计具有重要的工程实践意义。

文献[1-3]探讨了拉压弹簧及某些弹簧材料在特定条件下的应力松弛规律；文献[4-6]进行了拉压弹簧和扭杆弹簧在冲击载荷下的动态响应仿真及实验研究；文献[7]基于静破坏和疲劳破坏两种失效形式，进行了以刚度误差最小和质量最小为目标的螺旋弹簧优化设计；文献[8]则基于疲劳破坏进行了拉压弹簧的可靠性优化；文献[9]基于多种失效模式，应用广义应力-广义强度分布干涉理论，开展了扭簧的可靠性优化分析。综上所述，大多研究集中于拉压弹簧的特性分析及扭簧的优化设计，而环境一号C星构架反射器驱动部件中所使用的弹簧为扭簧和涡卷弹簧，由于不同种类弹簧特性差异极大，故面向项目实际应用，开展驱动部件弹簧(扭簧和涡卷弹簧)的优化设计非常必要。

本文基于构架反射器展开驱动部件FEMA，获得弹簧优化设计需要着重考虑的失效形式；针对疲劳松弛及冲击破坏的两类失效形式，分别对项目需要的扭簧和涡卷弹簧进行了基于可靠性的优化设计，并通过优化前后弹簧的可靠性比较，验证了优化的有效性。

2 结构及失效形式

2.1 展开驱动部件结构

环境一号 C星构架反射器桁架结构如图 1所示，由若干个构架式单元拼接组成；每个单元为图2所示的四面体结构，由3根腹杆、3根同步折叠杆、4个花盘节点和3个同步铰链等组件构成。其中，花盘节点组件通过销轴和扭簧与杆件联接，同步铰链组件通过涡卷弹簧和销轴联接同步杆，共同构成展开驱动部件。天线预先进行折叠收拢并锁紧，展开驱动部件中的弹性零件积聚弹性势能；入轨后反射器桁架在弹性零件驱动下实现展开。

2.2 驱动部件FMEA分析

根据反射器桁架结构及实际工作情况，可以获取展开驱动部件的FMEA分析表，其结果表明弹簧的失效构成了部件的主要失效形式，且其相应风险顺序位于前列。归纳扭簧和涡卷弹簧的主要失效形式分别为：扭簧应力松弛、扭簧冲击破坏、扭簧静破坏、扭簧疲劳破坏等。对失效形式进行重要度评估可知，两种弹簧的应力松弛和冲击破坏是最重要的两类故障形式，故下面基于弹簧进行展开驱动部件的优化设计，以提高其可靠度；优化设计对象为同步杆与花盘联接的扭簧和同步铰链组件内的涡卷弹簧。

3 扭簧优化设计

3.1 基于应力松弛失效的原型扭簧可靠性分析

(1) 扭矩松弛计算

通过展开驱动部件原型扭簧的应力松弛测试试验，可获得扭簧承受某扭矩一段时间后，若干时间节点扭簧的残余扭矩数据，并可计算得到相应的扭矩衰减量(表 1所示为原型扭簧的扭矩衰减量)。根据试验数据，拟合出扭矩衰减与时间的关系曲线表达式如式(1)所示，它表征了扭簧的扭矩衰减规律。

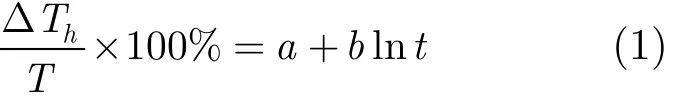
式中，ΔTh是经过h小时应力松弛后扭矩的衰减量；常数a为扭簧保持1 h的扭矩衰减率；常数b为扭矩衰减率变化速率。

(2) 可靠度计算

基于式(1)可计算出扭簧收拢扭矩及若干小时后扭簧松弛的残余扭矩。分析其分布特性，并根据广义应力-广义强度的概念[10]，可获得基于应力松弛的扭簧可靠度R，表示为：

式中，Thmax为h小时后扭簧的残余扭矩，Tcmax为扭簧临界收拢扭矩。

由式(2)计算出基于应力松弛的扭簧可靠度如表1所示。

图1 构架天线展开结构示意图Fig.1 Schematic diagram of antenna deployable structure

表1 原型扭簧基于应力松弛失效的可靠度Tab.1 Reliability of prototype torsion spring on stress relaxation failure

3.2 基于冲击破坏的原型扭簧可靠度分析

首先进行扭簧冲击特性分析，根据原型扭簧冲击试验，可获得不同扭转角度、负载转动惯量和冲击次数下扭簧的冲击扭矩数据，通过分析其相对于初始静扭矩的放大倍数，可获得冲击扭矩特性规律。其次，与上节类似，由冲击扭矩规律获得其分布特性，依据广义力-广义强度干涉理论可获得原型扭簧基于冲击破坏的可靠度为：

3.3 优化设计

扭簧的优化须在保证扭簧与展开驱动部件及桁架其他零件结构关系不变的情况下进行。可行的可靠性增长方式包括提高扭簧制造精度，提高扭簧钢丝材料的强度等级，以及改变扭簧尺寸等。由于部件的制造精度已经较高，所以项目主要从后两种途径进行可靠性优化设计分析，使扭簧在面对冲击具备较高可靠性的同时，能够提高面向应力松弛失效的可靠性。

分别加工一系列材料、扭簧旋绕比、扭簧工作圈数等参数不同的改进型扭簧试件，进行应力松弛测试试验，根据所测试试验数据分别计算基于应力松弛失效的扭簧衰减扭矩和可靠度，如表2所示。

对比表1和表2数据，可获得各参数对扭簧基于应力松弛失效可靠性的影响规律：在尺寸参数一致的情况下，相比原型不锈钢丝扭簧，选用强度等级更高的琴钢丝材料制成的改进型扭簧，可靠性并无提升；在相同材料情况下，提高扭簧旋绕比和工作圈数都可以提高扭簧的可靠度，但工作圈数的改变对扭簧基于应力松弛失效的可靠度影响更为显著。

根据50 h松弛后可靠度大于0.93的使用要求，可选用Ⅱ,Ⅲ,Ⅳ型扭簧。但综合考虑扭簧的扭矩衰减发现，满足50 h后扭簧衰减量小于1.5 N⋅ mm的仅有Ⅲ型扭簧，故确定该改进型扭簧为最终优化结果。对比优化前后的扭簧特性，图3所示为原型扭簧和优化后扭簧基于应力松弛失效形式的扭簧衰减扭矩曲线；图4所示为原型扭簧和优化后扭簧基于冲击破坏失效形式下，扭簧冲击应力的统计分布；表3所示为优化后扭簧基于应力松弛和冲击破坏失效的可靠度。

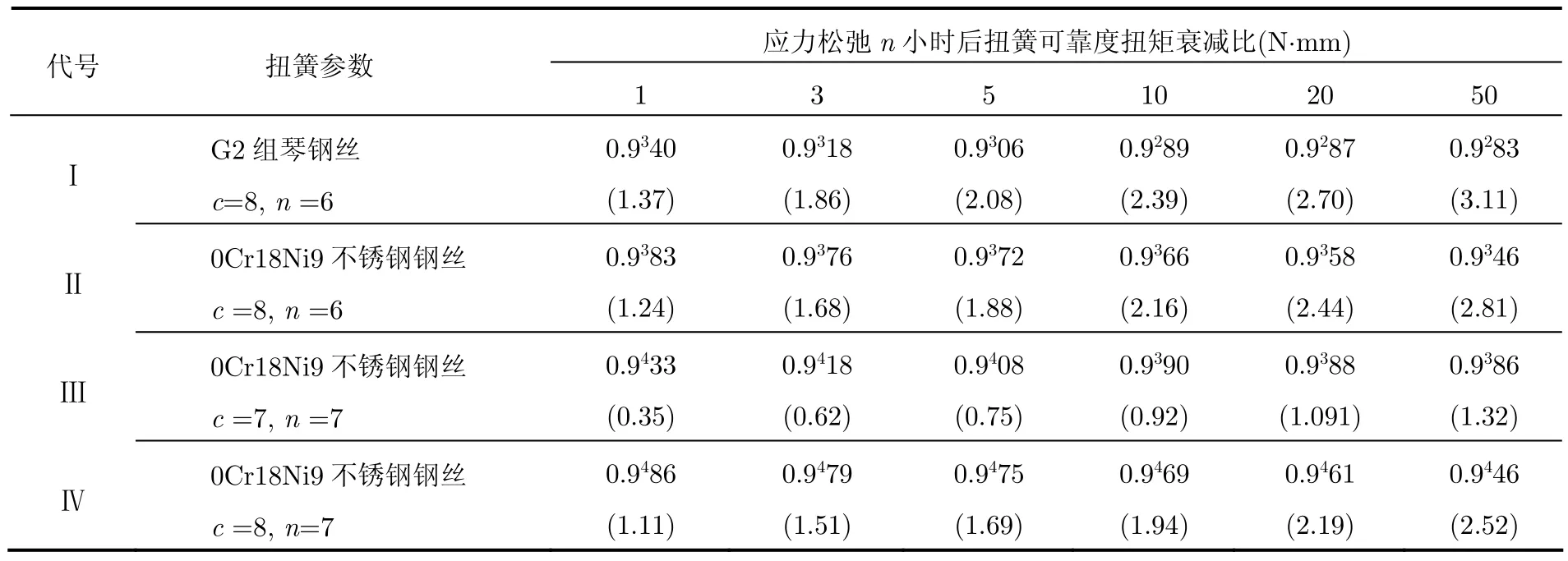
表2 改进型扭簧试件基于应力松弛失效的可靠性分析数据Tab.2 Reliability analysis data of improved torsion spring specimen on stress relaxation failure

图3 扭簧优化前后的应力松弛扭矩衰减对比Fig.3 Comparison of spring stress relaxed damping torque before and after optimization

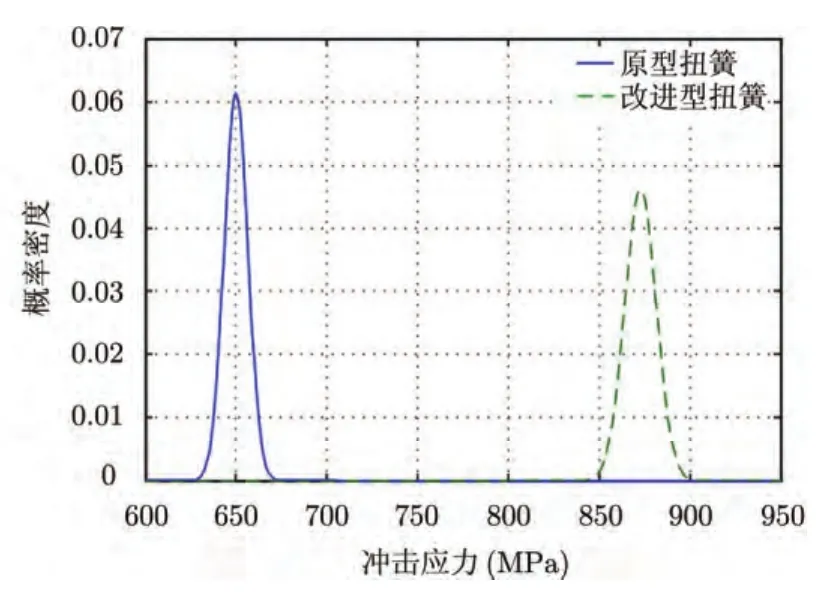
图4 扭簧优化前后冲击应力分布比较Fig.4 Comparison of spring impact stress distribution before and after optimization

表3 优化后扭簧的可靠度Tab.3 Reliability of optimized torsion spring

综合对比表1，表3及图3，图4可见，优化后扭簧应对应力松弛失效的扭矩衰减明显下降，基于应力松弛失效的扭簧可靠度有显著提高；针对冲击破坏失效，优化后冲击应力增加，但基于冲击破坏失效的扭簧仍具有较高的可靠度；说明优化有效可行。

4 涡卷弹簧优化设计

4.1 原型涡簧可靠性分析

原型涡簧可靠度同样基于应力松弛和冲击破坏两种失效形式分别分析，通过类似原型扭簧的方法，可计算得到两种失效形势下的涡簧可靠度，分别如表4所示。

4.2 优化设计

涡簧的优化可采用提高制造精度、材料强度等级及改变尺寸的方式实现，但由于原型涡簧的加工精度和材料机械性能已较高，故仅考虑通过增大涡簧钢带厚度和宽度等尺寸参数的途径来进行涡簧可靠度优化，使涡簧在面对应力松弛失效具备较高可靠性的同时，能够提高其面对冲击的可靠性。

根据涡簧测试可获得涡簧性能与尺寸参数的约束关系，分别加工一系列改进型涡簧试件，进行基于冲击破坏失效的可靠性测试，数据如表5所示。

由表5可见，相比原型涡卷弹簧，增加钢带宽度和钢带厚度都可有效降低涡卷弹簧的冲击应力，显著提高可靠性。但考虑到安装尺寸的限制，选用Ⅱ型涡卷弹簧为最终优化结果。对比优化前后涡簧特性可得，如图5所示为原型涡簧和优化后涡簧基于应力松弛失效形式的扭矩衰减曲线；图6所示为原型涡簧和优化后涡簧基于冲击破坏失效形式的涡簧冲击应力统计分布；表6所示为优化后涡簧基于应力松弛和冲击破坏失效的可靠度。

综合表4，表6及图5，图6可知，优化后涡簧应对应力松弛失效的扭矩衰减略有增大，但基于应力松弛失效仍具有较高的可靠度；针对冲击破坏失效，优化后涡簧冲击应力显著下降，且对应可靠度有明显提升；说明涡簧优化是有效的。

表4 原型涡卷弹簧的可靠度Tab.4 Reliability of prototype scroll spring

表5 涡卷弹簧试件基于冲击破坏失效的可靠性分析数据Tab.5 Reliability analysis data of scroll spring specimen on Impact breakage failure

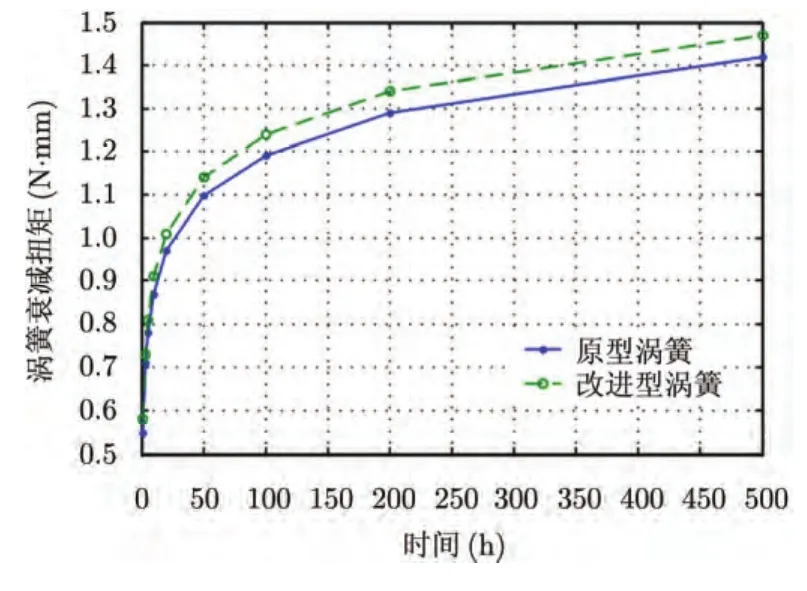
图5 涡簧优化前后的松弛衰减扭矩对比Fig.5 Comparison of scroll spring relaxed damping torque before and after optimization

图6 涡簧优化前后冲击应力分布比较Fig.6 Comparison of scroll spring impact stress distribution before and after optimization

表6 优化后涡卷弹簧的可靠度Tab.6 Reliability of improved scroll spring

5 结论

本文针对环境一号 C星构架式反射器展开驱动部件易出现疲劳、破坏等问题，提出驱动部件扭簧和涡卷弹簧的优化措施，开展了基于可靠度的优化设计。测试分析表明，优化方案有效可靠，优化后的构架反射器系统可靠度大幅提升。该优化设计结果已应用到环境一号C星型号工程研制中，为天线在轨成功展开奠定了基础。此外，本文提及的弹性部件可靠性优化设计方法还可直接应用于其他天线。

[1]常新龙,刘兵吉,汪亮.螺旋弹簧应力松弛实验研究[J].推进技术,1999,20(1): 99-102.Chang Xin-long,Liu Bing-ji,and Wang Liang.Experimental study on stress relaxation of helical spring[J].Journal of Propulsion Technology,1999,20(1): 99-102.

[2]魏芳荣,李家俊,李群英,等.螺旋压缩弹簧应力松弛性能的动态试验研究[J].金属热处理,2007,32(4): 47-50.Wei Fang-rong,Li Jia-jun,Li Qun-ying,et al..Dynamic experiment on stress relaxation properties of helical compress spring[J].Heat Treatment of Metals,2007,32(4): 47-50.

[3]李建明,赵乃勤,李群英,等.65Mn弹簧钢在弯曲应力下的松弛行为[J].金属热处理,2007,32(5): 90-94.Li Jian-ming,Zhao Nai-qin,Li Qun-ying,et al..Bending stress relaxation behavior of 65Mn spring steel[J].Heat Treatment of Metals,2007,32(5): 90-94.

[4]符朝兴,王秀伦.扭杆弹簧受短波冲击的响应研究[J].机械设计与制造,2006,(1): 29-31.Fu Zhao-xing and Wang Xiu-lun.Response research of helical spring impacted by short wave[J].Machinery Design &Manufacture,2006,(1): 29-31.

[5]Pastorelli S,Almondo A,and Sorli M.Effects of mechanical and pneumatic return springs on valve train dynamics[C].Proceedings of ESDA20068th Biennial ASME Conference on Engineering Systems Design and Analysis,Torino,Italy,2006:263-271.

[6]Jeong-hyun Sohn,Seung-kyu Lee,Seung-oh Kim,et al..Comparison of spring models for dynamics simulation of spring operating mechanism for circuit breaker[C].Proceedings of the ASME 2007 International Design Engineering Technical Conferences & Computers and Information in Engineering Conference IDETC/CIE 2007,Las Vegas,Nevada,USA,2007: 1017-1023.

[7]刘文清.螺旋弹簧可靠性多目标优化设计[J].山西机械,2001,3(1): 16-20.Liu Wen-qing.The reliability multi-target optimization design of helical spring[J].Shanxi Machinery,2001,3(1): 16-20.

[8]魏宗平.基于可靠性约束的变载荷圆柱螺旋压缩弹簧的优化设计[J].机械设计与制造,2006,(5): 28-30.Wei Zong-ping.Optimization design based on reliability for variable load cylinder helix compression spring[J].Machinery Design & Manufacture,2006,(5): 28-30.

[9]王梅,陈国定,肖勇.基于多失效模式的扭簧可靠性优化分析[J].中国空间科学技术,2011,10(5): 57-63.Wang Mei,Chen Guo-ding,and Xiao Yong.Optimal analysis of the reliability for torsion spring based on multi-failure modes[J].Chinese Space Science and Technology,2011,10(5):57-63.

[10]刘惟信.机械可靠性设计[M].北京: 清华大学出版社,1996:151-187.Liu Wei-xing.Mechanical Reliability Design[M].Beijing:Tsinghua University Press,1996: 151-187.