3DR39-3d方位关系模型与反方位关系

郝晓红，张丽平，赵龄强，李 松

(哈尔滨理工大学计算机科学与技术学院，哈尔滨 150080)

1 概述

作为空间关系的3大关系之一，空间方向关系在空间数据库、地理信息系统、空间数据挖掘、空间数据查询、机器人智能等领域具有重要的作用[1]。

目前，国内外对空间方向关系的研究主要集中在2条主线上[1]：2D空间中的方向关系表示和推理技术与3D空间中的方向关系表示和推理技术。2D空间中方向关系的表示模型已经较为丰富，研究成果主要有投影模型、锥形模型、四半区域模型、最小外接矩形模型、2D-String关系模型和2D不确定方向关系模型等。近年在基于MBR模型的2D主方向关系的表示和推理，以及路径一致性检验[2]和方向关系的组合表示与分析[3-4]等领域也取得了重要的成果。对于3D空间中的方向关系，由于3D空间对象的复杂性和多样性使得3D空间中方向关系的表示和分析技术更有难度。3D方向关系的研究主要集中在3D方向关系模型的建立、3D方向关系推理和3D方向关系查询等方面。文献[5]将二维双十字模型扩展到3D空间，以描述3D空间点对象间的方向关系，但该方法将空间对象全部抽象为点，忽略了空间对象的形状与大小，在实际应用中具有很大的局限性。文献[6]将2D主方向关系拓展到3D空间，建立了一种新的3D方向关系模型。基于所建立的模型进一步研究了组合关系、反向关系和一致性检验等重要内容。文献[7]扩展了2D空间中开放区域模型的抽象基类，基于对象方位的2D方向关系描述模型提出了3D空间中的开放区域模型。文献[8]基于对象相交立方体矩阵来描述3D空间中的主方向关系。文献[9]基于3DR7模型、3DR27模型和3DR39模型给出3D空间体对象的单方向动态邻接关系表，基于3DR27模型给出方向关系的双向映射模型。文献[10]对3D空间中的3DR44模型进行了详细研究。但上述模型仅对3D空间进行方向划分，只能对复杂的3D空间对象进行方向关系的描述，无法对3D空间距离关系进行表示。已有模型在表示和区分3D方向关系相同，但位置关系具有很大差别的空间方位关系方面具有较大的局限性。模型表示精度在实际应用中有时不理想。

3DR39方向关系模型的空间划分较为合理简明且可扩充性较高，该模型具有较大的应用价值，但单纯利用单一的3DR39方向关系模型具有较大的局限性。为了弥补已有方法和模型的不足，本文将3DR39方向关系和距离位置关系相结合，提出一种新的3D空间关系模型，即3DR39-3d方位关系模型，简称3DR39-3d模型。3DR39-3d模型将方向关系和距离位置关系进行较好的融合，能定性反映3D空间中大量具有方向和位置双重属性的复杂的空间关系，即3D方位关系，可表示和区分2115种复杂的3D方位关系。

2 3DR39-3d方位关系模型

由于3DR39方向关系模型[9]仅考虑了TO(目标对象)与NO(参照对象)之间的定性方向关系，没有涉及定性的距离关系，因此单纯利用3DR39方向关系模型无法进一步处理具有距离关系的复杂空间方位关系的表示和区分问题。例如，图1中目标对象TO1和TO2相对于参照对象NO的方向关系在3DR39模型中是一样的，即3DR39模型无法对其进一步区分，但TO1和TO2实际上相对于参照对象NO的空间关系具有较大的位置差异。

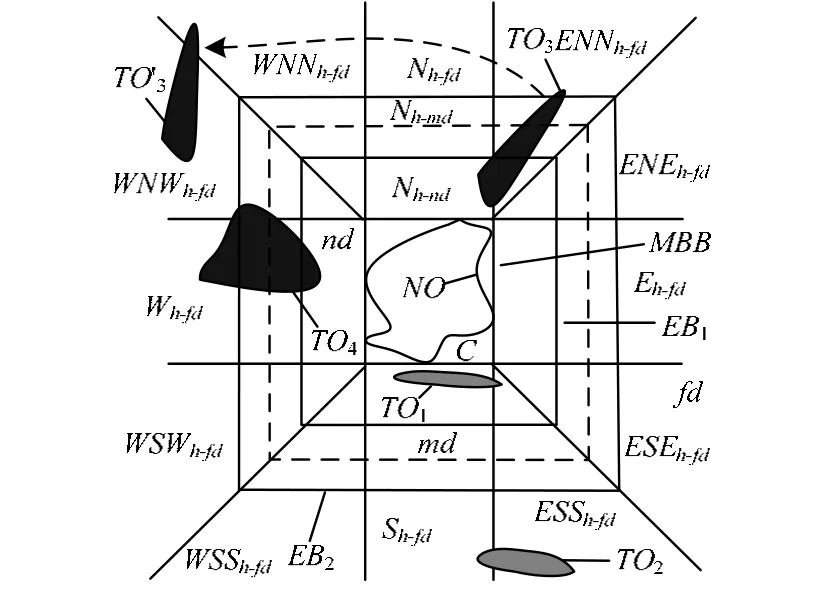
图1 3DR39-3d方位关系模型平面投影

为了进一步提升计算机对复杂空间方位关系的表示和区分能力，本节给出3DR39-3d方位关系模型。

定义1(盒空间)在三维立体空间中，参照对象NO的最小包围盒(MBB)称为NO的本体盒，将本体盒向各个方向进行均匀扩展而得出不同体积的扩充盒，记为EB。扩充盒的各个面将3D空间分割划成距离NO远近不同的子空间，将这些的子空间统称为盒空间。

扩展盒的数量不同，划分的子空间数相应的也不同，本文着重研究基于2个扩展盒划分成的3个盒空间与3DR39方向关系模型的组合表示与动态分析问题。如图1所示，NO的扩展盒EB1和EB2将3D空间分成nd,md和fd共3个子空间，nd,md和fd分别定性表示距离NO的近距离空间，较近距离空间和较远距离空间。其中，nd和md是封闭的3D距离空间；fd是半封闭的三维距离空间。

定义2(3d距离关系)设G={nd,md,fd}表示包含3个盒空间的定性距离关系符号集，设2G表示集合G的幂集，则三维空间对象TO(目标对象)与NO(参照对象)的距离关系可表示为二元函数3d(NO,TO),3d(NO,TO)∈2G。简称为3d距离关系。

由于nd,md和fd是定性划分的距离空间，因此根据实际需要，nd,md和fd可动态地进行调整(扩展或缩小)。例如，EB2不变，EB1扩展到图1中的虚线所示时，则nd相应的扩大，md缩小，fd保持不变。TO相对于NO的定性的3d距离关系描述相应会受到影响。

将3d距离关系结合进3DR39方向关系模型，则进一步可得出能更为精细表示定性距离和方向关系的3DR39-3d方位关系模型，如定义3所示。

定义3(3DR39-3d模型的方位关系)设距离关系元素集G={nd,md,fd},g∈G,H={u,d,m},h∈H,DR为3DR39方向关系模型的方向空间元素集。令gDR={Ed-g,ESEd-g,ESSd-g,Sd-g,WSd-g,WSWd-g,Wd-g,WNWd-g,WNNd-g,Nd-g,ENNd-g,ENEd-g,Em-g,ESEm-g,ESSm-g,Sm-g,WSSm-g,WSWm-g,Wm-g,WNWm-g,WNNm-g,Nm-g,ENNm-g,ENEm-g,Eu-g,ESEu-g,ESSu-g,Su-g,WSSu-g,WSWu-g,Wu-g,WNWu-g,WNNu-g,Nu-g,ENNu-g,ENEu-g,Cu-g,Cu-g,Cm-nd}，设2gDR表示gDR的幂集，则三维空间对象TO(目标对象)与NO(参照对象)的方位关系可表示为二元函数3DIR39-3d(NO,TO),3DIR39-3d(NO,TO)∈2gDR。图1展示了3DR39-3d方位关系的平面投影。

在定义3中，gDR中的各项表示基于3d距离关系结合进3DR39方向关系模型划分的更细方位空间元素。每个方位空间元素由距离关系集{nd,md,fd}和层标识集{u,d,m}联合表示。例如，在图1中，Nh-md即表示Nd-md,Nu-md,Nm-md这3个方位空间元素的平面投影。3D439-3d方位关系模型将3D空间划分为3层，本文用u,d,m表示，每层包含大量的方位空间元素，每个空间元素的距离信息由nd,md,fd来表示。例如，WSWu-md，即表示第u层，定性距离为md的3D空间方位元素WSW。

基于定义3，可给出三维空间对象TO(目标对象)与NO(参照对象)的方位关系交集序列：T1={Ed-g∩NO,ESEd-g∩NO,ESSd-g∩NO,Sd-g∩NO,WSd-g∩NO,WSWd-g∩NO,Wd-g∩NO,WNWd-g∩NO,WNNd-g∩NO,Nd-g∩NO,ENNd-g∩NO,ENEd-g∩NO,Em-g∩NO,ESEm-g∩NO,ESSm-g∩NO,Sm-g∩NO,WSSm-g∩NO,WSWm-g∩NO,Wm-g∩NO,WNWm-g∩NO,WNNm-g∩NO,Nm-g∩NO,ENNm-g∩NO,ENEm-g∩NO,Eu-g∩NO,ESEu-g∩NO,ESSu-g∩NO,Su-g∩NO∩NO,WSSu-g∩NO,WSWu-g∩NO,Wu-g∩NO,WNWu-g∩NO,WNNu-g∩NO,Nu-g∩NO,ENNu-g∩NO,ENEu-g∩NO,Cu-g∩NO,Cu-g∩NO,Cm-nd∩NO}。

由G={nd,md,fd},g∈G可知，将g由nd,md和fd代换，T1可进一步展开描述。由T1的定义可知，T1交集序列共含有115个交集项，其0,1串所能表达的3D空间中的方位关系将高达2115种，进一步增强了方位关系的表示精度。

3 3DR39-3d模型的动态方位关系

目标对象TO相对于参照对象NO的方位关系往往不是静止不变的，TO和NO的运动均能导致方位关系发生变化。探讨方位关系的动态变化规律具有重要意义。本节对基于对象运动的动态方位关系和基于盒空间扩张的动态方位关系进行了研究。

3.1 基于对象运动的动态方位关系

目标对象或参照对象的位置随时间往往会发生动态的变化，例如，在图1中，目标对象TO3由t1时刻到t2时刻运动到TO′3，在t1时刻，TO3所处的方位空间元素集FE1为{ENNu-fd,ENNu-md,ENNu-nd,ENNm-fd,ENNm-md,ENNm-nd,ENNd-fd,ENNd-md,ENNd-nd,Nu-fd,Nm-md,Nd-nd}；在t2时刻，目标对象所处的方位空间元素集FE2为{WNNu-fd,WNNm-fd,WNNd-fd,WNWu-fd,WNWm-fd,WNWd-fd}。t1时刻到t2时刻，TO3相对于NO的方位关系发生了较为显著的变化，其经历的中间方位关系则更为复杂、多样。由于较为复杂的空间方位关系均可分解成目标对象相对于参照对象的各个方位空间元素的空间关系，方位关系的变化即是所处的相关方位空间元素的动态改变。方位空间元素的动态改变进一步可分解为一系列方位空间元素的动态邻接关系的变化。

在本文中，某方位关系的下一邻接方位关系定义为该空间方位关系由一个状态不经过中间方位关系直接转变为的空间方位关系。利用枚举和逐一排除法，本节给出3DR39-3d模型的部分方位空间元素的动态邻接关系，如表1所示。表1展示了3DR39-3d模型中的m层方位空间元素的动态邻接关系。根据3DR39-3d模型的动态邻接关系，进一步可对复杂对象的动态方位关系变化情况进行分析、预测、排错和择优。例如，沿图1的曲线运动，若根据数据信息所得出TO3在t1时刻的下一紧邻时刻t′1所处的动态邻接方位空间元素集FE3为{Nu-fd,Nu-md,Nu-nd,Nm-fd,Nm-md,Nm-nd,Nd-fd,Nd-md,Nd-nd}。则由动态邻接方位关系表(表1)对其进行检测分析可知，TO3在t1时刻所处的方位空间元素集FE1在下一紧邻时刻不能直接转变为FE3，直接转变成的方位空间元素集应为{ENNu-fd,ENNu-md,ENNu-nd,ENNm-fd,ENNm-md,ENNm-nd,ENNd-fd,ENNd-md,ENNd-nd,Nu-nd,Nm-nd,Nd-nd,Nu-md,Nm-md,Nd-md}。从而说明FE3有误，需重新收集方位信息进行分析。

表1 3DR39-3d模型的部分方位动态邻接关系

3.2 基于盒空间扩张的动态方向关系

在实际应用中，nd,md和fd等 3个定性距离空间经常会进行定性调整，即盒空间大小会发生动态的变化(扩张或缩小)。盒空间的变化将会导致部分相关的方位空间元素集相应发生动态改变。从而，将会对目标对象TO相对于参照对象NO的空间方位关系产生动态的实质性影响。

在3DR39-3d模型中，nd,md和fd的变化是由扩展盒EB1和EB2的变化决定的。EB1和EB2变化分为(EB1扩张，EB2扩张)，(EB1扩张，EB2缩小)，(EB1扩张，EB2恒定)，(EB1缩小，EB2扩张)，(EB1缩小，EB2缩小)，(EB1缩小，EB2恒定)共6种情况。每种情况都会引起部分方位空间元素发生相应的变化。基于3DR39-3d模型方位空间的划分和分布，表2给出了(EB1扩张，EB2不变)所引起的方位空间元素变化和动态迁移规律。其他情况的方位空间元素的动态变化规律可类似得出。表2中的“↓”表示相应的方位空间元素变小，“↑”表示相应的方位空间元素变大；“→”表示方位空间动态迁移。

表2 方位空间元素的变化和动态迁移

4 3DR39-3d模型的反方位关系

现实中，由于应用的需求，空间参照对象NO和空间目标对象TO的角色往往会经常变换。即确定TO相对于NO的空间方位关系的问题和确定NO相对于TO的空间方位关系的问题均有可能出现。如图2所示，NO2,NO3,NO4相对与NO1具有各自的空间方位关系，相反，NO1相对于NO2,NO3,NO4也具有不同的空间方位关系。

图2 3DR39-3d反关系模型平面投影示例

基于定义3，在3DR39-3d方位关系模型中，将方位关系3DR39-3d(TO,NO)称为3DR39-3d(NO,TO)的反方位关系，简称反关系。若基于每个空间对象均建立3DR39-3d模型，进而对其进行方位关系的表示和确定，则在空间对象数量较少时效率较高，在需要确定大量的空间对象间的方位关系及其反关系时，计算量将显著增大。由于复杂的空间方位关系的反关系可分解为基本方位空间元素的反关系，因此表3进一步给出了3DR39-3d模型的基本方位空间元素的反关系。利用基本方位空间元素的反关系的组合即可在不需要对每个空间对象都建立3DR39-3d模型的情况下推理得出复杂的空间方位关系的反关系。

表3 部分3DR39-3d模型基本方位空间元素的反关系

5 模型比较与实验分析

本节从关系模型及处理方法的表示能力、静态和动态的针对性，反关系推导能力等方面和已有研究成果进行了对比。比较结果如表4所示。方法1～方法6分别表示文献[5]～文献[10]采用的方法。“√”表示相应方法适用；“×”表示不适用。本文基于3DR39方向关系和3d距离关系的结合所提出的3DR39-3d模型可表示和区分2115种复杂的方向关系，较已有的方法具有更强的表示能力。进一步的，和其他研究成果相比，本文方法更适合处理3D动态方向关系，且对3D方位关系的反关系推导具有较强的处理能力。

表4 典型方法比较

为了分析本文所研究方法的效率，在Pentium 4,3.2 GB CPU，4 GB内存，Windows XP环境下，利用C++builder 6.0进行了实验比较分析。图3给出了利用动态方位邻接关系进行方位关系判断排错的实验结果。其中，横坐标表示动态方位空间元素集的个数，纵坐标表示利用本文所研究的动态方位邻接关系进行计算推导的效率和对每个动态方位空间元素集中的每个空间方位元素进行逐一计算的效率之比。由图3可知，当动态方位空间元素集的数目较少时，2种方法的效率差别不大，但当元素集数目逐渐增多时，利用动态方位邻接关系进行方位关系的判断排错具有更为显著的计算优势。

图3 动态方位关系计算效率

图4给出了方位关系的反关系计算效率比较结果。其中，横坐标表示由目标对象变换为参照对象的空间对象个数，纵坐标表示利用本文所提出的基本方位空间元素的反关系进行计算推导的效率和对每个空间对象都建立3DR39-3d模型进行计算的效率之比。

图4 方位空间关系的反关系计算效率

由图4可知，在所转变角色的空间对象个数较少时，2种方法计算反关系的效率差异较小；但当空间对象的个数较多时，利用基本方位空间元素的反关系的组合推理计算复杂的空间方位关系的反关系效率较高。

6 结束语

本文将3DR39方向关系模型和3d距离关系模型结合，提出了3DR39-3d方位关系模型，增强了三维方位关系的表示精度；详细研究了3DR39-3d方位关系模型的动态方位关系的表示和分析方法；给出了3DR39-3d模型的基本方位空间元素的反关系。利用基本方位空间元素的反关系组合即可在不需要对每个空间对象都建立3DR39-3d模型的情况下推理得出复杂空间方位关系的反关系。本文的研究成果作为基础理论框架模型的一部分，已应用于所开发的空间关系模拟分析软件SR-3中。下一步研究重点主要是将Vague区域关系[11-12]进行扩展，结合3DR39-3d方位关系模型以处理复杂的不确定3D空间方位关系问题。

[1]李 松,张丽平.空间关系查询与分析[M].哈尔滨:哈尔滨工业大学出版社,2011.

[2]Cicerone S,Felice P D.Cardinal Directions Between Spatial Objects:The Pairwise Consistency Problem[J].Informatics and Sciences,2004,164(1/4):165-188.

[3]Skiadopoulos S,Koubarakis M.Composing Cardinal Direction Relations[J].Artificial Intelligence,2004,152(2):143-171.

[4]Schockaert S,de Cock M,Kerre E E.Modelling Nearness and Cardinal Directions Between Fuzzy Regions[C]//Proc.of IEEE World Congress on Computational Intelligence.[S.l.]:IEEE Press,2008:1548-1555.

[5]Pacheco J,Escrig M T,Toledo F.Integrating 3D Orientation Models[C]//Proc.of the5th Catalonian Conference on Artificial Intelligence.Castellon,Spain:[s.n.],2002:88-100.

[6]Chen Juan,Liu Dayou,Jia Haiyang,et al.Cardinal Direction Relations in 3D Space[C]//Proc.of the 2nd International Conference on Knowledge Science,Engineering and Management.Melbourne,Australia:[s.n.],2007:623-629.

[7]Liu Yongshan,Gao Shiwei,Wang Dechen,et al.Open Shape Model Based on Absolute Frame in Three-dimensional Space[J].Innovative Computing,Information and Control Express Letters,2009,3(3(B)):599-605.

[8]Chen Tao,Schneider M.Modeling Cardinal Directions in the 3D Space with the Objects Interaction Cube Matrix[C]//Proc.of ACM Symposium on Applied Computing.New York,USA:[s.n.],2010:906-910.

[9]张丽平,李 松.3D对象动态方位邻接关系及双向关联表示[J].计算机工程与应用,2009,45(29):68-71.

[10]郝晓红,张丽平,李 松.三维空间中3DRR44方向关系表示模型[J].计算机工程,2011,37(1):75-77.

[11]李 松,郝忠孝.基于Vague集的含洞不规则Vague区域关系[J].计算机研究与发展,2009,46(5):823-831.

[12]张丽平,李 松,郝晓红,等.Jrv粗糙Vague区域关系[J].浙江大学学报:工学版,2012,46(1):105-111.