社交网络中一种基于模块化的社区检测算法
2014-09-29崔泓
崔 泓
(渤海大学计算机教研部,辽宁 锦州 121013)
1 概述
许多社交网络都具有社交结构这一属性[1],假设顶点表示网络用户,连接线(链接)表示用户的社交互动行为,则社交网络可以很自然地分为多组顶点和少量连接线,其中,各组顶点的内部连接线非常密集,而各组间的连接线较少。各社交网络社区的成员往往具有许多共性,如均对摄影、电影、音乐或其他讨论主题感兴趣;因此,他们彼此之间的交流频率要比与社区之外成员的交流频率高。检测网络社区可以提供关于社区内部结构及其组织的重要信息。此外,掌握网络社区结构,可以提供网络未知区域的有用信息,帮助预防病毒或蠕虫扩散等潜在网络威胁。文献[2-3]对静态网络社区检测进行了研究。
然而,现实世界的社交网络并不总是静态的。实际上,大多数社交网络(如Facebook、Bebo和Twitter)处在发展变化中,随着用户数量的不断上升,网络规模和空间也在不断发展,因此,这些网络属于动态网络。动态网络是一种非常特殊的进化类型复杂网络,这种网络会随着时间的变化而不断变化。动态社交网络的拓扑结构变化太快且不可预测,大大增加了网络社区结构检测的难度和复杂性。
虽然网络更新后,可以运行现有的各种静态社区检测算法[2-4]来确定新的社区结构,但是仍然会存在一些无法回避的问题:(1)面对大型网络时,静态算法耗时太长;(2)局部最优陷阱;(3)网络发生局部微小变化时,算法响应几乎完全相同。完成这一艰巨任务的效果更佳、效率更高、耗时更少的方法就是根据先前网络结构对网络社区进行自适应更新,避免重新计算,本文的研究正是围绕这种自适应算法展开的,在保证社区检测准确性的前提下,满足社交网络用户的多样化需求。
2 相关工作
人们对静态网络的社区检测已经做了大量研究,并且针对这种网络提出了多种高效的检测算法。然而,对于动态网络社区结构检测方面的研究并不多。文献[4]提出一种新的基于k-派系渗透的动态网络社区检测算法。该算法可以检测重叠社区,但是耗时较长,对于大型网络更是如此。文献[5]提出一种基于网络拓扑矛盾和拓扑概率的检测算法,其中的拓扑概率是指一对节点参与某个社区的概率。该算法随着网络社区规模的增加,检测的效率和效果急速下降,不适用于大规模社交网络。文献[6]提出一种基于信息论交互信息和熵函数的无参数算法,用于图形进化时检测聚类。文献[7]提出一种分布式社区检测算法,该算法使用模性代替目标函数作为检测指标。文献[8]试图基于部分静态网络快照来跟踪社区随时间进化情况。然而文献[6-8]中的方法都无法避免重新计算的问题,
另外,文献[9]提出一种基于常量因子近似的动态社区检测算法。但是,该算法需要事先定义的惩罚成本,而动态网络往往无法知晓,因此该算法对现实世界的社交网络不具有可行性。文献[10]提出一种MANET网络社交感知路由策略,该策略基于模性的处理步骤MIEN可以快速更新网络结构。且MIEN可以生成/分解网络社区以适应网络变化,同时使用快速模性算法[11]以更新网络社区。然而,该算法由于复杂度较高,应用于大型动态网络时运行速度较慢。鉴于此,本文在已有工作的基础上,提出一种用于社区结构检测的自适应算法,并基于现实世界的动态社交网络和MANET社交感知路由验证其有效性。
3 问题建模
设 G=(V,E)为表示社交网络的无向未加权图,具有N个节点和M条链接。设 c={C1,C2,…,Ck}表示一组独立的网络社区,其中,Ci∈c是图G的一个社区。对各个顶点u,用 du,C(u),N C(u)分别表示该顶点的度、包含该顶点的社区及其相邻社区。此外,用分别表示总顶点集S内的链接数量、S的总顶点度,以及u至S间的链接数量。术语“社区”和“模块”、“节点”和“顶点”、“链接”和“边”可以互换使用。
定义1(动态社交网络)设 Gs=(Vs,Es)表示时间S时的网络快照,且网络快照与时间相关。用 ΔVs、 ΔEs分别表示时间S时将要引入(或去除)的节点集和链路集,Δ Gs=(Δ Vs,Δ Es)表示整个网络发生的变化。下一时刻的网络快照 Gs+1是当前网络快照和网络变化的结合:Gs+1=Gs∪ ΔGs。动态网络g是随着时间变化而不断进化的一组网络快照序列:g=(G0,G1,…,Gs)。
定义2(目标函数)为了对网络社区结构的品质进行定量描述,引用文献[12]提出的最被广泛接受的指标:模性ℑ,定义为。一般地,ℑ是社区所有链路比例减去图中相同数量的期望值,该图的节点具有相同的度数且链路随机分布。模性ℑ越高,网络社区结构越优。于是,本文的目标就是针对网络中的各个节点,确定一种社区分配使ℑ最大。与社区检测其他质量指标类似,指标ℑ在局部性、标度[3]和分辨率等方面存在一定缺陷。但是ℑ指标的鲁棒性和可用性与人们对各种真实世界网络的感知非常吻合,因此仍然得到广泛应用。
问题描述:设有动态社交网络 g=(G0,G1,…,Gs),G0是初始网络,G1,G2,…,Gs是基于 ΔG1,Δ G2,…,Δ Gs获得的网络快照。需要确定一种自适应算法,以根据先前网络快照高效检测任意时刻的网络社区结构,同时跟踪网络社区结构的进化情况。
4 改进的社区检测算法
在此首先讨论网络拓扑结构进化时发生的变化对社区结构的影响。假设 G=(V,E)是当前网络,c={C1,C2,…,Ck}是相应的社区结构。使用术语“区内链路”来表示2个端点均位于同一社区的链路,术语“区间链路”表示2个端点位于不同社区的链路。对G的各个社区C,将C与其他社区连接起来的链路数量,要远低于C内链路数量;也就是说,C内节点的连接程度要比外部节点密集。可以看出,向社区内增加区内链接,或者是去除图G的区间链接,均可以增加这些社区的强度,使图G的结构更加清晰。反过来,去除区内链接或者增加区间链接将会弱化图G的结构。然而,如果2个社区互相之间干扰较少,那么增加或者去除链接可以增加2个社区的吸引力,使得它们可以结合起来形成一个新的社区。于是,社区更新是一个非常复杂的过程,原因就是网络拓扑中的任何微小变化都可能让社区结构发生难以预料的变化。
为了反映社交网络发生的变化,通过插入或删除一个或一组节点、一条或一组链路,对图进行持续更新。实际上,加入或删除的节点(或链路)集合可以被分解成一组节点(或链路)的加入或删除,其中,每次只加入或删除一个节点(或链路)。这一结论可以把网络变化看成是简单事件的一个组合,其中的简单事件是指加入节点、去除节点、加入链接、去除链接4种事件中的一种。具体内容如下:(1)加入节点(V +u):新节点u及其相关链接加入。连同u加入的链接数量可以是0条,也可以是多条。(2)去除节点(V -u):节点u及其相关链接从网络中去除。(3)加入链接(E +e):连接现有2个节点的新链接e加入网络。(4)去除链接(E -e):网络现有链接e从网络中去除。
4.1 新节点的加入
首先考虑第一种情况,新节点u及其相关链接加入网络。注意,u可能没有相邻链接,也可能有多个链接连接了一或多个社区。如果u没有相邻链接,创建只包含u的一个新的社区,其余社区及总模性ℑ保持不变。当u有多个链接连接一个或多个当前社区时,情况就会变得有趣起来。此时需要确定,u应该加入哪个社区,使获得的模性最大。处理这一问题有多种局部算法[14]。本文算法受到文献[15]的物理算法启发,该算法中的每个节点受到2种力的影响:,使u保持在社区C内;社区C产生的使u属于C的力。定义如下:其中,doutS与dS的含义相反。
具体过程见算法1。

4.2 新的链接
假设有新的链接 e=(u,υ)加入网络,该链接连接了当前2个节点u,υ。将这种情况再细分为2个子情况:e是区内链接(完全位于社区C内);e是区间链接(连接 C(u),C(υ)2个社区)。根据引理1,如果e位于社区C内,则会增强C的内部结构。此外,根据引理2可知,添加e不应该导致当前社区C被分割成多个小社区。因此,在这种情况下,让当前网络结构保持不变。
引理1对任意C∈c,如果 dC≤ M-1,则在C内加入一条链接可以增加C的模性贡献度。
定理2如果C是图G当前快照下的一个社区,则向C中加入任意区内链接不会导致社区C被分割成多个小社区。
引理2如果新加入的链接(u,υ) 连接2个社区 C(u),C(υ),则如果(u或υ)欲更新其社区隶属,C(v()或 C(u))是其最佳社区选择。
当链接e连接了社区 C(u),C(υ)时可以发现,e的存在有可能让 u(或者υ)脱离当前社区而加入到新的社区。另外,如果 u(或者υ)决定改变其社区属性,它可以把新的社区信息发送给所有相邻节点,部分相邻节点可能会因此试图改变社区隶属。根据引理2,如果u(或者υ)欲改变其聚类分配,则 C(v()或 者C(u))是各自新的最佳社区归属。那么,当链接e加入时,应该如何迅速确定u(或者υ)是否应该改变其社区隶属以形成更优社区结构。为此,在定理3中提出一种节点u和υ隶属更改测试指标。此时,如果Δqu,C,D和Δqv,C,D均没有满足该指标,则可以维持当前网络社区结构,继续前进(推论)。否则,通过局部搜索和交换技术实现获得的模性最大化,进而让节点u,υ隶属新的社区,相邻节点确定欲加入的最优社区。
定理3假设新的链接(u,v)加入图G。设 C≡C(u)且D≡C(υ)。如果:
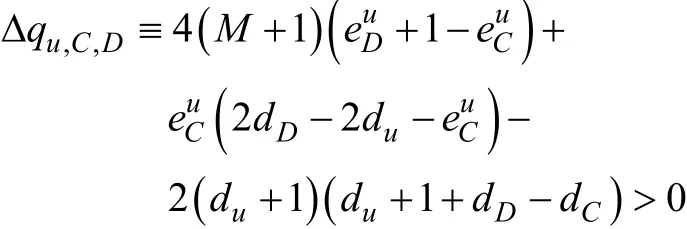
则把u加入D将会增加总模性。
推论 如果定理3中的条件没有满足,则不应该把u(或υ)及其相邻节点加入到社区D中。
图1描述了后一种情况的处理步骤。
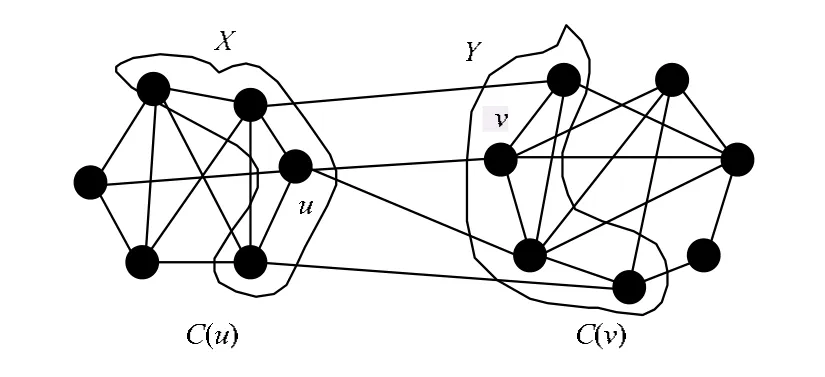
图1 网络拓扑进化对社区结构的影响
在图1中,连接 C(u)和C(υ)的链接(u,υ)加入网络。对集合X和Y进行社区隶属更改测试,具体过程见算法2。

4.3 节点的删除
当在时刻t把社区C的当前节点u删除时,该节点的所有相邻链接也同时删除。由于此时生成的社区非常复杂,因此这种情况处理起来难度很大:生成的社区可能没有变化,也有可能划分成多个子社区,或与其他社区结合。为了对此有进一步了解,考虑2个极端情况:删除的某个节点的度为1,删除的某个节点的度最大。如果度为1的节点被删除,则删除后的社区没有变化(引理3)。然而,当度数非常大的节点被删除时(如图2所示),当前社区可能会被拆分为多个小社区,进而与其他社区融合。因此,当C中某个节点被删除时,需要检测删除节点后C的结构。
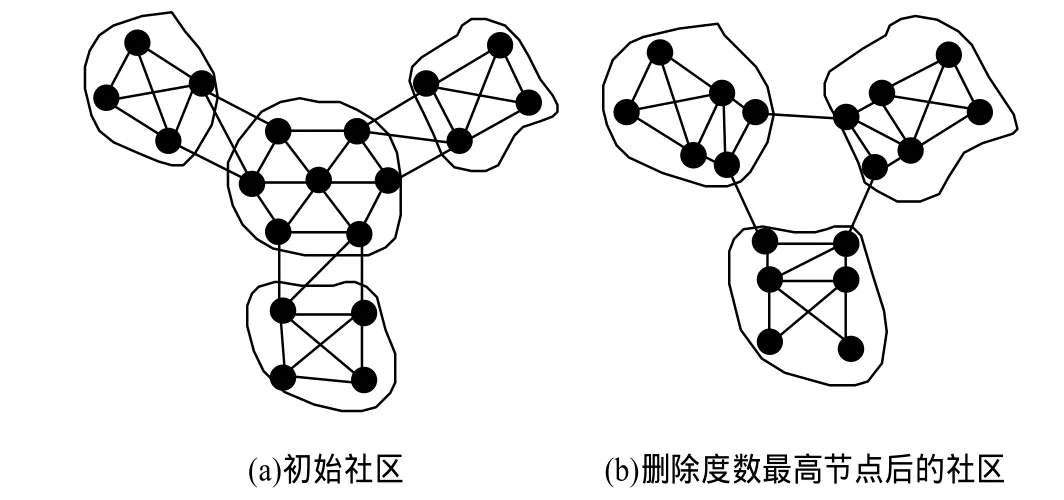
图2 新社区的形成
引理3如果C1和C2是G的2个社区,那么删除连接这2个社区的区间链接将会增加C1和C2的模性贡献值。
为了快速有效地处理这种情况,利用文献[2]中提出的派系过滤算法。尤其当节点u从C中删除时,对其个相邻节点设置3-派系,实施派系过滤,直到C中没有节点被发现(见图3,当中央节点g删除后,对a设置3-派系过滤,检测到b,c,d,e。随后 f落单)。然后,让C剩余社区选择各自最佳融合社区。具体算法见算法3。
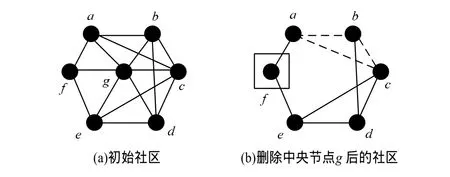
图3 社区融合

4.4 链接的删除
当欲删除链接 e=(u,υ)时,可以具体分为4种子情况:(1)e是个只连接u和υ的单边,其中,u和υ的度均为1;(2)u和υ中只有一个节点的度为1;(3)e是个连接 C(u)和C(υ)的区间链路;(4)e是个区内链接。如果e是个单边,很明显删除e后的社区结构不会改变,同时生成2个单独节点u和υ。同样的结论适用于第2种子情况;根据引理4,u和υ中只有一个节点的度为1,使原先网络结构附加上顶点u和υ。当节点e是区间链路时,删除e将会加强当前网络社区结构(引理3),不会对社区结构造成改变。
引理4将社区C内的(u,υ) 删除,且u或υ的度为1,则不会导致C被分割。
最后一种子情况是删除区内连接,最为复杂。如图4所示,如果社区本身链接很密,则删除这种类型的链接不会让社区产生变化;然而,如果社区内的部分结构内凝力有限,互相之间连接不够紧密,则该社区有可能会被分割。因此,检测删除之后剩余社区的结构,非常复杂。当区内链接从宿主社区C中删除时,引理4为检测社区进而将其一分为二提供了一个便捷工具。然而,它需要对C的所有子集加以详细考察,这一过程非常耗时。请注意,在删除(u,υ) 前,内含这一链接的社区C在其内部应该具有紧密的连接,因此删除(u,υ)应该会在C的内部生成“准派系”结构。于是,在当前社区内确定所有最大“准派系”,让这些“准派系”(及剩余的单个节点)确定加入哪些最优社区。具体过程见算法4。
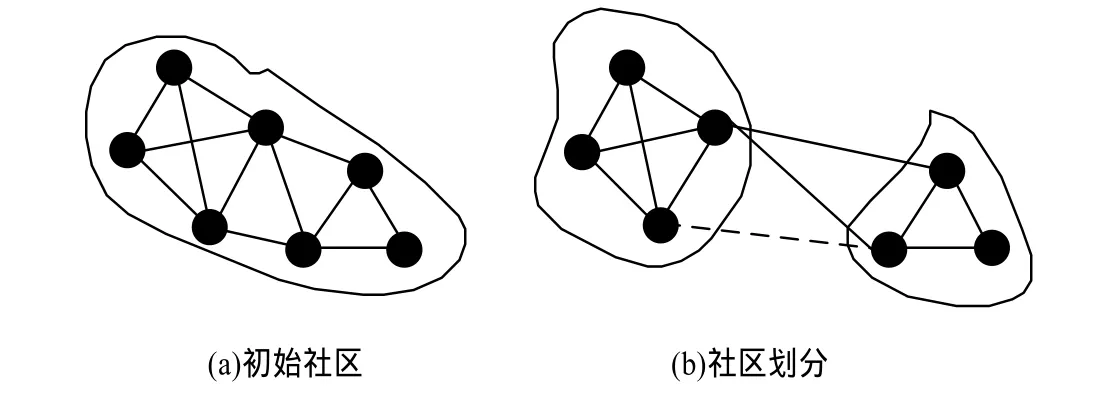
图4 链接的删除

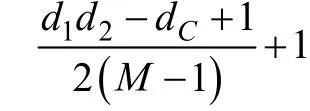
定理4(模性分割测试)对任意社区C,设α和β分别是C中度数最低的节点和度数第二高的节点。假设链接e从C中删除。如果没有子集C1⊆C和C2≡C C1满足以下条件:
(1)e越过C1和C2
则将C一分为二并不会使总体ℑ值上升。
4.5 本文算法
综上所述,本文提出的动态社交网络社区结构快速更新算法QCA的具体内容见算法5。


5 实验结果与分析
本节给出动态社交网络社区结构快速检测和更新算法QCA的实验结果。为了阐述本文算法的有效性,选用Facebook在线社交网络[16]进行了实验。比较对象是文献[13]中提出的静态检测算法(或称为Blondel算法)。除了静态算法外,还将QCA与文献[10]最近提出的动态自适应MIEN算法加以比较。MIEN算法将网络社区压缩或解压为节点,以适应网络变化,然后使用文献[14]中的快速社区检测算法对网络结构进行更新。且在实验中展现以下数值:(1)模性数值;(2)通过NMI分值衡量的网络社区质量;(3)本文QCA算法相对其他算法的处理时间。上述网络由于模性较高,因此包含的社区结构非常清晰,这也是本文选用上述网络的主要原因。
为了对发现社区结构的质量(即检测出来的社区与真实情况间的相似度)进行定量描述,采用信息理论领域常用的归一化交互信息(NMI)指标。NMI指标可靠性高,文献[2]将其应用于社区检测算法评估中。如果社区结构U和V完全分开时完全相同且均等于0,则 NMI(U,V)等于1。由于篇幅限制,可以阅读文献[3]获得NMI的完整表达式。
对各个网络,使用不同的方法提取时间信息,收集部分网络数据(往往是首个网络快照)以形成基本的网络社区结构。本文的QCA算法以此基本的社区结构为基础,只有网络发生变化时才会运行,此时必须在各时间点上针对整个网络快照运行静态算法。
Facebook网络数据集包含2009年9月-2012年1月期间新奥尔良Facebook局部网络的好友信息。为了收集信息,创建了几个Facebook账户,每个账户均加入局部网络,从单个用户开始缓慢发展,用广度优先搜索方式访问所有好友。数据集含有60k以上的节点(用户),150多万条好友链接,节点度数平均达到23.5。在本文实验中,2009年9月-2009年12月期间的节点和链接用于生成网络基本社区结构;在2010年1月-2012年1月期间,每月生成一次网络快照,共生成25个网络快照。实验结果如图5所示。
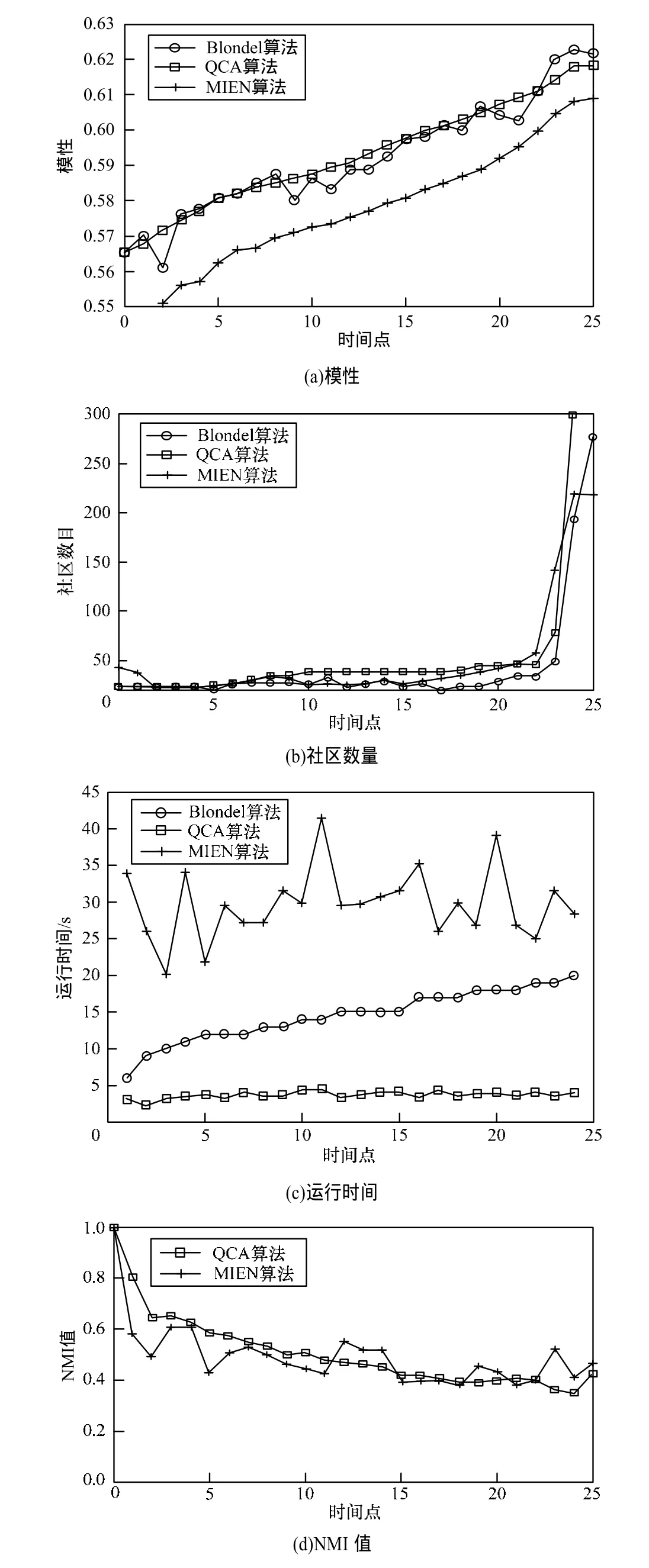
图5 Facebook社交网络仿真结果
图5(a)的评估结果表明,QCA算法的模性计算结果与静态算法相当,但是远高于MIEN算法。从总体趋势来说,QCA曲线与静态算法非常接近,且更加平稳。此外,实验结束时2种算法的最终模性结果基本相同,这意味着本文算法与针对整个网络的静态算法性能相当。
图5(c)描述了3种算法对Facebook数据集的运行时间。从图中可以看出,QCA成功计算和更新每个网络快照需要耗时至少3 s,最多4.5 s,而静态算法的耗时是QCA的3倍。MIEN算法面对Facebook大型网络时,耗时问题更加严重,所需时间是QCA算法的10倍以上。这一结果证明了本文算法应用于现实世界社交网络上的有效性;面对现实世界的社交网络,集中式算法往往无法在有限时间内有效检测出高质量社区结构。
6 应用示例
最近,部分研究人员指出,MANET具有社交网络特性,而具有社交感知功能的网络路由算法具有巨大潜力。这是因为人们倾向于在通信网络中形成多个群组或社区,各社区内个体互相之间的通信频率要高于与社区外个体的交流频率。网络社区结构检测对MANET移动自组网络的路由策略具有重要作用。对以下5种路由策略进行评估:(1)WAIT策略:源节点处于等待状态,不停发送或转发消息,直到遇到目的节点;(2)MCP策略:节点不停转发消息,直至达到跳跃最大值;(3)LABEL策略[17]:节点将消息发送或转发给目的社区的所有成员;(4)QCA策略:使用QCA算法作为动态社区检测技术的LABEL策略;(5)MIEN策略:对MANET网络使用社交感知路由策略[10]。
使用MIT媒体实验室提供的真实数据集[18]来测试本文算法。现实挖掘数据集包括MIT 100名学生在2011学年-2012学年的通信、附近、位置、活动信息。且该数据集还有相关学生350000 h(40年)期间的博客、附近蓝牙设备、手机信号塔编号、应用程序使用、手机状态(充电,空闲)信息。本文使用蓝牙信息生成底层MANET网络,对以上5种路由策略加以评估。
对各种路由策略,评估以下指标:(1)输送比:成功发送的消息与总消息之比;(2)平均输送时间:每条消息被发送的平均时间;(3)每条消息被发送时产生的消息副本平均数量。请注意,生成的1000条消息在实验期间内均匀分布,每条消息存在时间不得超过生存时间阈值。
实验结果如图6所示。图6(a)将输送比看成是生存时间的函数。如图所示,QCA的输送比远高于MIEN、LABEL和WAIT算法,这意味着QCA将消息从源节点成功发送至目的节点的数量高于其他算法。此外,当生存时间上升时,QCA算法的输送比趋近于输送比最高的MCP算法。如图6(c)所示,对输送时间比较后发现,QCA算法所需时间更少,消息成功传输速度高于LABEL算法。QCA算法的传输时间甚至要低于社交感知MIEN算法。具体原因如下:LABEL算法在实验期间最终改变其社区归属时,会将消息发往错误的社区。另外,OCA和MIEN算法在网络发生变化时可以迅速实现社区结构的检测和更新,因此性能更优。由于MIEN在网络进化时需要压缩/解压缩网络社区,因此可能忽略新生成的社区,导致需要额外时间转发消息。图6(b)显示的消息副本数量表明,QCA和MIEN在这方面性能最优。MCP算法的消息副本数量高于其他算法,此处没有绘出。实际上,QCA和MIEN算法结果相对接近;生存时间上升时,两者接近程度同步上升。总体来讲,QCA算法的输送比、输送时间和冗余度均优于其他算法,只在消息冗余度较低时劣于MCP算法,因此是5种路由策略中性能最优的社交感知路由策略。QCA算法的性能远高于基于静态社区检测的原始LABEL算法。以上结论证明本文自适应算法适用于MANET网络的路由策略。
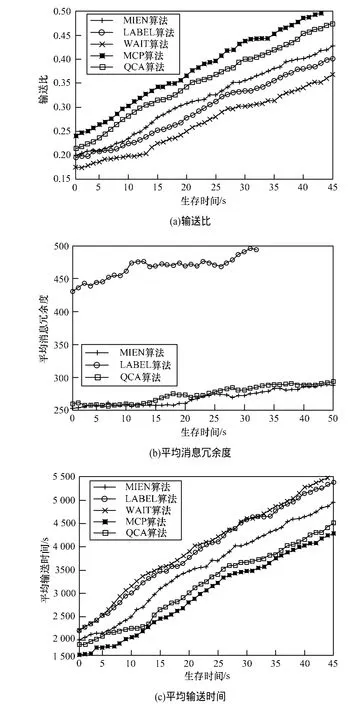
图6 不同算法在真实数据集下的实验结果
7 结束语
本文针对变化频率较高的动态社交网络,提出一种社区结构自适应检测算法QCA。该算法不仅可以有效更新检测高质量网络社区结构,而且运行时间较小,适宜变化频率很高的大型在线社交网络。将本文算法应用于MANET社交感知路由策略中,证明了QCA算法可以集成为社区检测内核,广泛应用于移动计算领域。下一步工作的重点是考虑社区内用户的共同兴趣度和社区间用户的兴趣相似度,研究基于兴趣感知的社区挖掘算法。
[1]乔秀全,杨 春,李晓峰,等.社交网络服务中一种基于用户上下文的信任度计算方法[J].计算机学报,2011,34(12):2403-2413.
[2]陈 琼,李辉辉,肖南峰.基于节点动态属性相似性的社会网络社区推荐算法[J].计算机应用,2010,30(5):1-5.
[3]Fortunato S.Community Detection in Graphs[J].Physics Reports,2010,486(3):75-174.
[4]Ahn Y Y,Bagrow J P,Lehmann S.Link Communities Reveal Multiscale Complexity in Networks[J]. Nature,2010,466(7307):761-764
[5]Zhang Yuzhou,Wang Jianyong,Wang Yi,et al.Parallel Community Detection on Large Networks with Propinquity Dynamics[C]//Proc.of the 15th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining.[S.l.]:ACM Press,2009:997-1006.
[6]Sun Jimeng,Faloutsos C,Papadimitriou S,et al.Graphscope:Parameter-free Mining of Large Time-evolving Graphs[C]//Proc.of the 13th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining.[S.l]:ACM Press,2007:687-696.
[7]Capocci A,Servedio V D P,Caldarelli G,et al.Detecting Communities in Large Networks[J].Physica A:Statistical Mechanics and Its Applications,2005,352(2):669-676.
[8]Hopcroft J,Khan O,Kulis B,et al.Tracking Evolving Communities in Large Linked Networks[J].Proceedings of the National Academy of Sciences of the United States of America,2012,101(S1):5249-5253.
[9]Tantipathananandh C,Berger-wolf T.Constant-factor Approximation Algorithms for Identifying Dynamic Communities[C]//Proc.of the 15th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining.[S.l.]:ACM Press,2009:827-836.
[10]Dinh T N,Xuan Ying,Thai M T.Towards Social-aware Routing in Dynamic Communication Networks[C]//Proc.of the 28th IEEE International on Performance Computing and Communications Conference.[S.l.]:IEEE Press,2009:161-168.
[11]Chen Duanbing,Fu Yan,Shang Mingsheng.A Fast and Efficient Heuristic Algorithm for Detecting Community Structures in Complex Networks[J].Physica A:Statistical Mechanics and Its Applications,2009,388(13):2741-2749.
[12]NewmanM E J,GirvanM.Finding and Evaluating Community Structure in Networks[J].Physical Review E,2004,69(2):261-269.
[13]Blondel V D,Guillaume J L,Lambiotte R,et al.Fast Unfolding of Communities in Large Networks[J].Journal of Statistical Mechanics:Theory and Experiment,2008,8(10):1742-1754.
[14]Newman M E J.Fast Algorithm for Detecting Community Structure in Networks[J].Physical Review E,2004,69(6):66-73.
[15]Ye Zhenqing,Hu Songnian,Yu Jun.Adaptive Clustering Algorithm for Community Detection in Complex Networks[J].Physical Review E,2008,78(4):461-468.
[16]马昱欣,徐佳逸,彭帝超,等.基于可视分析的多上下文移动社交网络社区发现[J].计算机科学与技术学报,2013,28(5):797-809.
[17]Pan Hui,Crowcroft J.How Small Labels Create Big Improvements[C]//Proc.of the 5th Annual IEEE International Conference on Pervasive Computing and Communications Workshops.[S.l.]:IEEE Press,2007:65-70.
[18]Eagle N,Pentland A.Reality Mining:Sensing Complex Social Systems[J].Personal and Ubiquitous Computing,2011,10(4):255-268.
