双心扰动量子粒子群优化算法研究

王安龙，何建华，陈 松，刘怀远

(西北工业大学电子信息学院，西安 710000)

1 概述

标准粒子群优化(Particle Swarm Optimization,PSO)算法无法以概率1收敛于全局最优解[1-2]，容易陷入局部最优。受微观世界概率随机性的启发，Sun J等人[3]于2004年在标准PSO的基础上，提出了量子粒子群优化算法(Quantum PSO,QPSO)。QPSO打破了标准PSO以轨道来描述粒子运动的模式，采用波函数来描述粒子的状态，增加了粒子在搜索空间内的概率随机性。随后，研究人员[4-9]对QPSO进行了改进，将遗传算法中的变异机制引入到QPSO中，实验证明，这是一种非常有效的方式。

针对QPSO的变异位置主要有：势能中心，重心和全局最好位置。粒子的势能中心能够吸引粒子在其邻域内探索新知识，对势能中心的变异能够产生新的个体结构[10-11]；粒子群重心代表了粒子群的主流思想[4]，对重心变异能够相对增加部分粒子的创造能力。为充分挖掘变异机制对算法的优化能力，本文提出了在2个位置协同变异的量子粒子群优化算法(BCD-QPSO)，进化前期以较小概率对势能中心和重心变异，发挥QPSO的全局搜索能力；进化后期以较大概率对势能中心和重心变异，保证粒子群的开拓能力。

2 标准QPSO算法

与标准PSO不同，在量子空间中，粒子的动量和位置不能同时具有确定的值，运动轨道不确定，在空间中的运动具有极大的随机性，这种随机性保证了QPSO的全局搜索能力。QPSO位置更新方程[4]为：

其中，xi(t)为第i个粒子的位置；Pi(t)和Pgb(t)为粒子i的历史最优位置和粒子群的全局最优位置；pi(t)和G(t)为粒子i的势能中心和粒子群的重心；β为收缩扩张系数。

3 双心扰动量子粒子群优化算法

3.1 变异算子

变异是粒子群多样性的产生机制，常用的变异方式有随机变异、高斯变异、柯西变异、混沌变异等[4]。高斯分布在变异点邻域产生小扰动的概率大而大扰动的概率小，而柯西分布正好相反，故选择柯西变异更能跳出局部最优。

柯西分布的密度函数为：

其中，α为尺度参数[10]，当α值较小时，概率曲线较凸，小尺度变异概率相对较大；当α值较大时，概率曲线较扁平，大尺度变异概率相对较大。本文采用文献[7]中的取值，即α=2.0。

3.2 变异概率自适应调整

到目前为止，在智能算法中采取的变异多数都是分阶段变异，迭代次数以离散序列增加决定了变异量自适应调整的非线性。设最大迭代次数为G，阶段数为S，则进化阶段可定义为G/S，特别地，当G=S时，分阶段变异退化为普通的自适应变异。

针对QPSO，有研究者[5-7]认为，前期较大的变异概率有利于产生新的个体结构，后期较小的变异概率有利于局部搜索。这种处理方式在一定程度上能提高算法的求解能力，但在进化后期对种群的引导力不足，使得粒子后期的创造能力有限。而本文采用的势能中心和重心协同变异，却能更保证进化后期粒子群的创造能力，对势能中心的变异，有利于提升单个粒子的创造力，而对重心的变异有利于提升整个粒子群的创造力。下面引入等差数列来描述变异概率逐步减小和变异概率逐步增大2种截然相反的变异策略。

变异概率约束条件：

其中，Pm(tk)表示第tk个进化阶段的变异概率。

等差数列法[12]：

3.3 BCD-QPSO步骤

BCD-QPSO步骤如下：

步骤1参数设置。设置最大迭代次数Gmax，搜索空间维数D，粒子群个体数目N。

步骤2种群初始化，利用一维Logistic混沌映射随机产生N个粒子。

步骤3计算每个粒子在解空间中适应度值，计算各个粒子自身最优适应度值pbest和粒子群的全局最优位置gbest。

步骤4进入主循环，确定进化阶段数，根据式(6)～式(9)计算自适应变异概率，并根据式(4)计算粒子群的重心，并对每个粒子按照式(3)构造一个势能中心。

步骤5根据自适应变异概率，对粒子群的重心和每个粒子的势能中心按照式(5)进行自适应柯西变异。

步骤6按照式(1)更新粒子群中每个粒子的位置。

步骤7更新每个粒子历史最优位置和粒子群的最优位置。

步骤8判断是否满足循环结束条件，如果不满足，则转到步骤4；如果满足循环结束条件，则输出最优解。

4 实验结果与分析

4.1 测试函数描述

本文采用的测试函数：Sphere，Rotated，Rastrigin，Griewank，下面对4个函数特点作简要阐述。

(1)Sphere函数

全局最优位置：f(x)=0,x(i)=0,1≤i≤ n ；函数曲面单峰、连续、对称。

(2)Rotated函数

全局最优位置：f(x)=0,x(i)=0,1≤i≤ n ；函数曲面单峰、连续、对称。

(3)Rastrigin函数

全局最优位置：f(x)=0,x(i)=0,1≤i≤ n ；函数曲面高度多峰、连续。

(4)Griewank函数

全局最优位置：f(x)=0,x(i)=0,1≤i≤ n ；函数曲面高度多峰、连续。

4.2 实验设计

本文以求4个函数的最小值为例，进行仿真实验，测试平台为Matlab R2011a，机器处理器为i3(2.13 GHz,3 MB L3 cache)，分别考虑6维和30维的情况，最大迭代次数设为1000，粒子数20，进化阶段为10，每种情况运行20次。实验中，分别测试了基于势能中心变异的量子粒子群优化算法(MPIL-QPSO)、基于重心变异的量子粒子群优化算法(MG-QPSO)、基于最优位置变异的量子粒子群优化算法(MGB-QPSO)和本文提出的双心扰动的量子粒子群优化算法(BCD-QPSO)。为更全面评价算法性能，采用2种截然相反的变异概率调整策略。策略1：取η=2.0，如图1细划线所示；策略2：取η=0.01，如图1粗划线所示。

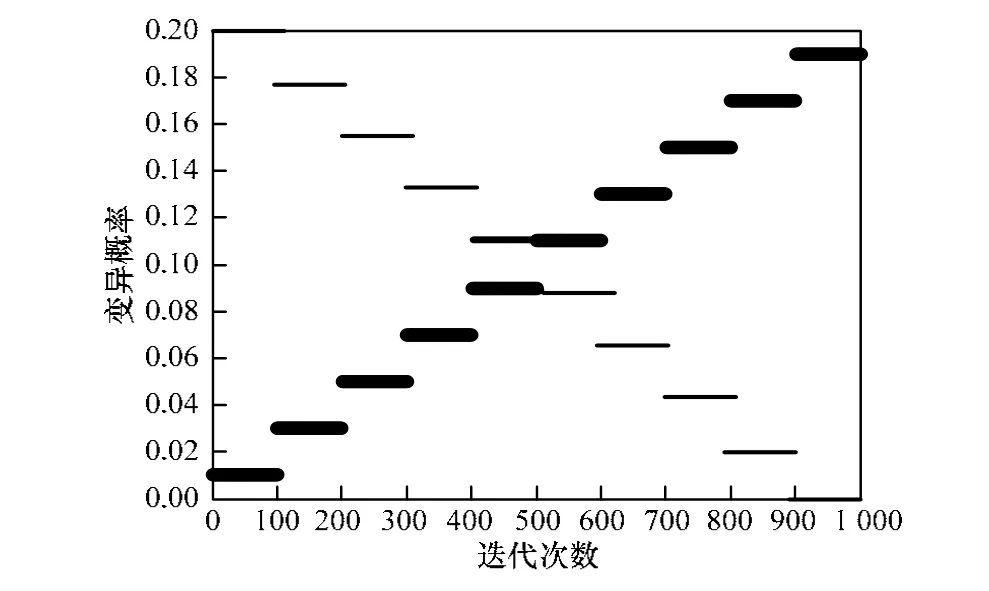
图1 变异概率调整

将数域(+∞,0]划分成n个子区间，对每个子区间按其相对重要性进行评分，并进行归一化处理，得到各子区间的区间权重w。本文设n=8，区间评分依次为1,2,3,4,5,6,7,8，归一化处理结果如表1所示。

下面定义一个新的测试指标：

定义 在N次独立重复实验中，落在第i个子区间的最优值数为ri，第i个子区间的区间权重为wi，则分布积分为：

分布积分越高，代表实验结果在高精度区间上的分布越多，算法性能越好，反之，算法性能越差。分布积分较好地反映了算法对目标函数的优化效果，区间划分越细，评价结果越全面。

表1 区间权重

4种函数测试结果如表2～表5所示，其中，粗体数字表示不同测试条件下目标函数的最优值。从表2、表3可以得出，在策略2下，针对单峰优化，3种单位置变异方式的最高分布积分为3.006,2.948,3.114,2.584，平均值为2.913；而BCD-QPSO的分布积分为4.216,4.020,4.049,3.612，平均值为：3.974，相对提高了36.42%。同理，从表4、表5可以得出，多峰优化时BCD-QPSO的优化效果比其他3种算法相对提高了32.84%。

表2 Sphere函数测试结果

表3 Rotated函数测试结果

表4 Rastrigin函数测试结果

表5 Griewank函数测试结果

图2和图3对比了不同策略下4种算法对不同测试函数的分布积分(量纲为1)，垂直柱状图中每组图形，从左到右依次表示MLIP-QPSO(字母A)、MG-QPSO(字母B)、MGB-QPSO(字母C)和BCD-QPSO(字母D)对相应测试函数优化结果的分布积分。

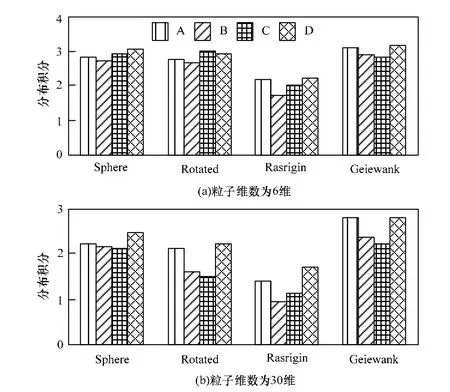
图2 策略1下的分布积分对比

图3 策略2下的分布积分对比

为了更加直观地反映BCD-QPSO的优化效率，本文绘出MLIP-QPSO、MG-QPSO和BCD-QPSO在求解Rastrigin函数时，前500代的算法收敛曲线(粒子维数30)。

从表2～表5可以得出：采取策略1时，MGB-QPSO优化效果不如其他3种算法；采取策略2时，算法后期震荡严重，局部搜索能力弱，优化效果不如标准QPSO。所以，图4和图5中没有绘出MGB-QPSO的收敛曲线。

图4 策略1各算法收敛曲线

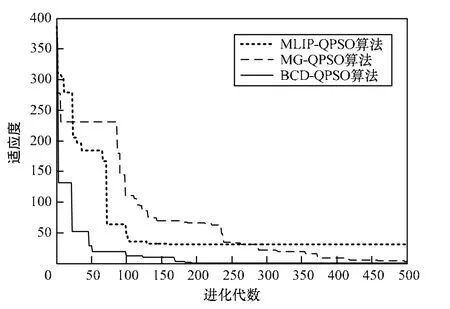
图5 策略2各算法收敛曲线

从以上4个函数的实验结果可以得出以下结论：

(1)不同的变异方式在不同的变异位置产生的效果不同。对全局最好位置和势能中心而言，采用变异概率自适应减小的变异策略，一定程度上抑制了早熟收敛，极大地提高了寻优能力，反之，则破坏了QPSO进化后期的局部搜索能力；对重心而言，采用变异概率自适应增大的变异策略，有利于进化后期粒子多样性的维护。

(2)采用双心扰动的变异方式产生蝴蝶效应，对单峰和多峰函数的优化能力都强于只采用单个位置变异的策略。

(3)无论是采取变异概率逐渐增大的变异概率调整策略，还是采取变异概率逐渐减小的变异概率调整策略，双心扰动变异产生的优化效果都好于单位置变异产生的优化效果，且适当的变异概率调整策略能大大提高算法的优化能力。

(4)BCD-QPSO的寻优能力和寻优效率不随变量维数的增加而明显减弱，在工程实践中有很好的应用前景。

5 结束语

本文提出了一种双心扰动量子粒子群优化算法(BCDQPSO)，通过与只采用单位置变异的量子粒子群优化算法仿真对比，证明了该算法具有收敛速度快、求解精度高的特点，同时适合于低维优化和高维优化，具有普适性。如何更好地挖掘组合变异机制的寻优潜力，进一步提高求解精度与效率，是今后的研究内容。

[1]van Den,Bergh F,Engelbrecht A P.A New Locally Convergent Particle Swarm Optimizer[C]//Proc. of IEEE Conference on Systems,Man and Cybernetics.[S.1.]:IEEE Press,2002:94-99.

[2]Clere M,Kennedy J.Particle Swarm Optimization Explosion,Stability,and Convergence in a Multidimensional Complex Space[J].IEEE Transactions on Evolutionary Computation,2002,6(1):58-73.

[3]Sun Jun,Feng Bin,Xu Wenbo.Particle Swarm Optimization with Particles Having Quantum Behavior[C]//Proc.of Conference on Evolutionary Computation.Piscataway,USA:[s.n.],2004:325-331.

[4]刘 静.粒子群优化算法研究及其在优化理论中的应用[D].无锡:江南大学,2007.

[5]向 毅,钟育彬.自适应阶段变异量子粒子群优化算法研究[J].计算机应用研究,2012,29(6):2035-2039.

[6]刘俊芳,高岳林.带自适应变异的量子粒子群优化算[J].计算机工程与应用,2011,47(3):41-43.

[7]李红婵,朱颢东.并行自适应量子粒子群优化算法[J].计算机工程,2011,37(5):221-223.

[8]钟文亮,王惠森,张 军,等.带启发性变异的粒子群优化算法[J].计算机工程与设计,2008,29(31):3402-3405.

[9]李 引,毛 力,须文波.量子粒子群优化改进的模糊C均值聚类算法[J].计算机工程与应用,2012,48(35):151-155.

[10]孙 俊.量子行为粒子群优化算法研究[D].无锡:江南大学,2009.

[11]施 展.多目标量子行为粒子群优化算法研究[D].南京:南京理工大学,2011.

[12]徐泽水.直觉模糊信息集成理论及应用[M].北京:科学出版社,2008:187-197.