时空神经网络及其在机场噪声预测中的应用
2014-09-29王尚北王建东陈海燕
王尚北,王建东,陈海燕
(南京航空航天大学计算机科学与技术学院,南京 210006)
1 概述
随着机场数量的增加和新型大型飞机的问世,机场噪声对周边环境的影响问题日益突出,越来越多因机场噪声引起的环境纠纷己成为航空业不可回避的棘手问题。因此,有效地预测机场噪声,是民航业可持续发展的重要课题。机场噪声监测系统在许多发达国家主要机场都已推广应用,北京首都国际机场、香港、台湾地区主要机场也已安装了类似系统。这些系统通过在机场周围设置的20个~40个固定监测点,24小时实时监测航空器噪声。在机场噪声监测系统中,不同监测点的噪声数据之间可能存在紧密的时空关联关系,充分利用监测点自身和近邻监测点的噪声数据以及它们之间的时空关联关系,从时空的角度研究机场噪声预测方法成为机场噪声预测的新方向。
现有的时空预测方法包括时空动力学方法[1]、状态空间和随机理论方法[2]、层次贝叶斯方法[3]和时空相关统计学方法[4]。其中,时空自相关移动平均模型[5](Space-time Autoregressive Moving Average,STARMA)充分考虑了时空自相关特征,更适用于时空数据建模。但是,STARMA模型在某些方面存在局限性,如STARMA模型在建模非平稳和非线性时空序列方面的理论和应用研究较少。人工智能等新的智能计算发展起来以后,人工神经网络等基于数据驱动的方法为时空序列建模提供了新的手段[6-7]。
本文在函数链接人工神经网络[8](Functional Link Arti-ficial Neural Network,FLANN)的基础上,结合线性脉冲响应滤波理论,提出一种新型时空神经网络。时空神经网络综合函数链接网络和线性脉冲响应滤波的优点,函数链接网络能够将输入空间映射到高维空间,实现输入空间的非线性模式到高维空间线性模式的转换,但函数链接网络只具有空间聚合能力,缺乏对时间延迟、积累效应的时间聚合能力。线性脉冲响应滤波原理恰恰弥补传统神经网络缺乏时间延迟、积累效应的时间聚合能力,因此,将线性脉冲响应滤波原理应用于函数链接网络,使其具有时、空二维聚合能力,并将其作为时空神经网络的函数扩展功能模块。现有研究从理论和经验证明时空数据序列可以分为线性部分和非线性部分,时空数据序列中的非线性部分可以由时空神经网络中函数扩展模块捕获,对于时空数据序列中的线性部分,时空神经网络引入线性脉冲响应滤波器,将其作为时空神经网络的线性脉冲延时模块,负责捕获时空数据序列中线性部分。
针对时空网络的学习算法,本文根据Levenberg Marquardt最优方法,设计时空神经网络的快速学习算法,以加快网络的收敛速度,提高网络的预测精度。最后针对机场噪声预测问题,给出一种基于时空神经网络的机场噪声预测方案。
2 函数链接人工神经网络
函数链接人工神经网络(FLANN[8])的结构如图1所示,网络输入为X=[x1,x2,…,xp]Τ,X为向量,网络输出为y。网络输入通过函数扩展被映射成高维(维数>p)空间的一组基φ1(x1),φ2(x1),…,φk(x1),…,φpk(xp)。

图1 函数链接人工神经网络模型
函数链接人工神经网络只有单层结构,相对于常规多层感知器神经网络,具有低计算复杂性和快速收敛特性。从图1中也可以看出,函数链接网络只具有空间聚合能力,缺乏对时间延迟、积累效应的时间聚合能力,这也是传统神经网络具有的共同特点。
3 时空神经网络
自从人类仿照生物神经元的信息处理机制,抽象出第一个人工神经元数学模型以来,经过人类的不断努力神经网络的研究取得丰硕成果,其应用领域也渗透到各个学科。但现有的人工神经网络模型大多处于PDP理论框架下,即每次网络的输入只是瞬时值或瞬时向量。现代的神经生理学实验和生物学研究表明,神经网络的输出不仅与输入信号的空间聚合和激励阈值有关,同时也依赖于输入过程中的时间累积效应。传统神经网络模拟了生物神经元的空间加权聚合,但缺乏对时间延迟和累积效应的描述。因此,本文在FLANN的基础上,结合线性脉冲响应滤波理论,提出一种新型时空神经网络,使其既对空间多输入的聚合,又有对时间积累效应的聚合,具有时空二维信息处理的能力。
3.1 线性脉冲响应滤波
为克服处于PDP理论框架下的神经网络缺乏对时间的延迟和积累效应的不足,本文引入线性脉冲响应滤波来实现神经网络对时间的延迟和积累效应。
线性脉冲响应滤波原理见图2,其通过延迟算子 Z-1实现了时间延迟,线性脉冲响应滤波的输出为:y(t)=,该输出实现了时间积累效应。

图2 线性脉冲响应滤波原理
3.2 时空神经网络结构
时空神经网络的结构如图3所示。其中,x1(t),x2(t),…,xp(t)为p个离散的网络输入值序列;Z-1为时间延迟算子,xi(t - 1)=Z-1xi(t)。

图3 时空神经网络
时空神经网络本质上是利用线性脉冲响应滤波原理而具有时、空二维聚合能力的函数链接网络,通过延时算子 Z-1引入输入值序列的历史数据 xi(t - 1),xi(t - 2),…,xi(t -N1),然后将历史数据连同输入值 xi(t)扩展为一系列线性独立的函数(三角函数、切比雪夫多项式、拉格朗日多项式等),这些函数可以看做扩展后高维空间的一组基。函数扩展功能模块将网络输入空间映射到一个高维空间,实现输入空间的非线性模式到高维空间线性模式的转换,然后使用高维空间上的一组基的线性组合拟合经过转换的时空序列非线性模式。
本文选用三角函数作为扩展函数,网络的输入向量X(t)=[x1(t),x2(t),…,xp(t)]T,通过函数扩展功能模块,输入向量可以表示为:

时空神经网络的下半部分为线性脉冲延时模块,线性脉冲延时模块针对每个输入 xi(t)构造一个线性脉冲响应滤波器,因此,可将线性脉冲延时模块认为是一个时空线性脉冲响应滤波器。网络输入向量 X(t)=[x1(t),x2(t),…,xp(t) ]T经过线性脉冲延时模块的作用可以表示为:
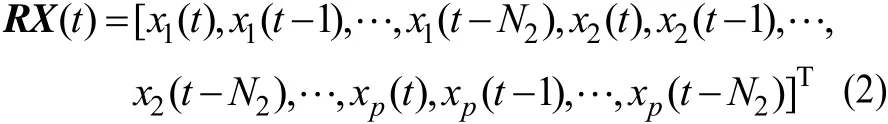
时空神经网络函数扩展功能模块的输出为:

时空神经网络线性脉冲延时模块的输出为:

S(·)为非线性传递函数,本文选取为tanh(x),则:

时空神经网络的输出为:

其中,λ为组合系数。现有文献证明了时空数据序列可分为线性部分和非线性部分,由图3可见,时空神经网络由函数扩展功能模块和线性脉冲延时模块组成。函数扩展功能模块通过将网络输入空间映射到一个高维空间捕获输入时空数据序列的非线性模式,线性脉冲延时模块则负责输入时空数据序列线性模式的拟合。之后通过组合系数λ将两部分有效整合。当λ取1时,时空神经网络仅有函数扩展功能模块;当λ取0时,时空神经网络仅有线性脉冲延时模块。当λ取0~1之间的值时,时空神经网络既包含函数扩展功能模块,又包含线性脉冲延时模块,并将2个模块捕获的非线性和线性模式有效整合,获得更好的预测效果。
3.3 时空神经网络快速学习算法
定义网络的误差为:
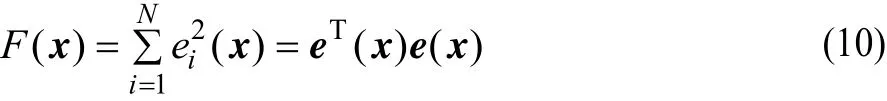
其中,N为样本数目;x=[w11,…,w1M,…,wpM,w1(M+1),…,为时空神经网络的参数向量;e(x)为第i个i样本的误差;为误差向量。
根据Levenberg-Marquardt最优方法得时空神经网络参数更新规则:

其中,J(xk)为雅可比矩阵。时空神经网络快速学习算法的关键是构造雅可比矩阵。误差向量和参数向量分别如式(12)和式(13)所示,则时空神经网络的雅可比矩阵可表示如式(14)所示。

对于函数扩展功能模块中的wab,雅可比矩阵中的元素:

对于线性脉冲延时模块中的wab,雅可比矩阵中的元素:

对于函数扩展功能模块和线性脉冲延时模块的组合系数λ,雅可比矩阵中的元素:
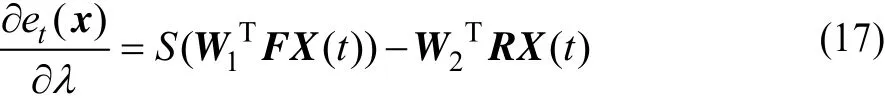
通过式(14)~式(17)可以求出时空神经网络的雅可比矩阵,然后通过式(11)不断更新时空神经网络的权值直到网络误差达到预先设定标准。
4 基于时空神经网络的机场噪声预测方案
基于时空神经网络的机场噪声预测方案如图4所示。

图4 基于时空网络的机场噪声预测方案
(1)噪声监测系统:通过机场周围设置的若干个固定监测点,24小时实时监测飞机噪声,为机场实施噪声预测提供较为可靠的原始噪声数据。图5为某机场噪声监测系统中监测点的分布。
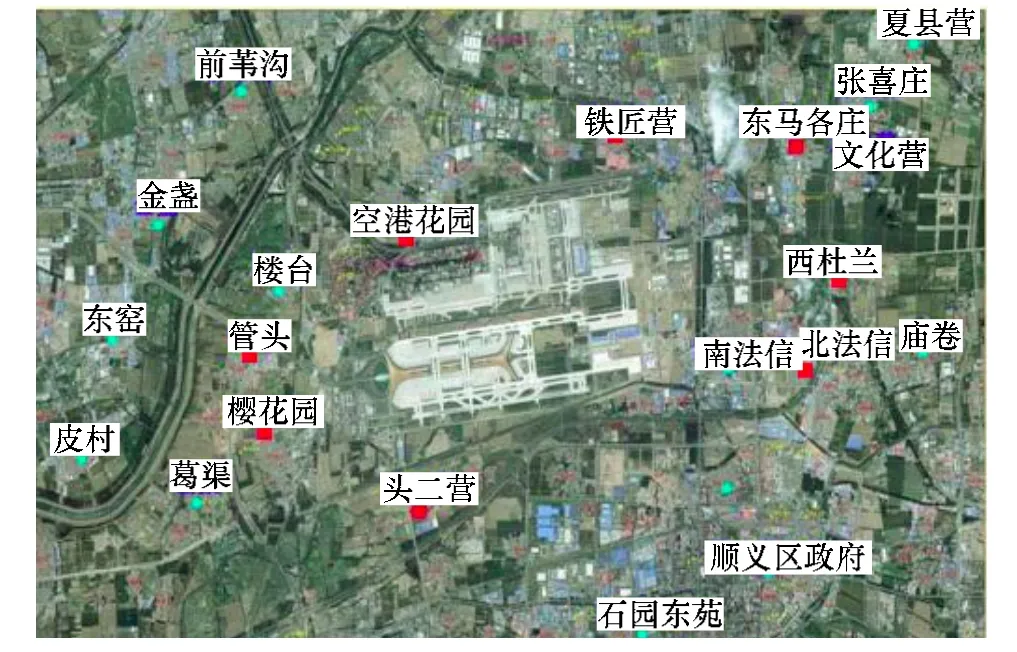
图5 某国际机场监测点分布
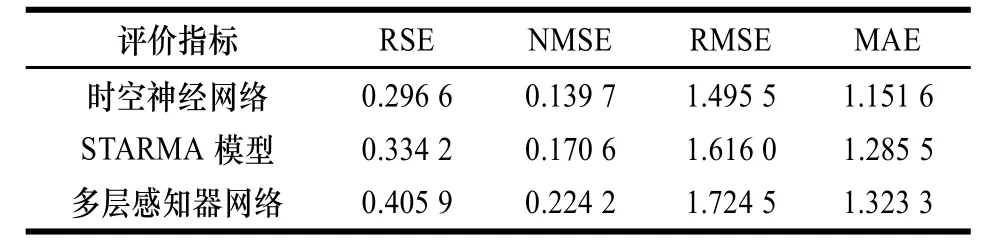
(2)相关性分析:由图5可见,有些噪声监测点间的距离很远,噪声序列之间近似于相互独立不存在空间关联关系。相关性分析利用文献[9]中的空间邻接K-means聚类算法选择具有空间关联关系的噪声监测点集合,集合中监测点个数为p(p (3)数据预处理:将相关性分析选择出的p个监测点的噪声序列进行归一化处理,假定Maxi为监测点i的噪声序列最大值;Mini为监测点i的噪声序列最小值;Zij为监测点i的噪声序列中第 j个元素值,数据预处理过程如下: 利用本文提出的时空神经网络进行机场噪声预测之前,需要确定时空神经网络的参数——时间延迟参数和函数扩展参数。 (4)时间延迟参数:线性脉冲响应滤波中时间延时算子的个数,对应于时空神经网络(图3)中时间延迟算子的个数,即式(1)和式(2)中N1和N2的大小,一般 N1=N2。文中采用GP算法[10]求时空网络p个噪声输入值序列的关联维数,时间延迟参数取p个关系维数中的最大值(向上取整)。 (5)函数扩展参数:函数扩展模块将 xi(t)扩展为多少个sin(πxi(t)),cos(πxi(t)),sin(2πxi(t)),cos(2πxi(t)),…,sin(kπxi(t)),cos(kπxi(t))函数,即式(1)中的k。 以某机场为例,机场布置了21个固定监测点,实时监测机场周围敏感点的噪声。历史数据表明,在21个监测点中有7个监测点数据常常缺失,因此,在机场噪声时空预测方案中,选择了其余14个监测点,分布如图5所示。实验的数据集为该机场2010年8月5日﹣2010年8月14日的8:00−18:00的噪声实测数据。为了平滑突发情况对监测点噪声数据的影响,将监测点时间间隔5 min的噪声数据取平均,每个监测点一天记录120条噪声数据,这样每个监测点提供1200条噪声实测数据。前960条噪声数据作为训练集,后240条噪声数据作为测试集。实验选取监测点5(西杜兰)为目标监测点,通过相关性分析选取与目标监测点具有较强相关性的监测点集合,即监测点3(东马各庄村)、监测点6(北法信)、监测点11(文化营)、监测点14(南法信)和监测点17(庙卷),然后进行数据预处理。 时空神经网络有6个噪声输入序列,网络中的函数扩展参数为2,时间延迟参数为3,学习算法采用文中的时空神经网络快速学习算法。采用相对平方误差(RSE)、正态均方误差(NMSE)、均方根误差(RMSE)和平均绝对误差(MAE)作为指标。实验首先检验时空神经网络通过组合系数λ将函数扩展功能模块和线性脉冲延时模块整合起来是否能够提高预测精度。为此,在机场噪声数据集上对比本文的时空神经网络(网络1)、只含函数扩展功能模块的时空神经网络(网络2)和只含线性脉冲延时模块的时空神经网络(网络3)的预测误差。3种时空神经网络的预测误差比较如表1所示。 表1 3种时空神经网络预测误差 实验结果表明,时空神经网络通过组合系数λ将函数扩展功能模块和线性脉冲延时模块整合能够提高预测精度。同时,也间接地表明机场噪声时空数据序列包含时空线性模式和时空非线性模式。 为进一步评估时空神经网络的性能,实验采用时空序列预测模型STARMA和时间序列预测模型多层感知器神经网络作为对比模型。实验中STARMA模型的形式为: 其中,空间权矩阵W0为单位矩阵,空间权矩阵W1为: STARMA模型的参数估计采用文献[11]提出的遗传算法。多层感知器神经网络模型为3层3-5-1网络结构,输入层有3个输入,分别为目标监测点5(西杜兰)的噪声序列值x5(t-1),x5(t-2),x5(t-3),隐藏层有5个神经元,输出层为目标监测点5的噪声序列值x5(t)。时空神经网络的预测结果如图6所示,STARMA模型预测结果如图7所示,STARMA模型参数为: 多层感知器神经网络预测结果见图8。 图6 时空神经网络预测结果 图7 STARMA模型预测结果 图8 多层感知器网络预测结果 利用上述指标评价3种预测模型的预测精度,结果见表2。可见,时空神经网络的预测精度高于STARMA模型和多层感知器网络。时空神经网络由函数扩展功能模块和线性延时脉冲模块组成,函数扩展功能模块负责捕获时空非线性模式,线性脉冲延时模块负责拟合时空线性模式。而STARMA模型由于模型条件约束,只能拟合时空序列中线性模式,比较表2中STARMA模型和表1中线性脉冲延时模块可发现两者相差不大。表1中结果间接表明机场噪声时空数据序列包含时空线性模式和时空非线性模式,因此,时空神经网络预测精度高于STARMA模型。同时,时空神经网络和STARMA模型的精度也高于多层感知器网络。 表2 3种模型的预测误差 实验中的噪声监测点通过相关性分析得到,这些监测点彼此之间存在显著的关联关系,时空神经网络和STARMA模型不仅利用目标监测点的历史信息,而且充分挖掘噪声监测点间的关联关系并将其应用到目标监测点的噪声预测中,因此,时空神经网络和STARMA模型的预测精度高于多层感知器神经网络。 针对时空序列预测问题,本文结合函数链接人工神经网络和线性脉冲响应滤波原理,提出了一种新型的时空神经网络,该时空神经网络能够同时拟合时空序列中的时空线性模式和时空非线性模式。机场噪声的仿真实验结果表明,时空神经网络的精度明显高于STARMA时空序列预测模型和多层感知器网络时间序列预测模型。时空神经网络不仅适合于机场噪声预测应用,同样也可以推广到其他时空序列预测领域。 [1]Viglione A,Chirico G B,Komma J,et al.Quantifying Spacetime Dynamics of Flood Event Types[J].Journal of Hydrology,2010,394(1):213-229. [2]Mhanna M,Bauwens W.A Stochastic Space-time Model for the Generation of Daily Rainfall in the Gaza Strip[J].International Journal of Climatology,2012,32(7):1098-1112. [3]Lee S D,Kim D K.Bayesian Inferences and Forecasting in Spatial Time Series Models[C]//Proc.of ICMLA’10.[S.l.]:IEEE Press,2010:767-770. [4]Pfeifer P E,Deutrch S J.A Three-stage Iterative Procedure for Space-time Modeling Phillip[J].Technometrics,1980,22(1):35-47. [5]韩卫国,王劲峰,高一鸽,等.区域交通流的时空预测与分析[J].公路交通科学,2007,24(6):92-96. [6]梅志雄.应用 DRNN和 ARIMA组合模型的时空集成预测方法[J].小型微型计算机系统,2010,31(4):657-661. [7]常 刚,张 毅,姚丹亚.基于时空依赖性的区域路网短时交通流预测模型[J].清华大学学报:自然科学版,2013,53(2):215-221. [8]Zhao Haiquan,Zhang Jiashu.Adaptively Combined FIR and Functional Link Artificial Neural Network Equalizer for Nonlinear Communication Channel[J].IEEE Transactions on Neural Networks,2009,20(4):665-674. [9]王海起,王劲峰.一种基于空间邻接关系K-means聚类算法改进[J].计算机工程,2006,32(21):50-51. [10]Grassberger P,Procaccia I.Measuring the Strangeness of Strange Attractors[J].Physica D:Nonlinear Phenomena,1983,9(1):189-208. [11]Halim S,Bisono I N,Sunyoto D,et al.Parameter Estimation of Space-time Model Using Genetic Algorithm[C]//Proc.of IEEM’09.[S.l.]:IEEE Press,2009:1371-1375.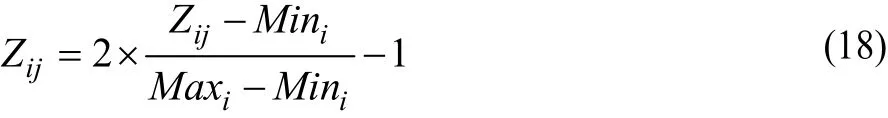
5 实验及结果分析



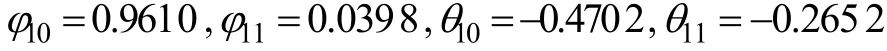



6 结束语
