基于贝叶斯网络的运动想象脑电信号分析

刘 斌，罗 聪，魏梦然，何良华

(同济大学计算机科学与技术系，上海 201804)

1 概述

自1929年德国精神病学专家Hans Berger发现并记录人的脑电信号以来，国内外的专家学者对脑电信号进行了大量的研究，取得了显著的效果。近年来随着科学技术的发展，尤其是随着脑机接口(Brain Computer Interface,BCI)技术的出现，使得对运动想象脑电信号的研究成为一个新的研究热点。

针对脑电信号的处理分析尤其是对运动想象脑电信号的处理分析，众多学者提出了很多判别计算方法，主要有基于不同脑电波段进行分析[1]、基于自回归模型算法[2]、基于小波变换[3]、线性判别方法[4]、神经网络等[5]。上述研究将运动想象的脑电分析问题看成是模式分类，对不同运动想象模式提取特征，如频率和回归系数等，然后构建判别分析模型进行判别分析。在一定的条件下这些方法取得了很好的结果，不足之处在于很少考虑到脑电信号的特点，即时间空间分布特征显著，因此，本文提出了基于贝叶斯网络的判别分析思想，通过图模型的空间逻辑结构模拟导联的空间位置，各节点的分布建模模拟导联的时间特征。

贝叶斯网络是一种表示变量间概率分布的图形模型，它充分综合了先验知识以及数据分布特征，并以图论方法准确地描述出变量之间的因果关系[6-7]。目前贝叶斯网络在脑电方面的应用主要是做特征提取，文献[8]利用贝叶斯网络方法分析处理不同情感下的脑电数据来进行情感识别，文献[9-10]则用贝叶斯网络进行汽车驾驶员的疲劳状态的识别。

在已往研究中针对的贝叶斯网络算法中，其变量主要是针对离散变量，而在实际应用中，对如脑电信号这种连续变量也往往是采用连续数据离散化的方法进行贝叶斯网络结构学习。离散过程中会丢失很多数据包含的信息，甚至可能出现假依赖的现象[11]。除了离散化之外，对于连续变量，还有一种方法是基于条件独立性测试，文献[12]将信息论与统计测试结合起来，通过计算互信息来确定节点之间的条件独立性，从而构造多连接有向图模型。虽然这种方法在一定程度上能够反映连续变量之间的相互关系，但是文献[13]已经指出，这种算法的缺点在于，在有限的样本空间内，高阶的条件独立性检验的结果极有可能是不可靠的。

本文针对左右运动想象的连续脑电信号，提出一种基于高斯分布的贝叶斯网络结构运动想象脑电信号分类方法，主要有以下创新：(1)分别构建左右运动想象的贝叶斯网络，再通过网络结构的差异性来进行相关统计分析；(2)在结构学习搜索过程中添加根据脑电导联物理位置关系约束；(3)在评分过程中采用高斯分布来描述每个导联的脑电数据，进而获得连续变量的相关参数和概率密度函数。

2 基于贝叶斯网络的运动想象脑电信号分类

2.1 贝叶斯网络结构学习

贝叶斯网络是一个有向无圈图，由网络结构和条件概率分布组成[14]。设节点代表各个导联，节点间的边代表导联之间的相互关系。本文的贝叶斯网络结构学习步骤如下：

(1)根据Fisher判别准则确定任意两节点是否独立，从而得到每个节点的父子节点集Π1；考虑到越相近的导联获取脑电信号所包含的神经活动越相近，本文再根据导联的物理位置分布选取出每个导联的四邻域导联作为其父子节点集Π2，于是取 Π=Π1∩Π2作为最终的父子节点集。

(2)对样本集进行结构学习。对每个节点进行高斯分布建模，在此基础上采用经典的贝叶斯信息准则(Bayesian Information Criterion,BIC)[15]对整个贝叶斯网络进行评分。

2.2 基于高斯分布的评分方法

对于连续脑电信号的概率密度函数，本文通过高斯分布来表示，下面介绍具体的算法推导及过程。

现已知某导联Xi及其连续父节点Y，则其条件概率密度可表示为：

其中，Bi是权值矩阵；μi表示均值；∑i表示协方差矩阵。

若存在m个独立同分布样本集D，则上式的最大似然估计可表示为：

将式(1)带入式(2)，则式(2)可转变为以下形式：

通过上式进行最大似然估计即可得到相应的均值、协方差和权值，结果分别为：

其中，E[XY′]表示子节点X的样本与父节点Y样本的转置的条件二阶矩，其余表达式类似。

BIC评分是一种常用的评分方法，计算公式如下：

其中，LL表示极大似然估计的对数；d表示参数的个数；n表示变量的个数。

对于连续变量，通过计算变量概率密度或者条件概率密度的极大似然估计来进行评分，如式(6)所示：

其中，Θ表示连续分布的相关参数；m表示样本个数。

给定样本数据即可通过上式分别计算出均值、协方差和权值，再代入式(1)即可得到概率密度函数，继而得到整个网络的得分情况，该评分方法的流程如图1所示。

图1 基于单高斯分布的评分流程

2.3 本文方法流程

本文提出的基于贝叶斯网络的运动想象脑电信号分析方法流程如图2所示。

图2 基于贝叶斯网络的运动想象脑电信号分析流程

3 运动想象实验

3.1 实验数据来源

本文实验数据来源分为2组：第1组来源于Graz大学的国际BCI竞赛数据(BCI IIIa)，该数据集中包含3个被试验对象(下文中简称被试)，每个被试进行4种运动想象，本文分别取每个被试的30个左、右手运动想象数据来进行分析。另外，为了验证本文方法的通用性，本文按照第3届国际BCI竞赛实验设计运动想象实验，并采集测试数据，这同时也是本文的第2组数据。实验数据采用64导的G.tech脑电放大器采集获得，采样频率为250 Hz。被试对象为5名在校学生，男性，健康状况良好，年龄在23岁～27岁之间。实验过程中被试头戴脑电帽，放松地坐在椅子上，按照电脑屏幕上随机提示想象左手或右手运动。单次运动想象时间持续7 s，其中，前2 s被试处于安静状态，2 s时计算机发出提示音并在屏幕中央显示“+”，3 s时计算机屏幕上出现向左或者向右的箭头，被试开始进行运动想象，该过程一直持续到第7 s。每个被试分别进行30个左、右手运动想象。

3.2 数据预处理

对2组数据随机取其中20个作为训练样本，剩余10个作为测试样本。综合贝叶斯网络构建的复杂度及前人的研究成果，本文选取11导(FC3,FC4,C5,C3,C1,CZ,C2,C4,C6,CP3,CP4)数据进行分析。在分析之前，本文对实验数据进行了预处理。预处理主要是进行去除眼电和进行滤波工作。眼电的去除借助Neuroscan软件完成。对于滤波工作，本文分析的频带为8 Hz～30 Hz，正好是α波和β波的频带[16]。因此，本文设计椭圆滤波器，其通带频段为8 Hz～30 Hz。

3.3 实验结果与分析

3.3.1 BCI IIIa实验结果

在分析过程中，BCI IIIa数据集中的3组(k3b、k6b、l1b)被试的每种类型的运动想象样本可以得到一个相应的贝叶斯网络，将每种类型的20个贝叶斯网络的共同边属性进行统计，得出可用于区分的边和方向。

实验结果如图3所示(本文取被试k3b的统计图进行说明)，图中横坐标对应导联的编号，纵坐标表示20个训练样本中以某导联为父节点的相应边出现的次数。图3(a)表示左运动想象贝叶斯网络相加统计结果；图3(b)表示右运动想象贝叶斯网络相加统计图；图3(c)则表示两者相减之后的结果。

在所有3个被试的2类运动想象中，左右运动想象的贝叶斯网络差值都有显著性差异边存在，但不相同。例如，对被试k3b，显著性差异的边为导联1到导联4所构成的边。表1展示的是3个被试显著性差异的边及差异程度，括号内的数字表示差异程度(即对应边显著性差异的运动想象样本个数)，其中，正数表示左右显著性差异程度，负号则表示右左显著性差异程度。在判别分析过程中，根据网络中这些显著性差异边就能就能识别运动想象的类型。

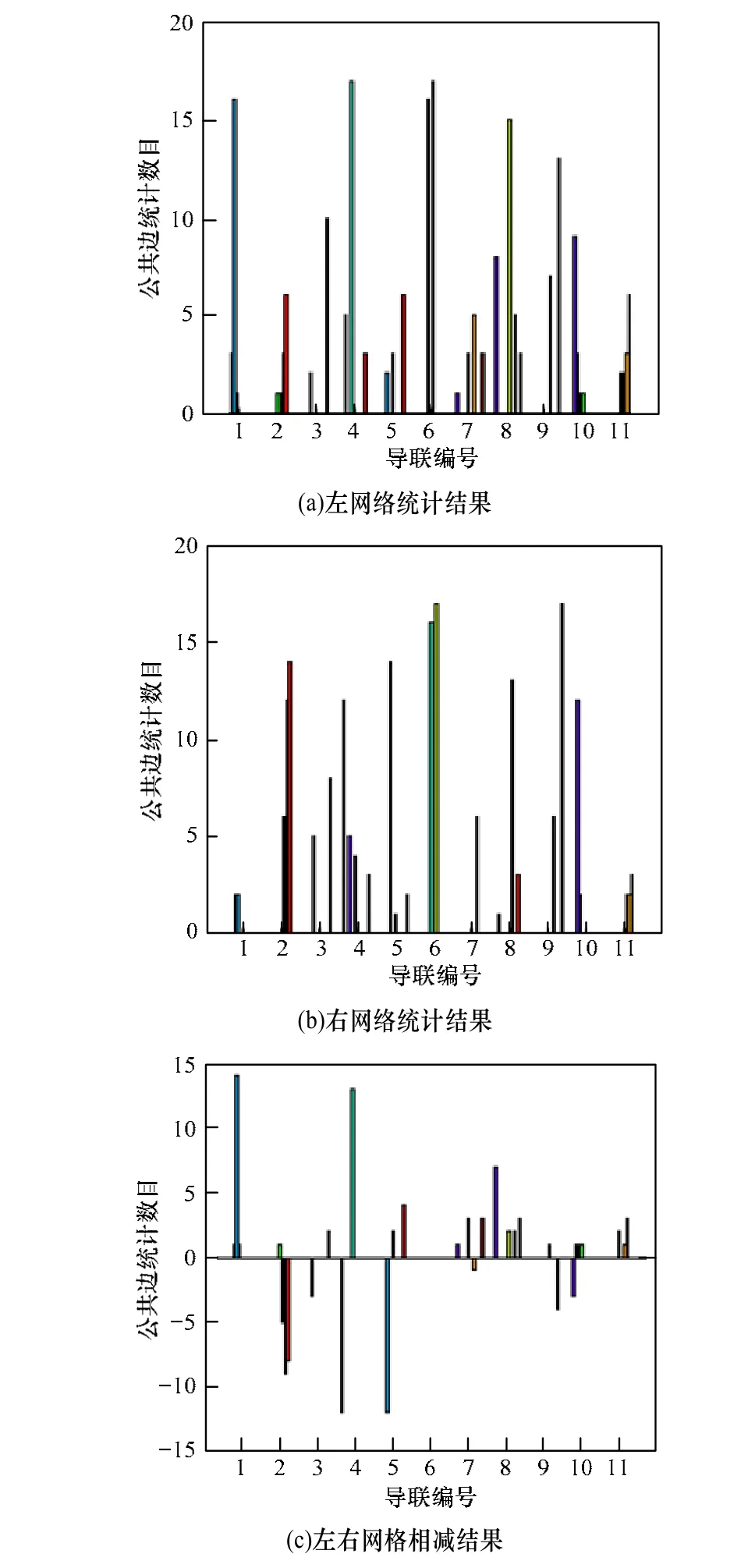
图3 k3b左右统计结果

表1 BCI IIIa贝叶斯网络公共边统计结果

对于上述3个标准数据集，为了体现出本文方法的有效性，采用文献[17]的实验结果作为对比，同时采用文献[18]的PCA+fisherscore方法进行判别分析，3种方法的识别率如表2所示。可以看出，本文方法的平均识别率为76.67%，而文献[18]的PCA+Fisherscore方法识别效果较差，平均识别率仅为45.55%；文献[17]提出的基于时频域分析的运动想象脑电信号分类方法是近来取得较好识别效果的一种方法之一，虽然对特定的数据集可能存在较好的效果，但该方法的平均识别率为76.47%，依然略差于本文方法的平均识别率。

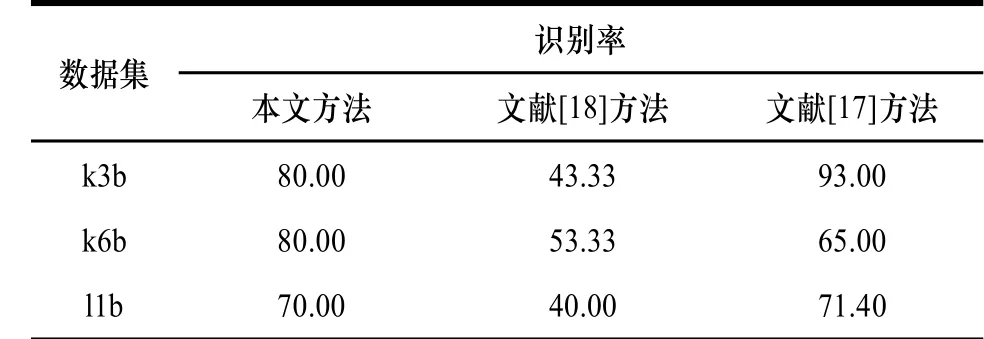
表2 BCI IIIa数据左右运动想象识别率 %

3.3.2 自测数据实验结果

对本文所用的5个被试实验数据，同样按照上组实验方法进行统计，得到如图4所示的统计结果。

图4 被试1的左右统计结果

表3展示了测试组所有5个被试显著性差异的边及相应的差异程度。

表3 贝叶斯网络公共边统计结果

为直观地显示出网络结构的差异，图5给出了被试实验数据1的左、右运动想象贝叶斯网络图及最大差异边的示意图。其中，圆圈表示左右显著性差异最大的边，即用来进行左右判别的边。

图5 被试实验数据1左右运动想象贝叶斯网络

针对测试组5个被试，同样采用PCA+fisherscore方法进行判别分析。2种方法的得到的识别率如表4所示。

表4 5组左右运动想象识别率 %

由表4中的测试结果可以看出，与PCA方法相比，本文方法对自测数据的5个被试的运动想象同样具有较高的识别率和稳定性。

4 结束语

本文介绍了一种基于贝叶斯网络建模的运动想象脑电信号判别分析方法，并说明该方法的原理及流程。通过使用高斯分布来充分描述出脑电数据的分布特征，进而得到各个导联之间相互关系，同时，将电极之间的物理关系作为限制条件构建贝叶斯网络。

通过对比本文方法与PCA+fisherscore方法对2组实验数据的识别效果，表明本文方法具有较好的识别效果。然而对于分布非平稳且不规则的脑电数据而言，用单高斯模型去描述脑电数据的分布特征仍然可能会丢失很多重要信息。因此，下一步的工作主要集中在如何更全面、完整地描述脑电数据的分布特征，进而构建相应的贝叶斯网络。

[1]万 柏,綦宏志,赵 丽.基于脑电Alpha波的脑-机接口控制实验[J].天津大学学报,2006,39(8):977-983.

[2]Krusienski D J,McFarland D J,Wolpaw J R.An Evaluation of Autoregressive Spectral Estimation Model Order for Braincomputer Interface Applications[C]//Proceedings of IEEE EMBS Annual International Conference.New York,USA:IEEE Press,2006:1323-1326.

[3]廖 样,尹 愚,尧德中.基于连续小波变换和支持向量机的手动想象脑电分类[J].中国医学物理学杂志,2006,23(2):129-132.

[4]Adeli H,Zhou Ziqin,Dadmehr N.Analysis of EEG Records in an Epileptic Patient Using Wavelet Transform[J].Journal of Neuroscience Methods,2003,123(1):69-87.

[5]Pfurtscheller G,Kalcher J,Neuper C.On-line EEG Classification During Externally-paced Hand Movements Using a Neural Network-based Classifier[J].Electroencephalography and Clinical Neurophysiology,1996,99(5):416-425.

[6]Cooper G F,Herskovits E.A Bayesian Method for the Induction of Probabilistic Networks from Data[J].Machine Learning,1992,9(4):309-347.

[7]刘志强.因果关系,贝叶斯网络与认知图[J].自动化学报,2001,27(4):552-566.

[8]Yang Guosheng,Lin Yingzi,Bhattacharya P.A Driver Fatigue Recognition Model Based on Information Fusion and Dynamic Bayesian Network[J].Information Sciences,2010,180(10):1942-1954.

[9]Ko K E,Yang H C,Sim K B.Emotion Recognition Using EEG Signals with Relative Power Values and Bayesian Network[J].International Journal of Control,Automation and Systems,2009,7(5):865-870.

[10]Li Xiangyang,Ji Qiang.Active Affective State Detection and User Assistance with Dynamic Bayesian Networks[J].IEEE Transactions on Systems,Man and Cybernetics,2005,35(1):93-105.

[11]张剑飞,王 辉,周颜军,等.基于局部优化具有连续变量的贝叶斯网络结构学习[J].东北师大学报:自然科学版,2006,38(1):27-30.

[12]Jie Cheng,Bell D,Liu Weiru.Learning Bayesian Networks from Data:An Efficient Approach Based on Information Theory[J].Artificial Intelligence,2002,137(1/2):43-90.

[13]Wong M L,Leung K S.An Efficient Data Mining Method for Learning Bayesian Networks Using an Evolutionary Algorithm based Hybrid Approach[J].IEEE Transactions on Evolutionary Computation,2004,8(4):378-404.

[14]Neapolitan R E.Learning Bayesian Networks[M].New York,USA:Prentice Hall,2003.

[15]王书海,刘 刚.BIC评分贝叶斯网络模型及其应用[J].计算机工程,2008,34(15):229-230,233.

[16]叶 坤.左右手运动想象脑电采集和特征提取方法初探[D].武汉:华中科技大学,2008.

[17]穆振东,胡剑锋,肖 丹.基于时频域分析的运动想象脑电信号分类[J].中国组织工程研究与临床康复,2009,13(26):5079-5082.

[18]Cao Lei,Li Jie,Sun Yaoru,et al.EEG-based Vigilance Analysis by Using Fisher Score and PCA Algorithm[C]//Proceedings of IEEE International Conference on Progress in Informaticsand Computing.[S.l.]:IEEE Press,2010:175-179.