用于导航解算的矩阵运算硬件加速器设计

马邺晨，李醒飞

(天津大学精密测试技术及仪器国家重点实验室，天津 300072)

1 概述

作为惯导系统核心环节，导航解算的实时性决定着惯导系统能否及时跟踪运载体的运动［1］。导航解算从计算颗粒划分，主要包括向量加法、三维向量叉乘、四元数乘法、矩阵-矢量积和矩阵乘法5种运算，其中，矩阵乘积计算量大，耗时也最多［2］。从解算流程划分，载体坐标系旋转更新模块，姿态、速度、位置更新模块中均包含一次或多次矩阵乘法，初始对准中采用的滤波器算法也包含大量的矩阵乘法运算［3］。因此，提高浮点矩阵乘法运算速度对惯导系统实时性的提高具有重要意义。

之前的浮点矩阵乘积运算一般都采用PC或DSP实现，但这种串行处理器在应对高阶数、高复杂度的算法时，更新速率并不高。伴随超大规模集成电路技术的发展，国内外很多学者开始研究使用具有并行处理能力的FPGA来计算浮点矩阵乘积［4］。文献［5］提出了一种各计算单元之间不存在任何通讯的并行矩阵乘法器结构，但其所需要的存储空间随矩阵维数的增加而显著增加，且效率较低。文献［6］在Xilinx FPGA上设计了用于双精度浮点矩阵乘法的处理单元(Process Element，PE)阵列结构，峰值计算性能可达到3 GFLOPS，但其并未采取任何运算优化措施，且计算性能随矩阵维数增加而下降。文献［7］基于Nios II系统，应用浮点运算宏功能模块设计了矩阵硬件加速器，但并未探究其加速机理;另外虽然该方法总体消耗的周期数较串行方法有所下降，但部分环节效率依旧较低。

针对上述问题，本文分析了FPGA浮点矩阵乘积运算加速原理，包括经典脉动阵列结构并行提速以及近两年新提出的用于增强矩阵处理并行度的数据空间、迭代空间处理方法。基于上述原理，编写出高性能浮点矩阵乘积模块，用于提高计算速度;在数据交换方面，摒弃传统传输模式，利用DMA大批量高速传输速度优势进行数据交换，从而设计出性能良好的浮点矩阵乘积加速器。最后利用嵌入式逻辑分析仪SignalTap II对运算过程进行性能实测。

2 FPGA浮点矩阵乘积加速原理

2.1 计算单元阵列结构

矩阵乘法作为操作次数大于输入输出象元的运算，属于计算受限类型。常采用具有并行-流水线特点的脉动(systolic)阵列［8］实现并行计算。该阵列由功能相同或相近的PE组成，运算中数据受同一个时钟控制，在各PE间沿着预设的方向流动，在数据流流入、流出阵列的过程中完成运算。以 Cm×n=Am×p×Bp×n为例，m 个 PE 串联而成的一维 systolic线阵运算过程如下:B阵中的数据按照行序串行流过阵列中每一个PE单元，同时A阵形成m条数据流分别输入相应的单元，在每n个周期内保持恒定，以列序p循环。2个数据在PE中相遇进行相应运算，并把形成的部分结果存放在加法循环回路中，这样当B阵传输结束时，各PE元分别输出结果矩阵各行计算结果。

与微处理器串行实现方法2×m×p×n，即ο(n3)的计算复杂性相比，采用一维systolic线性阵列结构，计算的复杂性降低至2×p×n，即ο(n2/m)。矩阵运算时空映射而得出的二维脉动阵列能将矩阵计算的复杂性降至ο(n2/mp)。

2.2 分块映射策略

应对不同规模的矩阵，尤其针对较大矩阵，简单依赖增大阵列规模，以资源换速度的计算方法会受到片上资源约束，因而需将大规模问题映射到较小或(固定)规模的阵列上。现今常用的映射方法是循环分块［9］，即以局部并行、全局串行的方式完成调度。其核心思想是:将计算过程分为2层循环，内层并行完成矩阵运算，外层通过有限状态机完成过程控制、外部存储器与计算阵列之间的数据传输。

针对循环中大批量的数据访问，对数据空间分割及迭代空间合并是增加访问并行度的有效手段［10］。其思路是:通过建模获取循环控制流下访存密集数组的访问形式及相关性，若迭代空间中矩阵数目大于1，且未遇到新矩阵，则依照迭代空间维度顺序由内向外将所有数据空间内矩阵分为(N×所需宽度)个矩阵。为不失分块后矩阵间相关性，再合并迭代空间，合并过程减少了循环次数，因而状态机跳转次数也降低，循环迭代过程所占的延时降低。以A×B，分块数4为例，处理前后的数据访问为:

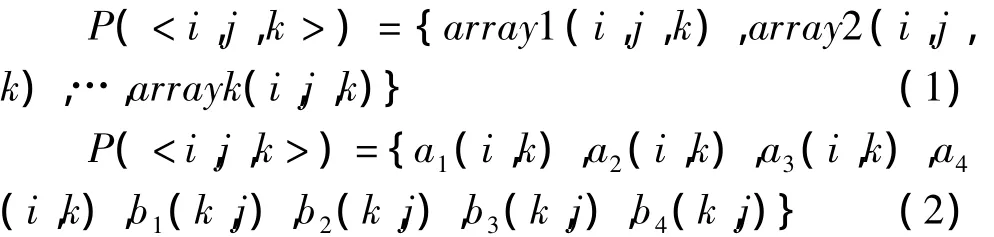
其中，array分别为矩阵A，B的行、列向量;a1～ a4，b1～b4分别为矩阵A，B分块后的子矩阵。

数据空间和迭代空间经优化后，设处理器空间的PE单元数为Sp，矩阵A和B存储模块深度为St1，St2。此时加载矩阵A，B，加载并存储结果矩阵C带来的数据传输量分别为:

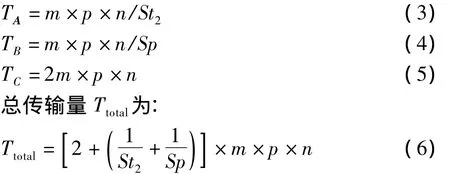
可见St1的大小对数据传输量没有影响，故不考虑其他因素时可将St1设为1，即让A矩阵的存储模块退化为寄存器，给St2留更多余量，可增大其值以进一步减少数据传输耗时，提高运算速度。

3 浮点矩阵乘积加速器设计

基于多处理器核FPGA/SOPC的导航解算以解算模块流水线化、模块内各粒度计算单元同时进行的方式［7］完成解算任务。处理器调度各运算单元完成操作数的读取、运算、结果存储。

对于完成浮点矩阵乘积的运算单元，其任务可分为矩阵计算和对缓冲区数据访问两部分。上述两方面着手提升运算速度，据此设计的加速器总体结构如图1所示。作为导航解算中的协处理器，加速器采用硬件方法完成复杂耗时的矩阵乘积运算，同时还可以通过Avalon-MM总线与导航系统中其他模块通信。

各模块设计说明如下:

(1)浮点矩阵乘积模块:基于浮点矩阵乘积加速原理制成的浮点矩阵乘积单元由矩阵A，B存储模块、寄存器、高速缓存器、高性能点乘、求和计算单元5个部分组成。其结构如图2所示。

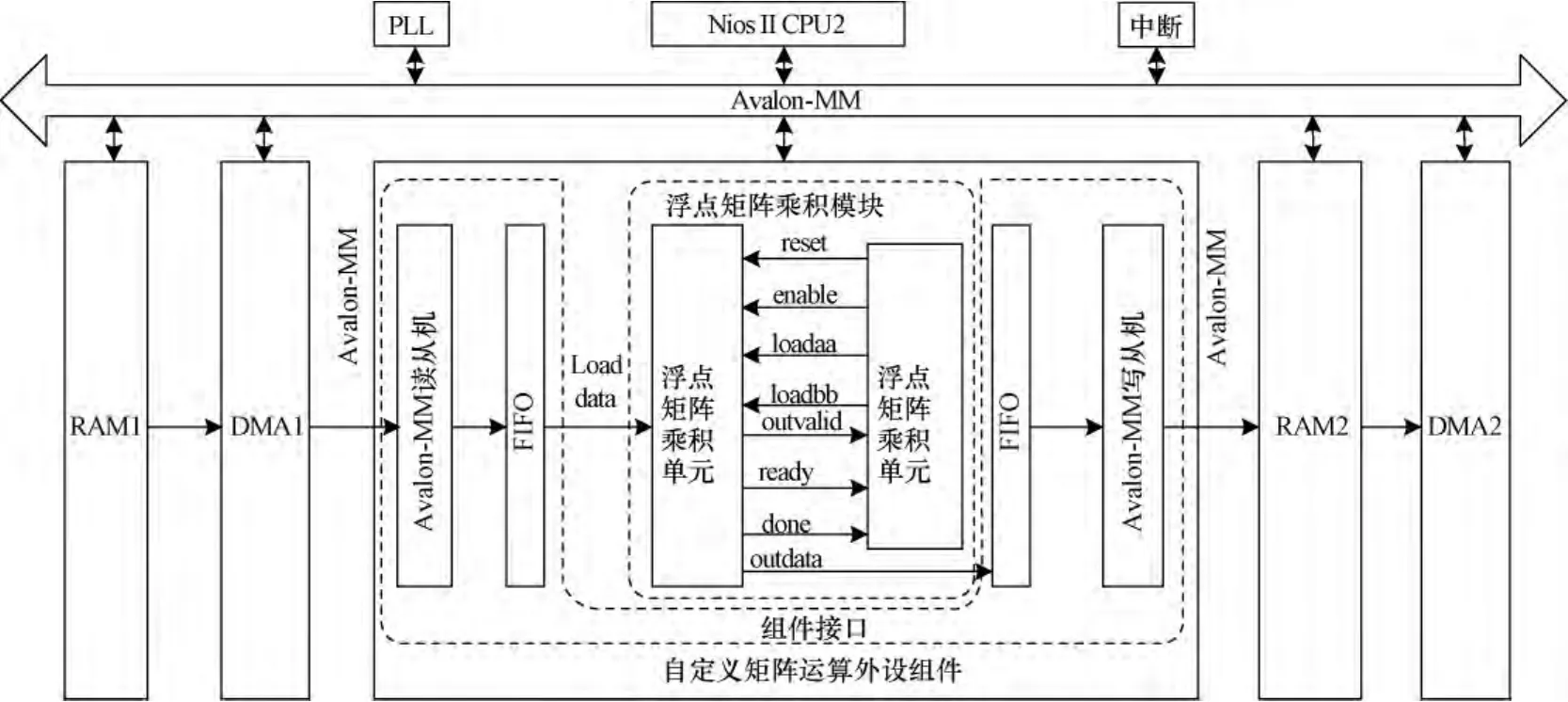
图1 浮点矩阵乘积加速器总体结构

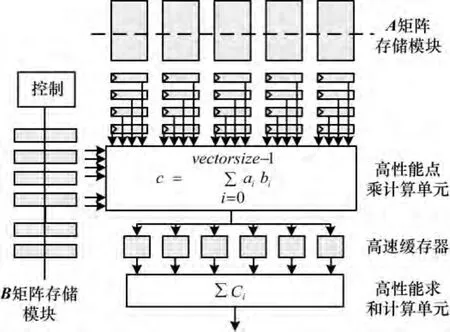
图2 浮点矩阵乘法单元结构

应用中，依据数据空间分割及迭代空间合并理论选择矩阵分块参数vectorsize，block的最优值。矩阵乘法宏功能模块据此参数生成相应规模的DSP block二维阵列完成点乘计算。阵列中DSP block完成18×18乘积和运算并兼具高频流水线、反馈累加与级联功能，使得内层迭代仅耗(vectorsize/(2×block))个时钟周期，再经(A矩阵的列数/vectorsize)次迭代运算，高性能求和计算单元将中间量对应相加，得到结果矩阵C。另外优化为部分寄存器的A矩阵存储模块由M144K充当，相比B矩阵带宽较窄，使用中需要在A当地寄存器中存放多个数据以拓展带宽，使数据加载用时不超过处理耗时，达到较高的占空比。

加速器中设定矩阵分块参数，例化生成的硬件描述语言文件，再根据时序图将运算过程划分为数据加载、运算开启、运算处理、结果输出4个状态，编写状态机控制乘积单元运算，完成浮点矩阵乘积运算。

(2)DMA［11］:FPGA/SOPC 平台上传统的Avalon-MM(Avalon Memory Mapped Interface)总线数据传输方式基于地址映射方式，控制信号繁多，尤其在大批量数据传输时，CPU中断载荷负担重，导致传输速率较低。但同样采用Avalon-MM总线的DMA以单向点对点方式传输，用精简的控制方式及高速流模式进行数据传输，不会影响CPU的其他工作。大批量数据传输时具有非常高的传输效率。

SOPC中DMA数据传输依赖于硬件系统搭建和DMA控制器控制。加速器硬件系统需配置处理器、PLL、DMA、外部存储控制器等组件，设置DMA长度寄存器位宽、构建方式、基址和中断级，连接读写主端口与源、目的地址所在的组件。控制方式采用为Nios II系统提供设备驱动程序的HAL库中功能语句，而非寄存器方式。

(3)组件接口:浮点矩阵乘积模块只有添加MM总线读写从机并进行封装后才能被Nios II系统调用，另外DMA传输单个浮点数用时不恒定，而矩阵乘积运算的数据加载要求字加载速度恒定在一个时钟周期，这样就出现数据传送速率不匹配。故在编写MM读写从机程序的基础上采用FIFO实现数据传输与加载间的同步。使用存储器处理跨域传输，避免了握手信号和逻辑同步处理机制在同步设计中大量的时钟周期消耗，保证了通信双方较高的数据吞吐率。设计中编写 FIFO读写时序，使得FIFO能在DMA数据线上数据正确时将其读入，当FIFO中暂存的数据量达到指定数目后，再依照加载时序读出，实现数据传输与加载间的同步。

浮点矩阵乘积加速器硬件系统设计完成后，进行软件部分设计。软件部分任务是控制DMA实现RAM与自定义外设之间的流模式数据传输。为保证计算结果的及时输出，注册PIO中断标志量，使其在浮点矩阵乘积模块计算结果有效时置1，并在中断服务子程序中完成DMA2到RAM2之间的数据输送。系统主程序流程如图3所示。

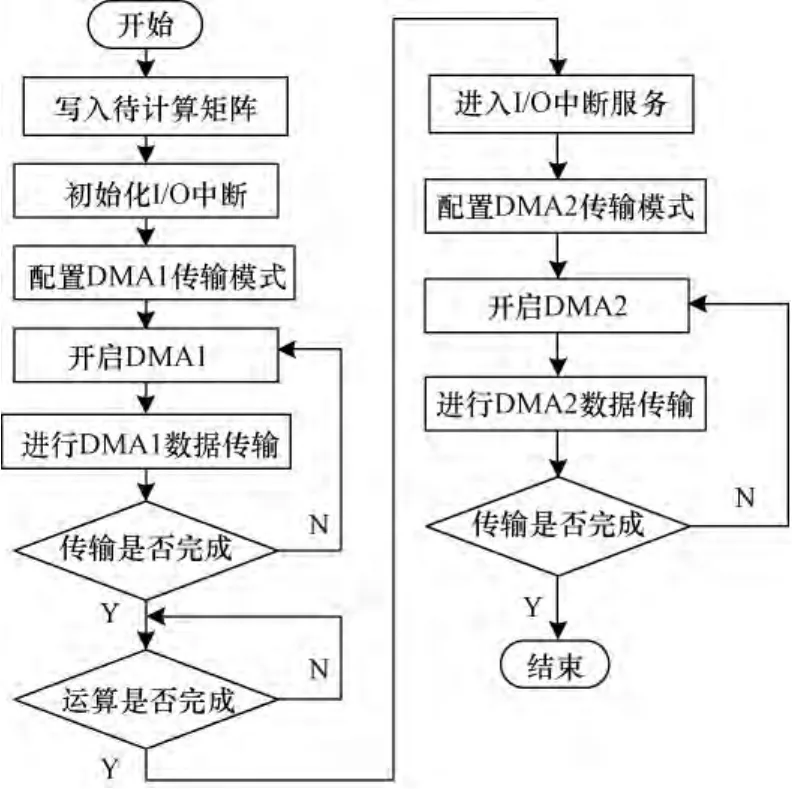
图3 系统主程序流程

4 实验分析

4.1 浮点矩阵乘积模块功能测试

本文以非方阵乘积 A10×8×B8×12为例，对浮点矩阵乘积模块进行功能仿真测试。选取A，B矩阵vectorsize=8，blocksize=2，testbench 脚本中时钟信号200 MHz，在Modelsim_altera平台上进行仿真。仿真测试结果如图4所示。

图4中整个运算过程消耗了1885 ns，即377个时钟周期。浮点操作数表达式为:

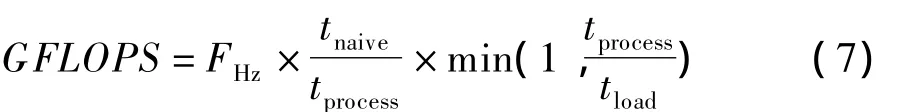
其中，FHz表示系统运行频率;tload，tprocess，tnaive分别表示数据加载、处理、简单算法时间。依据上述公式及仿真结果得出:时钟信号200 MHz时浮点矩阵乘积模块的浮点操作数达到了2.09 GFLOPS。由于浮点矩阵乘积单元的峰值频率可以达到412 MHz［12］，因此峰值计算性能可达到4.30 GFLOPS。

使用浮点矩阵乘积模块与在PC上使用Matlab计算矩阵乘积的部分结果对比如表1所示。从运算结果可以看出，浮点矩阵乘积模块可以正确完成乘积计算。只是乘积模块直接计算单精度浮点数，而Matlab中间过程以双精度形式进行，结果转换为单精度形式输出，从而导致了结果的微小差异。

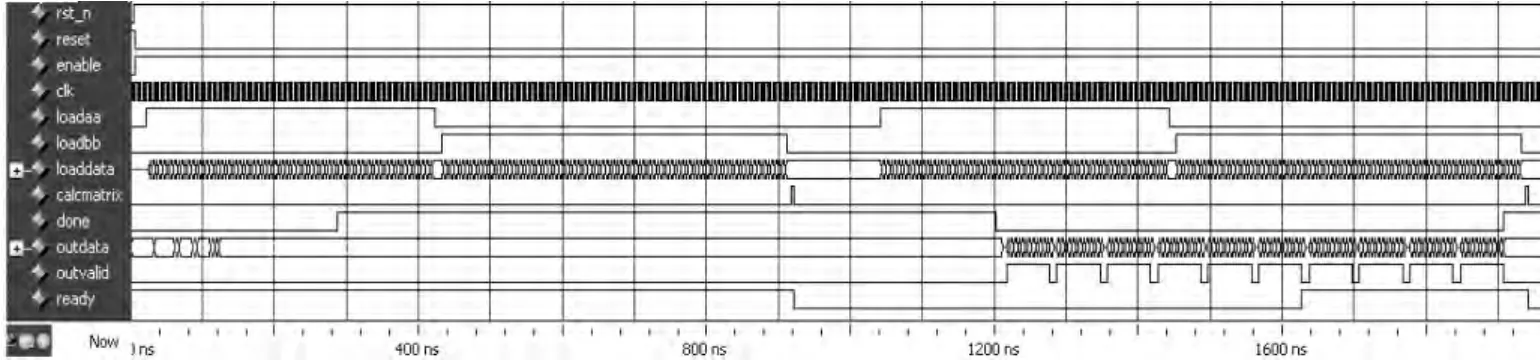
图4 Modelsim仿真测试结果

表1 部分运算结果对照

4.2 浮点矩阵乘积加速器性能实测

将浮点矩阵乘积加速器的.sof文件下载至Altera DE3开发板，在Nios EDA平台上以硬件方式运行软件程序，使用嵌入式逻辑分析仪SignalTap II对浮点矩阵乘积加速器的计算性能进行测试，选取CPU的时钟信号作为采集时钟，实时采集得到的信号如图5所示。由实测图可以看出，浮点矩阵乘积加速器计算时序与功能测试吻合。从数据读取、矩阵运算到结果输出一共消耗了842个时钟周期。在200 MHz时钟实验条件下，耗时4.21 μs。各种浮点矩阵乘积方法的性能分析如表2所示，本文方法较其他文献中硬、软件实现方法速度分别提升71.3%，78%。

图5 SignalTap II实测图

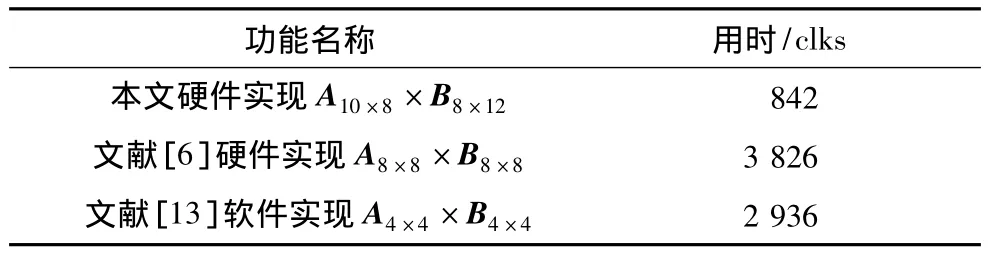
表2 浮点矩阵乘积方法的性能分析

5 结束语

为提高导航解算中矩阵乘积运算速度，本文从硬件实现角度设计了应用于Nios II系统的矩阵运算加速器。首先分析了FPGA用于浮点矩阵运算的加速原理，据此编写性能优越的矩阵乘积模块并使用Modelsim进行功能仿真验证。之后设计DMA传输通道及外设，并将整体封装成自定义组件作为Nios II系统的协处理器。为验证其实际特性，将所有程序下载至Altera DE3开发板进行实测，利用SignalTap II拾取的信号与其他实现方法对比表明，本文设计的矩阵运算硬件加法器具有明显的速度优势，有利于提高导航解算的实时性。

［1］秦永元.惯性导航［M］.北京:科学出版社，2006.

［2］林灿龙，马龙华，吴铁军，等.高动态条件下的捷连惯导并行算法研究［J］.弹箭与制导学报，2012，32(2):1-5.

［3］李宗涛.高动态捷连惯导系统的并行实现分析［D］.杭州:浙江大学，2011.

［4］Underwood K.FPGAsvs.CPUs:Trendsin Peak Floating-point Performance［C］//Proc.of International Symposium on Field Programmable Gate Arrays.Monterey，USA:ACM Press，2004:171-180.

［5］Campbell S J，Khatri S P.Resource and Delay Efficient Matrix Multiplication Using NewerFPGA Devices［C］//Proc.of the 16th ACM Great Lakes Symposium onVLSI.Philadelphia，USA:ACM Press，2006:308-311.

［6］田 翔，周 凡，程耀武，等.基于FPGA的实时双精度浮点矩阵乘法器设计［J］.浙江大学学报:工学版，2008，42(9):1611-1615.

［7］许 芳，席 毅，陈 虹，等.基于 FPGA/Nios-II的矩阵运算硬件加速器设计［J］.电子测量与仪器学报，2011，25(4):377-382.

［8］Dutta H，HannigF，Ruckdeschel H，et al.Efficient Control Generation for Mapping Nested Loop Programs onto Processor Arrays［J］.Journal of Systems Architecture，2007，53(5):300-309.

［9］Wolfe M J，Shanklin C，Ortega L.High Performance Compilers for Parallel Computing［M］.Boston，USA:Addison-Wesley Longman Publishing Co.，Inc.，1995.

［10］Asher Y，Rotem N.Automatic Memory Partitioning:Increasing Memory Parallelism via Data Structure Partitioning［C］//Proc.of International Conference on Hardware/Software Codesign and System Synthesis.Scottsdale，USA:IEEE Press，2010:155-161.

［11］Altera Corporation.ALTERA Embedded Peripherals IP User Guide［EB/OL］.(2011-06-10).http://www.altera.com.cn/literature/ug/ug_embedded_ip.pdf.

［12］Altera Corporation.ALTERA Floating-point Megafunctions User Guide ［EB/OL］.(2011-06-10).http://www.altera.com.cn/literature/ug/ug_altfp_mfug.pdf.

［13］雷 晶，金心宇，王 锐.矩阵相乘的并行计算及其DSP 实现［J］.传感技术学报，2006，19(3):737-740.