最小化多MapReduce任务总完工时间的分析模型及其应用＊

田文洪，陈 瑜，王心阳，薛瑞尼，赵 勇

（1.电子科技大学信息与软件工程学院，四川 成都 610054；2.电子科技大学计算机科学与工程学院，四川 成都 611731）

1 引言

在云计算和大数据处理时代，MapReduce的开源实现Hadoop以其通用性和方便实用等特征得到了迄今为止最为广泛的应用。在云计算研究中，MapReduce环境的作业调度带来了一个新的课题和挑战，引起了越来越多的重视。最初，Hadoop默认的FIFO（先入先出）调度器是专为周期性执行大规模批量作业而设计的。随着MapReduce集群的用户数量的增加，计算能力调度器［1］和Hadoop公平调度器HFS（Hadoop Fair Scheduling）［2］的出现，提供了更高效的集群共享方式。业界已有少数研究Hadoop的调度原型的研究小组，旨在优化一些明确给定的调度标准，例如FLEX［3］、ARIA［4］。MapReduce的模拟器SimMR［5］也被开发出用于模拟不同的工作量下MapReduce的性能。但是，正如文献［6］中指出的，现有的调度器还不能提供对最小化作业集完工时间的支持。Tian等［7］针对离线多任务调度提出了几种高效的最小化总完工时间的调度算法并进行了对比分析，文献［8］针对在线多任务节能调度提出了一种高效动态划分算法，以最小化总完工时间。Tian等［9］提出了一种云数据中心动态负载均衡调度算法，该算法同时考虑CPU内存和网络带宽的利用率。

Herodotou H等［10］提出了一种工作流－感知调度器，通过把数据位置与任务调度相结合，优化工作流完工时间。Moseley B等［11］将MapReduce调度转化为经典的具有相同机器的两阶段工作车间作业问题，在离线情况下，他们提出了一个对于最小化总完成时间近似比为12的近似算法。文献［6，12］提出了一种通过在Hadoop集群中创建两个资源池（pools）的启发式算法—BalancedPools算法，以负载均衡并最小化任务的总完工时间。该算法当任务请求的资源低于系统可提供的最大资源时不进行动态资源分配调整，而是运行多个任务共享系统资源，因而不满足经典Johnson算法的条件。经典Johnson算法［13］要求一个物品必须通过一个生产阶段（或者一个机器），然后通过第二个阶段，每个阶段只有一个机器，一个机器上任何时刻一次最多处理一个物品，在此种情况下可以利用经典Johnson算法安排出一批任务的执行顺序，并计算出最小总完工时间。

本文总结已有研究成果的优缺点，旨在将MapReduce两阶段与经典Johnson算法的两阶段条件完全匹配，从而利用Johnson算法计算出一批任务的最小总完工时间，并应用于集群节能、负载均衡等问题。

2 问题描述与建模

定义1 MapReduce时隙（MapReduce slots），是指在给定的一个Hadoop集群中，其总的MapReduce资源时隙，本文与文献［5］一样，设定一个Hadoop集群节点同时具有一个MapReduce slot，例如一个Hadoop集群具有60个节点，可以表示其总的MapReduce slots为60×60。当然这也可以依据具体情况动态设定。

定义2 一个作业在一个给定Hadoop集群中的执行次数，用waves来表示，例如一个任务请求使用30个Map slots和30个Reduce slots，在一个具有20×20MapReduce slots的Hadoop集群，其执行Map阶段的waves为2，其执行Reduce阶段的waves为2，其它的类推。图1展示了一个MapReduce wordcount运行的例子。

Figure 1 An execution example in 20×20MapReduce slots图1 一个在20×20MapReduce slots执行的例子

定义3 一批任务在Hadoop集群中的总完工时间（Total Makespan），是指按照一定的顺序执行完该批任务的所有Map／Reduce阶段从第一个任务Map阶段开始到最后一个任务Reduce结束所花的总时间。

文献［4，6，12］介绍了一个Map／Reduce性能模型。该模型可通过输入数据大小和分配资源作为函数的参数，预测Map和Reduce阶段的完工时间。考虑一个由n个任务组成的作业，在k个MapReduce的slots中执行的Hadoop环境，任务安排在slots中执行时采用离线贪心算法：每次选择完工时间最早的任务安排。设avg和max分别为n个任务的平均时间和最大时间，则在贪心算法下，作业的总完工时间最少为n×avg／k，最多为（n－1）×avg／k＋max，每个作业由特定数量的Map和Reduce任务组成。该作业的执行时间和具体的执行依赖于分配所得的资源量（Map slots和Reduce slots）。我们采用文献［6］中的一个简单抽象，将一个MapReduce作业Ji的Map和Reduce过程定义为mi和ri，即Ji＝（mi，ri），对于任何两个独立的MapReduce作业J1和J2，这两个作业之间没有数据依赖关系。只有当第一个作业完成Map阶段并开始Reduce阶段的处理时，第二个作业才可以开始使用释放的资源来执行Map，参见图3。下一个作业的Map阶段可能会与前一个作业的Reduce阶段在时间上“重叠”（Overlapped）。我们进一步考虑以下问题：设J＝｛J1，J2，…，Jn｝是一个n个数据相互独立的MapReduce作业。Ji需要Ni×Nr个MapReduce slots，Map和Reduce的时间分别是（mi，ri），系统调度器依据可用资源可以改变一个作业的MapReduce slots分配。假设T是所有n个作业的总完工时间，我们的目标是对于Ji∈J确定一个顺序，使得所有作业的总完工时间最小。我们假设一个作业Ji，其Map结束时间和Reduce开始时间分别为，实际分配的MapReduce slots为Pi×Pi，而Hadoop集群中最大的MapReduce slots为P×P。因此，最小化总完工时间问题可以表示如下：

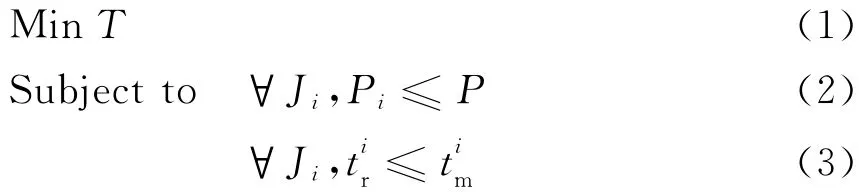
其中，不等式（2）由可用资源限定，实际分配的资源（Pi）不能超过系统可用资源（P）；不等式（3）由单个作业Map和Reduce过程不能重叠限定，对于任何一个作业，其Reduce开始时间不应比其Map的完工时间早。

3 最小化总完工时间问题解决方案：更新的经典Johnson算法

经典Johnson算法［13］描述有n个物品必须通过一个生产阶段（或者一个机器），然后通过第二个阶段，每个阶段只有一个机器，一个机器上任何时刻一次最多处理一个物品。为了让其能够用于MapReduce模型，我们将Map和Reduce阶段的资源看做一个整体，来表示MapReduce的slots资源。然后我们可以使用Johnson算法，考虑一个n个作业的集合，每个作业使用一个用Map和Reduce时间组成的数据（mi，ri）表示，每一个作业Ji＝（mi，ri）的属性Ai定义如下：

Ai的第一个参数称为持续时间，表示为A1；第二个称为阶段类型（Map或Reduce），表示为A2。注意到如果当所有的ri＝0时，Johnson算法简化为短作业优先算法（SPT），该算法是已知的可用于找到所有作业最小总完成时间的最优值的方法。MapReduce改进的Johnson算法的伪代码如下所示：

算法1 改进的Johnson算法

输入 所有作业的Map和Reduce阶段的持续时间mi、ri，Hadoop集群的机器数量，系统Map／Reduce slots总数P。

输出 所有调度任务的安排顺序和这批任务总的完工时间。

步骤1 将所有任务的Map和Reduce阶段的持续时间列出；

步骤2 对于所有持续时间；

步骤3 找出其最短者；

步骤4 若出现多个最短者相同的情况，则按任务编号顺序处理。

步骤5 若Map阶段与Reduce阶段持续时间相同，则优先考虑为Map类型；

步骤6 若任务类型为Map型，则置于第一个位置处理；

步骤7 否则任务类型为Reduce型，则置于最后一个位置处理；

步骤8 移除已经分配的任务；

步骤9 对剩余的任务重复步骤3～步骤8，直到所有任务分配完。

首先将在作业J中的n个作业按照下列方式排 序：Ji在Ji＋1之 前 当 且 仅 当min（mi，ri）≤min（mi＋1，ri＋1）。它寻 找 的 是 持 续 时 间 最 短 的 作业，如果阶段类型Ai是m，它代表Map类型，则Ji被放置在调度表头，否则Ji被放置在尾部。然后移除Ji，对剩下的作业采取同样操作直到所有作业分配完。Johnson算法的时间复杂度主要在于排序n个任务，因而是O（nlogn）。

定理1 在两阶段生产系统中，如果所有作业经历相同阶段，且任何时刻任何一个阶段的资源只能由一个任务占用，则Johnson算法可以获得系统总完工时间的最小值。

该定理的详细证明参考文献［13］。

使用Johnson算法我们可以通过如下方式计算出系统最小总完工时间。考虑有Map和Reduce阶段的n个任务，设在给定的有P个节点的Hadoop集群中，mi为第i个任务Map阶段持续时间，ri为Reduce阶段的持续时间，则系统的最小总完工时间为：

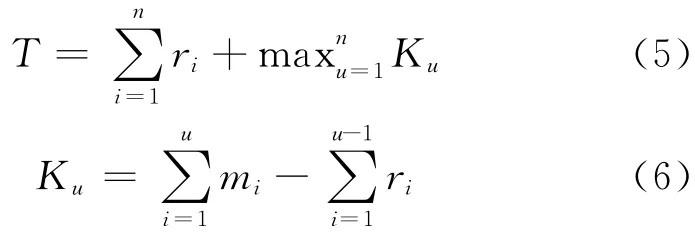
观察结果1 如果每个工作能够完全利用Map或者Reduce过程中的slots，那么MapReduce作业的处理可与经典Johnson算法的两阶段生产系统完全匹配，则Johnson算法就可用来寻找所有MapReduce作业的最小总完工时间的最优解。

例1 在文献［2］中给定的五个MapReduce作业例子，我们重新绘制如图2所示。

Figure 2 Example of five MapReduce jobs图2 五个MapReduce作业例子

图2a为五个作业Map和Reduce阶段的持续时间列表，图2b为五个作业使用Johnson算法由排序后的执行顺序。根据Johnson算法，最优顺序为δ＝（2，5，1，3，4），由式（6）可计算出，此序列的总延迟时间为4个单位时间，总完工时间是47个单位时间（由式（5）计算出）。如果将此序列翻转，即（4，3，1，5，2），则得到最坏的结果（上限），为78个单位时间。

观察结果2 假设当作业要求分配MapReduce的slots比系统可用的MapReduce的slots少，系统调度器不给MapReduce增加slots；同时，每一个阶段若允许两个或两个以上的作业共享slots，例如文献［6］所介绍的方法则违反了Johnson算法要求任何时刻在机器上只能有一个作业在执行的条件。

图3和图4分别给出了一个不满足和满足Johnson算法条件的任务执行情况。

例2 让作业J1、J2和J5请求30个Map和30个Reduce slots任务，作业J3和J4请求20个Map和20个Reduce slots任务。图3展示了这五个MapReduce作业依据Johnson算法的执行顺序δ＝（J2，J5，J1，J4，J3）的 执 行 过 程。当 可 用 的MapReduce的slots的数量比请求的MapReduce slots的数量大的时候，如果我们不把作业分为两个池，同时不增加slots的数量为系统最大可用值（如J3和J4需要20×20个slots而系统作为整体有30×30个slots），如图3所示，使用Johnson算法，调度总共的完工时间（Makespan）是44个单位，这比通过文献［6］中两个池的方法得到的结果（40）大了10%。注意到，J4用20×20个slots，Map和Reduce阶段分别有6和30个单位的持续时间；J3的Map阶段在时间段［7，13］使用10个Map slots与J4共享系统资源，在时间段［13，40］使用20个Map slots继续执行，然后J3的Reduce阶段在时刻40开始，在时刻44结束。

观察结果3 作业的阶段持续时间取决于分配资源的数量（Map和Reduce的slots）。若系统调度分配MapReduce slots的数量不同，作业运行的总时间就可能不同。

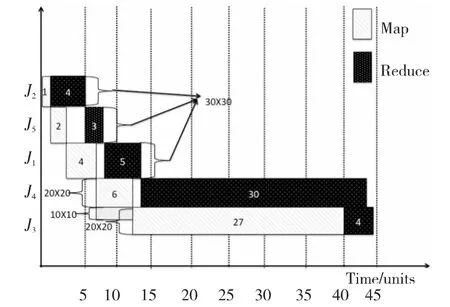
Figure 3 Execution result of five MapReduce jobs（not using max available slots）图3 五个MapReduce作业在一个集群中执行

例3 考虑在文献［6］中的情景2：作业J1、J2和J5申请30个Map和30个Reduce slots，作业J3和J4申请20个Map和20个Reduce slots，且J3＝（m3，r3）＝（30，4），J4＝（6，30）。我们在图3中展示了这五个MapReduce作业根据生成的Johnson调度顺序δ＝（J2，J5，J1，J4，J3）的执行过程。对于作业J3和J4，文献［6］假设即使系统中有30×30个MapReduce slots可用的情况下，他们只用了20×20个MapReduce slots。然而，如果我们允许作业可以使用系统中所有可用的MapReduce slots来执行（这在Hadoop中很容易实现，如将大的输入文件基于可用的MapReduce slots数量进行分片），得出的结果和文献［1］中得出的很不相同。使用在文献［1］的情景2中的同样示例，则现在作业J3和J4可以使用所有可用的30×30个MapReduce slots，那么J3将有Map和Reduce的持续时间分别为（20，8／3），J4将有Map和Reduce的持续时间分别为（4，20），它们都比使用20×20个MapReduce slots用时少，如图4所示的执行结果。因此，总的Makespan将为其中X1＝1。这个结果比通过两个池［2］所得结果要小约12%。

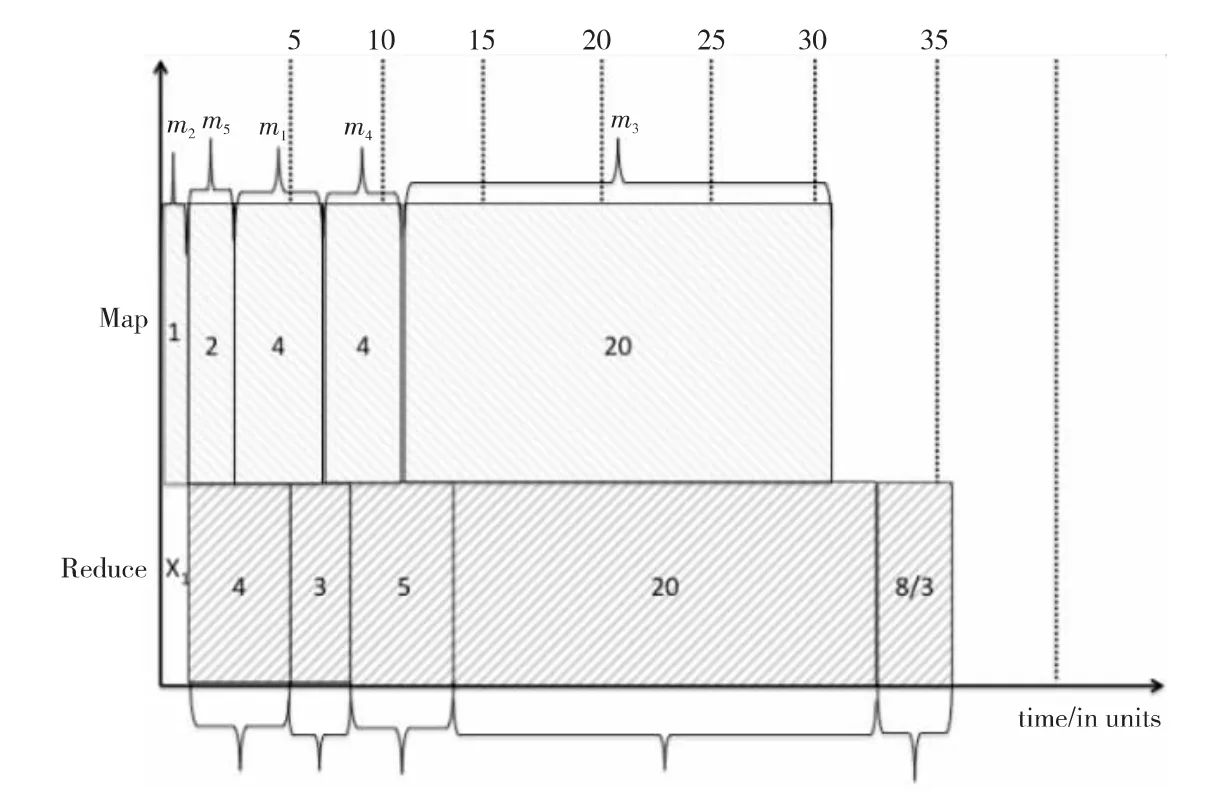
Figure 4 Execution result of five MapReduce jobs（using max available slots）图4 五个MapReduce作业在一个集群中执行（利用系统最大资源满足经典Johnson算法条件）

引理1 如果作业请求的MapReduceslots数量比系统中总的可用MapReduceslot数量多或少，调度系统可以减少或者增加分配给作业的MapReduceslots数量，以最大限度利用Hadoop资源，从而最小化系统总完工时间。

证明 这一动态调整满足了经典Johnson算法两个阶段的执行条件，即任何时刻任何一个阶段的资源只能由一个任务占用，所以我们可以使用经典Johnson算法来安排任务执行顺序，并使用公式（5）～公式（6）计算出系统最小总完工时间。□

算法2依据引理1的动态分配系统MapReduce slots资源方法的伪代码如下所示：

算法2 动态MapReduce slots分配方法

输入 所有作业的Map和Reduce阶段的持续时间mi，ri，Hadoop集群的机器数量，系统MapReduce slots总数P。

输出 所有作业实际分配的MapReduce slots。

步骤1 将所有任务的Map和Reduce阶段的持续时间列出；

步骤2 对于所有作业请求的MapReduce slots；

步骤3 若作业请求的slots与系统可分配的最大slots相同，则分配给其最大slots；

步骤4 若作业请求的slots大于系统可分配的最大slots，则按照系统可分配的最大slots分配（将大的输入文件基于可用的MapReduce slots数量进行分片后执行多个waves），并重新计算其各阶段的持续时间；

步骤5 若作业请求的slots小于系统可分配的最大slots，则按照系统可分配的最大slots分配（将大的输入文件基于可用的MapReduce slots数量进行分片），并重新计算其各阶段的持续时间；

步骤6 将新的结果提交调度系统使用。

4 最小化多MapReduce任务总完工时间应用于Hadoop集群节能

利用前述结果，可以在调度系统设计时优化多任务的总完工时间，从而提高响应速度和服务质量。利用前述结果和能耗模型，我们还可以建立集群总能耗与多任务总完工时间的关系，从而进行能耗优化设计。考虑CPU为主的能耗模型，一个节点一段时间内的能耗可以表示如下［14，15］：

本文考虑Hadoop集群节点同构的情况，其中Pi为Hadoop集群节点i（一个服务器）的功率，Pmin是节点的利用率为0时的功率，Pmax是节点利用率为100%时的功率，Ui为节点CPU的平均利用率。

节点i在一段时间［t0，t1］内的总能耗Ei可表示为：

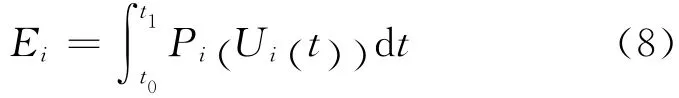
其中，Pi（Ui（t））为功率函数；而Ui（t）为CPU在时刻t的利用率，若使用一段时间Ti（＝t1－t0）内的平均利用率，则公式（8）可以简化为：

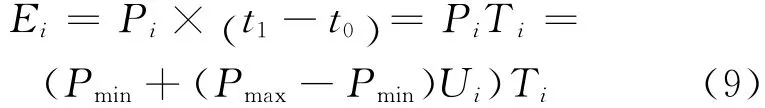
则一段时间内的Hadoop集群的总能耗可表示为：

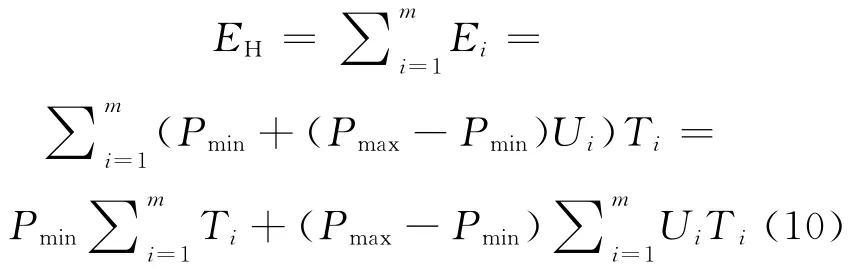
其中，m为Hadoop集群中的节点数。

定理2 对于给定的一组作业，Hadoop集群的总能耗是由其运行总时间（总完工时间）决定的。

证明 设置α＝Pmin，β＝Pmax－Pmin，T＝∑Ti，L是Hadoop集群的总负载，由公式（10）我们可以得到：

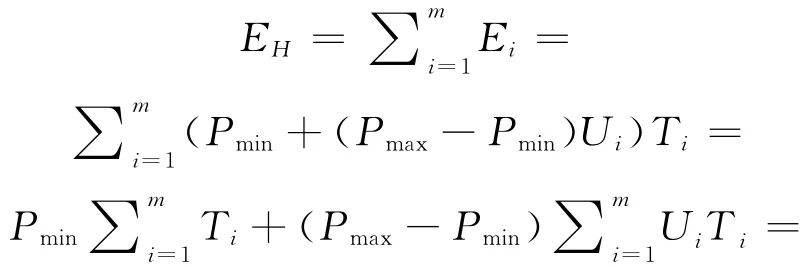
对于给定的一组任务，集群的总工作负载L是固定的，α和β都是常数，那么集群的总能耗是由其总完工时间（总运行时间）确定的。 □

定理2告诉我们，在设计多MapReduce任务时，为了降低能耗，应尽可能降低所有任务的总完工时间，这正是本文提出分析模型的一个应用出发点。

5 资源池负载均衡问题的优化解决方案

在文献［6，12］中，作者提出了一个叫做BalancedPools的启发算法。这个算法迭代地将任务分配到两个池中，然后尝试对每一个池进行适当的资源分配，以保证这些池的Makespan是均衡的。在每一个池中应用Johnson算法进行作业调度，此时Map和Reduce阶段的持续时间被估算出来。一个池中的Makespan是通过模拟器SimMR［5］进行预估的，BalancedPools算法的时间复杂度为Ο（n2lognlogm），其中，n是任务总数，m是在Hadoop中的节点数［6，12］。文献［6］指出了在系统可分配slots资源大于作业请求的slots资源进行作业共享资源时，该问题是NP－hard问题（关于NPhard问题参考文献［16］）。

定理3 使用引理1，对于两个池中的MapReduce作业集，平衡系统的MapReduce slots以实现两个池的Makespan平衡的问题不是NPhard，而是可在线性时间内解决的。

证明 这是因为按照引理1，分配MapReduce slots可以基于系统中可用的MapReduce slots进行动态调整。假设在给定的Hadoop集群中有P×P个MapReduce slots，所有请求（作业）可以根据池A和池B进行分组，每一个请求MapReduce slots（RA，RB），持续时间为（TA，TB）。注意到TA和TB可以通过Johnson算法很轻易地计算出来。假设整个Hadoop集群分为P1和P2slots两个池，以达到负载均衡。在理想负载均衡条件下，对于池A和池B中平衡后的Makespan（完工时间），我们可建立以下关系：

结合式（12）和式（13），我们可以解出P1和P2：

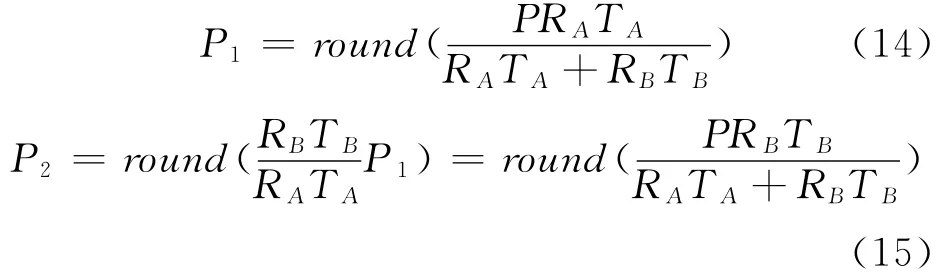
其中round（）是就近取整函数，根据定义round（X）可以取得离X最近的整数。这是两组作业分配给两个池的最优化结果。注意到分配资源的数量（P1，P2）是基于负载均衡的，所以结果可能与它们请求的MapReduce slots数量不同。□

例4 假设有两组请求，使用与例2相同的示例，我们知道R1＝30，R2＝20，P＝30。对于每一个池（组），我们通过使用公式（5）计算出其总的完工时间，分别为T1＝14，T2＝40。通过式（12）和式（13），可以得到P1＝10，P2＝20，池1和池2的Makespan分别是39和40个单位时间。这与文献［2］中得到的结果相一致。我们在下面提供另外一个示例。

例5 我们在两个池中随机生成4个任务，

A：J1＝（mi，ri）＝（3 ，5），J2＝（7 ，11），R1＝R2＝10×10个MapReduce slots；

B：J3＝（13 ，17），J4＝（23 ，29），R3＝R4＝20×20个MapReduce slots；P＝30。通过对每个池使用Johnson算法，我们可以计算出T1＝21和T2＝65。通过式（12）和式（13），我们可以得到P1＝4，P2＝26，池A和池B的Makespan在平衡过后分别为53和50个单位时间。如果我们应用引理1，对所有的作业增加MapReduce slot到30×30个slots（这也是所有可用的slots的总数）。这样它们的Map和Reduce持续时间将为J′1＝（1，5／3），J′2＝（7／3，11／3），J′3＝（26／3，34／3），J′4＝（46／3，58／3）。现在我们再应用Johnson算法，将得到所有的Makespan为，这个结果比用两个池所得出的结果（53）小。

例6 让我们使用文献［6］中的示例。考虑两个相同的作业J1和J2，J1＝J2＝（10，10），他们在Hadoop集群中请求30×30个Map和Reduce slots。假设两个作业都可使用集群上最大可用的30×30个Map和Reduce slots。

（1）使用两个池：通过对池1和池2进行负载均衡，应用式（12）和式（13），我们可以得到T1＝T2＝10，P1＝P2＝15；每一个池的Makespan是40个单位时间，这和文献［6］中使用HFS调度器得到的结果相一致。

（2）在单个集群上使用引理1和Johnson算法，J1先执行，J2紧接其后，我们可以轻松计算出总Makespan为30个单位时间。这和文献［2］中应用FIFO调度器得出的结果相一致。这个例子再一次说明，通过Johnson算法和引理1得出的总的Makespan比文献［6］中使用两个池方法得出的结果小。通过大量的例子和研究，我们得出下面的观察结果。

观察结果4 使用资源池可以使两组池的完工时间更加平衡，但未必会让所有作业的总完工时间最少，使用引理1和Johnson算法在单个Hadoop集群中总能保证总完工时间最小。

引理1、定理1、定理2、定理3和观察结果4告诉我们：

（1）在满足Johnson算法的条件下，我们仍然可以对单Hadoop集群使用Johnson算法来获取总完工时间的最小值；

（2）针对两个池完工时间的平衡，可以在线性时间内解决，远低于文献［6］中模拟方法的复杂度（其计算复杂度为O（n2lognlogm），其中n为任务数，m为Hadoop集群节点数）。

6 结束语

本文通过分析经典Johnson算法与MapReduce模型两个阶段的特征，改进MapReduce调度系统设计使其与经典Johnson应用条件相互匹配，因Hadoop为开源软件，这使得引理1容易实现，从而使用该算法来准确求解一批任务的最小总完工时间。为此，我们提出一个更好的调度策略，依据系统总的可用资源动态调整分配给不同任务的资源，以便最大化利用系统资源和满足用户请求。该模型可以非常方便地应用于提高系统总的响应效率、降低总体能耗、实现多个资源池的负载均衡等领域。

针对提出的模型，我们正在进行一些拓展研究：

（1）在真实Hadoop集群环境下，使用真实或模拟产生的数据进行大量分析测试，以修正理论模型与实践经验之间可能存在的差异；

（2）分析不同种类MapReduce任务的特征，对Hadoop集群多任务调度进行更好的管理，提高服务质量并兼顾节能以及负载均衡等策略；

（3）本文主要考虑Hadoop集群节点同构的情况，当集群节点不同构时，如何修正完善分析模型是另一个拓展方向。

［1］ http：／／hadoop.apache.org／common／docs／ro.20.1／capacityscheduler.htm.

［2］ Zaharia M，Borthakur D，Sarma J S，et al.Delay scheduling：A simple technique for achieving locality and fairness in cluster scheduling［C］∥Proc of EuroSys，2010：265－278.

［3］ Wolf J，Rajan D，Hildrum K，et al.FLEX：A slot allocation scheduling optimizer for MapReduce workloads［C］∥Proc of ACM／IFIP／USENIX International Middleware Conference，2010：1－20.

［4］ Verma A，Cherkasova L，Campbell R H.ARIA：Automatic resource inference and allocation for MapReduce environments［C］∥Proc of ICAC’11，2011：235－244.

［5］ Verma A，Cherkasova L，Campbell R H.Play it again，Sim－MR！［C］∥Proc of Intl.IEEE Cluster’11，2011：253－261.

［6］ Verma A，Cherkasova L，Campbell R H.Orchestrating an ensemble of MapReduce jobs for minimizing their makespan［J］.IEEE Transactions on Dependable and Secure Computing，2013，10（5）：314－327.

［7］ Tian Wen－hong，Yeo C S，Xue Rui－ni，et al.Power－aware scheduling of real－time virtual machines in cloud data centers considering fixed processing intervals［C］∥Proc of IEEE CCIS’12，2012：337－341.

［8］ Tian Wen－hong，Xue Rui－ni，Xiong Qing，et al.An energyefficient online parallel scheduling algorithm for cloud data centers［C］∥Proc of IEEE Services 2013，2013：1.

［9］ Tian Wen－hong，Zhao Yong，Zhong Yuan－liang，et al.Dynamic and integrated load－balancing scheduling algorithms for cloud data centers［J］.Journal of China Communications，2011，8（6）：117－126.

［10］ Herodotou H，Babu S.Profiling，what－if analysis，and cost based optimization of MapReduce programs［J］.Proc of the VLDB Endowment，2011，4（11）：1111－1122.

［11］ Moseley B，Dasgupta A，Kumar R，et al.On scheduling in Map－Reduce and flow－shops［C］∥Proc of SPAA’11，2011：289－298.

［12］ Verma A，Cherkasova L，Campbell R H.Two sides of a coin：Optimizing the schedule of MapReduce jobs to minimize their makespan and improve cluster performance［C］∥Proc of MASCOTS’12，2012：11－18.

［13］ Johnson S.Optimal two－and three－stage production schedules with setup times included［J］.Naval Research Logistics Quarterly，1954，1（1）：61－68.

［14］ Beloglazov A，Abawajy J，Buyya R.Energy－aware resource allocation heuristics for efficient management of data centers for cloud computing［J］.Future Generation Computer Systems，2012，28（5）：755－768.

［15］ Chen Y，Keys L，Katz R H.Towards energy efficient MapReduce［R］∥Technical Report No.UCB／EECS－2009－109，Berkeley：University of California，2009.

［16］ Garey M，Johnson D.Computers and intractability：A guide to the theory of NP－completeness［M］.USA：WH Freeman＆Co，1979.