基于多样性特征的JPEG图像隐写分析

李明则，向 阳，张文华，梁 礼

(西安通信学院 a.研究生管理大队；b.信息服务教研室；c.基础部，西安 710106)

1 概述

隐写分析是隐写的逆过程，它主要利用信息嵌入会改变载体数据统计特性这一事实，来检测提取或破坏隐藏在载体数据中的秘密信息。根据适应范围，隐写分析可分为2类：专用隐写分析[1]与通用隐写分析[2-4]。前者针对特定的隐写算法进行检测，效果较好但适应性不高；后者能分析多类隐写算法，但对具体的隐写算法，检测效果较差。在现实应用中，由于无法得知被测文件所用的隐写方法，因此通用隐写分析开始占据主流。现今的通用隐写分析方法大都是针对小范围隐写算法来研究，如：文献[2]提出在DCT域结合Markov链与直方图特征，能较好地检测JPEG域直接嵌入隐写；文献[3]根据DCT系数之间的依赖性，提取共生矩阵特征，对变换域隐写算法的检测效果较好；文献[4]根据空域相邻像素的相关性提取共生矩阵特征，它对空域隐写算法检测效果较好，但是至今没有一种通用的特征能综合有效地分析各种类型的隐写算法。

尽管现代隐写利用各种技术减小嵌入失真，但仍会不可避免地改变载体的统计特性。不同的隐写算法会对载体的不同统计特性产生影响，所以从单域空间提取的特征难以捕捉到不同隐写所带来的统计变化。本文从不同域提取21个特征子集，合计6424维特征，构成一个多样性特征组合模型。它由3个部分组成：(1)DCT域特征：系数直方图特征函数、块内块间系数残差的共生矩阵特征以及块内块间联合系数密度统计特征；(2)空域特征：相邻像素残差共生矩阵特征与相邻像素残差直方图统计特征；(3)小波域特征：三级小波系数低频直方图特征函数与一级小波系数残差共生矩阵特征。为了验证模型的有效性，选用了 4种典型的JPEG隐写算法：nsF5，PQE，MB，BCHopt，在小嵌入率下测试。针对特征维数大训练耗时长的问题，本文通过前向选择与穷举结合的方法，从多样性特征组合模型中选取最优的4个特征子集，将其维数降到1500以内，以优化检测效果。

2 多样性特征组合模型

自然数字图像的相邻系数(像素)之间存在一定相关性，隐写嵌入后这种相关性会遭到破坏[5]。由于图像之间本身差异远超过了含密图像与其载体之间的差异，因此直接用图像相邻系数(像素)的共生矩阵很难体现隐写带来的影响，相邻系数(像素)之差(残差)则能很好地消除图像内容的影响，残差共生矩阵能更好地区分载体和含密图像。

本文构建的多样性特征组合(Diversity Features Combination, DFC)模型，主要从不同域提取相邻系数(像素)各阶残差的各阶共生矩阵辅以直方图作为特征。DFC模型包含21个特征子集，共6424维特征。

2.1 基本定义与公式

所有共生矩阵中提到的阈值都满足：

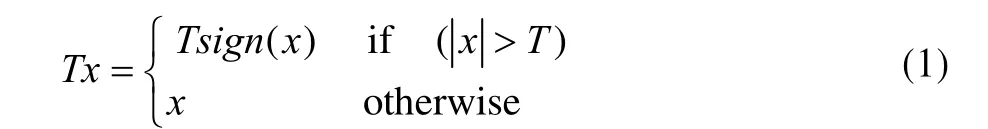
特征名的表示方式：domain_type_other表示在domain域用type方法的特征(如domain_aDbD表示domain域a阶残差b阶共生矩阵)。domain：JPEG域块内为dctIntra，块间为dctInter；空域为spatial，小波域为wavelet。HCF表示直方图特征函数，hist表示直方图统计特征。other表示其他。对于共生矩阵的阈值，1阶阈值为5，2阶阈值为4，3阶阈值为3，4阶阈值为2。

2.2 DCT域特征

DCT域具有以下特征：

(1)dctIntra_1D1D：从DCT域块内的水平、垂直、对角、反对角 4个方位求联合密度共生矩阵，再结合微观校准方式得到特征，然后结合校准前后之间的差值、商值得到216维特征。

(2)dctIntra_HCF：通过文献[3]中提到的DCT相邻系数之间的关系，提取直方图特征函数193维。

(3)dctIntra_HCF_New：结合微观校准与文献[2]的直方图特征函数提取方式，得到新校准的193维特征。

(4)dctIntra_HCF_diff：dctIntra_HCF_New 与 dctIntra_HCF的差值。

(5)dctIntra_HCF_div：dctIntra_HCF_New 与 dctIntra_HCF的商值。

(6)dctIntra_aDbD(dctInter_aDbD)：对块内(块间)DCT 域系数从水平、垂直、对角、反对角 4个方位取其残差的共生矩阵的平均值。

(7)dctIntra_aDbD_Car(dctInter_aDbD_Car)：上面特征的笛卡尔积校准[6]。其中，a取1和3；b取3。

2.3 空域特征

空域具有以下特征：

(1)spatial_aDbD(spatial_aDbD_ix)：从水平、垂直、对角、反对角 4个方位对其相邻像素的残差求共生矩阵，然后取其平均值，ix表示以上4个方向的反向特征。其中，a取3；b取3和4。

(2)spatial_hist_2D(spatial_hist_3D)：分别求图像相邻像素取 2(3)阶残差，然后对残差后的系数取直方图统计特征各256维。

2.4 小波域特征

小波域具有以下特征：

(1)wavelet_HCF：图像经小波三级分解后得到13个小波子带，然后对这些子带的系数直方图进行傅里叶变换，最后计算变换之后子带的3阶特征函数，得到39维特征，然后参考 xuan[7]的校准，提取相同特征，最后得到一个78维的直方图特征函数。

(2)wavelet_2D2D：取图像一级小波分解的低频子带，提取其水平、垂直、对角、反对角，4个方位的块内块间2阶残差2阶共生矩阵，取其平均值各81维，合成162维特征。

综上所述，DFC模型包含特征子集为：DCT域13个，空域6个，小波域2个，共21个特征子集，总共6424维。

3 DFC模型性能分析

为了分析该组合模型性能，实验用了 4种典型隐写算法，分类器选用了对高低维特征都有速度快且分类效果稳定的 ensemble分类器[8]。它是从特征集中选取不同的特征子空间，利用 Fisher线性分类器分类来构建多个最优学习机(用最低错误率决定其特征子空间的维数)，最后由这些学习机投票决定分类结果。

3.1 实验环境

实验选用了 4种隐写算法，分别是nsF5、MB、PQ、BCHopt。

nsF5[9]是在传统 F5[10]的基础上的加入了综合编码的优化算法，MB[11]是由Sallee提出的基于整体模型匹配的隐写算法，两者都属于在JPEG域直接隐写的算法。

PQ[12]是选取量化过程中失真较小的系数进行嵌入，达到减小扰动量，并结合湿纸编码[13](wet paper codes)来达到量化失真最小原则。本文选用的PQ算法是在PQ操作的基础上加入了权值操作 energy的 PQE算法，它的抗检测性更强。

BCHopt[14]是在 DCT域对没有取整的 DCT系数使用BCH纠错编码方法来最小化嵌入失真，然后加入启发式优化来隐藏信息，它属于边信息嵌入编码。

实验所用图像库是 ucid[15]经灰度处理后的图像库，图像尺寸为512×384(384×512)，共1337张。实验生成图像库是从图像库中随机抽取1000张图像当成训练载体，剩余图像为测试图像，这里采用统一的质量因子75。

3.2 性能评估指标

对于每种隐写算法都使用了不同的嵌入率，即在每位非零 AC系数中的嵌入改变率，然后分别对它们构建分类器，最后进行测试，测试的标准如式(2)所示：

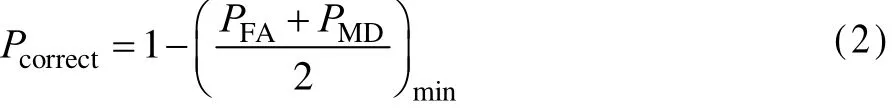
参与比较的特征有：

Liu[3]：利用块内块间相邻系数密度的依赖性关系求联合密度矩阵216维特征。

ccchen[16]：利用卷积的方法求块内块间共生矩阵特征，并结合笛卡尔积校准组合而成的972维特征。

ccpev[2]：融合DCT域块内之间的依赖性得到193维直方图特征与一阶共生矩阵81维特征，再结合笛卡尔积校准组成的548维特征。

CDF1234：从空域8个方位提取三阶共生矩阵686维特征，即spam[4]，再与DCT域特征ccpev组合成1234维特征。

ccJRM[17]：利用块内块间DCT系数之间的统计依赖性关系，从DCT域各个方位提取系数绝对值、系数残差共生矩阵特征，组合成22510维特征。

3.3 实验结果与分析

为了能够更好地分析DFC模型对于各类隐写算法的检测率，实验选用多种高低维特征与之比较，结果如表 1所示。

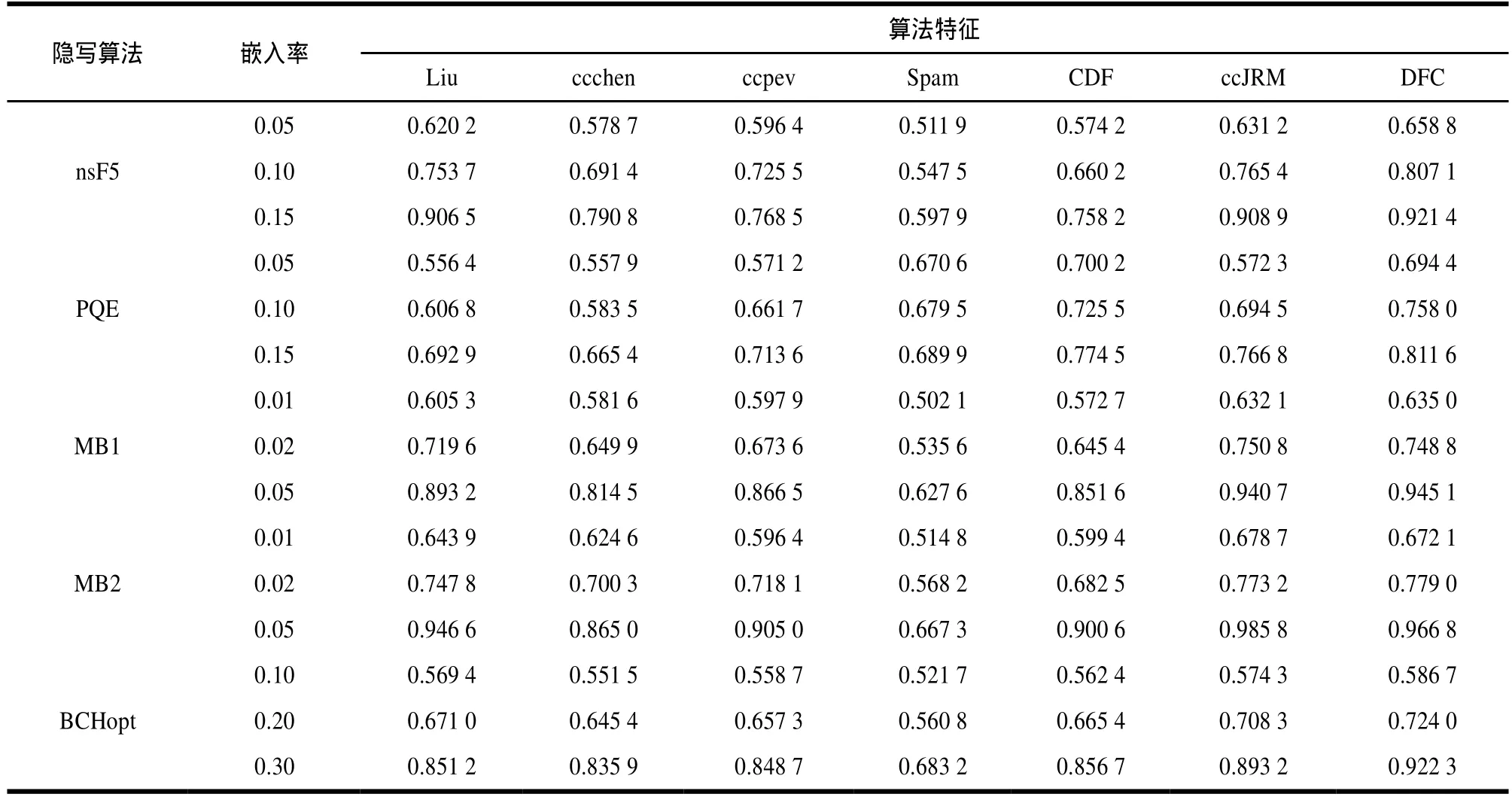
表1 不同特征对于小嵌入率隐写算法的检测效果

从表1可以看出，DFC模型对于各种嵌入率下的隐写算法检测效果都比较好，从实验也可以得出以下结论：

融合了ccpev与spam的特征CDF在分析检测PQE与BCHopt算法时，有一定的优势，尤其是对于PQE算法的检测优势明显，但是对于MB与nsF5算法，它的检测准确率反而比ccpev要低，从中可以看出，简单的跨域特征结合并不意味着分析检测效果就能提高。

对于不同的隐写算法，都有对它检测效果较好的特征。如：Liu对MB检测效果较好，CDF对PQE检测效果较好，ccJRM能较好地检测nsF5、MB、BCHopt，但是对于PQE，它的检测效果并不理想。基于多样性特征融合的DFC模型能很好检测以上所有算法，并且与ccJRM的22510维特征相比，它的维数要低得多。

3.4 DFC模型特征选择

尽管DFC模型在隐写分析中具备一定优势，但它的维数太大，影响了隐写分析的性能。为了降低特征维数，实验通过选择最优特征子集组合进行降维操作。

3.4.1 前向选择法

实验选用DCF模型21个特征子集中检测效果最好的前8个，通过前向选择方法得到的检测结果如图1所示，其中，图1(a)中[1～8]分别表示的是dctIntra_1D1D，dctInter_3D3D_Car，dctIntra_3D3D_Car，dctIntra_HCF，dctIntra_HCF_diff，dctIntra_3D3D，dctIntra_HCF_div，spatial_3D3D；图1(b)中[1～8]分别表示的是：spatial_3D4D，wavelet_HCF，spatial_3D3D，spatial_3D4D_ix，dctIntra_2D2D，wavelet_2D2D，dctInter_3D3D_Car，spatial_3D3D_ix；图 1(c)中[1～8]分别表示的是：dctIntra_1D1D，dctIntra_HCF，dctInter_3D3D_Car，dctIntra_HCF_diff，dctIntra_3D3D_Car，dctIntra_1D3D_Car，dctIntra_HCF_New，spatial_3D3D_ix；图 1(d)中[1～8]分别表示的是：dctIntra_1D1D，dctIntra_ 3D3D_ Car，dctInter_3D3D_Car，dctIntra_HCF，dctIntra_ HCF_diff，dctIntra_1D3D_Car，dctIntra_HCF_New，spatial_ hist_3D。

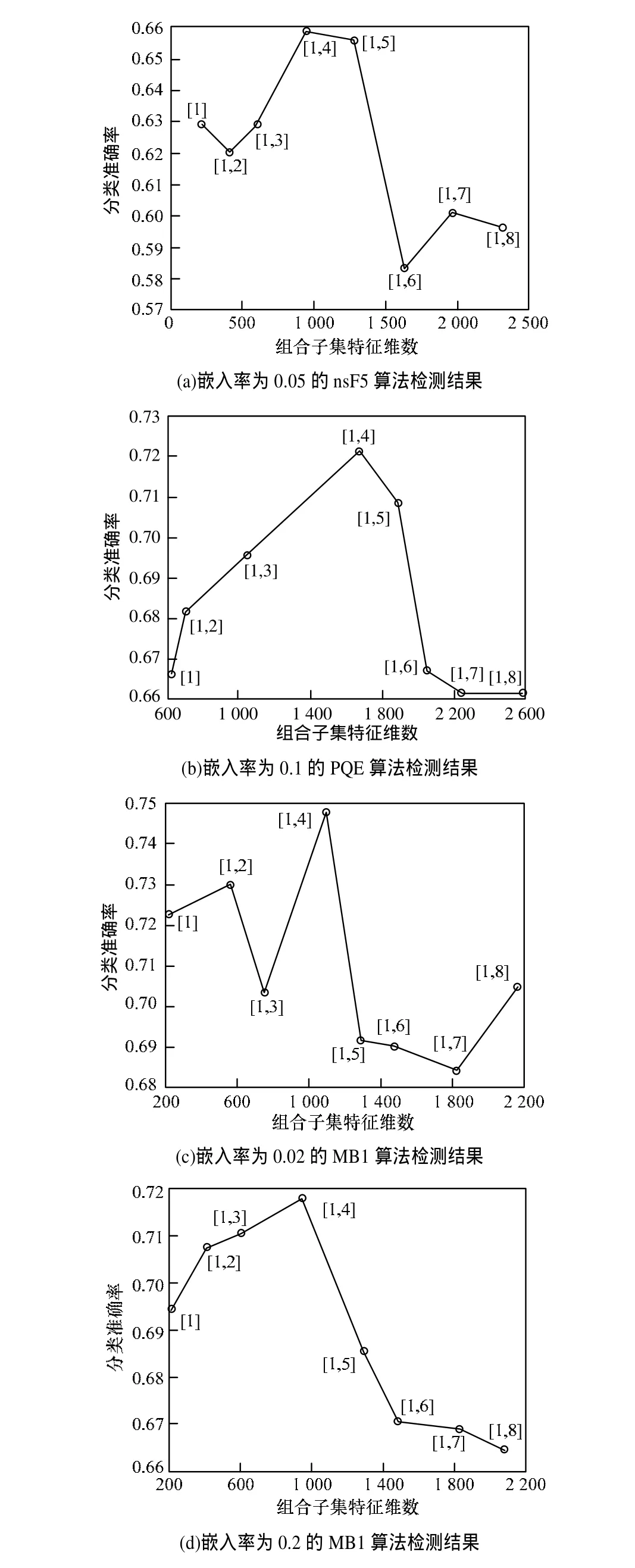
图1 前向选择特征对各隐写算法的检测结果

实验结果表明，前向选择法得不到稳定结果，当子集数低于4时，前向选择检测准确率呈上升趋势，超过4后，则无规律可循。说明特征子集数量与检测结果不是等价的正比关系，它不仅跟隐写算法有关，还与选用的特征有关。从中可得到一个结论：并不是把检测效果好的特征进行组合就一定能起到促进作用，有时会起到反效果，如在图1(a)～图1(d)中，当子集超过4个后，检测效果都有所下降。

3.4.2 最优四元组

穷举法能获取各隐写算法的最优特征子集组合，但它的复杂度太大。根据上面实验，当子集数为 4时，分类结果最接近最优解。所以，本文先从21个子集中选择最优的12个子集，然后通过穷举法，从12个子集中选择效果最好的4子集组合，生成最优四元组子集，最后把它与整个DFC模型做比较。检测结果如图2所示。

图2 各隐写算法的检测结果

在图 2(a)中，1～12分别表示的是：dctIntra_1D1D，dctInter_3D3D_Car，dctIntra_3D3D_Car，dctIntra_HCF，dctIntra_HCF_diff，dctIntra_3D3D，dctIntra_HCF_div，spatial_3D3D，dctIntra_1D3D_Car wavelet_HCF，dctInter_1D3D，spatial_hist_3D；在图2(b)中，1～12分别表示的是：spatial_3D4D，wavelet_HCF，spatial_3D3D，spatial_3D4D_ix，dctIntra_2D2D，wavelet_2D2D，dctInter_3D3D_Car，spatial_3D3D_ix，dctIntra_3D3D_Car，dctIntra_HCF_diff，dctIntra_HCF，spatial_hist_3D；在图 2(c)中，1～12分别表示的是：dctIntra_1D1D，dctIntra_HCF， dctInter_3D3D_Car，dctIntra_HCF_diff，dctIntra_3D3D_Car，dctIntra_1D3D_Car，dctIntra_HCF_New，spatial_3D3D_ix，spatial__3D4D，wavelet_HCF，spatial_3D3D，spatial_3D4D_ix；在图 2(d)中，1～12 分别表示的是：dctIntra_1D1D，dctIntra_3D3D_Car，dctInter_3D3D_Car， dctIntra_HCF，dctIntra_HCF_diff，dctIntra_1D3D_Car，dctIntra_HCF_New，spatial_hist_3D，spatial_3D4D_ix，spatial_3D3D_ix，spatial_3D3D，wavelet_HCF。图中13表示最优四元组，all表示DFC模型。图2(a)中 13由 1、4、9、11组成；图 2(b)中 13由 1、3、9、10组成；图2(c)中13由1、3、4、8组成；图2(d)中13由2、5、10、11组成。

(1)单个子集比较

对于不同的隐写算法，单个子集检测结果差异较大。如图2(b)中第2个子集spatial_3D3D检测PQE效果较好，但检测BCHopt时，准确率排第11，这说明各个子集对不同的算法有着不同的贡献。

对于同残差的不同共生矩阵，高阶共生矩阵比低阶共生矩阵的检测效果要好。但是对于同共生矩阵的不同残差，高阶残差并不一定比低阶残要好。如图2(b)中DCT域块间的3阶共生矩阵，3阶残差dctInter_3D3D_Car比1阶残差dctInter_1D3D_Car要好，而在图2(a)中，DCT域块间1阶残差dctInter_1D3D比3阶残差dctInter_3D3D要好。

经笛卡尔积校准的特征子集检测性能，比没经过笛卡尔积校准的特征子集检测性能要好，而差值校准、商值校准刚好相反。

(2)子集组合比较

最优四元组并不是前向选择组合，它与前向选择相比正确检测率要更高。如：对于PQE的检测，图1(b)前向选择检测准确率最高为 0.72，而图 2(b)中最优四元组检测正确率超过了 0.75。从图2也可以看出，尽管有些单个子集检测率很低，如：图2(d)中第11个子集spatial_3D3D，它单独检测时比最优单个子集要低 10%以上，但是它们参与的最优组合，要比单独检测表现最好的 4个子集的组合检测率更高。

所以，最优的特征组合并不是简单地对检测性能好的特征进行拼凑，要尽量选择互补的特征，这样才能充分检测出隐写带来的统计特性变化。最优四元组跟整个特征模型相比，它的维数能降到1500以下，但是检测性能不但没有降低，有的甚至略有提高。这也说明，该种降维方法是行之有效的。

4 结束语

本文根据各域空间系数(像素)之间存在的依赖性关系，从各域空间中提取不同特征构建多样性特征组合模型，该模型对于小嵌入率的不同隐写，检测效果好于已有算法。通过前向选择与最优四元组2种选择方法，对DFC特征集进行降维。实验结果表明，由各个检测性能差异大的特征子集组成的最优四元组特征，检测效果明显优于前向选择方法构造的由 4个独立检测效果最优的特征子集组合而成的特征集，这说明单独检测效果好的特征的叠加并不是提高分类效果的最好方法，特征选择考虑从多样性特征的组合着手，利用互补原则提高隐写分析检测性能。对于最优特征组合，尽管检测效果得到提高，但组合择优选择时间太长，下一步将针对多样性特征组合选择更好的降维方法。

[1]张 涛, 平西建, 徐长勇.基于图像平滑度的空域 LSB 嵌入的检测算法[J].计算机辅助设计与图形学学报, 2006,18(10): 1607-1612.

[2]Pevny T, Fridrich J.Merging Markov and DCT Features for Multi-class JPEG Steganalysis[C]//Proceedings of SPIE’07.San Jose, USA: [s.n.], 2007: 1-34.

[3]Liu Qing.Steganalysis of DCT-embedding Based Adaptive Steganography and YASS[C]//Proceedings of ACM Multimedia & Security Workshop.[S.1.]: ACM Press, 2011: 77-86.

[4]Pevný T, Bas P, Fridrich J.Steganalysis by Subtractive Pixel Adjacency Matrix[J].IEEE Transactions on Information Forensics and Security, 2010, 5(2): 215- 224.

[5]黄方军, 黄继武.基于图像校准的通用型JPEG隐写分析[J].中国科学F辑: 信息科学, 2009, 39(4): 383-390.

[6]Kodovsky J, Fridrich J.Calibration Revisited[C]//Proceedings of the 11th ACM Multimedia & Security Workshop.[S.1.]:ACM Press, 2009: 63-74.

[7]Shi Yunqing, Xuan Guorong, Yang Chengyun, et al.Effective Seganalysis Based on Statistical Moments of Wavelet Characteristic Function[C]//Proceedings of IEEE International Conference on Information Technology.[S.1.]: IEEE Press,2005, 768-773.

[8]Kodovský J, Fridrich J.Steganalysis in High Dimensions:Fusing Classifiers Built on Random Subspaces[C]//Proceedings of SPIE Electronic Imaging, Watermarking,Security and Forensics of Multimedia XIII.San Francisco,USA: [s.n.], 2011: 1-13.

[9]Kodovsk J, Fridrich J, Pevny T.Statistically Undetectable JPEG Steganography: Dead Ends, Challenges and Opportunities[C]//Proceedings of the 9th ACM Multimedia & Security Workshop.[S.1.]: ACM Press, 2007: 20-21.

[10]Westfeld A.F5-A Steganographic Algorithm High Capacity Despite Better Steganalysis[C]//Proceedings of the 4th International Workshop on Information Hiding.[S.1.]: IEEE Press, 2001, 289-302.

[11]Sallee P.Model-based Steganography[C]//Proceedings of International Workshop on Digital Watermarking.Berlin,Germany: Springer-Verlag, 2004: 154-167.

[12]Fridrich J, Goljan M, Soukal D.Perturbed Quantization Steganography Using Wet Paper Codes[C]//Proceedings of the 6th ACM Multimedia & Security Workshop.[S.1.]: ACM Press, 2004: 4-15.

[13]Fridrich J, Goljan M, Soukal D, et al.Wet Paper Codes with Improved Embedding Efficiency[J].IEEE Transactions on Information Forensics and Security, 2006, 1(1): 102-110.

[14]Sachnev V, Kim H J.Less Detectable JPEG Steganography Method Based on Heuristic Optimization and BCH Syndrome Coding[C]//Proceedings of the 11th ACM Multimedia &Security Workshop.[S.1.]: ACM Press, 2009: 131-140.

[15]Schaefer G, Stich M.Uncompressed Colour Image Database v2.03[EB/OL].(2010-08-16).http://vision.cs.aston.ac.uk/ datasets/UCID/data/ucid.v2.tar.gz.

[16]Chen Chunhua, Shi Yunqing.JPEG Image Steganalysis Utilizing Both Intrablock and Interblock Correlations[C]//Proceedings of IEEE International Symposium on Circuits and Systems.Seattle, USA: IEEE Press, 2008: 3029-3032.

[17]Fridrich J, Kodovský J.Rich Models for Steganalysis of Digital Images[D].New York, USA: Department of Electrical and Computer Engineering, Binghamton University, 2012.