一种适用于CORS省级大地水准面模型简易建立方法

葛 奎，张从宝，方国锋

(安徽省电力设计院，安徽 合肥 230601)

随着国内全球卫星定位技术在各个行业的广泛应用及各行各业对测绘数据的需求，很多政府部门(特别是测绘部门)、行业都陆续建立自己的全球运行连续参考站系统(CORS)，供全社会或者本行业应用。CORS建成后，所直接获取点坐标为WGS84坐标，对应的高为椭球高，而我国使用的高程是基于似大地水准面的正常高，需使用高程拟合或大地水准面模型的方法进行改正。高程拟合方法一般只用于小区域，CORS系统的覆盖范围一般较大，需使用大地水准面模型进行改正，在大区域内一般需要通过使用区域似大地水准面精化的方法进行，用GPS技术结合区域内的地面重力资料、水准资料、高分辨率的地形数据以及最新的重力场模型，精确研究并确定区域似大地水准面，以求取高精度的高程异常，目前各个省份测绘局所建立的CORS系统中，进行水准面精化基本均使用此方法，其采用多种且大量的数据，具有区域大、精度高的特点，但由于此方法所使用的多种重力数据为保密资料，且进行水准线路测量耗时耗力，GPS测量点位密度大且需要长时间的观测，总体费用过大、时间较长，导致一般单位无法利用此方法建立属于自己工程使用的大地水准面模型。为了快速、简易的建立适用于本行业的大地水准面模型，本文在充分研究已有技术和以往水准面精化方法的基础上，提出了一种适用于CORS省级大地水准面模型简易建立方法，并应用于实践。

1 基本原理

2008年4月，美国NGA充分利用各种数据历时4年研发的新一代高阶地球重力场模型-EGM2008，阶次达到2 190 阶，将计算全球高程异常的精度提高了3～5 倍，在我国范围内的精度达到20cm(标准差)，华东地区为12cm，充分利用EGM2008高精度的重力场模型(WGS84)，结合已有的GPS/水准数据，选择合适的拟合函数对残差场进行拟合，建立高精度的大地水准面模型变为可能。大地高与水准高程存在关系见图1。

图1 大地高与水准高程存在关系

式中：H为大地高，Hr为正常高(或高程)，似大地水准面到椭球面的距离，称为高程异常，记为ξ。

构建大地水准面模型关键为准确计算测量点高程异常，由于我国采用的是1985国家高程系统(或1956黄海高程系)，与EGM2008采用的全球大地水准面基准有一定的差距，存在系统偏差。因此，利用EGM2008计算出的任一点的高程异常与GPS/水准高程异常存在如下关系：

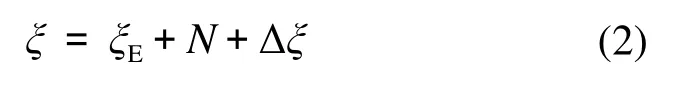
式中：ξE为EGM2008计算得到高程异常值；N为85高程基准和EGM2008所使用的全球高程基准的系统差；Δξ为GPS水准高程异常差值和EGM2008计算得到高程异常差值再除去系统差后的残差。

通过GPS水准获得一定数量准确的高程异常值，结合EGM2008重力场模型计算的高程异常，先计算出高程基准系统差N，再根据上式(2)计算所有已知点的高程异常残差值Δξ，然后通过对残差场进行拟合，计算任意点的高程残差值Δξ，最后再利用(2)式计算所有格网点的高程异常值ξ，从而构建最终的大地水准面模型。

2 高程基准系统差的计算

从理论上讲，1985国家高程系统的高程基准和全球似大地水准面模型的基准差应是一个常数，但实际上由于任一点测量点的垂直偏差还受到GPS 测量误差、水准测量累积误差以及重力场模型误差的影响，因而在各地区的具体值会出现不一致性，为此, 需对局部似大地水准面与似大地水准面的垂直偏差进行多项式拟合,以便准确地求出局部高程基准系统差的变化规律, 求解出最适合局部地区的高程系统基准差一般采用重力位方法，其计算过程较复杂且已有文献发表，本文不再赘述，有兴趣的可参考文献[7]、[8]；

根据基准系统差N的形成原理，其大小也可由下式进行估计，公式如下：

通过对安徽地区均匀分布的33个点，利用上式的计算结果为32.5cm，与引文[7]、[8]通过重力位的方法计算结果32cm及35.2cm一致,说明取平均值的方法是可行的。

3 高程异常残差场的拟合

高程基准系统差计算后，通过系统差对EGM2008模型计算的高程异常进行改正，其所得的高程异常已经具有了较高的精度，为进一步精化似大地水准面模型，得到更高的精度，则需对局部高程异常残差进一步拟合计算，高程异常残差拟合类似于高程拟合，高程拟合一般有多项式法、克里金法、多面函数法、反距离加权插值法等，它们各有自身的适用区域，综合比较各种拟合方法的优缺点，并考虑高程异常残差的分布特点，反距离加权插值法最适合于大区域高程残差场的拟合。

其数学公式如下：

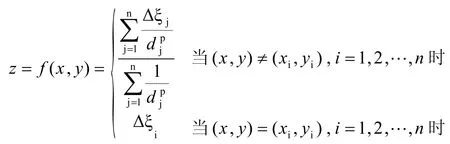
(xi, yi)为已知点平面坐标，高程异常残差为Δξi(也即Z)，i=1, 2, …, n。P为幂指数，其可控制插值函数曲面的形状。p越大，在节点处函数曲面越平坦；p越小，在节点处函数越尖锐。

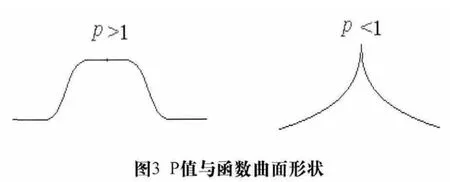
根据33个GPS/水准点在全省的分布情况，保持残差拟合的平滑性，选择幂指数为2的反权距离法用于高程残差场的拟合与计算。

4 省级大地水准面模型的建立

假如我们设计的大地水准面模型的格网点间隔为3.6′×3.6′，通过以上的步骤可知，利用EGM2008重力场模型计算的高程异常值格网点ξE，高程基准系统差N，通过反权距离拟合法计算格网点的高程异常残差Δξ。

利用公式 ξ = ξE+N+ Δξ即可计算所有格网点的高程异常。即为我们所要建立的省级大地水准面模型。见表1。

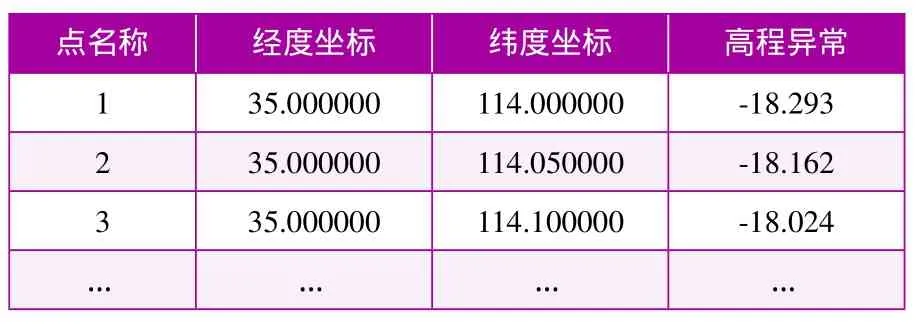
表1 高程异常网格

然后，利用此大地水准面模型，进行任意测量点大地高与高程之间的转换。

5 质量检验与校核

为了客观评定GPS水准计算的精度，在完成大地水准面模型建立后，应通过内业拟合残差和外业实地测量进行检核，以确定建立的大地水准面模型大地高转化为正常高的精度。由于本方法中内符合精度检查中，若无单独预留的高程异常(未参加残差拟合计算)，则无法使用内符合精度的检验方法。需通过外符合精度进行检验。

设检验点的高程异常ξi和拟合高程异常ξi′,求出拟合残差Vi= ξi′- ξi，按上式计算外符合精度。在第一次集中测试36个点，后期工程应用过程中，又校核了22点，共58个点进行实测校核，其外业校核结果统计如下：

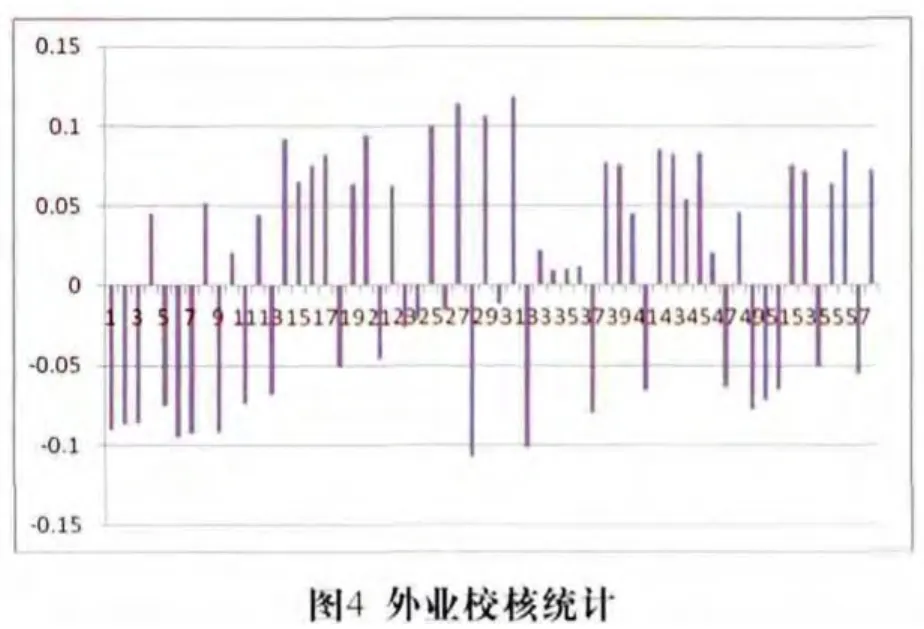
其中图4横坐标代表已知点的点数，纵坐标代表正常高和大地水准面模型计算高程校核差值，由图可知外业校核差最大12cm，最小1cm。

按外符合精度差值的绝对值的分类统计见表2。

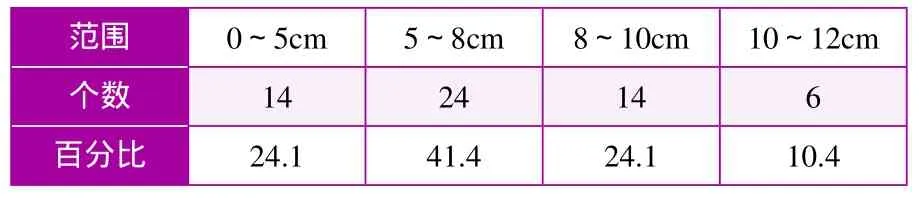
表2 外业校核误差分类统计

由统计结果可知，此方法建立的大地水准面模型精度分布均匀、可靠。

6 成果应用

500kV淝河—孔店输电线路工程，总长约70km，线路路径主要分布在平原和丘陵区域，沿线跨越河湖共五处，分别为淮河、涡河、茨河、茨维新河以及四方湖，且相互之间相距较远、河道较宽。为了满足设计及后续施工需要，沿主线路共布设了12个E级GPS控制点，并同期进行了四等水准测量，测得全部GPS控制点的高程。为了研究按上述方法建立的3.6′×3.6′大地水准面模型用于GPS 高程转换的精度，也联测了线路路径方向内6个GPS C级点，通过拟合的方法计算所有E级控制点的高程，并进行比较。结果见图5。

其中，蓝色表示大地水准面模型计算值与水准值比较结果，红线为利用GPS拟合计算值与水准值的比较，结果显示，大地水准面模型与GPS小区域拟合程度相当，能够满足一般工程精度要求。

7 结论

目前，大多数的勘测设计单位仍采用常规的小区域拟合转换和传统的几何水准方法进行水准联测，本文提出的适用于CORS省级大地水准面模型简易建立方法，通过简化的并考虑基准系统偏差的数学模型，使用EGM2008重力场格网模型和GPS/水准资料进行解算可得到优异的结果，简单、实用、高效。实践应用结果显示，所建立的大地水准面模型的精度，已能达到普通几何水准测量的精度要求，可以用于1∶1000及以下比例尺地形图测图和线路工程测量，以及其他一些对高程精度要求不是很高的行业和部门。

此方法也可应用于一般单位的水准面精化，从而取代传统的高程联测方法，显著提高外业效率。所建立的水准面模型区域大，应用范围广，可在相关行业进行推广。

[1]张全德.精化区域似大地水准面精化设计[J].测绘工程，2007，(04).

[2]郭东美，许厚泽.应用GPS水准与重力数据联合解算大地水准面[J].武汉大学学报(信息科学版)，2011，(05).

[3]张兴福，等.基于EGM2008重力场模型的GPS高程转换方法及精度分析[J].地球物理学进展，2012，(01).

[4]章传银，等.EGM2008地球重力场模型大中国大陆适用性分析[J].测绘学报，2009，(04).

[5]邓标，段德磊，洪绍明.区域似大地水准面精化中几个问题的探讨[J].水电自动化与大坝监测，2009，(05).

[6]朱亚光，等.基于EGM2008 重力场模型的高程联测方法[J].济南大学学报(自然科学版)，2011，(04).

[7]郭海荣，焦文海，杨元喜.1985国家高程基准与全球似大地水准面之间的系统差及其分布规律[ J].测绘学报2004，33( 2).

[8]翟振和，等.利用EGM2008位模型计算中国高程基准与大地水准面间的垂直偏差[J].大地测量与地球动力学2011，31(4).