基于模糊调节的两轮自平衡车的终端滑模分解控制

杨兴明， 段 举， 朱 建， 高银平

（合肥工业大学 计算机与信息学院，安徽 合肥 230009）

欠驱动系统是一类驱动器数目小于系统自由度数目的系统。两轮自平衡小车则是欠驱动系统的典型代表，它具有欠驱动、非线性、强耦合、多变量的特点。它可以在3个自由度上运动，包括摆杆的旋转，车体的前后运动以及车体的旋转。其广泛的应用前景引起了国内外学者的关注。由于非线性系统不能建立精确模型，传统PID、LQR等线性控制方法具有局限性，因而研究人员开始关注智能控制方法的应用，滑模控制、模糊控制、神经网络、迭代学习、遗传算法等控制方法的设计各有特点。其中，滑模控制的特点在于系统的“结构”并不固定，随着当前系统的状态不断变化，按照预定的“滑动模态”的状态作轨迹运动，因此滑模控制得到了广泛的应用［1］。其稳定性强，鲁棒性较好，实现相对容易。

为实现对小车的平衡控制，文献［2］将其平衡控制系统分解为2个子系统，通过一个中间变量将2个子系统联系起来，用1个控制量实现对小车的平衡控制。但这种传统的分解滑模控制的局限性在于无论如何控制，系统状态在滑动模态上无法在有限时间内收敛至平衡点，且动态响应速度较慢。文献［3］提出引入模糊推理来调节线性滑模面的斜率参数，一定程度上加快了动态响应速度，却仍然存在有限时间内无法收敛的问题。

20世纪80年代，有学者提出终端滑模控制策略，通过引入非线性滑模面，系统状态能在有限时间内到达平衡点［4］。其缺点在于降低了收敛速度，且存在奇异性问题。通过增加线性项，快速终端滑模控制可以进一步改善收敛速度，但始终未能解决奇异性问题［5］。文献［6］提出一种新型快速终端滑模控制法，它表明在选取适当的分数幂的情况下可以避免奇异性，且收敛速度较快。然而，对于阶数较高的系统，此类方法的终端滑模控制器设计复杂，计算机仿真耗时较长。

为解决欠驱动两轮自平衡车的平衡控制问题，本文将分解滑模控制与新型快速终端滑模控制相结合，解决了有限时间收敛的问题。鉴于常值滑模面系数影响收敛速度，采用模糊推理法进一步调节，加快了系统状态响应速度，表现出较好的鲁棒性。此外，对于高阶系统而言，本文的控制方法相对于普通终端滑模控制方法设计简单，易于实现。

1 两轮自平衡车的模型建立

两轮自平衡车模型示意图如图1所示。

图1 两轮自平衡车模型示意图

设R为左右车轮的半径；mR＝mRL＝mRR为车轮质量；mP为车体质量；XRL、XRR为左右车轮的位移为车体的行驶速度（即ωP）为摆杆与垂直方向的夹角角度和角速度；θRL、θRR为左右车轮绕Z轴的转角为车体绕Y轴的角度和角速度；D为两车轮的间距；L为车体质心到Z 轴的距离；JR＝JRL＝JRR，JPδ、JPθ分别为左右车轮的转动惯量、车体绕Y轴的转动惯量、车体绕通过质心且平行于Z轴的转动惯量。

采用基于能量的分析方法［7］，选取车轮所在平面为零势能面，得到小车系统的动能T和势能V的方程：

系统的输入功率和输出功率为：

其中，CL、CR分别为电机对左、右车轮的转矩。

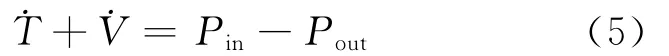
为了便于建模，将系统在平衡点附近进行线性化处理，即在小角度的范围内，取sinθP≈θP，cosθP≈1，忽略二次分量。基于上述方程，结合文献［7］中系统所受约束条件，可以得到系统模型的方程组：

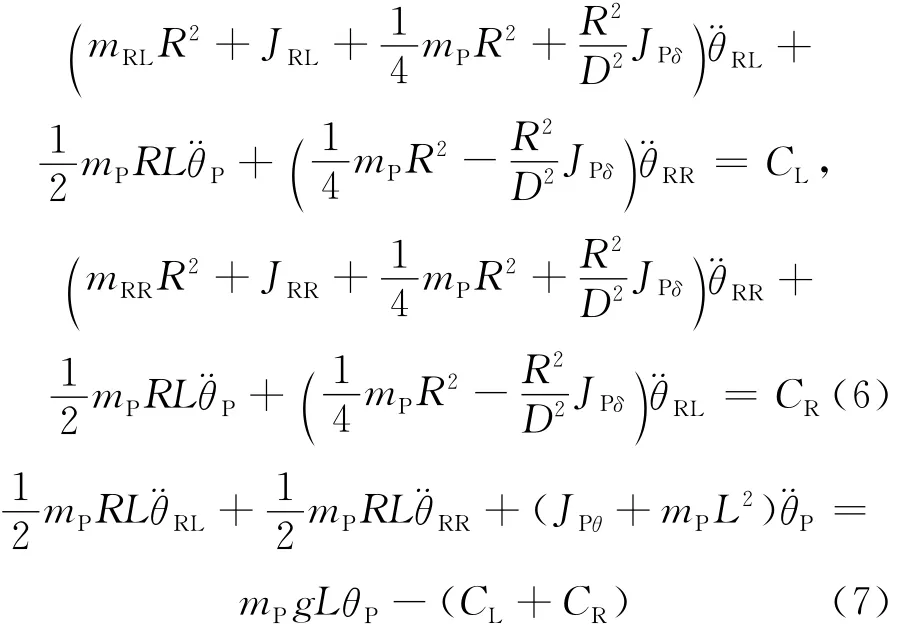
这里选取需要观察的状态变量为XRM、VRM、θP、

结合电机转矩C和控制电压U的关系：

其中，Km、Ke分别为电机力矩系数和电机反电动势系数。

整个系统的状态空间方程为：

其中

对系统解耦，并将（11）式代入，即

上述解耦得出的2个部分分别为小车的平衡控制部分与旋转控制部分，可看作是相互独立的，可分别对这2个部分进行控制。由于小车绕Y轴旋转的状态矩阵为定值，也不存在干扰，控制相对容易，故本文重点研究平衡控制部分［8］。

2 控制器设计

将（12）式简化为如下的系统：

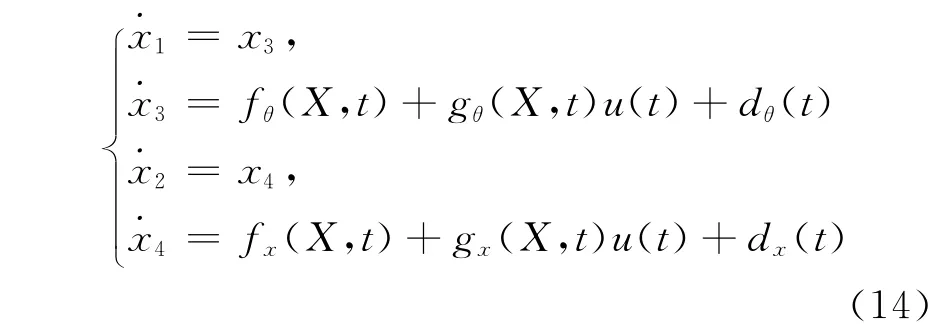
其中，x1＝θP，x2＝XRM，x3＝ωP，x4＝VRM；dθ（t）、dx（t）为外在的干扰，实际情况下它们都是具有上界的，即｜dθ（t）｜≤Dθ（t）、｜dx（t）｜≤Dx（t）；fθ（X，t）、fx（X，t）、gθ（X，t）、gx（X，t）的值可以由（12）式推出。

2.1 传统分解滑模控制器及其改进

将小车平衡控制部分分解为摆角子系统和位移子系统。摆角控制子系统记为子系统A，位移控制子系统记为子系统B。2个子系统的滑模面分别设计如下［2］：

其中，c1，c2＞0；z与s2是成比例的，可看作一个有界衰减振荡信号。定义：

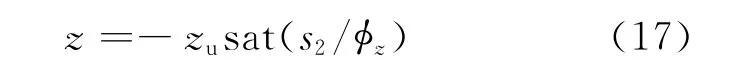
其中，0＜zu＜1；｜z｜≤zu；φz为s2的边界层厚度。显然z是s2的函数，当s2→0时，有z→0。

平衡控制的目标是控制摆角和位移渐进收敛为0。这里采用了分解控制的方法，引入能够反映子系统B滑模面信息的中间变量z，将其引入到子系统A的滑模面中，用1个控制量控制2个子系统，从而完成小车的平衡控制。此时，控制目标从普通滑模控制的x1＝0，x3＝0转变为x1＝z，x3＝0。

根据Lyapunov定理，令滑模面s1的导数为0，即

对方程进行求解，暂不考虑dθ，并将（14）式代入，得到等效控制律：

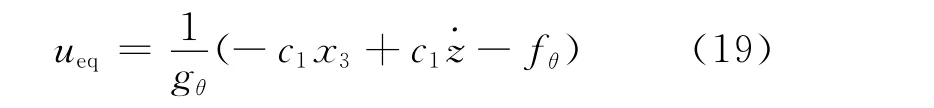
考虑到整个系统的稳定性，设计控制律为：

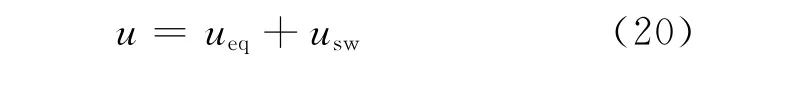
选取切换控制律：

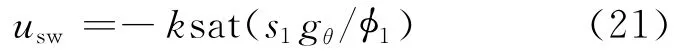
于是总的控制律为：

其中，k＞［Dθ（t）／｜gθ｜］；φ1为s1的边界层厚度，为正常数。饱和函数sat（·）用来抑制抖振现象，定义：

采用上述分解滑模控制器虽然能够较好地实现对小车平衡控制部分的解耦控制，但缺陷在于其收敛速度慢，且系统状态无法在有限时间内收敛。文献［3］使用模糊推理来调节滑模面系数，对其进行了改进。其滑模面设计如下：

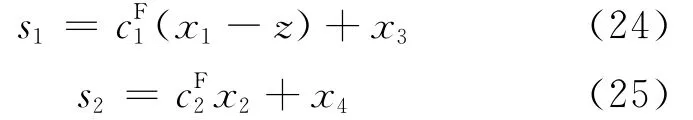
该方法针对传统方法滑模面系数为常值的缺陷，制定了一维模糊规则，将子系统的2个状态变量分别乘以比例系数，利用其差值进行模糊推理，得到可变的系数和，其余设计与传统方法类似，虽使得系统状态相对较快地趋近至平衡点附近，但由于其采用线性滑模面，始终无法实现滑动模态上的系统状态在有限时间内到达平衡点。

2.2 基于模糊调节的终端滑模分解控制器

针对上述分解滑模控制法的系统状态收敛速度较慢，不能在有限时间收敛至平衡点的缺点，本文采用一种新型快速终端滑模面［6］：

其中，ai，ci＞0，i＝1，2。结合分解控制，设计子系统A和子系统B的滑模面如下：

其中，0＜γ1＝p1／q1＜1，0＜γ2＝p2／q2＜1。p1、p2、q1、q2皆为正整数，且为奇数。注意到当（x1－z）＜0，x2＜0时，幂指数γ1，γ2使｜x1－z｜γ1∈R，｜x2｜γ2∈R，即不为虚数，因而不存在普通终端滑模所出现的奇异性问题。

当系统在滑动模态上时，有如下等式：

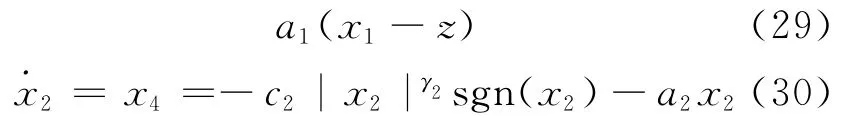
根据有限时间收敛的定义［9］，求解上述微分方程，得到各个子系统状态收敛的时间为：

其中，xz（0）为（x1－z）的初始值；x2（0）为x2的初始值。显然状态变量能在有限时间内收敛。

为了实现控制目的，同样使滑模面s1的导数等于0，即

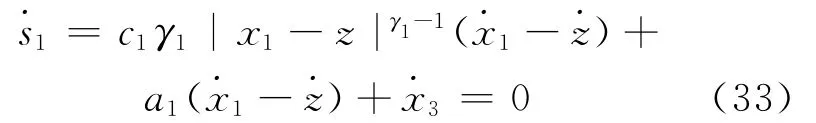
暂不考虑dθ，将（14）式代入（33）式可得系统的等效控制律为：

考虑到（17）式中间变量z的求导不易于实现而造成分解滑模等效控制量无法直接求出的问题，这里采用一种新型的具有反正切函数形式的中间变量［10］，即

同样，当s2→0时，有z→0。采用这样的形式，z的导数可以直接求得，有

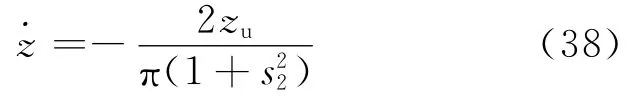
代入（36）式可得出控制律的具体表达式。

观察（31）式、（32）式可以发现，系统状态收敛至平衡点的时间与参数ai、γi、ci（i＝1，2）有关。其中当ci减小时，时间变长；ci增大时，时间缩短，但会影响跟踪的精确性。为了解决此矛盾，受文献［11］启发引入一维模糊推理来改善系统的性能，其原理如图2如示。

图2 模糊调节系数的原理图

图2中，li（i＝1，2，…，6）为选取参数。FC表示模糊推理系统，其输入语言变量为Xd（t），对应于变量＝｜lixi｜－，输出语言变量为C，对应于变量＝ci／li＋4，其中i＝1，2。模糊规则描述为：

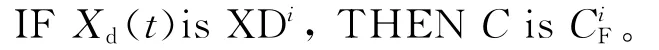
其中，XDi用来表示输入Xd（t）的模糊集｛NB，NM，NS，ZO，PS，PM，PB｝表示输出C 的模糊集｛VVS，VS，S，M，B，VB，VVB｝。模糊规则表见表1所列。模糊控制器采用Mamdani型模糊推理系统，其输入XDi的论域为［－1，1］，输出的论域为［0，2］。输入集和输出集的隶属函数采用均匀分布的三角形隶属函数，推理使用最大最小合成规则，解模糊采用重心法。

表1 模糊规则表

2.3 系统稳定性的证明

由于滑模面s2中的状态信息被转移到滑模面s1中，故下面来证明s1的稳定性。在系统的可控范围内，构造Lyapunov函数：

将（36）式代入，化简得：

因为k＞Dθ（t）／｜gθ｜，所以无论s1为何值，始终能保证˙V为非正数。这表明所设计的滑模面s1是渐进稳定的且能够在有限时间内到达。当子系统A处于滑动模态s1＝0时，有（x1－z）＝0以及x3＝0。另一方面，由（33）式得到：

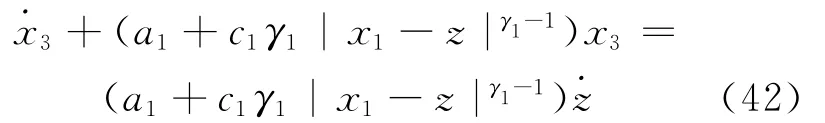
此方程可看作一个关于x3的一阶非齐次线性微分方程，对其求解得到：

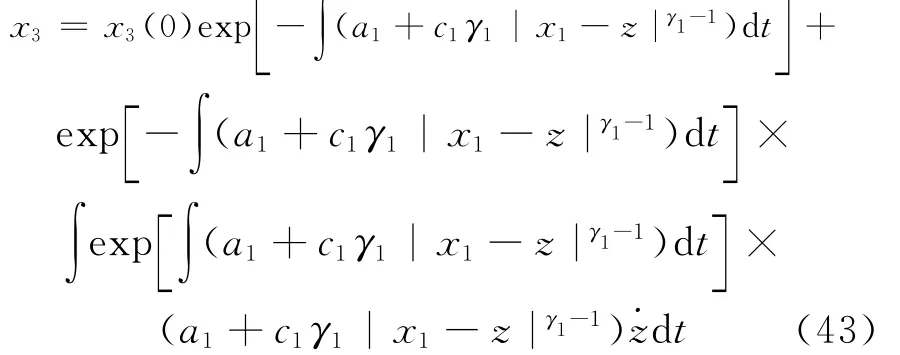
其中，x3（0）为x3的初始值。显然当（x1－z）＝0且＝0时，x3收敛为0。因此，当且仅当z→0（即s2→0）时，有x3→0。故2个子系统的稳定性都得到保证［3］。

3 仿 真

3.1 仿真参数选取

实际的模型参数为：

代入（12）式求得状态方程：

对于不确定参数JPθ、JR、JPδ所引起的系统的最大不确定矩阵为则不确定性干扰表示为其中，α为［－11］的随机数；分别为：

控制器的参数选取如下：c1＝2，c2＝0.5，γ1＝γ2＝29／31，l1＝l3＝0.5，l5＝2，l2＝l4＝0.5，l6＝0.5，k＝20，φ1＝5，φz＝15，a1＝0.3，a2＝0.1，zu＝0.8。

3.2 仿真结果及分析

选取下面3种情形的控制器进行仿真，滑模面分别选择为：

情形1 传统分解滑模面，即

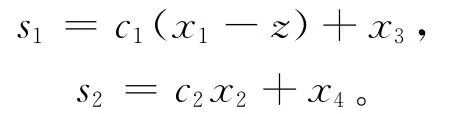
情形2 改进的传统分解滑模面，即

情形3 本文设计的分解滑模面，即

这里就两轮自平衡小车的摆角子系统平衡过程和位移子系统平衡过程进行仿真。假设系统的初始状态为：θP＝0.3，XRM＝0，ωP＝0，VRM＝0。即初始摆角为0.3rad（17°），位移、角速度、速度均为0。在整个过程中引入系统不确定性干扰IJ，摆角和位移趋近平衡过程的仿真曲线控制律的变化曲线如图3所示。

图3 系统摆杆角度、位移响应、控制律响应曲线

经模糊调节的滑模面系数曲线如图4所示。

图4 滑模面系数曲线

由图3a中摆杆的角度曲线可以看出，本文所设计方法的角度在3.6s时达到稳定，而传统分解滑模控制及其改进后的方法所需的时间分别大于9s和5s，因此本文设计的方法明显具有较快的动态响应速度；还可以看出其超调量较小，跟踪精度较高。图3b中位移曲线同样表明，本文所设计的方法响应速度较快，能将位移保持在较小的距离范围内。从图3c可以看出，系统的控制输入的响应速度也明显更快。图4体现小车在平衡过程中的变化情况，其到达稳定常值之前的变化表明了模糊推理系统产生的调节作用，反映了对系统性能实时改善的过程。

4 结束语

本文针对两轮自平衡车设计了一种新型控制方法。该方法将整个平衡控制系统分解为2个子系统，并分别定义了新型快速终端滑模面函数，利用可直接求导的中间变量实现1个控制量对小车的平衡控制，简化了高阶系统的设计，且能够使系统状态在有限时间内收敛至平衡点。在此基础上，运用模糊推理法调节滑模面系数，明显改善了动态响应速度。仿真结果也表明此控制方法能够获得较好的动态特性和具有较强的鲁棒性。

［1］刘金琨，孙富春.滑模变结构控制理论及其算法研究与进展［J］.控制理论与应用，2007，24（3）：407－408.

［2］Lo J C，Kuo Y H.Decoupled fuzzy sliding－mode control［J］.IEEE Trans Fuzzy System，1998，6（3）：426－435.

［3］Yongancloˇglu F，Kmrcgil H.Decoupled sliding－mode controller based on time－varing sliding surface for fourth－order systems［J］.Expert Systems with Applications，2010，37（10）：6764－6774.

［4］Zak M.Terminal attactors for addressable memory in neural networks［J］.Phys Lett A，1988，133（1－2）：18－22.

［5］Yu X，Man Z H.Fast terminal sliding－mode control design for nonlinear dynamic system［J］，IEEE Trans Circuits Syst I，2002，49（2）：261－264.

［6］Yu S，Yu X，Shirinzadeh B，Man Z.Continuous finite－time control for robotic manipulators with terminal sliding mode［J］.Automatica，2005，41（11）：1957－1964.

［7］张华宾.两轮移动式倒立摆机器人的研究［D］.合肥：中国科学技术大学，2007.

［8］杨兴明，杨传伟，马文森.一类欠驱动系统的全局改进积分模糊滑模控制［J］.合肥工业大学学报：自然科学版，2013，36（8）：923－928.

［9］Man Z H，Yu X H.Terminal sliding mode control of MIMO linear systems［C］／／Proceedings of the 35th Conference on Decision and Control.Kobe，Japan：IEEE Press，1996：4619－4620.

［10］于 涛，孙汉旭，贾庆轩，等.一类欠驱动系统的解耦滑模控制方法［J］.东南大学学报：自然科学版，2012，42：11－14.

［11］Yongancloˇglu F，Kmrcgil H.Single－input fuzzy－like moving sliding surface approach to the sliding mode control［J］.Electrical Engineering，2008，90（3）：199－207.