基于L曲线的自适应时空正则化视频超分辨率重建*

陈为龙，郭 黎

(1.四川师范大学数字媒体学院，成都610068;2.湖北民族学院信息工程学院，湖北恩施445000)

1 引言

目前对于空间域的超分辨率重建最为典型的有最大后验概率(MAP)[1]、迭代反投影(IBP)[2－3]、凸集投影(POCS)[4]等算法，文献[5 －6]也对超分辨率技术进行了研究。这些方法有效地提高了视频帧的配准精度，提升了视频重建效果，但是大多是基于理想的情况进行求解，这与超分辨率图像重建的实际应用是不完全符合的。在实际应用中，由于配准误差、噪声、低分辨率图像数量不足、退化模型估计误差等原因，使得超分辨率重建成为一个典型的病态问题。为了更有效地求解这类病态问题，通常在求解的过程中引入正则化的方法，利用解的先验知识构造附加约束，以确保解的存在、唯一和连续，从而把病态问题转成良态。大多数的正则化重建，正则化系数的估计都靠经验选取，很可能因为系数选取的不准确造成重建效果不理想。本文提出了一种基于L曲线的自适应正则化系数计算方法，可以通过算法自适应计算出正则化系数，提高了正则化系数选取的准确性。

2 超分辨率重建中的正则化

超分辨率重建是从已知的低分辨率图像序列{yk，k=1，2，…，m}中求出未知的高分辨率图像的过程，它是一个不适定的反问题，不满足Hadamard条件，即解的存在性、解的唯一性和解的连续性［7－8］。超分辨率重建中的低分辨率观测模型为

其中，X表示原始的高分辨率图像向量，y为低分辨率图像序列向量。将超分辨率重建的目标函数进行简化成为

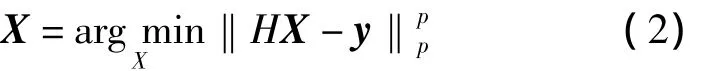
其中，‖·‖p为距离范数，高分辨率估计X是经排序后的Nx×1维列向量，低分辨率图像y是经排序后的Ny×1维列向量。超分辨率重建是一个逆向求解的问题，需要加入一个惩罚函数来抑制噪声等的影响，加入惩罚函数的方法就是正则化。加入正则化项的超分辨率重建如式(3)所示:

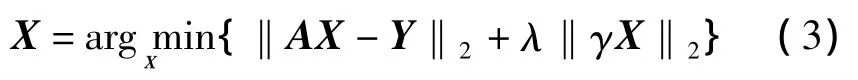
式中，‖AX－Y‖2是数据拟合项，代表数据的相似性;‖γX‖2为正则化项，它在一定程度上控制解的扰动;λ是正则化系数，它用来平衡上式中的第一项(数据拟合项)和第二项(正则化项)在求解中的贡献，通常为标量。当λ值增加，会使重建图像的平滑度增大。在低分辨率图像数量不足、运动估计存在误差以及存在噪声等情况下，较大的λ值能够有效提高重建图像的质量。但同时，对λ的取值不能过大，否则容易造成重建图像过于平滑。常用的正则化方法主要有 Tikhonov正则化［9－10］、截断奇异值分解正则化等方法［11－12］。

3 基于L曲线的自适应时空正则化视频超分辨率重建

为解决超分辨率重建中的病态问题，在超分辨率重建中通常引入空间正则化算子来得到较为精确的解，避免重建过程中放大噪声以及出现空间振铃现象。对于视频而言，除了空间信息，视频各帧在时间上也存在帧间相关信息。因此，本文在视频超分辨率重建中引入时空联合正则化算子，通过图像本身的空间平滑信息和视频相邻帧的帧间相关先验信息的引入，有效提高解的质量。另外，在正则化重建中通过L曲线自适应计算得到最合适的正则化系数，由此得到较好的重建结果。

3.1 时空正则化算子的提出

为了更好地利用视频的时空联合特性，提出了时空联合正则化算子Γ，重建的代价函数如式(4):

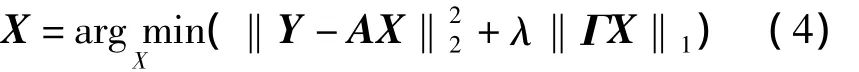
式中，Y是输入的低分辨率视频帧序列，A是重建的权值矩阵，Γ是正则化算子，X代表重建后的高分辨率视频序列，λ是时空联合正则化系数。此目标函数中将L1范数和L2范数联合起来使用，第一项(数据拟合项)中的L2范数用于加强对于数据重建的真实度;第二项(正则化项)采用L1范数用于提高梯度域的稀疏性，产生在时间和空间上更锐化的边缘并且避免振铃效应。其中，时空联合正则化算子Γ如下:

3.2 基于L曲线的正则化系数的确定

在超分辨率重建过程中引入的正则化方法都包含对数据忠实性的一种折衷考虑，因此，在式(3)中的正则化系数λ是可变的。如何确定一个最优的λ就是需要解决的问题。事实上，当λ变化时，关于λ‖γX‖2对于‖AX－Y‖2可以在lg－lg尺度上得到图形的表示，这种图形表示的曲线称为L曲线［13］。特别注意的是，λ是一个沿着这条曲线的参数。

在L曲线水平和垂直部分相交的地方有一个拐点，此处定义了过正则化和欠正则化的合理过渡，即在这两种极端情况下的一种合理平衡，该拐点处对应的正则化系数λ的值则是最合适的正则化系数的数值。图1中，在曲线上对应拐点处的最合适的正则化系数用λ*来表示。λ*通常采用如下定义，即用于表示优化的λ必须等于下面曲率函数的最大值:

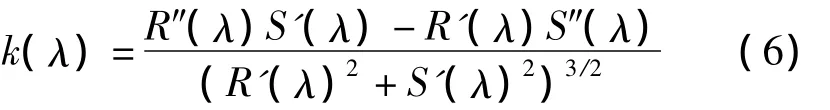
式中，R(λ)=lg‖γX(λ)‖2，S(λ)=lg‖AX － Y‖2。

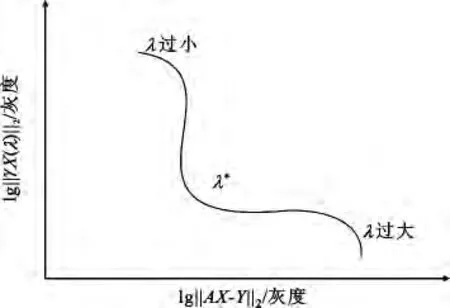
图1 L_Curve示意图Fig.1 The L_Curve diagram

3.3 本文算法的提出

基于前面的分析，本文所提出的基于L曲线的自适应时空正则化超分辨率重建算法步骤描述如下(其中，Framenum是低分辨率视频的总帧数):

Step 1:令i=1(当前要重建的是低分辨率视频的第i帧);

Step 2:对当前的i和j(此处的j=i…i+num，是参与此次重建的所有高分辨率帧的编号)进行如下操作;

Step 3:输入低分辨率视频中的图像序列构成向量Y;

Step 4:构造每个高分辨率像素点对每个低分辨率像素点的相对贡献权值，即构造稀疏矩阵A;

Step 5:构造正则化矩阵Γ;

Step 6:根据 Y、A、Γ，采用3.2 节的方法计算出当前i对应的最合适的正则化系数λ;并把Y、A、Γ和λ代入式(4)，计算得到X;

Step 7:因为X中包含了num帧高分辨率帧的信息，取第i帧高分辨率帧对应的信息，得到Xi即为重建后的第i帧高分辨率帧(其中，num是参与时空正则化的帧数，num越大，时间正则化越明显;num越小，时间正则化越弱。本文中取num=2);

Step 8:i=i+1。当i=Framenum时停止，得到重建的高分辨率视频;否则，继续Step 2～Step 8。

4 实验

为了更好地证明算法的有效性，我们采用如下一系列的实验来进行验证。实验中，我们将基于稀疏矩阵的自适应时空正则化重建的结果分别与双三次插值、正则化系数过大的重建结果和正则化系数过小的重建结果进行对比。本文实验平台为Win7 64位操作系统，Matlab2010版本，英特尔赛扬双核处理器(2.6 GHz)，4 GB内存。

4.1 模拟视频序列重建实验

首先对模拟的多幅低分辨率图像序列进行超分辨率重建，本实验使用了字母图像进行实验。首先对图像进行平移和旋转产生10幅低分辨率观测图像，然后对模拟的图像序列采用大小为7×7、方差为0.5的高斯点扩展函数进行空间模糊，再进行2倍的空间下采样，然后加入信噪比为40 dB的随机噪声，并将它们作为观测得到的低分辨率图像序列。对该模拟图像序列进行2倍超分辨率重建，取出第6帧的重建结果如图2所示。

图2 重建视频的第6帧Fig.2 The 6th frame in reconstructed video sequence

图2 中(a)为原始高分辨率的图像，(b)为模拟低分辨率序列的第6帧，(c)为双三次2倍插值放大的结果，(d)为正则化系数过小的超分辨率重建结果(λ=0.000 5)，(e)是正则化系数过大的超分辨率重建结果(λ=0.003)，(f)为自适应时空正则化超分辨率重建结果(λ =0.001 7)，(g)、(h)、(i)和(j)分别为(c)、(d)、(e)和(f)的局部放大图。从实验结果可以看到，双三次插值和正则化系数过大的重建结果都很模糊，正则化系数过小，导致图像太过锐化，字母和其他形状边缘会有明显的振铃效应(字母或其他图像的边缘处有明显的高亮区域)。采用本文提出的算法计算得到的正则化系数，可以得到更好的重建效果。图3是重建序列第6帧时得到的L曲线图及最优的正则化系数值。

图3 重建视频第6帧时的L曲线Fig.3 The L_Curve of the SR reconstruction(the 6th frame)

4.2 真实视频序列重建实验

采用“MissAmerica”视频序列，图4中(a)和(b)分别是该视频序列的第1帧和第12帧。

我们对输入的低分辨率视频序列进行2倍的空间重建，效果对比如图4所示。其中，(c)是对视频序列第1帧双线性2倍插值放大的结果，(d)为正则化系数过小的超分辨率重建结果(λ=0.000 8)，(e)是正则化系数过大的超分辨率重建结果(λ=0.003 6)，(f)为自适应时空正则化超分辨率重建结果(λ=0.001 9)，(g)～(j)是对视频序列第 12帧的实验结果。

图4 重建视频的部分帧Fig.4 Some frames in reconstructed video sequence

从实验结果可以看到，双三次插值和正则化系数过大的重建结果都很模糊。正则化系数过小，导致图像太过锐化，图像中多处有明显的振铃现象。基于L曲线的自适应时空正则化重建结果则明显好于其他几种方法。图5(a)和(b)是重建序列第1帧和第12帧时得到的L曲线图及最优的正则化系数值。

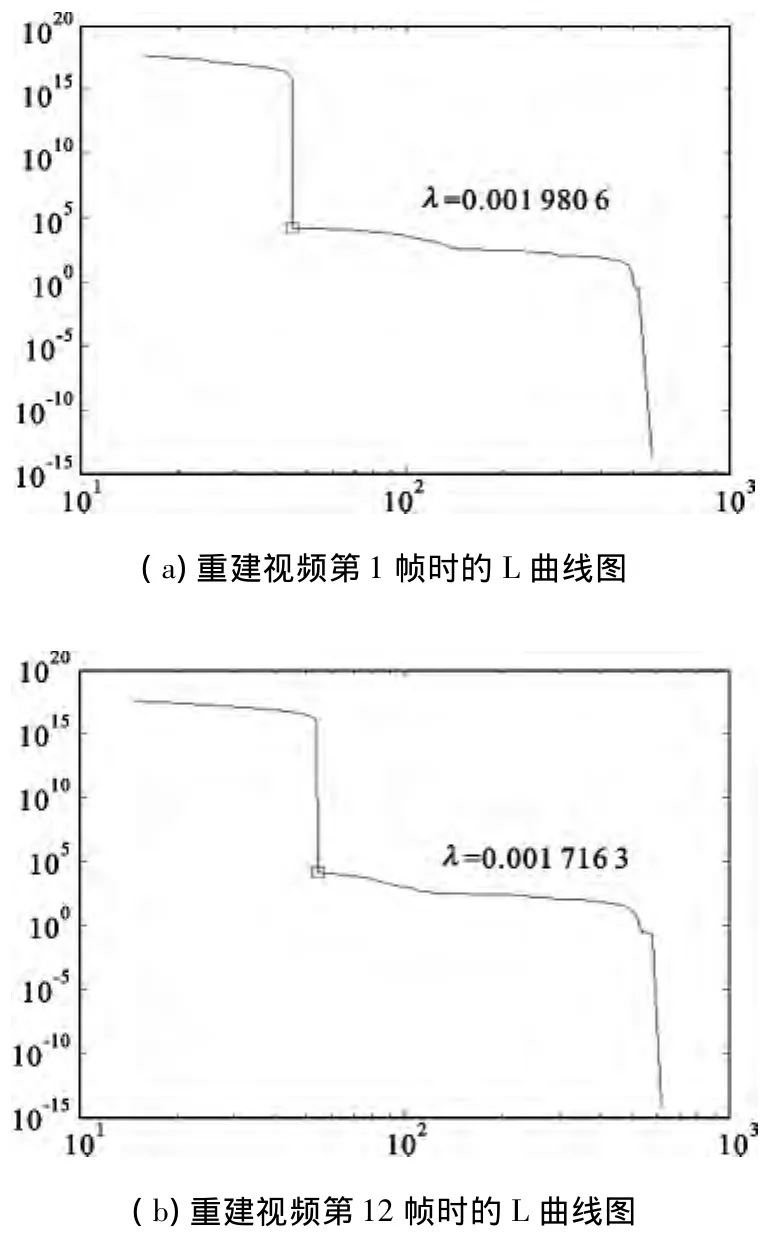
图5 重建视频得到的L曲线图Fig.5 The L_Curve of the SR reconstruction(the 1st and 6th frame)

5 总结

为解决超分辨率重建的病态问题，提高解的稳定性，必须引入正则化的方法。在正则化重建过程中，正则化系数的确定是一个难点:过大的正则化系数会导致重建图像过度平滑;正则化系数过小，又可能会导致图像的过度锐化，也不能有效克服噪声等因素对重建效果的影响。本文根据不同算子所具有的特点，并结合视频序列的时间特性，在重建过程中引入了时空正则化算子。同时，算法中提出了一种基于L曲线的自适应时空正则化系数计算方法，用以自动计算出最优的正则化系数。通过模拟视频序列和真实视频序列的重建实验证明了所提算法的有效性。

使用基于L曲线的方法可以自动计算得到合适的正则化系数，有效地解决了如何确定正则化系数这一难点问题。但因为基于L曲线的方法本质是在数据项和正则化项之间寻找一种数值折衷，是基于数值的客观分析，再考虑到不同的图像给人的视觉感受不同等因素，该方法并不能保证对所有的视频重建都能得到最优的视觉效果，但基于L曲线的方法对绝大多数的重建效果都是优异的。

[1]Shen H F，Zhang L P，Huang B，et al.A map approach for joint Motion estimation segmentation，and super resolution[J].IEEE Transactions on Image Processing，2007，16(2):479－490.

[2]Irani M，Peleg S.Motion analysis for image enhancement resolution，occlusion，and transparency [J].Journal of Visual Common Image Represent，1993(4):324 －335.

[3]曹聚亮，吕海宝，谭晓波，等.基于实时帧迭代反投影算法的图像序列超分辨率处理[J].光学技术，2004，30(5):558－563.CAO Ju － liang，LV Hai－ bao，TAN Xiao － bo，et al.Superresolution of image sequences based on real－time frame iterative back － projection algorithm[J].Optical Technique，2004，30(5):558 －563.(in Chinese)

[4]范冲，龚健雅，朱建军.一种基于去混叠影像配准方法的POCS超分辨率序列图像重建[J].测绘学报，2006，35(11):358 －363.FAN Chong，GONG Jian － ya，ZHU Jian － jun.POCS Super－resolution Sequence Image Reconstruction Based on Image Registration Excluded Aliased Frequency Domain[J].Acta GeodaetICA et Cartographica Sinica，2006，35(11):358 －363.(in Chinese)

[5]张进，王仲，李雅洁，等.高精度影像测量系统中图像的超分辨率重建[J].光学精密工程，2011，19(1):168 －174.ZHANG Jin，WANG Zhong，LI Ya － jie，et al.Super－ resolution reconstruction of image in high accuracy image measuring system[J].Optics and Precision Engineering，2011，19(1):168 －174.(in Chinese)

[6]Chen W L，He X H，Song H Y.An improved sequence －to－sequence alignment method combined with featurebased image registration algorithm[J].Journal of Information Science and Engineering，2012，28(3):617 －630.

[7]Borman S.Topics on multiframe superresolution restoration[D].Indiana，IN:University of Notre Dame，2004.

[8]Guo K，Yang X，Zha H，et al.Multiscale semilocal interpolation with antialiasing[J].IEEE Transactions on Image Processing，2012，21(2):615 －625.

[9]Chung J，Eldad N，James N.Numerical methods for coupled super － resolution[J].Inverse Problems，2006，22(4):1261－1272.

[10]商俊国，焦斌亮.多帧图像的Tikhonov正则化重建算法研究[J].计算机应用研究，2011，28(2):785 －791.SHANG Jun － guo，JIAO Bin － liang.Research on Tikhonov regularization multiframe images reconstruction algorithm[J].Application Research of Computers，2011，28(2):785 －791.(in Chinese)

[11]Vogel C R.Computational methods for inverse problems[M].Philadelphia:SIAM，2002:97－126.

[12]Bovik A C.Handbook of image and video processing[M].London:Academic Press，2009:141 －160.

[13]王宏志，赵爽，胡艳君.基于L－曲线正则化的MAP超分辨率图像复原[J].吉林大学学报(理学版)，2008，46(2):275 －278.WANG Hong － zhi，ZHAO Shang，HU Yan － jun.Super－resolution on Image Resolution with MAP Based on L－ Curve[J].Journal of Jilin University(Science Edition)，2008，46(2):275 －278.(in Chinese)