镍微合金化9310钢的高温热变形行为

张志正，王春旭，黄顺喆，厉 勇，刘宪民，周晓龙

（1.昆明理工大学材料科学与工程学院，昆明 650093；2.钢铁研究总院特殊钢研究所，北京 100081）

0 引 言

9310钢是国内外广泛使用的一种低成本轴类用高强度渗碳钢，具有优良的综合性能，如强度高、韧性好、淬透性和焊接性较好，多用于制造截面尺寸较大且受重载荷的传动构件，如航空领域中的关键齿轮、齿轮轴、主旋翼轴、尾桨轴等［1］。目前国内外对9310钢的研究较多，主要集中在奥氏体冷却转变和晶粒长大行为、组织和性能以及高温热变形行为等方面［2－5］，而将镍微合金化技术应用于9310钢的相关研究还鲜见报道。作者采用Gleeble-3800型热模拟试验机对真空感应熔炼镍微合金化9310钢的热变形行为进行了研究，为其工业化试制提供技术支持。

1 试样制备与试验方法

试验用镍微合金化9310钢（以下简称试验钢）采用真空感应冶炼，其化学成分为（质量分数/%）0.12C，1.21Cr，3.24Ni，0.11Mo，0.66Mn，0.26Si，0.017Nb，余Fe。钢锭经高温扩散退火后，锻造成型，然后加工成尺寸为φ10mm×15mm的压缩试样。轴向压缩试验在Gleeble-3800型热模拟试验机上进行，试样先以10℃·s－1的加热速率加热到1 473K，保温5min后再以10℃·s－1的冷却速率冷却到变形温度，保温5s后进行压缩变形。变形温度分别为1 173，1 273，1 373，1 473K，变形速率分别为0.01，0.1，1，10s－1，最大真应变为0.9，变形后立刻喷水淬火，以便分析其高温组织。用线切割机把热压缩试样沿压缩方向从中间剖开，磨平、抛光后，使用腐蚀液（饱和苦味酸＋少量海鸥洗剂灵的混合溶液）腐蚀奥氏体晶界，用光学显微镜观察显微组织。

2 试验结果与讨论

2.1 高温流变曲线及变形组织

从图1中可以看出，在不同的变形条件下，试验钢的高温流变曲线表现为动态回复型和动态再结晶型［6］两种类型。在试验范围内，动态再结晶只在较高的变形温度和较低的应变速率条件下发生。在高温变形过程中，试验钢的流变应力随着变形温度的降低和应变速率的增大而提高。在相同应变速率下，变形温度越高，动态软化速率越快，因而动态软化程度越大，峰值应力和稳态流变应力逐渐降低，峰值应变也随着变形温度的升高而逐渐减小。而在相同的变形温度下，随着应变速率的增加，试验钢的加工硬化率提高，峰值应力和稳态流变应力也随之升高。当应变速率为0.01s－1、变形温度高于1 173K时，试验钢的流变曲线就表现为动态再结晶型；而当应变速率提高至0.1s－1和1s－1，变形温度分别在1 273～1 473K和1 373～1 473K时，试验钢的高温流变曲线才表现为动态再结晶型；而当变形速率达到10s－1时，在试验温度范围内，试验钢的高温流变曲线只表现为动态回复型。然而金属在高温变形过程中是否发生了动态再结晶，单从高温流变曲线上还不能完全断定，必须借助于相应的显微组织加以分析确认。

从图2可以看出，变形前试验钢奥氏体晶粒平均尺寸约为70μm。从图3可以看出，应变速率为0.01s－1、变形温度为1 173K 时，试验钢组织大部分为拉长的条状变形晶粒，此时试验钢在变形过程中未发生动态再结晶，只发生动态回复；当变形温度高于1 173K后，显微组织均为动态再结晶晶粒，并且随着变形温度的升高，晶粒发生长大。

图1 试验钢在不同变形条件下的高温流变曲线Fig.1 High temperature flow stress curves of test steel under different deformation conditions

同样，应变速率为0.1s－1，变形温度为1 173K时，试验钢组织（图略）主要为变形晶粒，在变形过程中发生动态回复，当变形温度高于1 173K后组织表现为动态再结晶。应变速率为1s－1的试验钢组织（图略）表明，变形温度为1 173K时，试验钢只发生了动态回复，当变形温度升高至1 273K后，组织为动态再结晶晶粒，这与相应的高温流变曲线特征存在差别。应变速率为10s－1试验钢组织（图略）表明，变形温度只要高于1 273K，试验钢就可以发生动态再结晶，与高温流变曲线特征明显不同。这可能与9310钢添加镍后的加工硬化率的变化有关。具有较高加工硬化率的金属在高温变形过程中往往会出现部分动态再结晶，但所产生的软化不足以抵消加工硬化，此时即使发生了动态再结晶，在高温流变曲线上也不会表现出动态再结晶的明显特征，必须通过组织观察分析来确定。

图2 变形前试验钢显微组织Fig.2 Microstructure of test steel before deformation

2.2 热变形方程

金属材料的高温流变应力既与材料化学成分有关，又与变形温度T、应变速率ε·以及应变ε有关，当材料成分不变时，流变应力σ与变形条件之间具有如下的双曲正弦关系［7－8］：

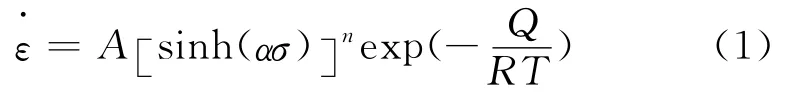
式中：σ为峰值应力σp成稳定状态流变应力σs，或相应于某指定应变量的流变应力，此处σ采用峰值应力σp；R为气体常数；Q为控制软化过程的激活能；A，n，α为相关常数。

在低应力时，式（1）可简化为

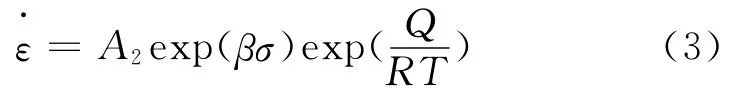
其中，常数α，β及n′之间满足α＝β/n′。对式（2）和（3）两边分别取对数并整理得到：

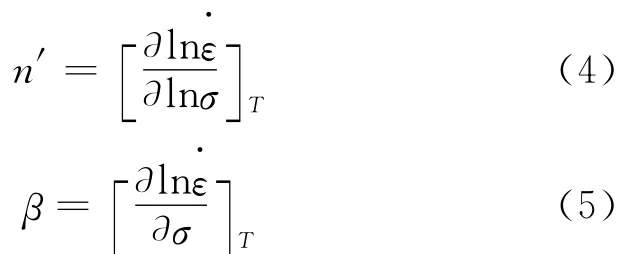
在高应力时，式（1）可简化为

图3 应变速率为0.01s－1时不同变形温度下试验钢的显微组织Fig.3 Microstructure of test steel after deformation at different temperatures with stain rate of 0.01s－1

将图1的真应力－应变曲线数据按式（4）和（5）处理得到峰值应力－应变速率关系曲线，如图4所示。从图中可以看出和都近似呈线性关系，通过线性回归分析可得，β＝0.072 75MPa－1和n′＝7.736 4，进而计算得α＝β/n′≈0.009 403 9。

对式（1）两边取自然对数得：

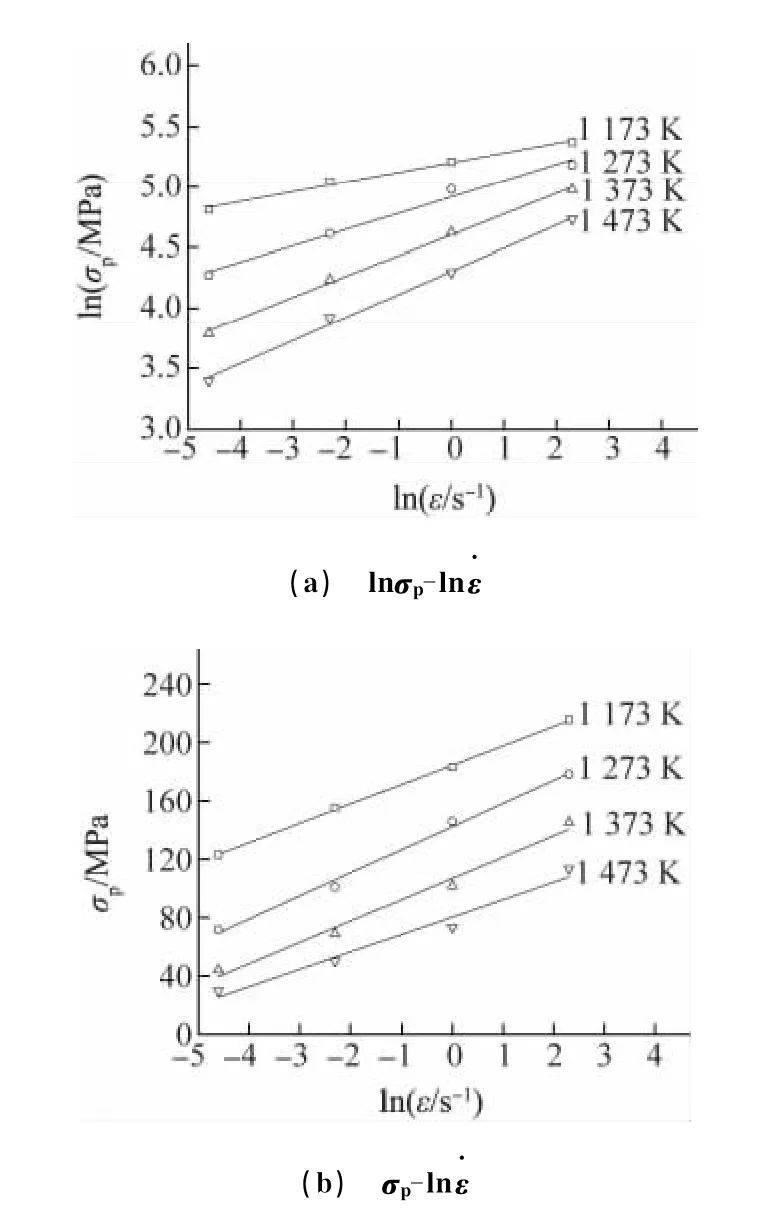
图4 峰值应力与应变速率的关系Fig.4 Relationship between peak stress and strain rate

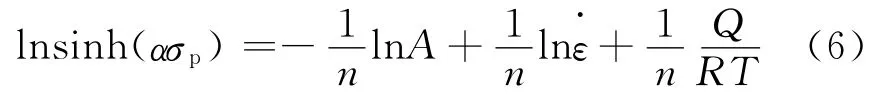
当变形温度恒定时，式（6）两边对应变速率求偏导，得：

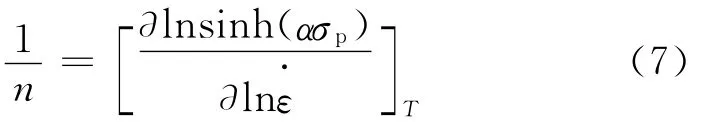
当应变速率恒定时，式（6）两边对1/T求偏导，得：

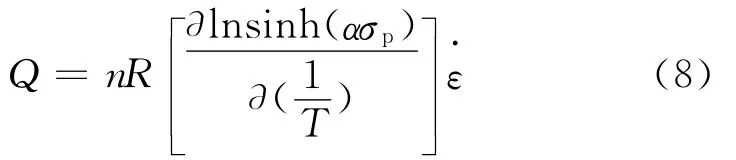
根据图1中的高温流变曲线数据，可得峰值应力与应变速率和变形温度之间的关系曲线，如图5所示。通过线性回归，可得出：A＝9.072 06×1017；n＝5.512 7；Q＝362.649kJ·mol－1。将上述结果代入式（1）中，可以确立镍微合金化9310钢的热变形方程为

2.3 Zener-Hollomon因子

参数（Zener-Hollomon因子）被广泛用以表征变形温度及应变速率对热变形过程的综合作用。在热变形过程中有如下关系式［9］：

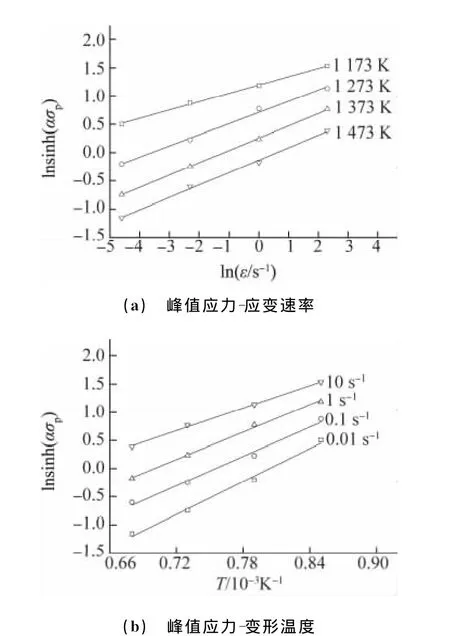
图5 峰值应力与应变速率和变形温度的关系Fig.5 Relationships between peak stress and strain rate（a）and deformation temperature（b）

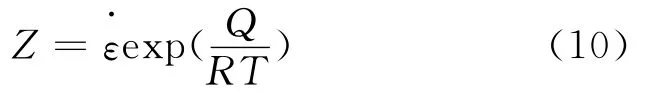
将式（10）带入式（1）中可得：

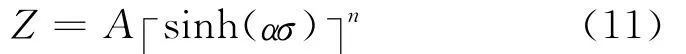
故由式（9）可得试验钢的参数表达式为

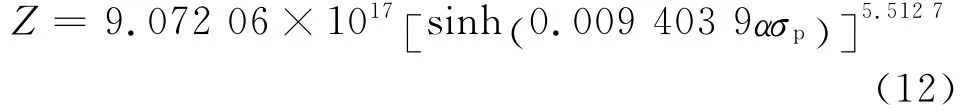
通过已求得的热变形激活能，便可以计算得到不同变形条件下试验钢的Z参数。可以看出，随着Z值的增加，试验钢热变形过程中的峰值应力相应增加，且lnZ与lnsinh（ασp）呈线性关系，相关系数可达到0.99，如图6（a）所示，根据参考文献［10］中的处理方法，得到σp与Z参数的关系式（13），如图6（b）所示。

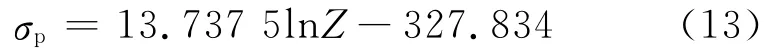
3 结 论

（1）镍微合金化9310钢的流变应力和峰值应变随着变形温度的升高和应变速率的降低而减小；试验钢在真应变为0.9，应变速率为0.01～10s－1的条件下，随着变形速率的提高，其发生完全动态再结晶的温度也逐渐升高。

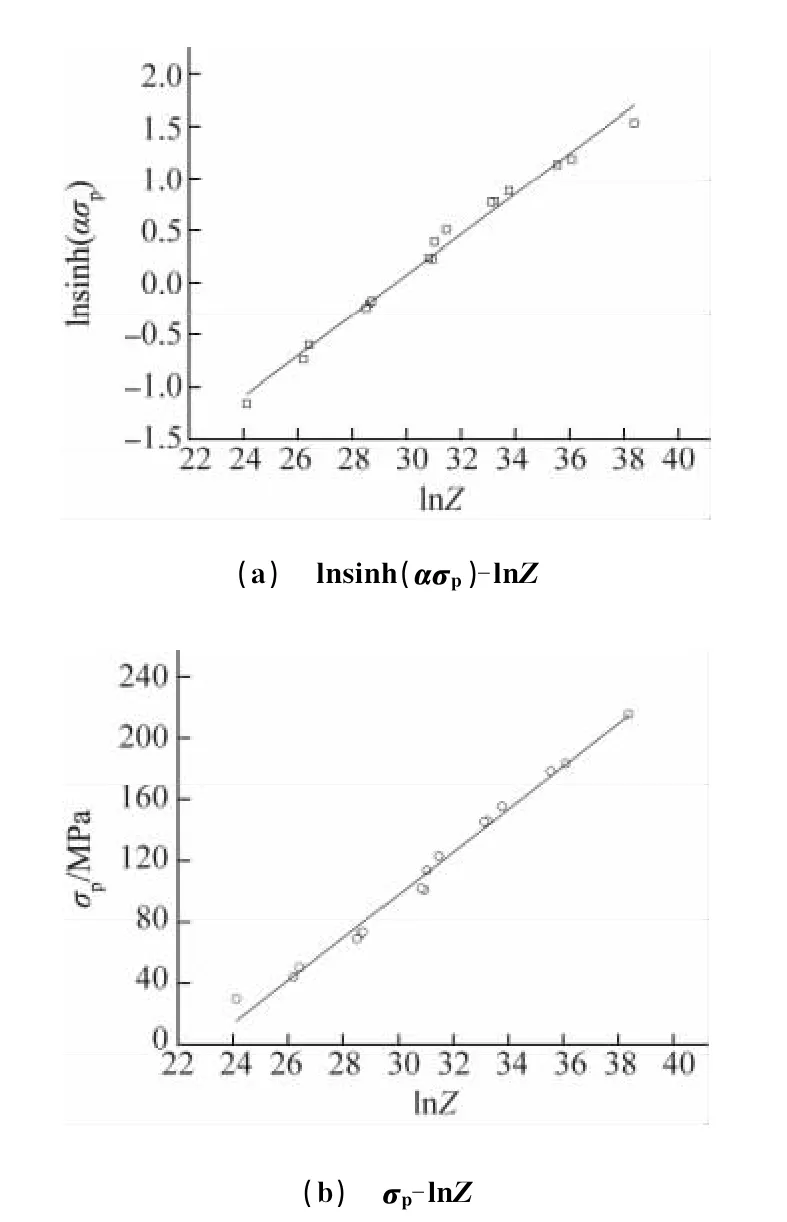
图6 lnsinh（ασp）-lnZ和σp－lnZ的关系曲线Fig.6 Relationship of lnsinh（ασp）-lnZ （a）and relationship ofσp－lnZ （b）

（2）镍微合金化9310钢的热变形激活能为362.649kJ·mol－1，并得到了其热变形方程。

［1］周凤云，李熙章.高强度渗碳钢制构件的断裂分析［J］.理化检验-物理分册，2003，39（4）：206-209.

［2］刘安武，厉勇，王春旭，等.SAE9310钢热变形行为的研究［J］.钢铁，2009，44（10）：82-86.

［3］吴秋平，王春旭，刘宪民，等.回火温度对9310钢力学性能及组织的影响［J］.热加工工艺，2012，41（6）：179-183.

［4］黄顺喆，厉勇，王春旭，等.9310钢的奥氏体晶粒长大规律研究［J］.热加工工艺，2010，39（18）：31-33.

［5］厉勇，王春旭，刘宪民，等.SAE9310钢奥氏体的冷却转变行为［J］.机械工程材料，2010，34（5）：12-15.

［6］SELLARS C M.Recrystallization of metals［J］.Metals Forum，1981，4（1/2）：75-80.

［7］FARAG MM，SELLARS C M.Flow stress in hot extrusion of commercial-purity aluminum［J］.Journal of the Institute of Metals，1973，101（5）：137-145.

［8］JONAS J J，SELLARS C M，TEGART WJ.Strength and structure under hot working conditions［J］.Int Met Rev，1969，130（14）：1-24.

［9］MEDINA S F，HERNANDEZ C A.General expression of Zener-Hollomon parameter as a function of the chemical composition of low alloy and microally steels［J］.Acta Materialia，1996，44（1）：137-148.

［10］张斌，张鸿冰.20crMnTi结构钢热变形行为及其数学模型［J］.上海交通大学学报，2003，37（12）：1826-1830.