非对称变宽度斜拉桥力学性能分析

孙建渊,王 灏,陈方东

（1.同济大学桥梁工程系，上海市 200092；2.浙江省交通规划设计研究院，浙江杭州 310006）

0 引言

双塔三跨式斜拉桥是斜拉桥中最常见的结构布置形式，在国内外已经建成的斜拉桥中，这种方案得到广泛的应用。从简化设计、方便施工考虑，双塔三跨式斜拉桥以对称布置居多[1]。所谓对称布置，指的是斜拉桥的立面形状和平面形状经对称后能够完全重合；若不能完全重合，则为非对称的布置形式。在实际工程中，由于通航要求、地形、水文条件的复杂性以及设计、施工上的要求，双塔三跨式斜拉桥采用非对称结构布置的情况也十分常见。日本多多罗大桥由于地形因素限制，在立面上采用两边跨不相等的非对称布置[2]。葡萄牙学者A.J.Reis论述了非对称斜拉桥的结构概念，将非对称性的形成原因归纳为拉索和平曲线的不对称，并列举了诸多实例[3]。此外，为获得合理经济的桥跨布局和处理观赏效果的环境要求时，重庆的涪陵乌江二桥和国外的Erasumus桥采用了非对称的桥塔布置[4，5]。

除了上述情形，斜拉桥主梁宽度的改变也会形成非对称结构布置。通常为了设计和施工的简便，斜拉桥主梁宽度保持一致，但在设计公路和城市道路互通式立交桥中，由于加减速车道的存在，要求主梁的宽度进行变化[6]。世界上第一座非对称变宽度斜拉桥是我国郑州市中心区铁路跨线桥[7]。为了更好地了解非对称变宽度斜拉桥的力学性能，本文以某双塔三跨式变宽度结合梁斜拉桥为研究背景，采用有限元软件对该桥建立分析计算模型，研究变宽度主梁的非对称性对斜拉桥主梁、桥塔及拉索的影响，并提出适合于非对称变宽度斜拉桥的设计思路。这将丰富我国斜拉桥设计理论，填补非对称斜拉桥研究的空白，具有较高的学术价值与设计指导意义。

1 工程概况

某双塔三跨式单索面结合梁斜拉桥，跨径布置为57 m+108 m+340 m+108 m+57 m＝670 m，采用半漂浮体系。两座混凝土主塔为钻石形，承台以上高为116 m，桥面以上高约91 m。斜拉索采用中央索面布置，索面间距2.0 m，梁上标准索间距为8.0 m。主塔、辅助墩及边墩在竖向和横桥向约束主梁，顺桥向容许主梁滑动。

钢-混凝土结合主梁采用单箱三室箱形截面，梁高3.5 m。根据主梁宽度的不同，斜拉桥结构可划分为标准段与变宽段，如图1所示。标准段长505 m，位置从一侧边跨延伸至另一侧桥塔B处，在此范围内主梁宽度保持不变，为26.0 m；从桥塔B处开始，主梁宽度线性增加至34.5 m，之后保持不变，渐变部分的长度为70 m，整个变宽度长度为165 m。该斜拉桥左右两边跨的主梁形式完全不同，在结构体系上成为非对称变宽度的斜拉桥。

图1 总体立面布置图(单位：m)

2 有限元计算模型

主桥静力计算采用通用空间结构分析计算软件Midas来建立空间有限元模型。主梁、桥塔采用空间梁单元模拟，斜拉索采用桁架单元模拟。边界条件为：主梁与主塔、辅助墩之间均为竖向、侧向约束，纵向自由的约束形式；塔底与承台固接。有限元计算模型的总体坐标系以顺桥向为X轴，以横桥向为Y轴，以竖向为Z轴。全桥共计408个节点，梁单元共232个，桁架单元共152个，有限元模型如图2所示。

图2 有限元模型图

利用Midas进行合理成桥索力的确定，模型中应考虑结构自重、二期恒载、斜拉索的初拉力、桥面板中钢束的预应力，此时斜拉索的初拉力宜取为单位力（1 kN），这样可通过程序生成结构的影响矩阵。索力确定采用零位移法，同时引入能够构成满足控制要求的不平衡条件，将竖向位移量控制在一个很小的范围内，进行静力线性分析后，利用MIDAS中的“未知荷载系数”功能，设定索力调整后桥梁结构应满足的约束条件，在程序中通过影响矩阵求出初始索力值[8]。在计算中，采用桁架单元模拟斜拉索构件，以保证拉索的荷载效应为线性叠加，从而满足影响矩阵的使用条件[9]，同时采用等效弹性模量反映斜拉索的垂度效应。

3 计算结果及分析

在Midas中通过未知荷载系数法，限制斜拉索与主梁交点处的位移上下限为±5mm，同时控制桥塔、桥塔处主梁的弯矩分布，得到一组索力值。在此索力分布下，研究非对称变宽度的主梁对斜拉索、主梁和桥塔受力性能的影响，得到非对称变宽度斜拉桥结构的力学性能。

图3、图4分别给出了标准侧与变宽侧边跨、中跨斜拉索索力的对比情况。可以看出，斜拉索索力分布呈现明显的非对称性。边跨斜拉索索力具有如下分布特点：变宽侧索力在主梁宽度渐变段要高于标准侧主梁，而在主梁宽度不再变化后，变宽侧索力有所下降，并低于标准侧对应拉索的索力；在宽度变化一侧，端部拉索的索力要高于标准侧。这种边跨索力具有峰谷错位特点的分布不同于常规对称结构的索力分布，其原因主要是由于变宽侧主梁自重与刚度的增加。中跨斜拉索索力分布的变化没有边跨明显，除了靠近桥塔的几根拉索，两侧的索力相差不大，分布形式也较为接近。

图3 两边跨斜拉索索力对比图

图4 两中跨斜拉索索力对比图

另外，在斜拉索索力调整过程中发现，当主梁通过索力调整达到合理状态时，变宽侧不对称的索力分布在主塔上产生不平衡的水平分力，使得主塔上出现较大的弯矩。为了降低桥塔弯矩，只能通过降低索力，缩小两侧不平衡力的差距，但与此同时，主梁上的弯矩又有所增加。因此，对于非对称变宽度斜拉桥结构来说，通过索力调整无法使得主梁与桥塔同时处于一个较为合理的受力状态，只能兼顾两者的内力分布，在安全、经济合理的条件下，充分考虑结构构件的承载能力，优化承载构件的内力状态。采用对称布置形式的斜拉桥，其索力调整较为方便，因为在设计时通常要求边跨与中跨的重量相当，即结构处于整体平衡的状态，桥塔几乎不承受不平衡水平力[10]；而对于非对称变宽度斜拉桥，由于边跨主梁重量的增加，整体平衡被打破，需要考虑非对称引起的索力变化对结构的影响。合理的索力优化是使这一特殊结构达到理想受力状态的主要内容，应在桥梁施工期确定理想安装索力以及控制理想成桥状态索力。

图5为永久荷载作用下，非对称变宽度斜拉桥结构的主梁弯矩图。

图5中主梁的弯矩分布呈现明显的非对称性。在斜拉索索力作用下，主梁上的弯矩除了变宽侧桥塔、辅助墩支点及端部外，都处于一个较小的分布范围内。变宽侧主梁自重的增大以及刚度的增加，使得变宽侧的弯矩分布较为复杂。考虑到结合梁截面适合于承担较大的正弯矩，对于主梁端部的内力分布还是可以接受的；而对于辅助墩位置处较大的负弯矩，应通过配置桥面板内预应力筋的方式予以解决。

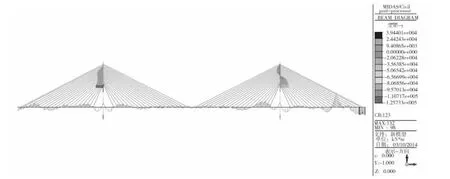
图5 永久荷载作用下主梁弯矩图

永久荷载作用下的斜拉桥结构，在斜拉索张拉力的作用下，处于合理的成桥状态，主梁的线型就是设计标高，因此结构的变形及刚度应当根据汽车荷载作用下的结果进行分析。图6、图7为结构在汽车荷载作用下位移包络图与弯矩包络图。由于变宽侧主梁竖向刚度的增加，汽车荷载引起的位移要小于标准侧主梁。主梁弯矩分布也具有一定的非对称性：变宽侧的弯矩要比标准侧的大。根据结构力学基本原理，由于主梁尺寸的增大，使变宽侧主梁刚度提高，进而分担的内力也有所增加。不过，在主梁构造参数中仅为宽度发生变化，而梁高保持不变，其竖向抗弯刚度增加程度相比标准侧主梁并不明显，因此引起的主梁内力变化较小，主梁弯矩分布接近于对称的形式。

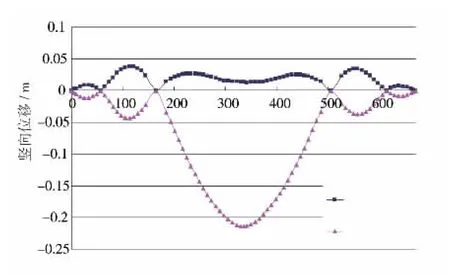
图6 汽车荷载作用下主梁位移包络图

图8为斜拉桥桥塔在永久荷载作用下的弯矩图。变宽侧桥塔弯矩分布与标准侧呈现明显的区别。在斜拉索集中的塔上部，两桥塔的弯矩方向截然相反，这与图3所示的索力分布有着密切的关系。在桥塔中下部，变宽侧桥塔的弯矩比标准侧大，相差幅度在14%左右。

图7 汽车荷载作用下主梁弯矩包络图

图8 汽车荷载作用下主梁弯矩包络图

图9～图12为斜拉桥桥塔在汽车荷载作用下的位移与弯矩包络图。由于两座桥塔采用相同的截面构造，在汽车荷载作用下，其水平位移包络图与弯矩包络图接近对称。虽然结构的非对称性使得变宽侧的位移与弯矩略大于标准侧，但变宽侧主梁刚度提高幅度不大，因此这种差异性并不明显，可忽略其影响。

图9 汽车荷载作用下标准侧桥塔位移包络图

图10 汽车荷载作用下变宽侧桥塔位移包络图

图11 汽车荷载作用下标准侧桥塔弯矩包络图

图12 汽车荷载作用下变宽侧桥塔弯矩包络图

4 结语

非对称变宽度斜拉桥结构在其力学性能上存在一定的非对称性。这种非对称性可以从两方面进行考虑：一方面为永久荷载作用下，即结构初始成桥受力状态；另一方面为使用荷载作用下结构的力学响应。以下为主要分析结论。

（1）非对称变宽度斜拉桥的结构恒载是造成内力及位移非对称变化的主要原因。在初始成桥状态下，由于非对称变宽度斜拉桥结构的非对称性会对结构产生较大的影响，为满足主梁的受力要求，斜拉桥的索力可以采用非对称的形式，即在变宽度一侧索力可以适当提高，以满足变宽侧主梁的受力要求。非对称的索力布置对斜拉桥桥塔受力不利，尤其是变宽度一侧的桥塔，由于中跨与变宽边跨的索力并不相等，不平衡的索力要靠桥塔承受，因此桥塔上会产生较大的弯矩。非对称变宽度斜拉桥的合理成桥状态，相比于对称形式的斜拉桥较难达到，由于结构的非对称性，要使主梁和索塔同时达到一个较为合理的状态，必须综合优化考虑主要承重构件的性能及受力。

（2）在使用荷载作用下，变宽侧主梁相对于标准侧增加的弯矩值并不明显，结构的内力及位移分布接近对称的形式，因此，对于非对称变宽度斜拉桥，在使用荷载作用下的结构受力可以忽略非对称性造成的影响。

（3）非对称变宽度斜拉桥的索力优化是控制结构受力达到理想状态的关键问题，合理确定施工期的理想安装索力及控制理想成桥状态索力，是保证非对称变宽度斜拉桥施工期的结构安全及成桥状态合理受力的关键因素。

[1]顾安邦,向中富.桥梁工程(下册)[M].北京:人民交通出版社,2011.

[2]陈开利.日本多多罗大桥景观设计[J].世界桥梁,2002(3):1-4.

[3]A.J.Reis,J.O.Pedro,楼庄鸿.不对称和弯斜拉桥[J].预应力技术,2004(2):30-34.

[4]周杨.单索面高低塔不对称斜拉桥悬臂施工平衡控制[J].公路交通技术,2010,(6):79-81.

[5]Reusink,Jaco,Kuijpers,etal.Designing the Erasmus Bridge,Rotterdam[J].Structural Engineering International.1998(4):275-277.

[6]刘辉锁,刘红卫.变宽度桥梁的设计和技术特点[J].公路,2002,(11):57-59.

[7]李华强.郑州中心区铁路跨线桥基坑支护创新设计与施工[J].公路,2013(8):92-95.

[8]安邦.叠合梁斜拉桥成桥状态及其实现方法的研究[D].大连：大连理工大学,2005.

[9]武利军.基于Midas的斜拉桥索力优化方法与工程实例[J].公路与汽运,2012(5):163-166.

[10]Lee T.Y.,Kim Y.H.,Kang S.W.Optimization of tensioning strategy for asymmetric cable-stayed bridge and its effect on construction process[J].Structural and Multidisciplinary Optimization,2008(35):623–629.