前板桩高桩承台结构工程设计相关问题研究

2014-09-27陈建勇

城市道桥与防洪 2014年8期

陈建勇

（上海市政工程设计研究总院（集团）有限公司，上海市 200092）

0 前言

高桩承台结构是上海地区常见的水工护岸结构型式，能适应上海地区软土地基条件。高桩承台结构的前排桩为板桩墙，后一排或两排桩为方桩（或钻孔灌注桩、PHC管桩），其具有施工方便、占地少等优点，在黄浦江及其支流沿岸和大芦线、苏州河等内河沿岸的护岸工程中被广泛采用。但由于这种结构受力复杂，因此无论是在理论还是实际设计中均存在一些尚未解决的问题，本文针对一些设计过程中遇到的问题进行探讨。

1 问题1：水、土压力计算方法及水位组合

1.1 水、土压力计算方法

高桩承台常作为护岸结构被采用，其承受的荷载主要包括水平向的土压力和水压力，墙后地面均载也是通过水、土体以侧压力的形式作用于墙背结构上，因此水、土压力的正确取值是计算准确的前提，而正确的计算结果则是高桩承台结构安全性及投资合理性相协调的重要前提。

墙后水、土压力计算方法主要有水土分算和水土合算两种方法。水土合算以土粒与孔隙水共同组成的土体作为对象，直接用土的饱和重度计算侧压力。这一原则对于不透水的粘土层较为适用，但在理论上存在缺陷[1]，且对于计算中土体强度指标的取值争论较多，而在大量工程实践的基础上，根据统计分析直接给出某一地区水土合算的侧压力计算公式已成为可能。根据《上海市基坑工程设计规程》，上海地区水土压力的总的侧压力系数在0.55～0.75的范围内选取[2]。水土分算则分别计算土压力和水压力，两者之和即为总侧压力，适用于土体孔隙中存在自由的重力水的情况，或土的渗透性较好的情况，一般适用于砂土、粉土和粉质粘土。由于在实际工程中，为了减少墙后侧向土压力，往往回填渗透性高的砂土或碎石土，且由于水土分算结果往往较合算大，而前板桩高桩承台结构对水平荷载较敏感，因此在实际设计中建议采用较保守的水土分算。

1.2 水压力的计算

关于水压力的常用计算方法一般不考虑渗流的影响，即墙后计算水位以上为三角形分布，以下为矩形分布。

根据《上海市基坑工程设计规程》中关于水土分算中水压力的计算，应按有无产生地下水渗流情况，采用不同的分布模式[2]。当地下水无渗流时，墙后静水位以上静水压力按三角形分布计算，静水位以下按矩形分布计算；当考虑地下水渗流时，又根据是否考虑挡墙的隔水作用墙后水压力分别按倒梯形和倒三角分布计算，各分布型式如图1所示。可见是否考虑地下水渗流对水压力的计算结果影响较大，因此在设计时需要根据实际的地下水情况采取不同的分布模式，鉴于倒梯形与倒三角形分布水压力总和相近，且后者计算更方便，因此在考虑地下水渗流时本文建议近似根据倒三角形分布计算水压力。（注：此处为完整表达，引用1997年版《上海市基坑工程设计规程》，2010年新版《上海市基坑工程技术规范》已调整了土、水压力计算方法，不再采用合算方法，考虑地下水渗流作用时地下水位以下水压力分布只保留直接按照渗流路径由直线比例确定水压力分布[3]的方法，在扣除墙前部分水压力后实则上即是1997年版中的倒三角形分布模式。）

1.3 土压力的计算

前板桩高桩承台结构目前仍较多采用竖向弹性地基梁的方法计算。根据弹性地基梁的土压力计算模式，墙前、后均采用静止土压力，考虑到结构受水平荷载后有向前的位移，因此采用主动土压力代替静止土压力。常用的土压力计算图如图2所示。

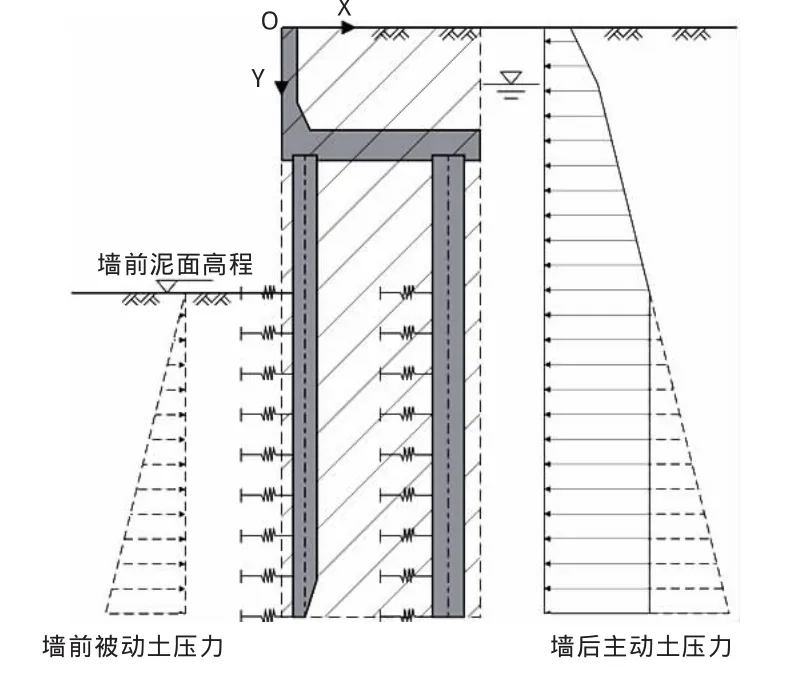
图2 土压力计算图

在实际工程中，前板桩高桩承台结构墙前基本为后开挖的情况。因此需要考虑墙前土的超固结效应，有学者提出了超固结比对静止土压力系数影响的关系式[4]：

式中：Ko（OC）——超固结状态的静止土压力系数；

Ko（NC）——正常固结状态静止土压力系数；

A、B、α、m——试验数据得到的常数值，见表1所列。

表1 试验得到的超固结效应下静止土压力影响系数值一览表

上述公式表明，静止土压力系数由于超固结比（OCR）的增加而发生的变化，即当超固结比OCR=1～2.5时呈线性关系，OCR<2.5时呈非线性关系。

也有学者提出了残余应力的概念，给出了残余应力影响深度的计算公式，并通过对上海地区工程实录的数据整理分析发现如下经验关系：

式中：H——基坑开挖深度，m；

hr——残余应力影响深度，m。

由于前板桩高桩承台结构前沿开挖范围一般为长条形，相比基坑工程，开挖的范围对墙前土体应力也具有一定影响。本文提出可将开挖土体部分当作施加在设计泥面的一个负的均布荷载，根据土力学中条形基底竖直均布荷载作用时土体中产生附加应力的结论，当应力计算点深度与均布荷载宽度比为1.5时，水平向的地基应力附加系数可忽略不计。为了便于计算，本文推荐采用残余应力的概念，并选取上式的计算结果与1.5倍的开挖宽度这两者间的小值，作为应力的影响深度。对结构土压力进行修正后如图3所示。

1.4 墙前、墙后水位组合问题

在高桩承台结构设计中，经常采用墙前低水位或无水而墙后为高地下水位时的组合情况，因为这是墙前、后水位差最大，对结构稳定最不利。但由于前板桩高桩承台结构抵抗水平荷载的能力较差，最后往往因为计算得到的剩余水压力较大而造成不必要的浪费。

图3 墙前被动土压力经残余应力修正后的土压力计算图

《水工挡土墙设计规范》中提出，考虑到墙后土中渗流及其滞后性，对于潮汐河道上的挡土墙，其墙前、墙后水位差取相应最不利条件下最大潮差值的1/3～1/2为宜；对于水库或退水迅速的行洪河道上的挡土墙，取相应最不利条件下最大水位差值的1/2为宜；对于无潮汐影响河道的挡土墙，考虑降雨及渗流滞后的影响，在正常运行工况下挡土墙墙前、墙后的水位差可取0.5～1.0 m[5]。因此在设计中，应合理地选择水位组合工况，避免为了提高结构安全性而一味地增加荷载，鉴于该种结构剩余水压力合力作用点距泥面越远时对结构稳定越不利，因此墙后可取较高的地下水位，墙前水位根据规范推荐采用的水头差选取。

2 问题2：关于桩与承台连接问题

2.1 桩顶连接计算方式

高桩承台结构其底板（即承台）厚度一般较薄，而且桩较密，为方便承台底面钢筋配扎，桩与承台的连接通常采用桩顶嵌入承台50～100 mm，桩顶主筋锚入长度不小于35 d的方式。由于桩与承台自身刚度相近，设计中一般均假定桩顶为固结，计算结果往往是桩顶弯矩最大，而前排桩桩轴力远大于后排桩，继而根据这两个值来确定桩型及前排桩长。

但实际情况由于桩顶伸入承台较浅，当桩顶弯矩较大时，桩周混凝土会出现一定开裂，使得桩与承台相对位移变大，形成塑形饺而释放弯矩，桩身弯矩最大值将出现在桩中部，而且后排桩所受的桩轴力及结构水平位移也将大于按固结计算的结果。因此，只根据桩顶固结的方式设计缺乏足够的安全度。根据朱海堂等的实验结论[6]，桩顶伸入承台较短且桩强度较大时，将发生节点连接破坏型式，节点破坏时桩顶所受的弯矩和剪力可以用下式计算：

本文建议设计时可先按桩顶固结进行计算，根据计算结果验算水平位移、配置桩顶及底板钢筋，第二步再按照桩顶铰接计算，核算桩身弯矩及后排桩桩轴力。

2.2 算例

本文选用实际项目作为算例，分别通过以下方法进行计算：

（1）常用计算方法（即未考虑渗流对水压力的影响、未考虑墙前开挖土体的残余应力、采用桩与承台固结）；

（2）本文推荐计算方法（考虑上述水、土压力条件，采用桩顶与承台固结计算、铰接复核）。

对计算结果进行比较分析，算例结构简图见图4所示，其基本参数见表2～表4所列。

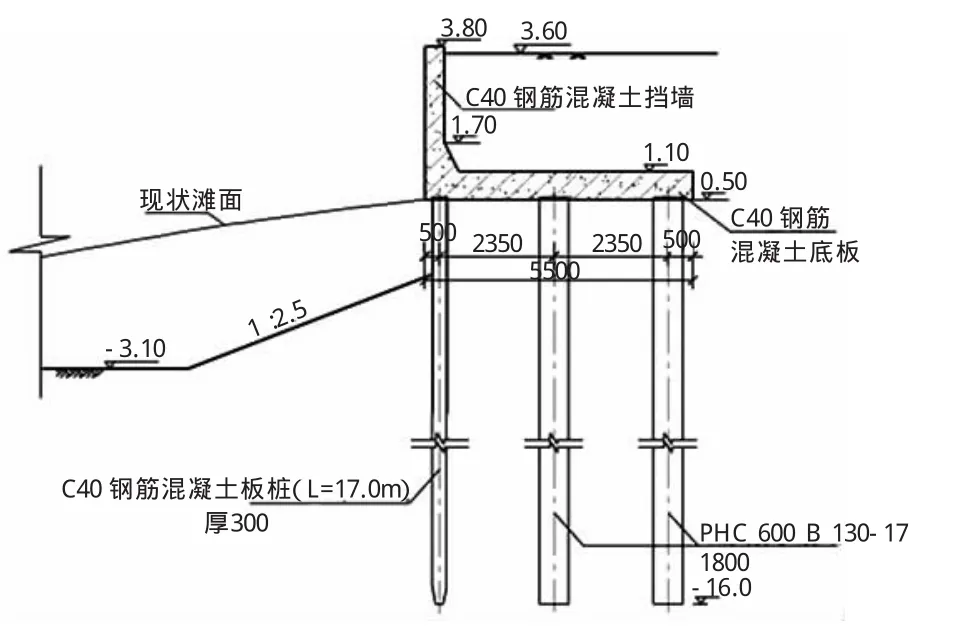
图4 高桩承台结构计算简图

表2 某工程高桩承台结构设计参数表（一）

表3 某工程高桩承台结构设计参数表（二）

表4 算例采用的地质力学参数表

常用计算方法（桩顶固结）计算结果见图5～图8所示，表5所列。

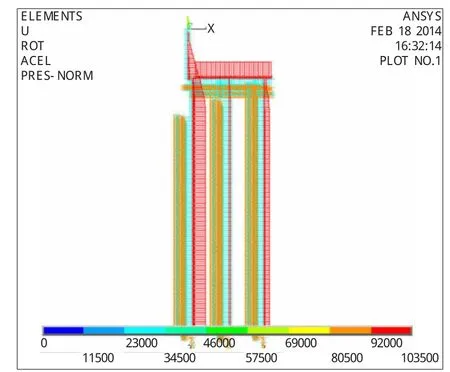
图5 常用计算方法（桩顶固结）结构计算模型

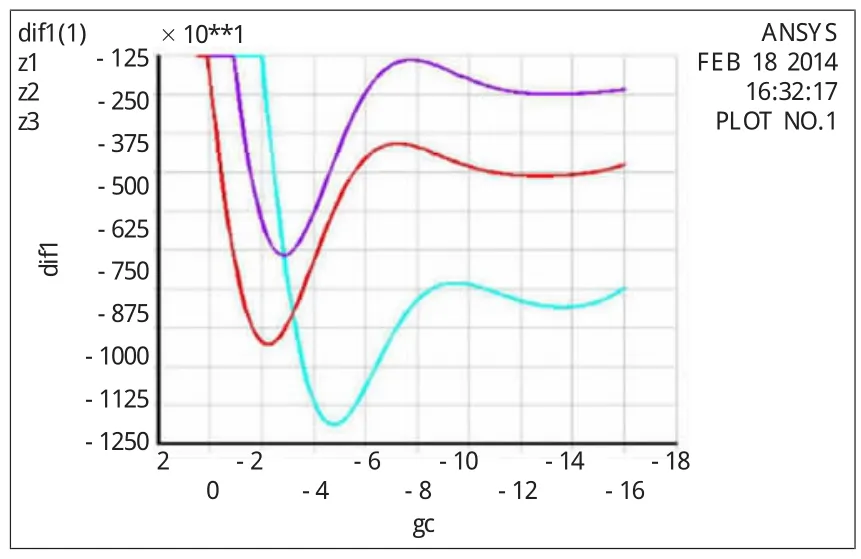
图6 常用计算方法（桩顶固结）桩前地基反力图

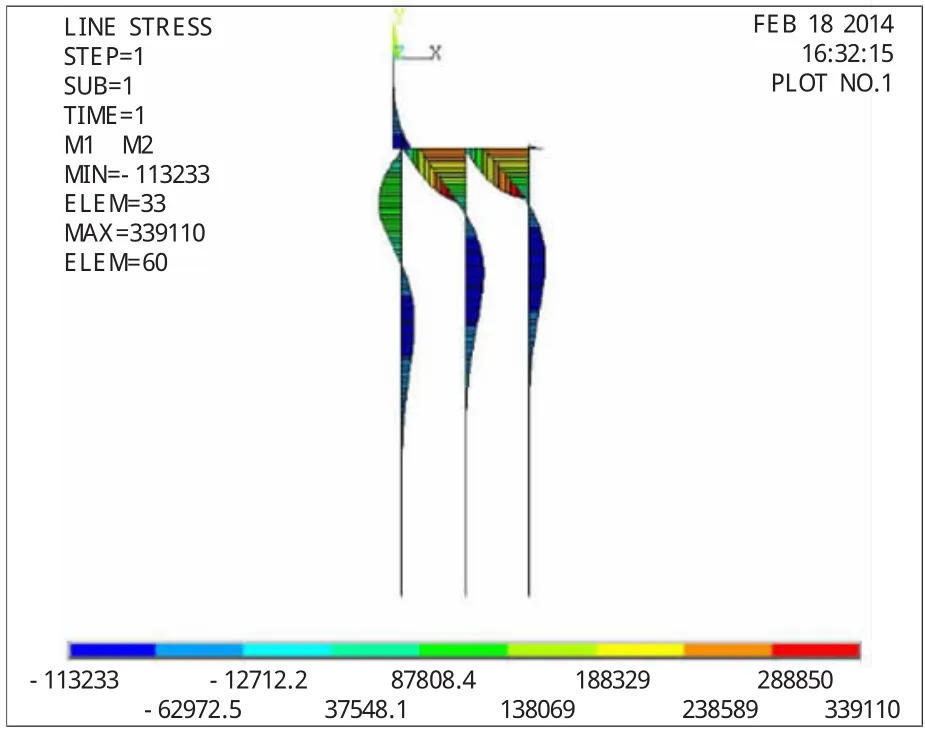
图7 常用计算方法（桩顶固结）结构弯矩图

图8 常用计算方法（桩顶固结）结构轴力图

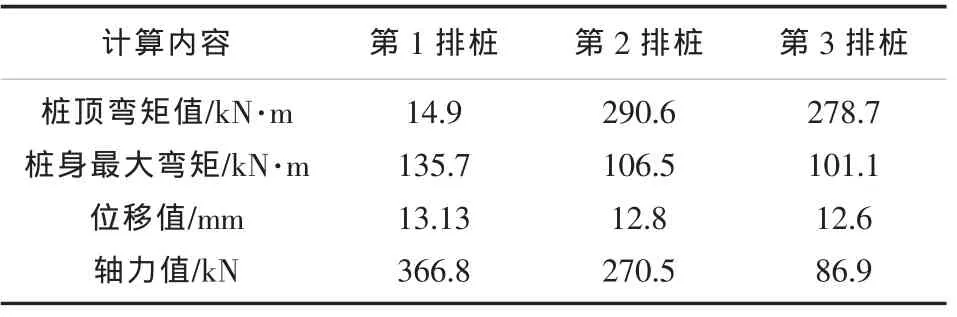
表5 常用计算方法（桩顶固结）结果汇总表（标准值）

本文推荐计算方法（桩顶固结）的计算结果见图9～图12所示，表6所列。

图9 推荐计算方法（桩顶固结）结构计算模型

图10 推荐计算方法（桩顶固结）桩前地基反力图

图11 推荐计算方法（桩顶固结）结构弯矩图

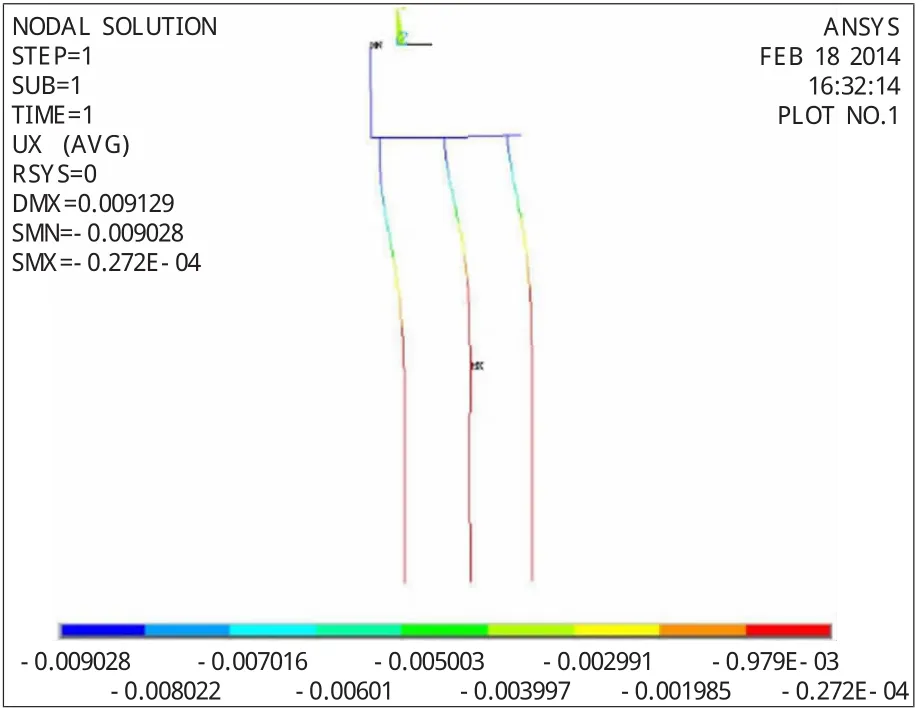
图12 推荐计算方法（桩顶固结）结构轴力图

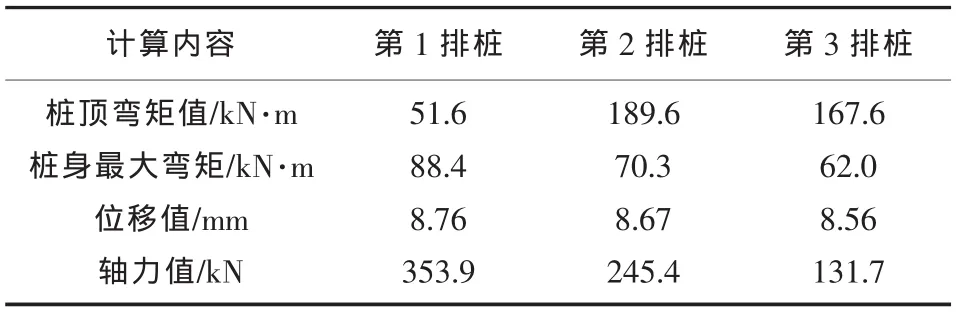
表6 推荐计算方法（桩顶固结）结果汇总表（标准值）

采取桩顶铰接计算方法核算桩身弯矩结果见图13～图15所示。表7为高桩顶台结构穹矩计算汇总表（标准值）。

图13 推荐计算方法（桩顶铰接）桩前地基反力图

图14 推荐计算方法（桩顶铰接）结构弯矩图

图15 推荐计算方法（桩顶铰接）结构轴力图

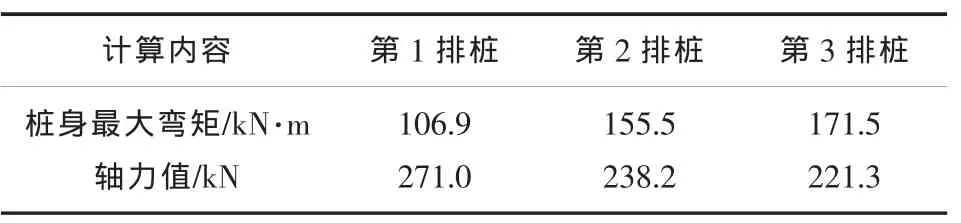
表7 高桩承台结构弯矩计算汇总表（标准值）

采用常用的计算方法与本文推荐的计算方法在计算结果上的比较如表8所列。

表8 常用方法与本文推荐方法计算结果对比一览表

从表8可知，采用常用方法计算所得的桩顶位移及后排桩顶弯矩均较本文计算结果大，且为本文计算值的1.5倍以上；而后两排桩的桩身最大弯矩计算值较本文计算方法小约50%以上；特别是第三排桩桩轴力仅为本文计算值的1/3。可见对于桩顶弯矩常用计算方法安全富裕度过大，而桩身弯矩又偏于危险，特别是第三排桩轴力。

如果采用常用计算方法的结果，在桩顶弯矩满足条件的基础上，设计人员往往会加大第二（两排桩情况时）、三排桩间距。虽然在一般情况下是比较合理，但若墙后超载或墙前超挖严重，桩顶出现塑性铰的情况下，后排桩的桩轴力将明显增大，若桩基承载力不足，则会造成承台向后倾斜，使得承台底板弯矩迅速增大，底板有断裂危险，导致严重的出险后果。