多机系统发电机组强励电压倍数优化配置算法

周 云 ，严 正 ，李乃湖 ，2，曹 路

（1.上海交通大学 电力传输与功率变换控制教育部重点实验室，上海 200240；2.阿尔斯通电网中国技术中心，上海 201114；3.华东电网有限公司，上海200120）

0 引言

励磁系统是发电机组的重要组成的部分，性能良好的励磁系统可以提高发电机的可靠性和稳定性［1］。随着电力二极管和晶闸管技术的日益成熟，电厂越来越趋向于选用无刷励磁系统和静止励磁系统［2］。励磁系统强励电压倍数或称顶值电压倍数（以下简称强励倍数），是励磁顶值电压与额定励磁电压之比，是励磁系统主要的大干扰性能指标［3］。静止励磁系统是指励磁电源从发电机机端取得的励磁控制系统，响应速度快，但强励能力易受机端电压影响［4］。和静止励磁系统相比，无刷励磁系统利用同轴旋转的交流励磁机作为励磁电源，全部励磁功率取自轴系，强励能力不受机端电压的影响。

文献［5-6］分析了发电机励磁系统强励功能和作用，发电机组的强励能力可以在故障后向系统注入动态无功功率，提高机组的强励倍数可以提高系统的暂态稳定性。文献［7］研究了静止励磁方式励磁系统模型参数对系统暂态稳定性的影响。文献［8］研究了强励对交直流混合输电系统暂态稳定裕度的影响。文献［9］利用扩展等面积法则，提出了基于广域测量系统的发电机强励控制方案。

单机无穷大等效是一种混合的时域直接方法［10］，文献［11］研究了系统在2种等值方式下的暂态稳定裕度，为单机无穷大母线OMIB（One Machine Infinite Bus）等值模型的暂态稳定分析和控制提供了研究基础。文献［12-13］利用OMIB等值模型在暂态稳定约束最优潮流模型中引入严格的暂态稳定判据。文献［14］利用OMIB模型研究了计及暂态稳定约束的电厂送出系统重合闸时间整定方法。

本文通过建立多机系统的 OMIB 模型［10，15］，定量计算出多机系统在预设故障下的暂态稳定裕量；建立并比较了无刷和静止这2种主要励磁方式下强励倍数对系统暂态稳定的影响模型；基于强励倍数对暂态稳定的影响模型提出了多机系统机组强励倍数优化配置算法；利用IEEE 3机9节点系统和新英格兰系统的算例验证了算法的有效性和准确性。

1 多机系统的OMIB模型

1.1 多机系统的OMIB等值

对多机系统进行短时间时域仿真，仿真过程中对机组功角排序，最大功角间隔达到某一数值（如360°）时，分别定义功角相对超前和滞后的发电机群为临界机群C和常规机群N，相应地建立系统的OMIB等效模型，具体的等值公式见文献［16］。通过对OMIB等效模型的分析计算，克服了传统时域方法缺少灵敏度和控制信息的缺点［17］，可以定量计算出比较精确的系统暂态稳定裕量以表征系统的暂态稳定性。

1.2 OMIB轨迹分类

根据等值，可以将OMIB轨迹分为暂态不稳定、稳定和极限稳定（不稳定）3种情况，应注意的是本节仅叙述单摆稳定的情况。

不稳定OMIB轨迹如图1所示，图中，PE为等效系统电磁功率；PM为等效系统机械功率；δ0和δcl分别为预设故障发生时刻t0和故障清除时刻tcl对应的系统等效功角值；Adec、Aacc分别为减速面积和加速面积。式（1）为不稳定轨迹的判断条件。其中，Pa和ω分别为等效后的系统加速功率和角速度；tu为系统不稳定时刻，δu为tu时刻对应的不稳定功角值。

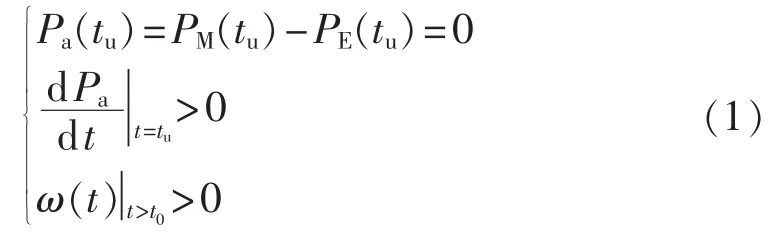
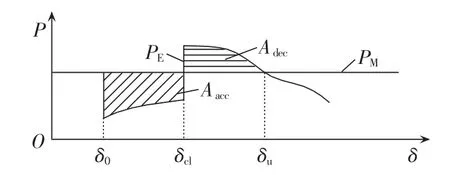
图1 不稳定OMIB轨迹Fig.1 Unstable OMIB trajectory

稳定OMIB轨迹如图2所示。

图2 稳定OMIB轨迹Fig.2 Stable OMIB trajectory

式（2）为稳定轨迹的判断条件，其中，tr为返回时刻，δr为tr对应的返回功角值。当返回功角δr和不稳定功角δu相等时则为极限稳定（不稳定）情况。

1.3 OMIB模型暂态稳定裕量计算

OMIB的动态模型由式（3）给出，是等效模型的运动方程；系统的暂态稳定裕量η见式（4）。

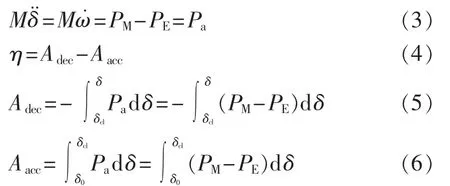
其中，M为系统等效惯性系数。

a.不稳定OMIB轨迹暂态稳定裕量。

将 δ=δu代入式（3）并与式（4）比较，可得不稳定OMIB轨迹的暂态稳定裕量计算公式如下：

b.稳定OMIB轨迹暂态稳定裕量。

将 δ=δr代入式（3），且因 ω（tr）=0，稳定 OMIB轨迹的暂态稳定裕量计算公式如下：

2 强励倍数对系统暂态稳定影响模型

2.1 无刷励磁方式下的线性关系影响模型

表1和表2是IEEE 3机9节点系统［18］（以下简称系统 1）和新英格兰系统［19］（以下简称系统 2）考虑的预设故障集（故障线路列中的数字为节点编号），机组采用无刷励磁方式，励磁模型采用FF卡模型①印永华，卜广全.PSD-BPA暂态稳定程序用户手册.2005.。对机组励磁系统配置不同的强励倍数，建立系统OMIB模型，计算系统在预设故障下的暂态稳定裕量。时域仿真工具采用PSD-BPA 4.14，分析环境为MATLAB 2011b。参照国家标准GB/T 7409.3—2007《同步电机励磁系统大、中型同步发电机组励磁系统技术要求》［20］，本节机组强励倍数i的设置范围为［1.0，2.0］。图3为对系统1机组分别配置不同的强励倍数时，故障A下系统暂态稳定裕量及其和强励倍数的关系拟合曲线，详细计算结果见表3。机组采用无刷励磁方式时，故障B下系统暂态稳定裕量及其和强励倍数的关系拟合曲线见图4。

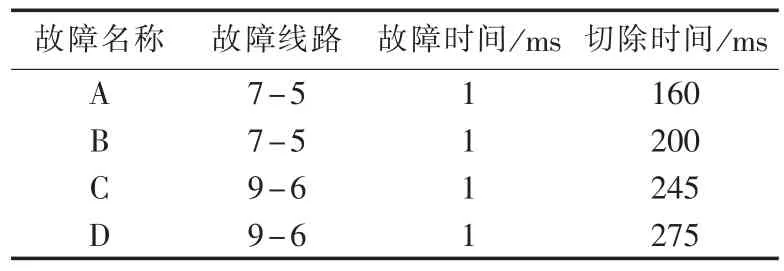
表1 IEEE 3机9节点系统预设故障集Table 1 Preset fault set of IEEE 3-machine 9-bus system

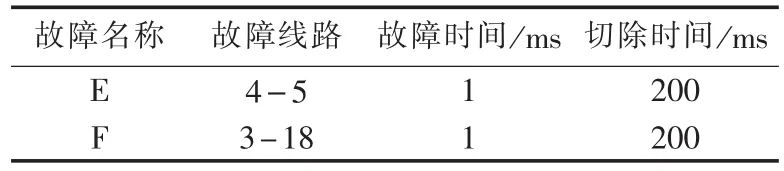
表2 新英格兰系统预设故障集Table 2 Preset fault set of New England system

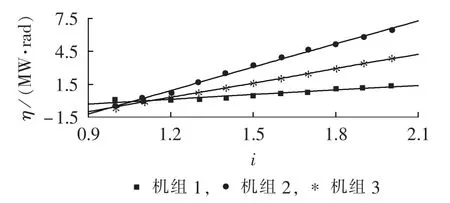
图3 无刷励磁方式下，系统1发生故障A时的系统稳定裕量和强励倍数的关系Fig.3 Relationship between stability margin and FEVR when fault A occurs in system 1 under brushless excitation mode

参照图3，对系统暂态稳定裕量进行线性拟合。表4和表5分别为考虑不同预设故障时，系统1、2的线性拟合相关系数值。根据拟合相关系数值可知，采用无刷励磁方式时，预设故障下的系统暂态稳定裕量和机组强励倍数之间存在线性关系。

2.2 静止励磁方式下的二次多项式关系影响模型

机组采用静止励磁方式时，模型采用FD卡模型①印永华，卜广全.PSD-BPA暂态稳定程序用户手册.2005.，其他设置同无刷励磁方式。图5为配置不同的强励倍数时，系统1机组发生故障B时系统暂态稳定裕量及其和强励倍数的拟合曲线图，详细计算结果见表6。机组采用静止励磁方式时，系统1发生故障A时的系统暂态稳定裕量及其和强励倍数的拟合曲线见图6。

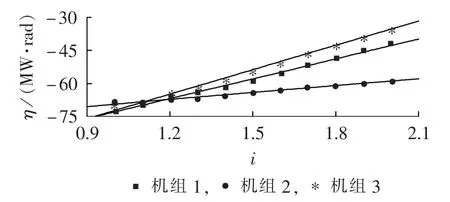
图4 无刷励磁方式下，系统1发生故障B时的系统稳定裕量和强励倍数的关系Fig.4 Relationship between stability margin and FEVR when fault B occurs in system 1 under brushless excitation mode

表4 不同预设故障下，系统1各机组的线性拟合相关系数Table 4 Unit linear fitting correlation coefficient of system 1 for different preset faults

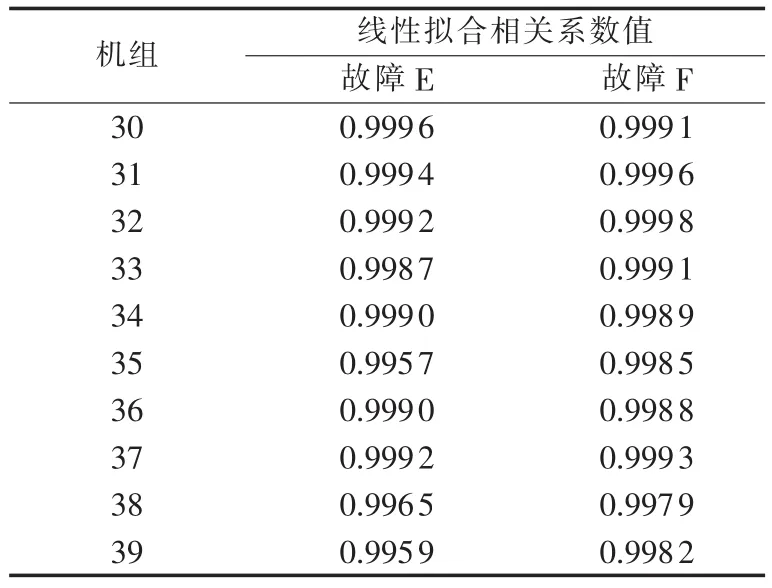
表5 不同预设故障下，系统2各机组的线性拟合相关系数Table 5 Unit linear fitting correlation coefficient of system 2 for different preset faults

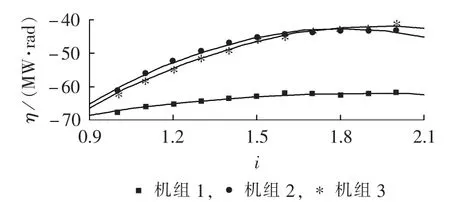
图5 静止励磁方式下，系统1发生故障B时的系统稳定裕量和强励倍数的关系Fig.5 Relationship between stability margin and FEVR when fault B occurs in system 1 under static excitation mode

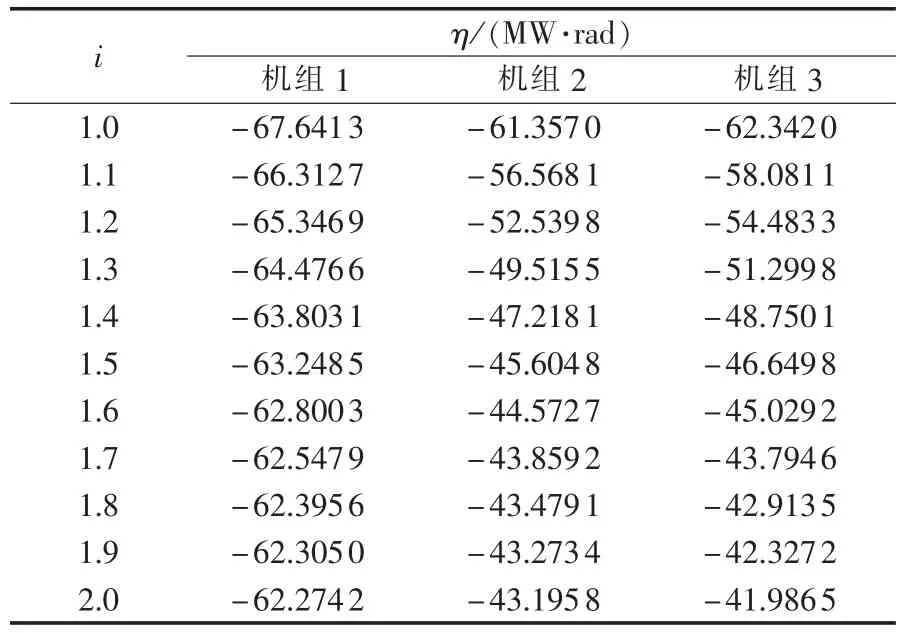
表6 采用静止励磁方式后，发生故障B时，系统1各机组在不同的强励倍数下的暂态稳定裕量Table 6 Transient stability margin of units for different FEVRs when fault B occurs in system 1 under static excitation mode

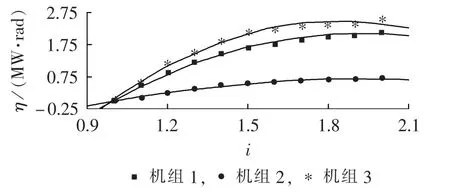
图6 静止励磁方式下，系统1发生故障A时的系统稳定裕量和强励倍数的关系Fig.6 Relationship between stability margin and FEVR when fault A occurs in system 1 under static excitation mode

参照图5，对系统暂态稳定裕量进行二次多项式拟合。表7和表8分别为考虑不同预设故障时，系统1、2的二次多项式拟合相关系数值。根据拟合相关系数值可知，当机组采用静止励磁方式时，系统暂态稳定裕量与机组强励倍数存在二次多项式关系。

2.3 无刷励磁和静止励磁方式比较

图7和图8分别为采用无刷和静止励磁方式时，系统1发生故障A时机组3和系统2发生故障E时机组30的系统暂态稳定裕量及其与机组强励倍数的关系拟合曲线。表9为图7、8中曲线的拟合结果，其中无刷励磁方式下采用线性拟合，静止励磁方式下采用二次多项式拟合。

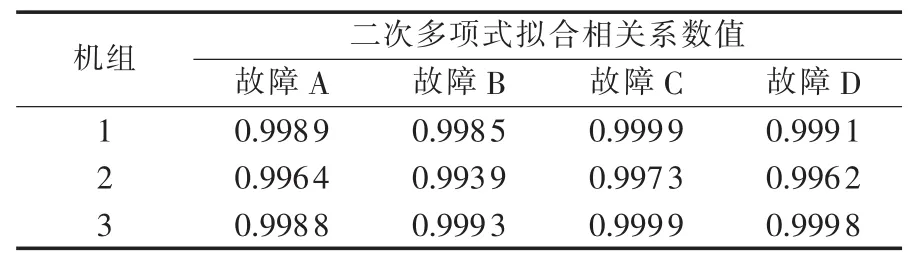
表7 不同预设故障下，系统1各机组的多项式拟合相关系数Table 7 Unit poliminal fitting correlation coefficient of system 1 for different preset faults

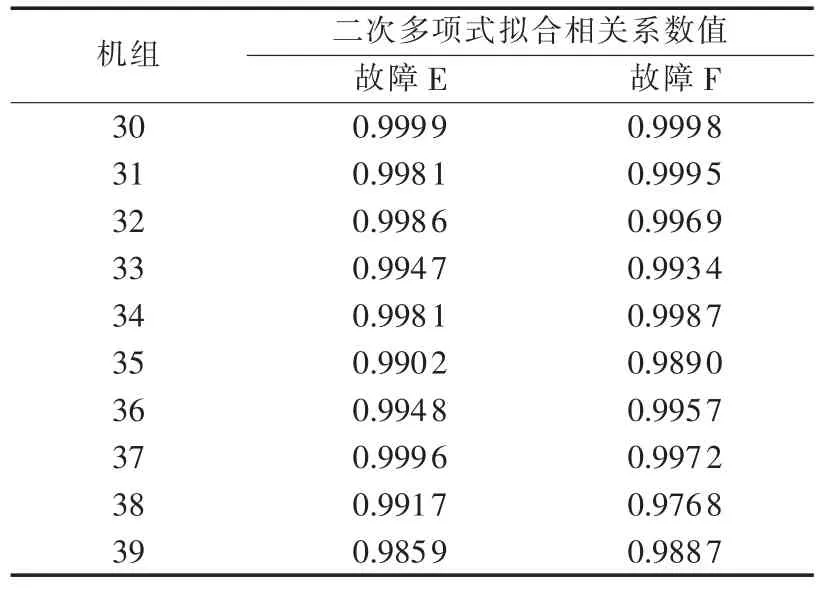
表8 不同预设故障下，系统2各机组的多项式拟合相关系数Table 8 Unit poliminal fitting correlation coefficient of system 2 for different preset faults

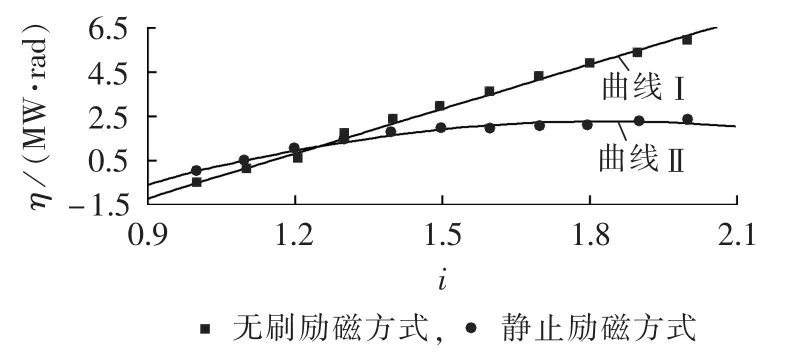
图7 系统1发生故障A时，其机组3在无刷励磁和静止励磁方式下的稳定裕量和强励倍数的关系Fig.7 Relationship between stability margin and FEVR of unit 3 when fault A occurs in system 1 for brushless and static excitation modes

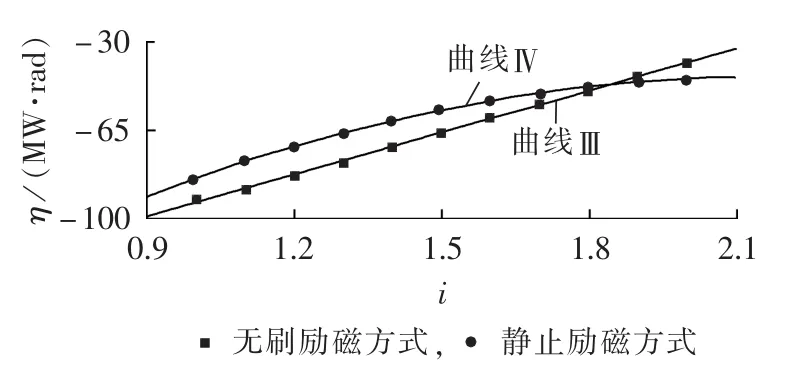
图8 系统2发生故障E时，其机组30在无刷励磁和静止励磁方式下的稳定裕量和强励倍数的关系Fig.8 Relationship between stability margin and FEVR of unit 30 when fault E occurs in system 2 for brushless and static excitation modes

图9为采用静止励磁方式时系统2发生故障F时机组38的暂态稳定裕量-强励倍数曲线。当强励倍数在［1.0，1.6］内时暂态稳定裕量随着强励倍数的增加而增加；强励倍数大于1.6之后，产生饱和现象，暂态稳定裕量不再增加，系统的暂态稳定性不再随强励倍数的提高而改善。达到饱和现象之前，静止励磁方式下的二次多项式关系影响模型依然适用。

表9 稳定裕量和强励倍数的关系拟合结果Table 9 Fitting results of relationship between stability margin and FEVR

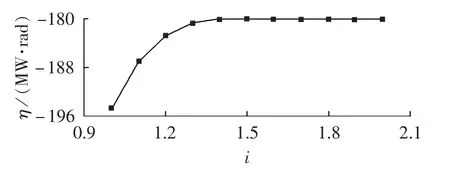
图9 系统2发生故障F时，其机组38在无刷励磁和静止励磁方式下的稳定裕量和强励倍数的关系Fig.9 Relationship between stability margin and FEVR of unit 38 when fault F occurs in system 2 for brushless and static excitation modes

静止励磁系统饱和现象产生的原因为励磁系统强励能力的饱和。系统故障后，机端电压发生下降，励磁系统强励能力使得机组向系统注入更多的无功功率，维持系统的电压，提高系统的暂态稳定性。无刷励磁方式由于全部励磁功率取自轴系，提高强励倍数即提高励磁顶值电压之后，充足的励磁功率来源保证了励磁系统的强励能力。静止励磁方式励磁功率取自机端，故障严重情况下，机端电压严重下降，即使提高励磁顶值电压，励磁功率的缺失也会使得励磁系统输出的励磁电压不能达到设定的励磁顶值电压，造成强励能力的饱和。

结合计算结果和拟合曲线，静止励磁方式下增加强励倍数改善系统暂态稳定性的能力的方式受到系统故障的影响。对比无刷励磁方式对暂态稳定的线性影响模型和静止励磁方式的二次多项式影响模型可知，一定强励倍数范围内，机组采用无刷励磁方式有利于持续提高系统的暂态稳定性。

3 多机系统机组强励倍数优化配置

尽管相比于静止励磁方式的二次多项式影响模型，一定强励倍数范围内采用无刷励磁，通过增加机组的强励倍数，系统的暂态稳定性可以得到持续提高，但由于无刷励磁对励磁机、旋转二极管等方面的要求，对相同规模机组，无刷励磁系统成本一般大于静止励磁系统［21］。提高励磁系统强励倍数意味着励磁系统成本的增加。励磁系统的总投资一定时，可通过机组强励倍数的优化配置，增加系统暂态稳定裕量，提高系统的暂态稳定性。

3.1 优化配置模型

3.1.1 考虑强励倍数励磁系统成本模型

文献［20］中规定励磁系统最低强励倍数为1.6，优化配置模型中励磁系统额定强励倍数不妨设为1.6。不考虑市场因素，励磁系统的额定成本近似和机组额定容量成正比。式（9）为机组励磁系统额定成本CN的计算公式。

其中，C0为成本系数；PN为机组额定容量。

目前部分实际机组励磁系统强励倍数可以超过2.0［8］，优化配置模型中励磁系统强励倍数设置区间设为I1=［1.0，2.5］。因为强励倍数额定值为1.6，强励倍数可调节区间设为I2=［1.6，2.5］。假设励磁系统成本和强励倍数之间存在线性关系，则式（10）是强励倍数为i时励磁系统成本C（i）的计算公式。

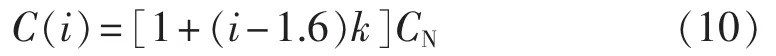
其中，k为递增常数。

3.1.2 暂态稳定影响模型

根据无刷励磁方式下系统暂态稳定裕量与强励倍数存在的线性关系，以及静止励磁方式下两者之间存在的二次多项式关系，结合图3和图5，建立系统OMIB模型计算强励倍数值对应的暂态稳定裕量，通过线性和二次多项式拟合得到暂态稳定裕量-强励倍数曲线。因为静止励磁方式存在饱和现象，一般取较小的强励倍数值进行计算拟合以减小饱和现象造成的影响，待拟合数据点对应的强励倍数选取区间取 I3=［1，1.3］。

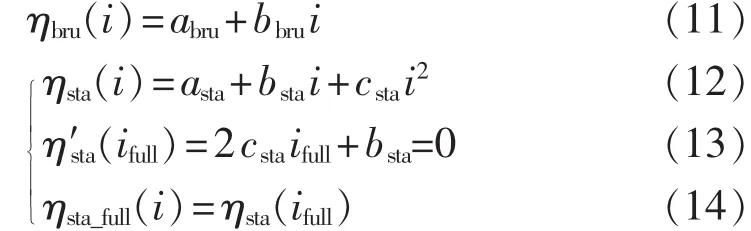
式（11）为无刷励磁方式下系统暂态稳定裕量-强励倍数拟合曲线函数，区间I3内取3个强励倍数值，计算系统在不同强励倍数下的暂态稳定裕量，系数 abru和bbru通过对3组数据的线性拟合得到。式（12）为静止励磁方式下系统暂态稳定裕量-强励倍数的拟合曲线函数，区间I3内取4个强励倍数计算得到待拟合数据，系数asta、bsta、csta通过对这些数据进行二次多项式拟合得到。满足式（13）的ifull为静止励磁方式下的饱和强励倍数，若ifullϵI1则存在饱和现象。对 iϵI1且 i≥ifull，则通过式（14）计算对应的暂态稳定裕量。

3.1.3 暂态稳定边际成本

式（15）为机组暂态稳定边际成本L的计算公式。当机组采用无刷励磁方式时 η（i）=ηbru（i），采用静止励磁方式时 η（i）=ηsta（i）。

边际成本L（i）的含义是机组在强励倍数下，系统增加单位暂态稳定裕量对应的励磁系统的增加成本。若有多台机组强励倍数在可调节区间I2内，优先增加暂态稳定边际成本最小机组的强励倍数。

3.2 强励倍数优化配置算法

考虑励磁系统总投资一定，机组励磁方式确定，系统可能发生的主要故障为预设故障。通过机组强励倍数优化配置，使系统在预设故障下暂态稳定性最佳。图10为优化配置算法流程，其中，G为机组集合；ip为机组 p 强励倍数；Cp（ip）为机组 p 励磁成本函数；ηp（ip）为机组 p暂态稳定裕量-强励倍数拟合曲线函数；Lp（ip）为机组p暂态稳定边际成本；Csum为励磁系统总投资；Δi为强励倍数递增常数。

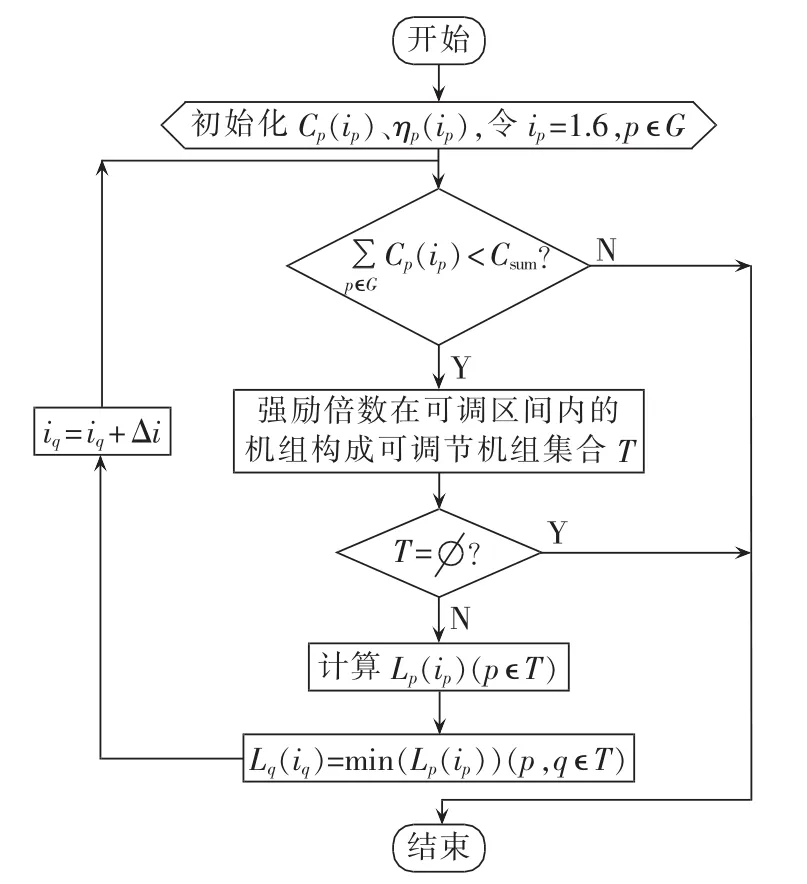
图10 所提算法的流程Fig.10 Flowchart of proposed algorithm

根据系统参数构造机组考虑强励倍数的励磁成本Cp（ip），确定系统考虑的主要预设故障。根据机组不同励磁方式，在I3内选取强励倍数值，计算系统暂态稳定裕量，通过拟合得到机组暂态稳定裕量-强励倍数拟合曲线函数。

强励倍数在可调节区间内的机组构成可调节机组集合T，计算T内所有机组的暂态稳定边际成本Lp（ip），递增边际成本最小的机组的励磁系统强励倍数。若此时励磁系统总成本小于总投资Csum且T非空，则重复暂态稳定边际成本的计算及机组强励倍数的递增，否则结束循环。此时得到的系统各机组强励倍数值即为考虑主要故障下励磁总投资为Csum时多机系统机组强励倍数最优配置结果。

3.3 考虑多故障情况的机组强励倍数优化

考虑到故障点位置及故障形式的不同对暂态稳定裕量及边际成本的影响，式（16）和（17）分别为系统考虑多故障情况的概率暂态稳定裕量ηP和概率暂态稳定边际成本LP（i）的计算公式。

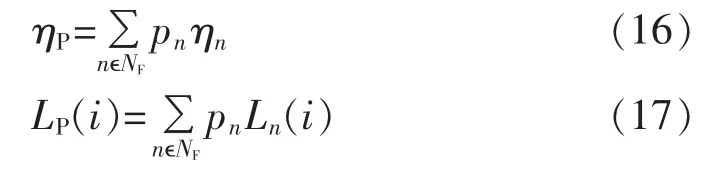
其中，NF为系统考虑的多故障集合；pn为故障n的相对发生概率；ηn为故障n下系统的暂态稳定裕量；Ln（i）为机组在强励倍数i的条件下对应故障n的暂态稳定边际成本，利用故障相对发生概率对不同故障条件下的机组暂态稳定边际成本加权求和，即为概率暂态稳定边际成本。值得注意的是，机组采用静止励磁方式时，考虑到饱和现象的存在，若机组仅对部分故障饱和，则利用式（18）计算机组概率暂态稳定边际成本，其中NF_un为机组的强励倍数i的条件下对应的不饱和故障集合。

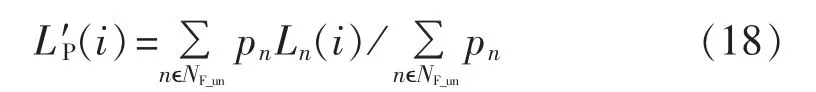
系统考虑多故障情况，以系统概率暂态稳定裕量为优化目标，在强励倍数优化配置算法中，用机组概率暂态稳定边际成本代替系统仅考虑主要故障情况的边际成本，计算流程同单一故障情况。在励磁系统总投资一定的情况下优先增加概率暂态稳定边际成本最小机组的强励倍数，计算得到的强励倍数最优配置结果使得多故障情况下系统概率暂态稳定裕量最大。

4 算例分析

4.1 系统1算例

系统1数据见文献［18］，假设机组均采用无刷励磁方式，额定强励倍数设为1.6，系统考虑的主要故障对应表1中的故障D。强励调节区间设为I2=［1.6，2.5］，拟合数据强励倍数的选取区间设为 I3=［1，1.3］。无刷励磁方式系统成本系数设为C0=1（MV·A）-1，非额定状态下励磁系统成本递增常数设为k=1，励磁系统总投资Csum进行归一化处理后取为1000，强励倍数递增常数设为Δi=0.01。

因为机组均采取无刷励磁方式，所以在I3内选取1.0、1.1和1.2这3个强励倍数值，计算系统在不同机组相应强励倍数下的暂态稳定裕量，计算结果见表10。对表10中的计算结果进行线性拟合得到的机组稳定裕量-强励倍数曲线函数如表11所示。

系统机组强励倍数优化配置算法的计算结果为：机组2和机组3的强励倍数达到可调节区间I2中的最大值2.5，机组1的强励倍数为2.18。表12列出了系统在6种机组强励倍数不同配置下的各机组强励倍数值及系统对应的暂态稳定裕量。图11、12分别为额定配置和最优配置下系统OMIB模型功角特性曲线。机组强励倍数额定配置下系统的OMIB功角特性对应不稳定OMIB轨迹，预设故障下系统暂态失稳。最优配置下系统的OMIB功角特性对应稳定OMIB轨迹，系统保持暂态稳定。

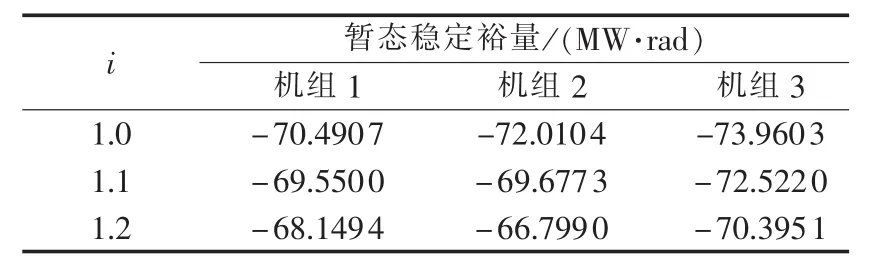
表10 系统1在不同强励倍数下的暂态稳定裕量Table 10 Transient stability margin of system 1 for different FEVRs

表11 系统1各机组的励磁成本函数和暂态稳定裕量拟合函数Table 11 Excitation cost function and transient stability margin fitting function for units of system 1

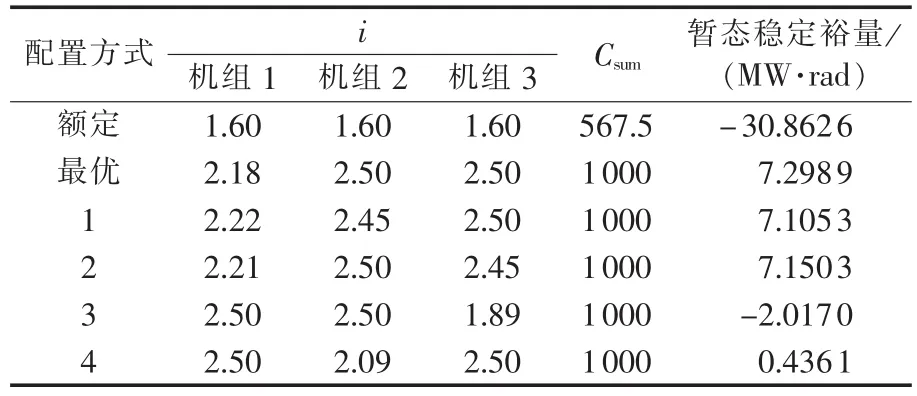
表12 系统1在不同强励倍数配置方案下的暂态稳定裕量结果Table 12 Transient stability margin of system 1 for different FEVR configurations

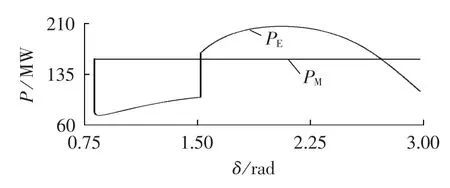
图11 额定配置下OMIB模型的功角特性Fig.11 Power-angle characteristics of OMIB model with nominal FEVR configuration

图12 最优配置下系统OMIB模型的功角特性Fig.12 Power-angle characteristics of OMIB model with optimal FEVR configuration

配置方式1和配置方式2是最优配置方式的2组对比配置，比较最优配置方式、配置方式1和配置方式2下的系统暂态稳定裕量值可知，最优配置方式下系统暂态稳定裕量最大。励磁系统总投资一定时，励磁系统强励倍数最优配置方式下系统在主要预设故障时暂态稳定性最佳。

若计算过程中优先增加暂态稳定边际成本最大机组的强励倍数，机组强励倍数配置结果为表12中的配置方式3，对应的系统暂态稳定裕量为-2.0107 MW·rad，系统暂态不稳定。配置方式4为总投资一定时，不考虑机组暂态稳定边际成本，优先增加对系统暂态稳定裕量影响最大的机组，即η′（i）最大的机组的强励倍数。由表12可见，配置方式4下，系统暂态稳定，但系统暂态稳定裕量低于考虑边际成本的最优配置方案。配置方式3、4的结果进一步说明计算过程中优先增加暂态稳定边际成本最小机组的强励倍数的合理性。

4.2 系统2算例

系统2的数据见文献［19］，设置机组30和机组33采用静止励磁方式，其他机组采用无刷励磁方式。设置无刷励磁方式下 C0=1（MV·A）-1，静止励磁方式下 C0=0.9（MV·A）-1。设励磁系统总投资 Csum=10000，其他参数设置同4.1节算例。

4.2.1 考虑系统单一故障情况

系统考虑的主要故障为表2中故障E，主要故障E下机组强励倍数最优配置计算结果见表13，对应机组强励倍数见表14。

表13 发生单一故障时，系统2在不同强励倍数配置方案下的暂态稳定裕量Table 13 Transient stability margin of system 2 with single fault for different FEVR configurations

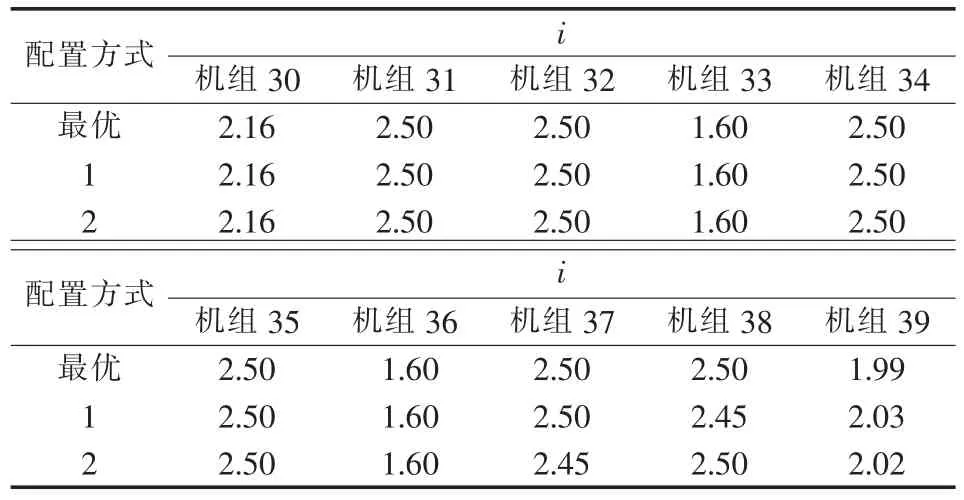
表14 发生单一故障时，系统2的强励倍数配置方案Table 14 FEVR configuration of system 2 with single fault

因系统额定配置下对故障E保持暂态稳定，表13中暂态稳定裕量是相对于额定配置的计算结果。对比表13、14中的计算结果，系统2考虑单一故障E时，在励磁系统总投资为10000的情况下按最优配置系统的暂态稳定性最佳。

4.2.2 考虑系统多故障情况

考虑系统多故障情况，故障选取表2中故障E和F，故障E和F的相对发生概率分别设为0.7和0.3。

多故障情况下，系统机组在强励倍数最优配置方式、配置方式1和配置方式2下对应的概率暂态稳定裕量见表15，相应的机组强励倍数见表16。由表15可知，系统2在励磁总投资为10000时，在最优配置下系统的概率暂态裕量最大。

表15 发生复合故障时，系统2在不同强励倍数配置方案下的概率暂态稳定裕量Table 15 Probabilistic transient stability margin of system 2 with multiple faults for different FEVR configurations

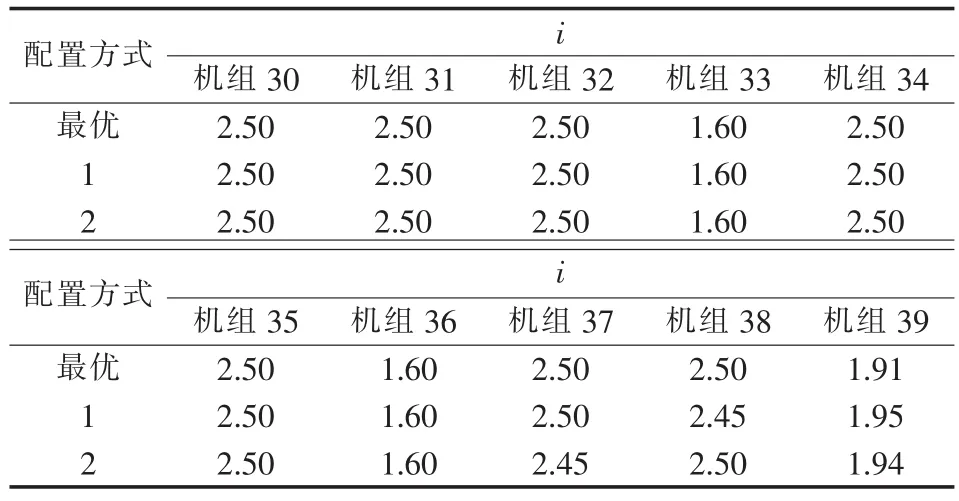
表16 发生复合故障时，系统2的强励倍数配置方案Table 16 FEVR configuration of system 2 with multiple faults

表17为保持其他参数不变，励磁系统总投资变化时对应最优配置下系统的概率暂态稳定裕量计算结果。励磁系统总投资一定时，采用强励倍数最优配置，系统暂态稳定性最佳。若最优配置下机组强励倍数可进一步增加，可以采用增加励磁系统总投资的方法进一步改善系统的暂态稳定性。

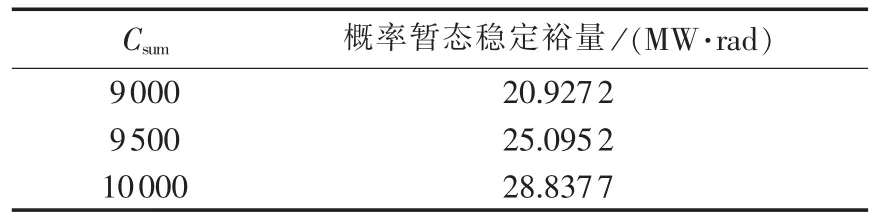
表17 采用强励倍数最优配置方案时，系统2在不同励磁系统总投资下的概率暂态稳定裕量Table 17 Probabilistic transient stability margin of system 2 with optimal FEVR configuration for different Csumvalues

5 结论

本文建立了无刷励磁方式对系统暂态稳定的线性关系影响模型及静止励磁方式对暂态稳定的二次多项式关系影响模型；考虑了静止励磁的饱和现象，和无刷励磁相比，饱和现象的存在使得静止励磁方式强励倍数的增加不能持续改善系统的暂态稳定性；提出了多机系统机组强励倍数优化配置算法，通过优化配置算法计算得到机组强励倍数最优配置。励磁系统总投资一定时，机组强励倍数最优配置使系统故障情况下的暂态稳定裕量最大，系统暂态稳定性达到最佳。