基于支持向量机的纯电动公交车充/换电站日负荷预测

刘文霞，徐晓波，周 樨

（华北电力大学 电气与电子工程学院，北京 102206）

0 引言

随着环境、能源问题的日益突出，电动汽车EV（Electric Vehicle）受到了各国政府的重视，电动汽车的大规模使用可以大量减少温室气体的排放，促进能源结构的调整［1-2］。文献［3-4］讨论了大量电动汽车负荷的接入对电网产生的影响，如大量电动汽车在负荷高峰期间充电，将加剧电网负荷的峰谷差从而增加调峰的难度，在配电网中会造成局部过负荷从而加重配电网的负担等，将对电网的安全、调度和经济运行产生不利影响。所以需要较精确的电动汽车负荷预测作为依据，进行电动汽车的有序充电控制，参与电力系统的调峰甚至调频。

根据使用能源和动力驱动系统的不同，电动汽车可以分为纯电动汽车PEV（Pure Electric Vehicles）、插电式混合动力汽车PHEV（Plug-in Hybrid Electric Vehicles）及燃料电池电动汽车。其中，纯电动汽车完全靠电能驱动；由于受电池容量限制，尚未大规模普及，但已成为中国电动汽车产业发展的重点，且通过科研和试点取得了一定的成绩。目前，在国内已有一些一定规模的纯电动公交车和出租车的试点。北京在奥运会后逐步增加了电动公交汽车的数量，采用换电方式，公交站也作为充换电站。目前的运行已经有了一定的规模，充电站的负荷也初步体现出了统计特征，在此背景下，开展充电站的负荷预测，为后续电动汽车有序充电管理系统提供有力支撑。

本文研究对象是公交汽车充电站日负荷预测方法。由于试点较少，国内外对纯电动汽车充电站负荷预测研究的文献不多［5-6］。文献［5］提出了模糊聚类和BP神经网络相结合的方法预测换电站的短期负荷。文献［6］采用蒙特卡洛的方法预测电动汽车充电负荷的时空分布特性。本文为预测充电站的日充电负荷曲线，借鉴了电力系统日负荷预测的方法。目前，电力系统日负荷预测方法主要分为2种：基于历史负荷数据的传统经典方法和基于历史负荷数据及其影响因素的机器学习方法。为了在预测模型中能更好地结合各种因素影响，提高预测精度，基于人工智能技术的神经网络预测模型和模糊预测模型得到了广泛的应用［7-9］。神经网络等机器学习方法是基于最小化经验风险的机器学习方法，但是在实际应用中，样本的数量总是有限的，此时经验风险最小并不意味着期望风险最小，如神经网络的“过学习”问题，在某些情况下，训练误差过小会导致推广能力的下降，即泛化能力变差。由Vapnik等人提出的基于结构风险最小化原理（SRM）的支持向量机SVM（Support Vector Machine）算法，以有限的样本信息在模型的复杂性和学习能力之间寻求最佳折中，以获得最佳的泛化能力。

由于SVM的参数对其性能影响很大，所以SVM用于预测的研究主要集中于预测模型参数的选择，目前确定参数的方法主要有2种，一种是经验或实验法选取［10-12］，另一种是使用遗传算法（GA）［13-14］、粒子群优化（PSO）算法［15］、微分进化［16］等优化算法确定。文献［10］的参数分析表明核参数p和正则化参数C对SVM的性能影响较大，当p和C固定于某一合适值时，SVM性能对不敏感损失参数ε不敏感。本文采用两阶段确定参数的方法：第一阶段对参数ε取定值；第二阶段采用GA对p和C寻优。

本文对北京市某电动公交车站的充电负荷特性进行了分析，确定了影响电动公交车充电负荷的主要因素，并根据这些因素，通过计算灰色关联度选取相似日建立小样本作为SVM模型的输入数据；介绍了SVM模型的回归算法、确定SVM预测模型的3个参数的方法和整个预测流程；使用公交换电站的充电负荷数据对本文的方法进行了验证。

1 纯电动汽车负荷特性分析

电动汽车的类型目前主要分为公交车、出租车、公共事业车、微型车和私人乘用车。电池的更换方式有整车充电和更换电池2种。充放电方式有单向无序充电、单向有序充电和双向有序充放电3种。电动汽车充电负荷的形成是由用户的行为引发，在充电设施处产生，因此充电负荷的分布具有时空特性，必须明确汽车在特定地点、特定时间的充电行为。影响电动汽车充电负荷的主要因素包括：用户的行为特性、电动汽车电池的充放电特性、电动汽车充电方式和电动汽车规模等。作为电动汽车充电负荷的触发侧，用户的行为特性对于确定电动汽车充电负荷至关重要。用户的行为特性包含电动汽车的类型、行驶里程、接入电网的时间、离开电网的时间、停放的场所等。天气情况、温度、节假日等外在因素也会影响用户的行为特性。

1.1 电动公交车充电站负荷特性分析

本文采集了北京某公交车充电站2012年7、8、9月的充电负荷数据，公交车规模30辆左右，目前，9 kW充电桩有240个，75 kW应急充电桩4个，充电方式为单向无序换电充电。

图1是该充电站2012年7月6日、7月7日和7月8日的日充电负荷曲线图。从该日负荷曲线可以看出，负荷峰值出现在 13∶00 — 14∶00 和 17∶00 —18∶00，所有充电在 23∶00 之前基本完成，此时开始没有负荷，一直持续到次日09∶00左右。

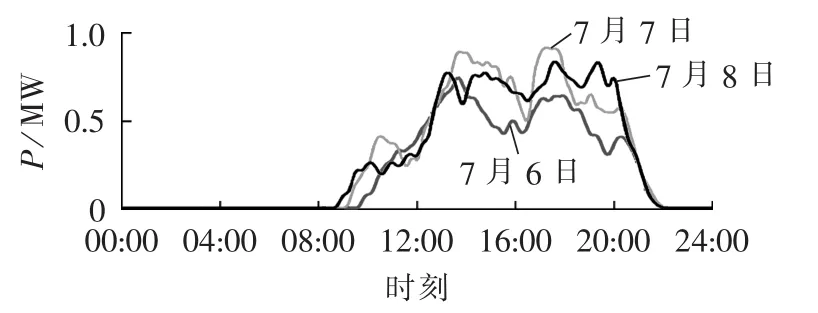
图1 电动公交车充电站日负荷曲线Fig.1 Daily load curves of electric bus charging station

通过对7、8、9月的充电负荷曲线（见图2）的观察，可以看出它们的变化趋势具有一定的相似性，表明了选取相似日进行负荷预测的可行性。

图3是2012年7月该充电站充电功率日最大峰谷差直方图。其中，最大峰谷差为1.065 MW，最小峰谷差为0.64 MW。峰谷差围绕0.8 MW上下波动，并且波动幅度较明显。图4是7月6日每5 min的短时波动量曲线。从图4中可以看出，在有充电负荷期间，短时波动量较大，最大值为37 kW，最小波动量接近为0，最小波动量和最大波动量之间的差值比较大。充电站充电负荷的短时波动较为明显。

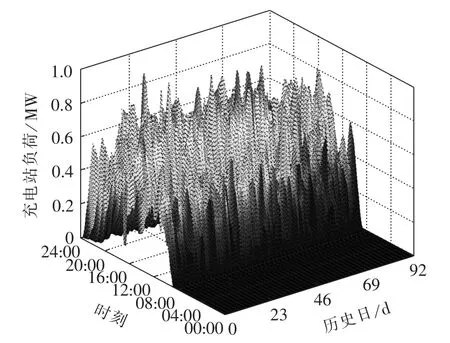
图2 电动公交车充电站3个月的日负荷曲线Fig.2 Daily load curves of electric bus charging station for three months

图3 日最大峰谷差Fig.3 Maximum daily peak-valley differences

图4 5 min负荷波动量Fig.4 Load fluctuations for 5 minutes

1.2 影响因素分析

电动公交车充电站的充电负荷是由电池充电产生，影响电池消耗速度的因素有很多，公交车所用电池型号一致，所以这里不考虑电池本身的特性。由于公交车行驶线路的固定，影响电池消耗的速度主要与当时的车速有关，而车速又与当时的车流量有关。文献［17］中叙述了影响车流量的因素，如温度、天气情况（晴、下雨等）等。结合现有数据，本文着重分析温度、日类型、天气情况、充电开始时间及充电结束时间对公交充电站充电负荷的影响。

图5是7月1日至9月30日的日最高温度（归一化值）和日平均负荷的散点图，为了证明日最高温度和日平均负荷之间的相关性，本文采用计算线性相关系数的方法衡量2个随机变量间的相关程度。计算公式如下：

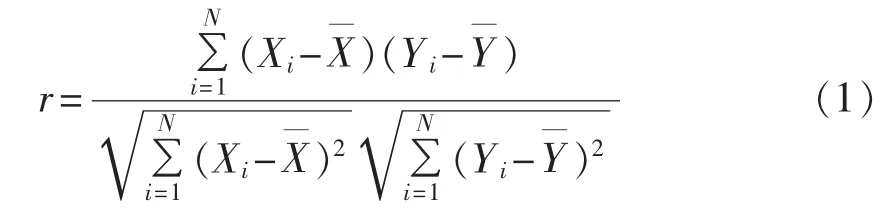
图5 日平均负荷与日最高温度散点图Fig.5 Scatter plot of daily average load and maximum temperature

其中，r为相关系数；Xi、Yi分别为第i日的最高温度和日平均负荷；分别为历史日最高温度和日平均负荷的平均值；N为历史日天数。当时，认为最高温度和日平均负荷有强相关性。

通过计算，日最高温度和日平均负荷的相关系数为0.800 2，表明最高温度和日平均负荷之间存在强相关关系。夏天当温度升高时，充电负荷也增加，其原因是天气炎热、公交车开空调，加快了电能的消耗，最终导致充电负荷的增加。

日类型和天气情况会影响用户的行为特性，进而影响充电站的充电负荷。由表1可以看出日类型对充电站负荷的影响不显著，这是由于公交车在工作日和非工作日的调度安排差别不大。但是，今后若调度安排改变，对于不同日类型，公交车的出行规律也不同，进而影响充电站的充电负荷曲线。为了使本文的模型更具泛用性，因此本文考虑日类型的影响。由表2可以看出下雨和无雨对充电站充电负荷有一定的影响。雨天的充电站充电负荷小于无雨天。此外，由图1可以看出充电站充电开始时间、充电结束时间不同，日负荷曲线白天从零开始上升、夜里下降为零的时刻也不相同，但是对于预测日，充电开始时间和充电结束时间无法得知。所以本文考虑的因素有最高温度、日类型和天气情况。

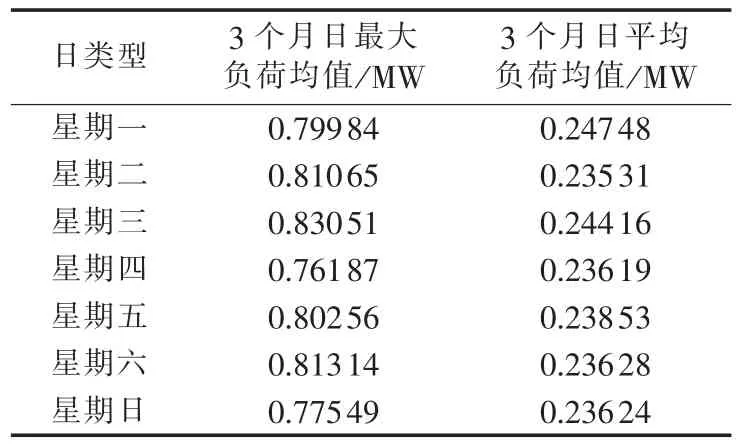
表1 不同日类型负荷分析Table 1 Load analysis for different day types

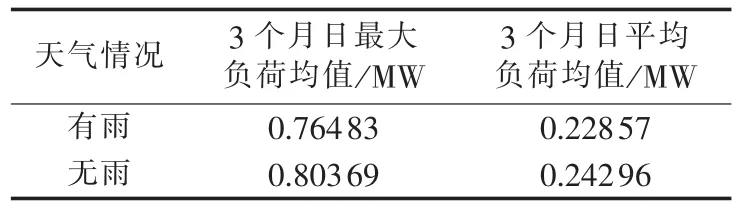
表2 不同天气情况负荷分析Table 2 Load analysis for different weathers

本文以最高温度的归一化值和日类型、天气情况的映射值作为特征量选取相似日。归一化公式如式（2）所示，日类型和天气情况的映射值分别如表3、4 所示。

其中，x′为某一天的最高温度；x′max为 7、8、9 月中最高温度；x为归一化后的值。

表3 日类型映射值Table 3 Mapping value for different day types

表4 天气情况映射值Table 4 Mapping value for different weathers

1.3 基于灰色关联度的样本筛选

通过选取相似日的方法，可以提高预测精度，也可以降低SVM样本训练时间。传统选取相似日的方法是基于人工经验的选取，常常会引入不良样本，增大预测误差。目前选取相似日的方法有证据理论［12］、聚类分析［18］、趋势相似度法［19］、灰色关联法［20］等。 本文采用计算灰色关联度的方法选取相似日。

采用灰色关联度分析方法选取相似日，本文计入的因素为最高温度、日类型和天气情况，使得训练样本和预测日之间在气象特征上具有较高相似性，可以提高预测精度。计算历史日n天的因素序列Xm=（xm（1），…，xm（t））与待预测日的因素序列 X0=（x0（1），…，x0（t））之间的相关度。其中，m=1，2，…，n；t是计入因素个数。

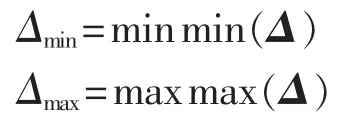
最后计算X0对Xm的灰色关联度：

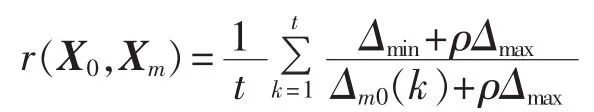
2 SVM回归模型及参数选择

2.1 SVM回归算法

SVM回归算法目前主要使用的是 v-SVM、ε-SVM和LS-SVR等算法。本文采用ε-SVM算法。

对于非线性负荷，通过非线性映射φ将每个样本点映射到高维空间，在高维空间中作线性回归。样本点如下：

其中，xi和yi分别为输入和输出量，其中xi为包括最高温度归一化值、日类型，天气情况映射值和相似日负荷值的向量，yi为真实值；l为样本点个数。

则非线性负荷的预测模型为：

其中，f（x）为模型输出的预测值；w为权向量；b为偏置。

根据Vapnik的最小化结构风险原则，其结构风险定义为：

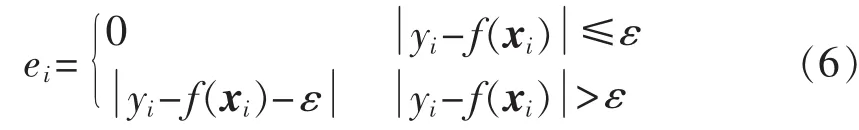
因此，ε-SVR的目标函数为：

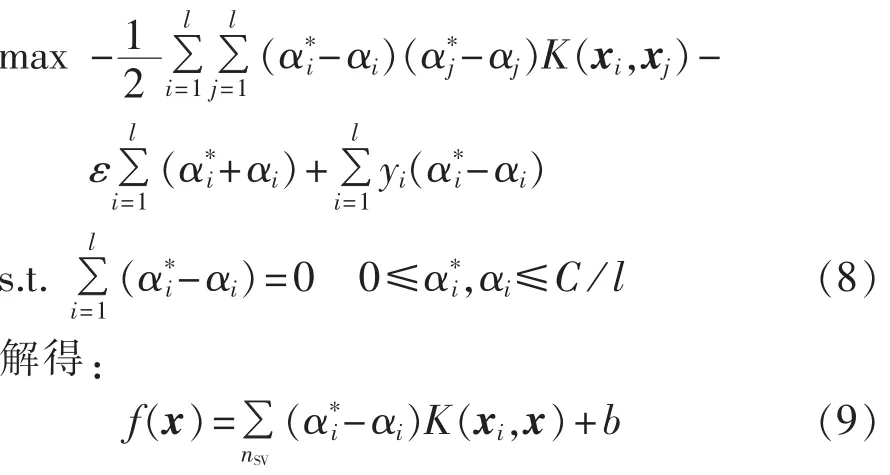
其中，nSV为支持向量的个数。由式（9）可以看出，只要知道核函数的形式即可进行预测，而不需要知道映射函数φ（x）和高维空间Rn。由于目前尚无理论指导选取核函数，常用的核函数有线性函数、多项式函数、径向基函数、多层感知器函数，因此，本文使用的是径向基核函数，如下式所示：

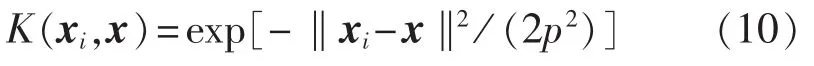
由式（8）可知，ε-SVR模型需要选择正则化系数C、参数ε和核参数p。

2.2 参数自适应

以9月1日至9月7日的相似日作为训练样本，以9月8日为测试样本，则当p在0.001～1范围内以步长0.05变化、C在0.1～40范围内以步长为2变化、ε在0.001～0.01范围内以步长为0.001变化时，试验1结果如表5所示。当C和p在上述范围内变化、ε=0.001时，试验2结果如图6所示。采用均方根误差（RMSE）进行评价：

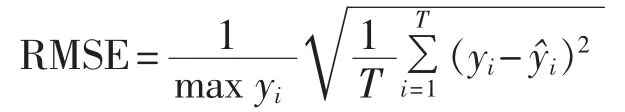
其中，T=1，2，…，96为日负荷预测总点数。

表5 随ε变化的平均RMSE值Table 5 Average RMSE for different ε values

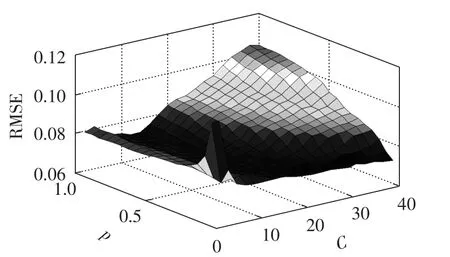
图6 RMSE随p和C的变化值Fig.6 RMSE varying along with p and C

试验1的RMSE均处于0.07～0.11之间，从表5可以看出，平均RMSE均处于0.082～0.083之间，RMSE变化较稳定。从图6中可以看出，当ε=0.001、C和p在上述范围内变化时，RMSE都处于0.07～0.11之间，变化不大，较稳定。可见参数ε对模型性能的影响不显著。因此，本文对ε取定值，由于参数ε在ε-SVR模型中控制着支持向量的稀疏性，ε越大，支持向量的个数就越少，当大于某一值时，就会出现“欠学习”现象，增大预测误差。本文令ε=0.001。

试验发现选取不合适的C和p，会对SVR的性能产生较大影响。所以本文使用GA确定参数C和p。GA不依赖于初始种群，通过复制、交叉和变异作用，具有较好的全局优化特性。步骤如下：

a.随机产生初始种群，个体数目取20，根据实际数据，分别从（0.1，40）和（0.001，1）范围内随机选取C和p的值；

c.选择轮盘赌策略，适应度高的个体被选中遗传到下一代的概率高，适应度低的个体可能被淘汰，然后对下一代的个体进行交叉和变异操作；

d.由新一代的种群返回步骤b，经过一定数量的迭代后，就会得到最优的C和p，即所选的C和p使得结构风险最小。

表6选取了3组训练样本进行收敛性分析（训练样本的形成见算例验证部分），每组数据重复上述4个步骤300次，记录下每次最终的适应度作统计，如数据1，除去一些明显的异值，剩下的数据的个数占总的数据个数的93%，其均值为1.9392，方差为0.00072。由表6可知，GA具有较好的收敛性。

表6 收敛性分析Table 6 Convergence analysis

2.3 预测流程

预测流程如下：

a.采用五点滑动平均［21］的方法对充电负荷数据进行预处理，然后再对负荷数据、影响因素数据进行归一化；

b.采用计算灰色关联度的方法选取关联度最大的3天为待预测日的相似日，相似日的负荷数据和因素数据共同构成训练样本和测试样本，作为ε-SVR模型的输入；

c.使用GA选取最佳正则化参数C和核参数p；

d.利用ε-SVR模型进行电动汽车充电站的日充电负荷预测。

具体流程图如图7所示。

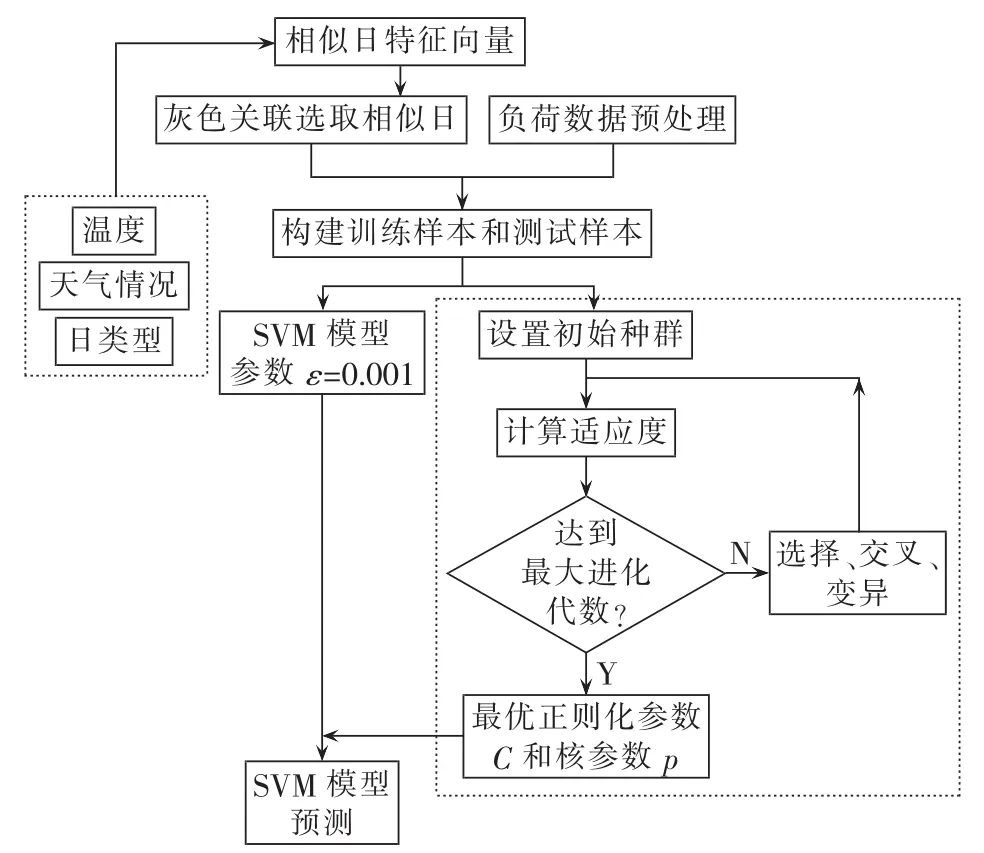
图7 充电负荷预测流程图Fig.7 Flowchart of charging load forecasting

3 算例验证

对北京市某公交换电站进行96点的日充电负荷预测，以2012年7月1日至8月31日的充电负荷数据为历史数据，以9月1日至9月7日为训练样本，9月8日为测试样本，再以7月2日至9月1日为历史数据，9月2日至9月8日为训练样本，9月9日为测试样本，依此类推，将最新的信息放入模型中。采用RMSE进行评价，所得的预测结果如表7所示。

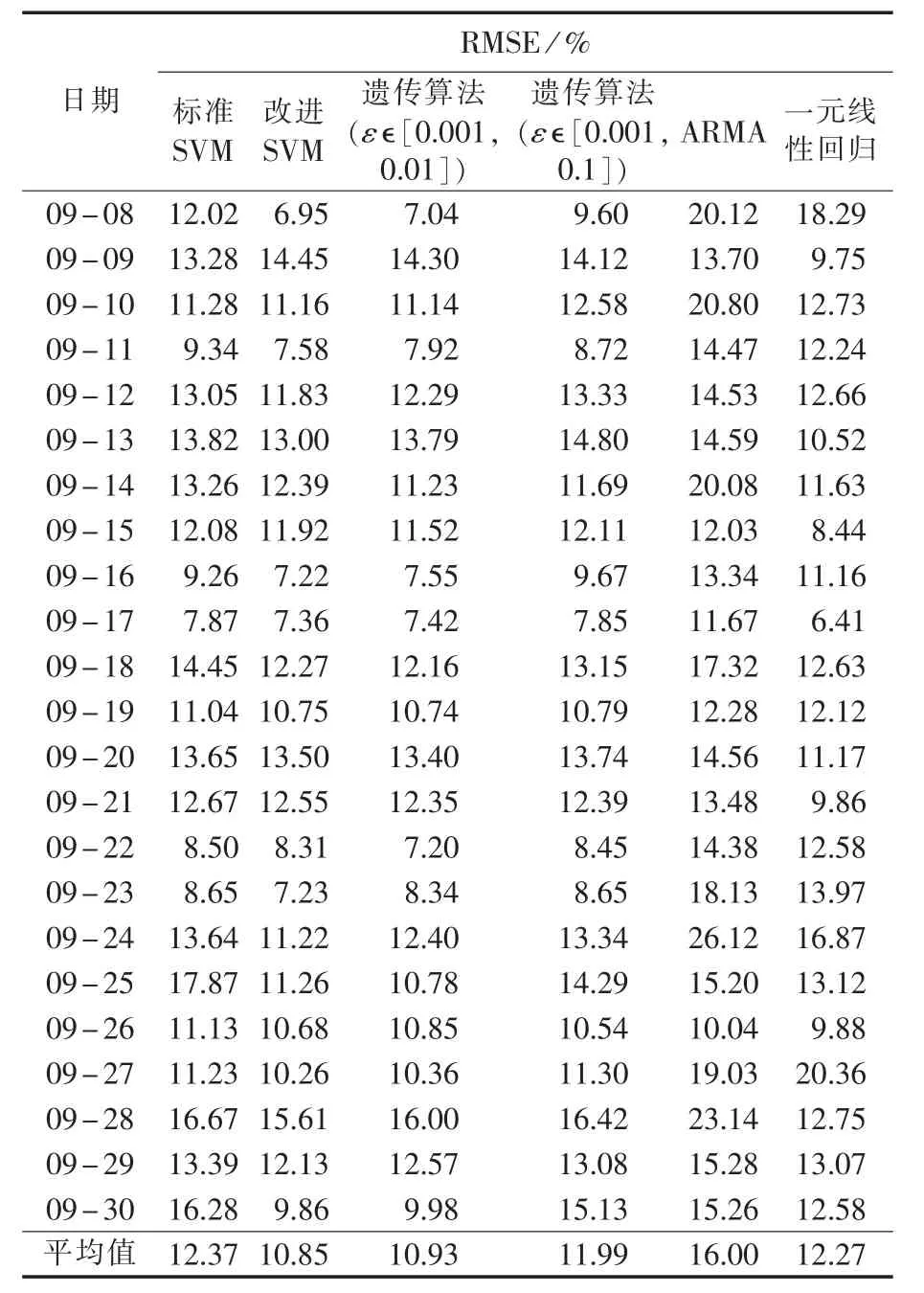
表7 预测结果Table 7 Results of forecasting

从表7可以看到，使用标准SVM得到的预测误差，最大为17.87%，最小为7.87%，平均为12.37%，采用本文的方法，得到的预测误差最大为15.61%，最小为6.95%，平均为10.85%，基本满足预测要求。相比于标准SVM得到的预测结果，本文方法的精度提高了1.52%。

当 C 在 0.1～40之间、p在 0.001～1之间、ε在0.001～0.01之间时，使用GA对以上3个参数寻优时，得到的预测误差最大为16%，最小为7.04%，平均值为10.93%，由表7可以看出预测结果和本文提出的方法接近。

当 C 在 0.1～40之间、p在 0.001～1之间、ε在0.001～0.1之间时，使用GA对以上3个参数寻优时，得到的预测误差最大为16.42%，最小为7.85%，平均误差为11.99%。由表7可以看出当参数ε选取的寻优范围不合理时，会降低预测的精度。

表7的最后2列是采用传统的ARMA和一元线性回归方法得到的预测结果。由于充电站充电负荷的波动性较大，使得ARMA和一元线性回归的预测误差较大。在这23天中，ARMA的RMSE最大为26.12%，最小为10.04%，平均值为16%，波动范围为16.1%；一元线性回归的RMSE最大为20.36%，最小为6.41%，平均值为12.27%，波动范围为13.95%；而本文的改进SVM方法的RMSE最大为15.61%，最小为6.95%，平均值为10.85%，波动范围为8.66%；可见本文的方法具有较好的预测精度和稳定性。

图8为采用本文方法预测的9月8日和9月28日的充电站充电负荷曲线图。9月8日的预测误差最小，RMSE为6.95%；9月28日的预测误差最大，RMSE为15.61%。

图8 电动公交车充电站日负荷预测误差最小/最大日图Fig.8 Actual and forecast daily load curves of electric bus charging station for minimum and maximum forecasting error days

4 结论

a.本文结合现有数据，分析了影响充电站公交车充电负荷的主要因素。对原始数据进行了预处理，减少了坏数据对预测结果的影响，并采用灰色关联方法选取相似日，增加了数据的相关性，采用基于结构风险最小的SVM方法进行建模，具有全局最优的优点和更好的泛化性能。通过实例表明了公交车充电站的日负荷预测精度平均可达10.85%，预测时间在5 min之内，能基本满足电动汽车充电有序控制的要求。

b.对于SVM模型，本文采用了两阶段确定模型参数的方法，与标准的SVM模型相比，预测精度提高了1.52%；当学习参数ε的选取范围较大时，改进方法的预测精度与3个参数同时寻优的方法相比，提高了1.14%。同时与传统的ARMA和一元线性回归方法相比，采用本文的方法具有较好的预测精度和稳定性。

c.目前公交电动车数量不多，公交电动充换电站的充电负荷数据的统计特性不明显，预测误差较大。随着国家对电动汽车的推广，充换电站的充电负荷数据的统计特性会越来越明显，未来本文方法的预测精度将会进一步提高，为电动汽车的有序控制提供强有力的支撑。