考虑扰动源定位的电压暂降监测点最优配置
2014-09-27陈礼频肖先勇张文海
陈礼频,肖先勇,张文海
(1.四川大学 电气信息学院,四川 成都 610065;2.四川大学 智能电网四川省重点实验室,四川 成都 610065)
0 引言
电压暂降是系统运行过程中不可避免的短时电能质量扰动现象[1-2]。随着电力电子、微电子等技术的推广应用,因电压暂降导致的用户抱怨和经济损失日益严重,已引起国内外学者的广泛关注[3-7]。国际电气与电子工程师协会(IEEE)将电压暂降定义为:电压有效值降至额定电压的10%~90%,持续时间为0.5周期到1 min的短时扰动现象[8]。电压暂降是供电企业和用户面临的最严重的电能质量问题之一[9],而在线监测是统计分析电压暂降的有效方法,也是供电企业和用户的迫切要求。系统故障是电压暂降最主要的扰动源[10],本文针对系统故障引起的电压暂降,研究监测点的优化配置方法。
现有电压暂降统计分析方法主要有随机评估法和实测统计法[11]。随机评估法通过建立随机模型评估电压暂降特征,具有推广性和预测性。但电压暂降受故障位置、系统元件故障率、气候环境以及保护可靠性等因素影响,具有复杂不确定性[12-14],而实际中通常缺乏这些影响因素的统计信息,这直接影响着随机评估结果的准确性。实测统计法基于监测装置记录的测量数据,能保证统计结果准确、可靠,但实际中不可能在所有母线安装监测装置。因此,通过优化配置监测点,以最少监测点实现全网电压暂降可观,具有重要的工程实用价值。
传统电压暂降监测点配置方法基于监测点可观测域 MRA(Monitor Reach Area)原理[15-18],根据给定电压阈值配置监测点,存在电压阈值选取困难和非监测点电压暂降特征信息删失等问题。以定位电压暂降扰动源为目标配置监测点,是解决上述问题的有效途径。然而现有相关方法尚不完备:文献[19]在一组确保全网电压暂降可观的监测点配置方案基础上,通过增加监测冗余度,扩大全网故障可观范围,但该方法不能保证以最少的监测点数定位电压暂降扰动源;文献[20]未考虑监测装置只记录幅值低于设定阈值的电压暂降事件,而实际中监测装置由于存储空间有限,不可能对电压一直录波。
本文首先保证全网幅值低于0.9 p.u.的电压暂降可观,在此基础上充分利用暂降幅值特征信息,基于节点阻抗矩阵定位扰动源,建立反映各监测点组合可定位扰动源范围的扰动源可观性矩阵。用0-1整数线性规划方法进行监测点优化配置,实现对全网电压暂降及其扰动源的有效观测。对IEEE30节点测试系统的仿真证明了本文方法的正确性、有效性和工程应用价值。
1 电压暂降幅值计算模型
如图1所示,假设m为被观测母线,λ为线路i-j上故障点k到节点i的距离。m与k之间的互阻抗和k的自阻抗分别为:

其中,上标 u取值 1、2、0表示正序、负序和零序;Zumi、Zumj和 Zuij为节点间互阻抗;Zuii、Zujj和 Zukk为节点自阻抗;zuij为线路i-j的阻抗值。
设各节点故障前电压均为1 p.u.,旋转因子α=ej120°。当k点发生不同类型短路故障时,母线m的电压暂降幅值计算公式见式(3)—(6)。
三相短路故障:

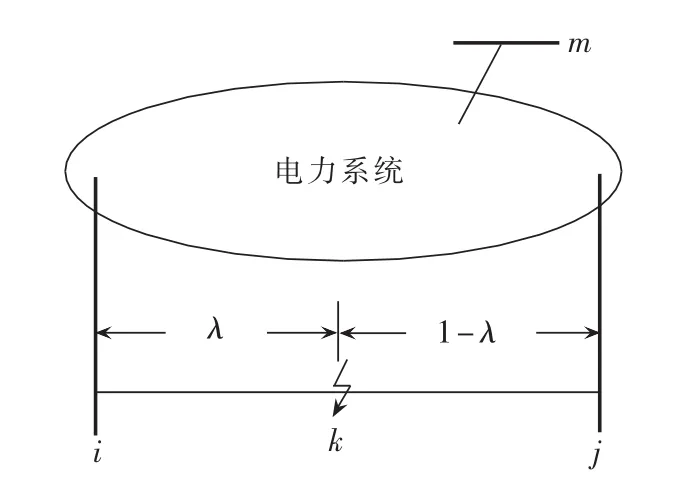
图1 系统结构Fig.1 Structure of power system
单相接地短路故障:
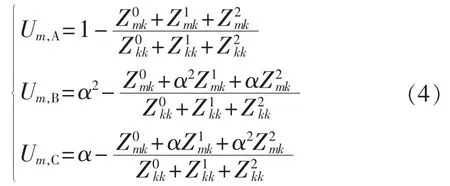
两相短路故障:
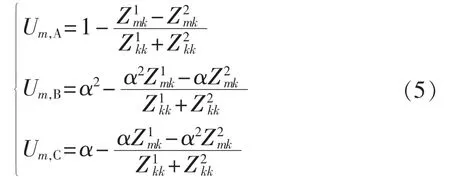
两相接地短路故障:
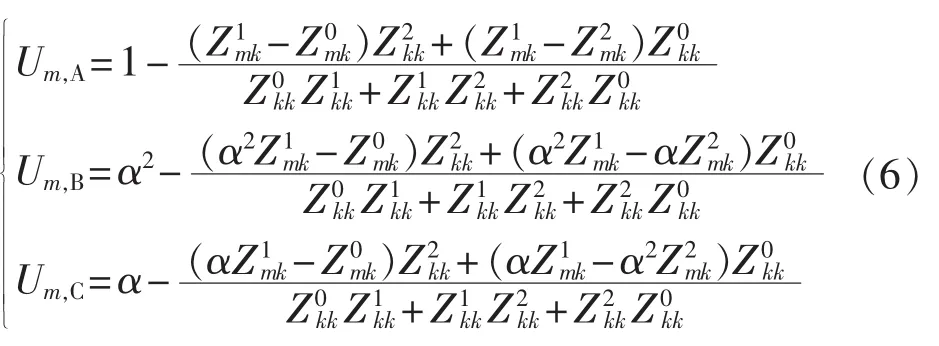
2 传统监测点配置方法及其不足
2.1 传统方法原理
传统监测点配置方法基于MRA原理,比较短路计算所得电压幅值与设定的电压阈值,设p为全网设定的故障点数(或用解析式法求出的全网线路分段数)[18],n为全网母线数,则电压暂降可观性矩阵为:
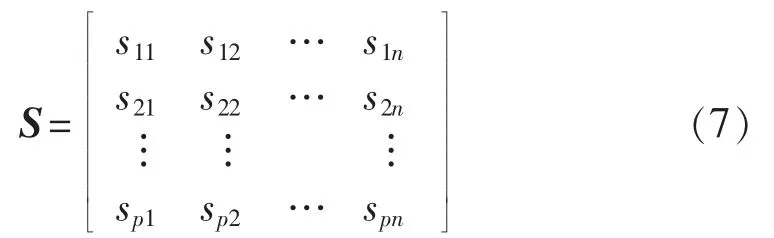
S中任意元素sij取值为:
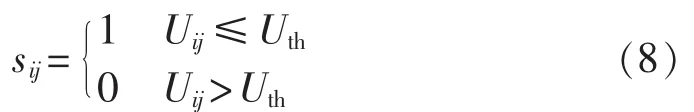
其中,Uij表示第i个故障点(或线路分段)发生短路故障时母线j的电压,不对称故障取幅值最小一相电压;Uth为设定的电压阈值。
定义n维监测点决策向量:
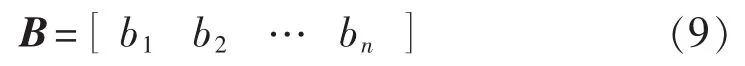
B中元素取值为:

为确保全网电压暂降可观,对S中任意第i行元素,B中元素均应满足不等式约束:
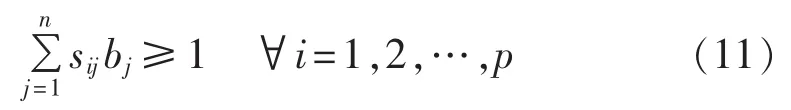
为使监测点数最少,则目标函数为:

采用0-1整数线性规划方法求解式(11)、(12)构成的优化问题,即可得出保证全网电压暂降可观的监测点配置方案。
2.2 传统方法的不足
a.电压阈值Uth选取困难。
采用传统监测点配置方法,Uth越大所需监测点越少,反之所需监测点越多。Uth选取过大,监测点不能对全网中幅值较小的电压暂降进行有效监测,而这些暂降往往是更应受关注的严重扰动事件;Uth选取过小,则需安装较多的监测装置,经济成本相应增加。监测电压暂降的最终目的,是为反映敏感设备受扰动的严重程度。然而电网中各敏感设备的电压耐受能力不同,且敏感设备对电压暂降的响应具有时空变化特性[21-22]。因此,传统方法基于给定的Uth配置监测点,存在Uth选取困难的问题。
b.非监测点电压暂降特征信息删失。
如图2所示,传统监测点配置方法仅将电压用于判断是否低于Uth,而未充分利用具体的电压幅值信息。监测点配置方案是估计非监测点电压幅值特征的基础,如图3所示,电压暂降状态估计需根据监测点电压估计各线路分段故障次数,再计算非监测点电压[23]。然而线路上不同位置发生故障引起的电压暂降幅值差异明显,以线路段为单元估计非监测点电压,对暂降幅值特征的刻画过于粗糙,必然导致暂降幅值特征信息的删失。

图2 电压暂降可观性矩阵的构建原理Fig.2 Principle of voltage-sag observability matrix construction
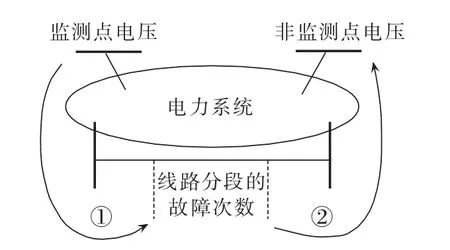
图3 电压暂降状态估计原理Fig.3 Principle of voltage-sag state estimation
针对以上问题,本文充分利用电压暂降幅值特征信息,同时考虑到实际中监测装置只记录幅值低于设定阈值的电压暂降事件,提出能保证全网电压暂降及其扰动源位置可观的监测点配置方法。
3 考虑扰动源定位的监测点配置方法
3.1 保证全网电压暂降可观的所有配置方案
电压暂降是电压有效值降至额定电压10%~90%的短时扰动事件,监测装置基于设定阈值触发并记录暂降数据。实现电压暂降扰动源定位的前提是能记录到电压暂降数据,考虑到电压暂降的定义及电能质量监测装置记录暂降数据的实现原理,本文首先基于MRA原理并设Uth=0.9 p.u.配置监测点,作为定位扰动源的初始配置方案,以确保全网中任意母线发生电压暂降时,监测装置能记录到电压暂降数据。由式(11)、(12)确定的监测点配置方案往往并非唯一,可用0-1整数线性规划方法先求出一组配置方案,将该方案以式(13)、(14)的形式作为求解下一组方案的新增约束条件,按图4所示流程循环求解,即可求出满足式(11)、(12)的所有监测点配置方案。

其中,YS,min为用0-1整数线性规划方法求得的最少监测点数;Bt-1表示前次计算所得配置方案。式(13)确保监测点总数维持为 YS,min,式(14)确保新方案与之前求出的方案不重复。
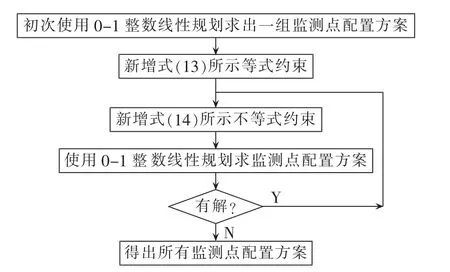
图4 用0-1整数线性规划方法求取所有配置方案Fig.4 All allocation schemes solved by 0-1 integer linear programming
3.2 基于节点阻抗矩阵的扰动源定位法
系统中不同位置发生短路故障,母线电压暂降幅值不同[24]。因此,可根据母线电压暂降幅值,应用数值计算方法反解求出扰动源位置。以三相短路故障为例,当故障点k未知时,由式(3)建立方程:
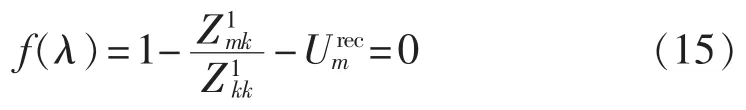
其中,Umrec为监测点m处电压暂降幅值。用弦割法[25]求解该方程,迭代公式为:
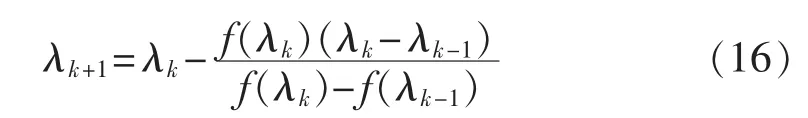
当多个监测点同时记录到电压暂降时,可建立多个式(15)形式的方程,共同构成一超定非线性方程组,可用最小二乘法[26]求解 λ。
由于扰动源所在线路未知,需遍历所有线路求解扰动源位置,因此求出的解中可能含有伪故障点。此时,可通过增加监测点以唯一确定扰动源位置,在数学上即为通过增加等式约束保证解的唯一性。然而盲目增加监测点,不仅增加了成本,且仍难排除伪故障点,因此需对监测点进行优化配置。
3.3 监测点优化配置方法
应用3.1节方法,假设共求出c0组监测点配置方案,各组方案均能保证全网中幅值低于0.9 p.u.的电压暂降可观,将这些方案表示为:

以O为初始所有监测点组合,从全网n个节点中选取x个节点与O中各组合构成新的监测点组合,新组合总数为:

其中,Cnx为从n个节点中选取取x个节点的组合总数。
将所有新组合表示为监测点组合向量:
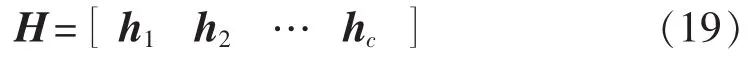
H中各监测点组合包含的监测点为:
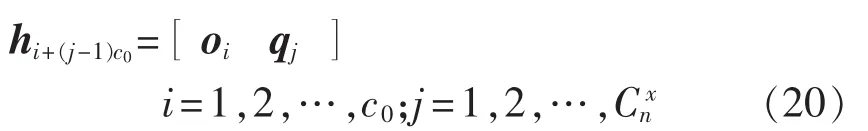
其中,oi为O中第i组组合;qj为第j组从n个节点中选出的含x个节点的组合。H中各组合可能含有重复监测点,但不会影响最后结果。
排除伪故障点后唯一确定电压暂降扰动源位置,称为扰动源可观,定义扰动源可观性矩阵:

其中,w表示故障类型;Fw为g×c维矩阵;g为全网中设置的故障点数;c为监测点组合数。Fw中元素取值为:
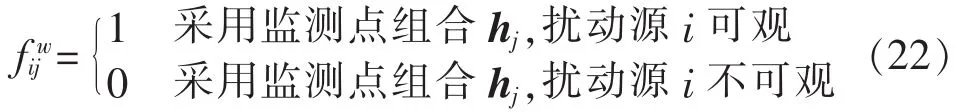
用Fa表示考虑了所有故障类型的扰动源可观性矩阵,其维数与Fw相同。Fa中元素取值为:
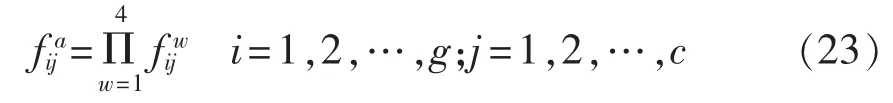
Fa中第j列元素表示第j组监测点组合可定位的扰动源范围。若Fw中第i行元素全为0,表示当前所有监测点组合均不能唯一确定扰动源i的位置,则需增加监测点数量。O中各组合新增的监测点数x从0开始逐步增加,直到Fa中各行至少一个元素不为0为止。
定义c维监测点组合决策向量:

D中元素取值为:

为保证全网电压暂降扰动源可观,对Fa中任意第i行元素,D中元素均应满足不等式约束:

为使监测点数最少,需求出最少的监测点组合数:

类似图4思想,用0-1整数线性规划方法求出满足式(26)、(27)的所有解,其中监测点数最少的方案即为最优方案。
综上所述,考虑扰动源定位的电压暂降监测点最优配置实现流程见图5。
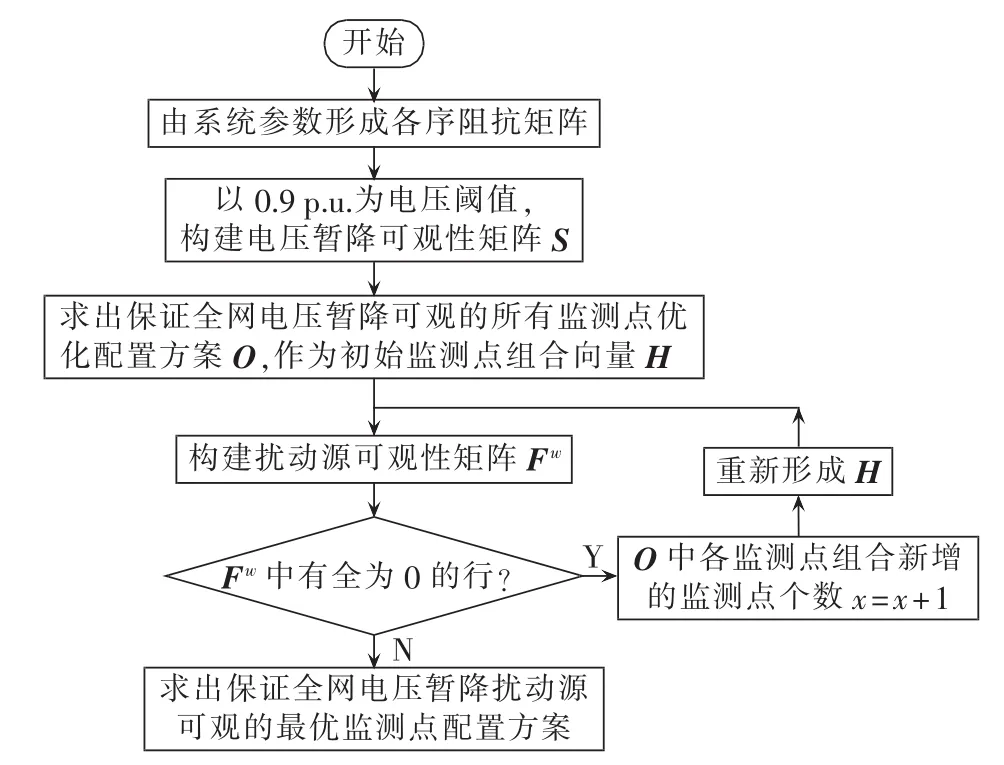
图5 考虑扰动源定位的电压暂降监测点最优配置Fig.5 Optimal allocation of voltage-sag monitoring points considering disturbance-source locating
如图5所示,本文方法只需监测到全网中有电压暂降发生,并以其扰动源可观为约束进行监测点优化配置,无需同传统方法一样通过降低Uth以实现对较小幅值电压暂降的监测,因此不存在传统方法中电压阈值选取困难的问题。应用本文方法配置监测点,电网中发生电压暂降后,可根据监测点记录的电压暂降数据确定扰动源位置,然后通过短路计算[9]即可准确得出非监测母线电压,因此克服了传统方法造成的非监测母线电压暂降特征信息删失的问题。
4 算例分析
4.1 本文方法的验证

图6 IEEE 30节点测试系统Fig.6 IEEE 30-bus test system

表1 保证全网电压暂降可观的监测点配置方案Tab.1 Allocation scheme ensuring grid-wide observability of voltage sags
应用本文方法对图6所示IEEE 30节点测试系统[10]进行仿真。按图5所示流程,首先以0.9 p.u.为电压阈值,求取保证全网电压暂降可观的所有监测点配置方案,结果见表1。IEEE 30节点测试系统共37条线路,每条线路上等间距取10个故障点(实际中可根据线路长度选取故障点数),以表1中所有方案作为初始监测点组合,构建370×18维扰动源可观性矩阵Fa。构建Fa
时需遍历全网线路求解扰动源位置,用解出的扰动源位置计算监测点电压,比较监测点计算电压值与实际电压值,当各相电压之差均小于0.001 p.u.时,才认为该扰动源位置是可行解。按图5求出保证全网电压暂降及其扰动源可观的监测点配置方案,结果见表2。为验证本文方法实用性,在每条线路上等间距取100个故障点,用表2中方案对扰动源定位。定义扰动源可观率为:

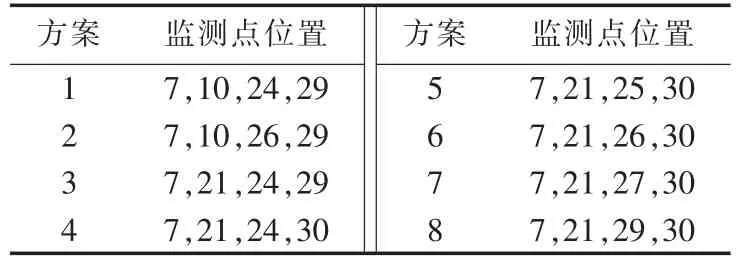
表2 保证全网扰动源可观的监测点配置方案Tab.2 Allocation scheme ensuring grid-wide observability of disturbance sources
表2中各方案的扰动源可观率如表3所示,可见所有方案最低的扰动源可观率也可达到98.27%,由此验证了本文方法的正确性和实用性。
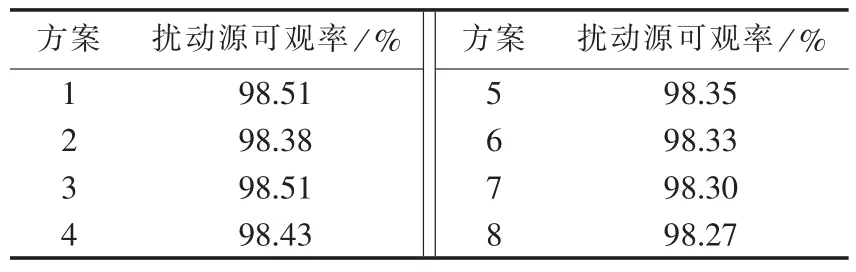
表3 最终监测点配置方案的扰动源可观率Tab.3 Disturbance source observability rates of final scheme
4.2 监测点数量比较
表4所示为采用传统方法设置不同电压阈值(标幺值)时,全网所需监测点数。

表4 传统方法不同电压阈值所需监测点数Tab.4 Monitoring points required by traditional methodfor different voltage thresholds
表4中,传统方法采用0.9 p.u.为电压阈值时,虽只需 2 个监测点,但根据电压暂降域原理[10,16]可知,此时监测点对幅值较小的电压暂降存在监测盲区。因此,采用传统方法配置监测点,若电压阈值设置过高,监测点对全网电压暂降的监测能力有限,可获取的暂降特征信息少。由表4知,随着电压阈值的降低,为保证全网中无监测盲区,所需监测点数量明显增多。表2中本文方法仅需4个监测点,即可保证全网电压暂降及其扰动源位置可观,根据扰动源位置经短路计算便能得出非监测母线电压幅值,克服了传统方法中电压阈值选取困难的问题,鲁棒性更好。
4.3 本文方法的应用
在每条线路上等间距设定100个三相短路故障点,用表2中方案1进行监测。任选非监测母线11—20,应用本文方法统计得出不同电压幅值(标幺值)电压暂降次数如表5所示。实际应用时,幅值统计区间可根据需要调整。
本文方法通过确定各扰动源位置,经短路计算得出非监测母线电压暂降幅值特征。而传统方法无法如本文方法一样对单个电压暂降的特征进行准确刻画,导致非监测母线电压暂降特征信息删失。
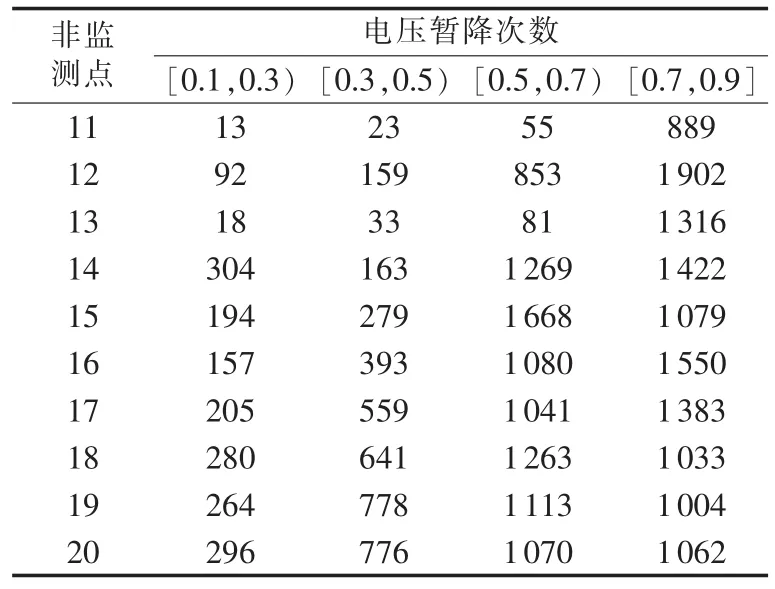
表5 非监测点电压暂降统计Tab.5 Statistics of voltage sag at non-monitoring points
此外,对于表1中方案,即使不具备条件增加监测点数量以实现全网电压暂降扰动源可观,仍可应用本文方法实现对监测点数据有效利用,并选出最佳配置方案。图7为表1中18组方案对应的扰动源可观率,可见方案17的扰动源可观率最高,为最佳配置方案。同理,对于已安装有监测装置的系统,可应用本文方法实现对监测数据的有效利用。
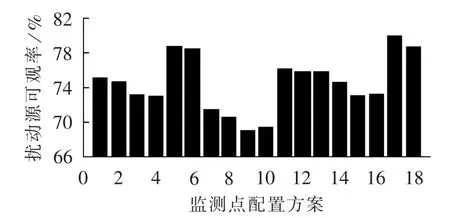
图7 初始18组监测点配置方案的扰动源可观率Fig.7 Disturbance source observability rates of initial 18 schemes
5 结论
a.基于扰动源可观性矩阵和监测点最优配置模型,对电压暂降监测点进行优化配置,保证了全网电压暂降及其扰动源位置可观。
b.对IEEE 30节点测试系统的仿真结果表明,本文方法正确、有效,所需监测点数量少,克服了传统方法电压阈值选取困难的问题,具有较好的鲁棒性,且能更精确刻画非监测母线电压暂降特征。
c.如何考虑发电计划、负荷波动、电网拓扑结构变化等因素对监测点配置的影响,将是下一步研究的重点。
