定转子电阻对同步电机瞬态时间常数影响

2014-09-27许国瑞赵海森刘晓芳

电力自动化设备 2014年6期

许国瑞，赵海森，刘晓芳

（华北电力大学电气与电子工程学院，北京 102206）

0 引言

实验室通常采用与大型电机相同结构等比例缩放的小功率同步电机模拟和研究大型发电机的动态特性[1-4]。但是与大型发电机相比，小功率同步电机定转子电阻的标幺值并非远小于相应绕组漏电抗，若在计算小功率电机瞬态时间常数时仍采用忽略定转子电阻的传统解析方法进行计算，必然会产生一定误差。因此，有必要探讨传统计算大型发电机瞬态时间常数的方法能否直接用于小功率电机的动态特性计算。

在研究大型电机动态过程时，由于定、转子电阻标幺值相对其漏抗很小，在计算直轴瞬态时间常数时通常忽略定子电阻，计算定子非周期瞬态时间常数时通常忽略转子电阻[5-7]。同样，在对小功率电机进行动态研究时，部分文献也采用这种忽略电阻的方法[8]，然而受容量、尺寸等条件限制，小型电机定、转子电阻值（标幺制）远大于实际大型发电机。对比本实验室7.5 kW同步电机、文献[5]中1000 kW同步电机和电力系统300 MW发电机的原始参数发现：7.5 kW电机与300 MW电机对应参数的数值比分别是定子电阻12.5，定子漏抗0.206，转子电阻6.67，转子漏抗0.34；1000 kW电机与300 MW电机对应参数的数值比分别是定子电阻5.3，定子漏抗0.667，转子电阻2.8，转子漏抗1.6。显然，小型电机具有定、转子电阻值偏大，而漏抗值偏小的特点，而瞬态时间常数是描述电机瞬态和动态行为的重要参数[9]。因此，研究定转子电阻对瞬态时间常数的影响意义重大。

同步电机的瞬态参数是描述电机瞬态和动态行为的重要参数，是基于三相突然短路定义的[10]。三相突然短路试验是测取同步电机瞬态参数较为理想的方法，也是国家标准推荐采用方法[11]。因此文中主要基于空载三相突然短路对瞬态时间常数进行研究。

本文首先推导空载三相突然短路后计及定转子电阻的励磁电流和瞬态时间常数的改进解析表达式，再通过7.5 kW模型机试验及时步有限元验证该解析式的正确性，最后将该解析式用于不同功率电机，计算不同定转子电阻时电机瞬态时间常数，得出改进解析式计算精度明显高于传统解析式。研究结果为瞬态时间常数的计算和精确测量提供理论基础。

1 研究方法

1.1 改进解析表达式

在文献[12]的基础上，得到不计阻尼作用时的同步电机直轴运算电抗如下：

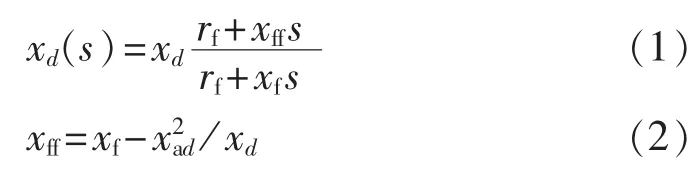
其中，xd为直轴同步电抗；xad为直轴电枢反应电抗；rf和xf分别为励磁绕组的电阻和电抗。

在忽略阻尼作用的情况下，交轴运算电抗为：

其中，xq为交轴同步电抗。

同步电机三相突然短路后直轴电流的拉普拉斯变换式[12]为：

其中，Em为空载电动势的幅值；rs为定子电阻。

励磁电流的拉普拉斯变换式与直轴电流的拉普拉斯变换式之间满足如下关系：

因此励磁电流的拉普拉斯表达式可变为：

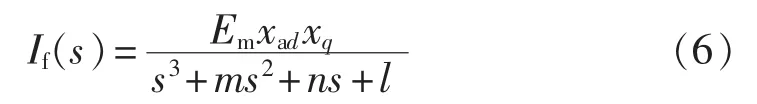
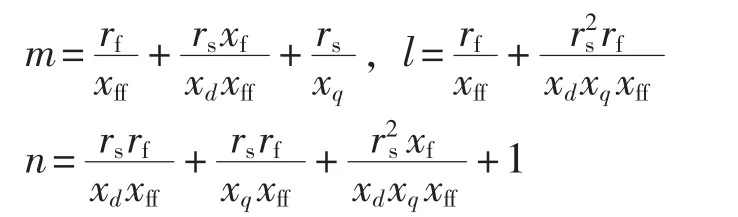
为对式（6）进行拉普拉斯反变换，需将分母因式分解，即令：

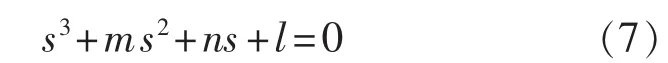
据卡丹公式[13]令 s=y-m/3 代入式（7）消二次方得：

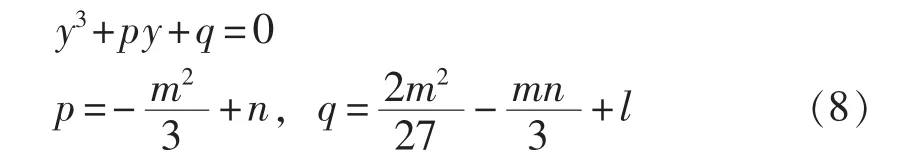
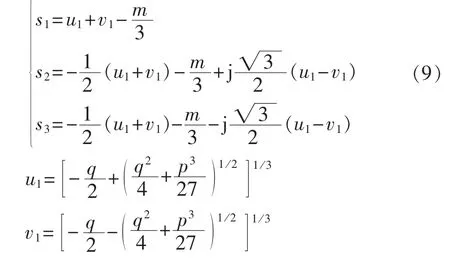
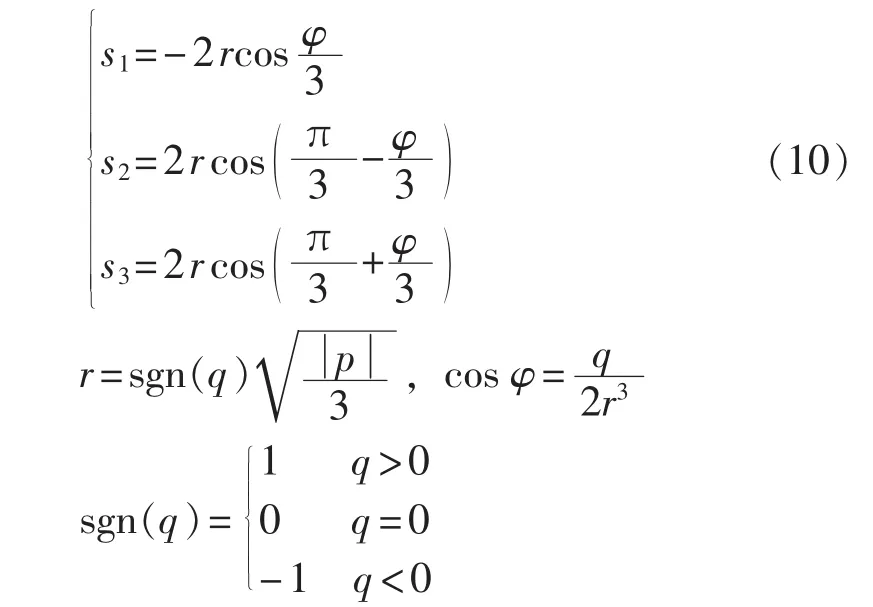
将励磁电流进行拉普拉斯反变换后可以得到2种励磁电流的时域表达式：

其中，uf为励磁电压；A1、A2、B1、B2、C 为励磁电流不同分量的幅值。

对比式（11）和式（12）知，式（11）中既有交流衰减分量，又有直流衰减分量，而式（12）中只有直流衰减分量。因此式（11）和（12）的直轴瞬态时间常数为：

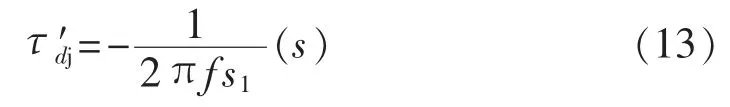
其中，f为电网频率。

式（11）中有定子非周期衰减时间常数，而式（12）无，因此式（11）中的定子非周期衰减时间常数为：

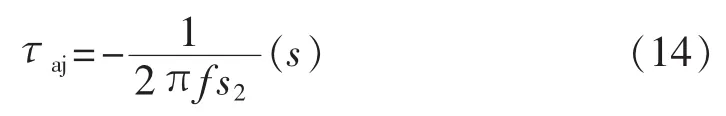
通过上述分析发现，计及定转子电阻的励磁电流改进表达式存在2种形式，由此可知随着定转子电阻的不同，改进的瞬态时间常数也会发生变化。

1.2 瞬态时间常数的传统表达式

电力系统分析以及电机瞬态理论中对瞬态时间常数定义如下[12]。

传统的直轴瞬态时间常数如式（15）所示：

其中，x′f为转子仅有励磁绕组，当电枢绕组短路时从转子绕组端看的瞬态电抗。

传统的定子非周期衰减时间常数如式（16）所示：

其中，x′d为直轴的瞬态电抗。

空载三相突然短路励磁电流传统解析表达式：

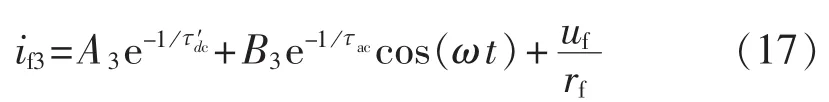
电力系统常用的2～6阶实用模型[19]均采用传统方法得到的τ′dc、τac。

1.3 时步有限元模型

时步有限元法（T-S FEM）是结合磁场方程与绕组回路方程得到[14]，该模型能够充分考虑发电机磁路饱和、磁场畸变、谐波磁场和集肤效应等的作用，可为发电机动态运行工况提供标准响应[15]。

为了验证该时步有限元模型的精确性，对实验室7.5 kW模型机进行时步有限元仿真计算并与试验进行对比，结果如图1所示。可见，7.5 kW电机空载三相突然短路的时步有限元仿真与实测曲线非常吻合。时步有限元很好地计及电机内部的复杂非线性、磁场畸变等因素，它能有效地反映发电机稳态、暂态等运行行为，是一种比较精确的仿真工具。

图1 空载突然短路时时步有限元仿真与试验对比Fig.1 Comparison between T-S FEM and test for sudden short circuit without load

2 瞬态时间常数的对比分析

2.1 7.5 kW同步发电机模型机

本文采用一台两极7.5 kW同步发电机模型机对瞬态时间常数进行理论和试验研究。模型机二维平面结构如图2所示，表1为发电机的基本结构数据。

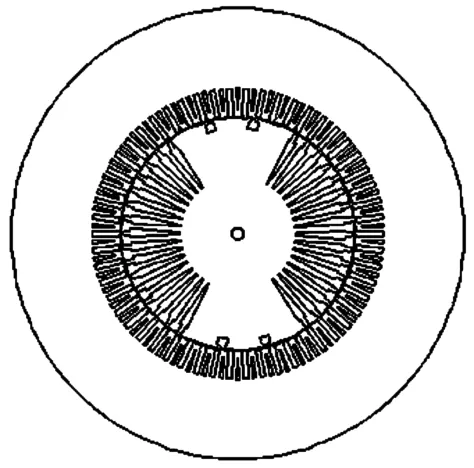
图2 7.5 kW模型机结构示意图Fig.2 Structure of a 7.5 kW prototype

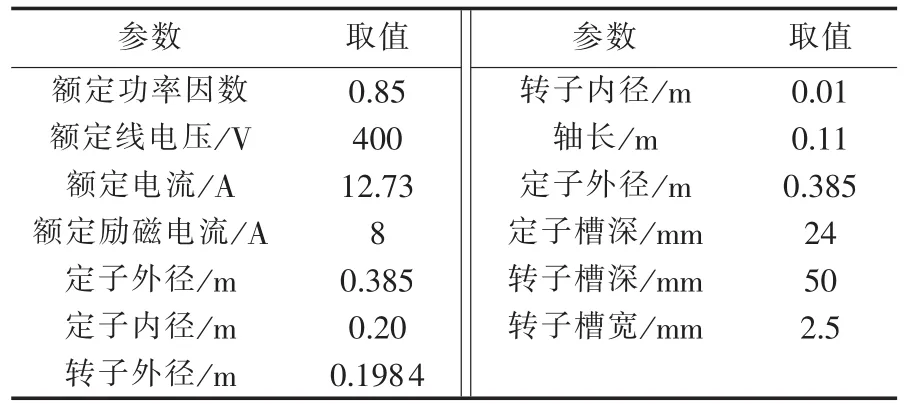
表1 7.5 kW模型机基本结构数据Tab.1 Structural data of a 7.5 kW prototype

2.2 不同方法所计算瞬态时间常数的对比分析

采用时步有限元、改进解析表达式和传统解析表达式计算7.5 kW电机端电压为110 V时突然三相短路后的励磁电流，结果如图3所示。7.5 kW电机的参数通过试验测得，如表2所示，表中数据均为标幺值。时步有限元不计及阻尼作用。

根据改进解析表达式和传统解析表达式，计算出空载三相突然短路励磁电流见式（18）和（19）。

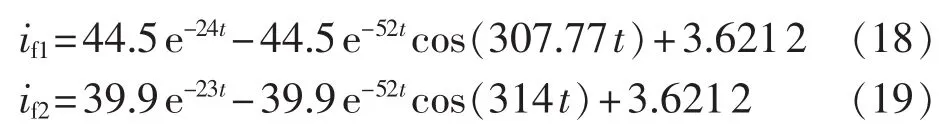
从上述两式可以得出瞬态时间常数的改进解析解和传统解析解，如表3所示，表中τ′d为直轴瞬态时间常数，τa为定子非周期衰减时间常数。而从时步有限元计算的励磁电流中无法直接获得瞬态时间常数的大小，因此本文采用Prony方法[15-17]对时步有限元计算的励磁电流曲线进行拟合，从而得出直轴瞬态时间常数和定子非周期衰减时间常数的数值。

对比图3中的励磁电流曲线和表3中的瞬态时间常数，得出改进解析表达式计算的励磁电流曲线和瞬态时间常数与时步有限元结果更加接近，而传统解析解与时步有限元相差较大。

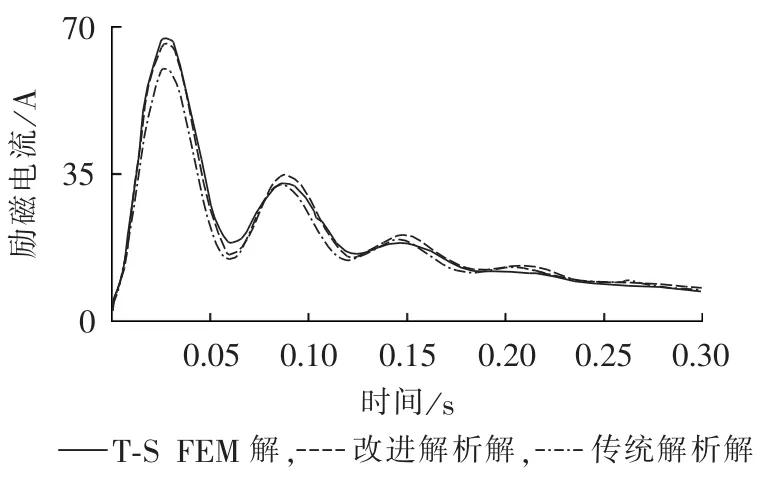
图3 不同方法得到的励磁电流对比Fig.3 Comparison of excitation current among different methods

表2 3种不同功率同步电机的参数对比Tab.2 Comparison of synchronous machine parameters among three capacities

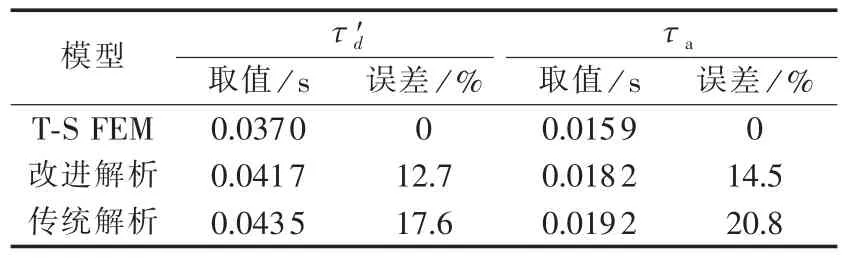
表3 不同方法得到的瞬态时间常数对比Tab.3 Comparison of transient time constant among different methods

2.3 定转子电阻对瞬态时间常数的影响

为研究定转子电阻对瞬态时间常数的影响，在7.5 kW电机定子三相绕组出线端串入阻值4.286 Ω的电阻，进行时步有限元仿真并与改进解析解和传统解析解对比，得到励磁电流响应曲线对比见图4。

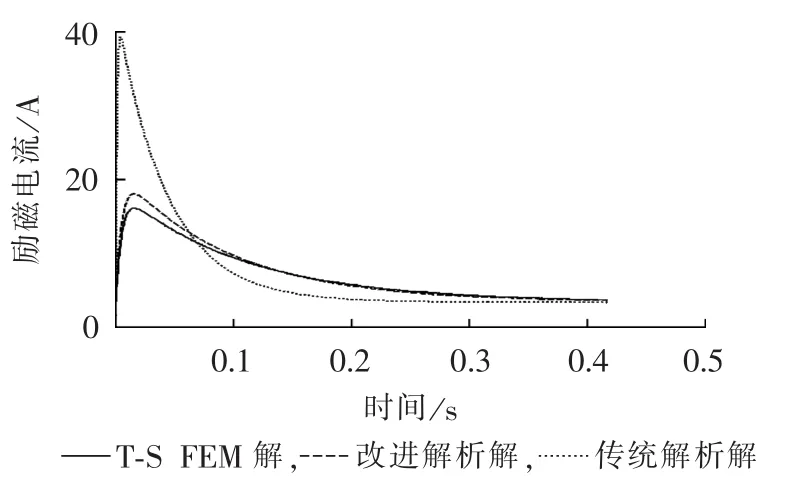
图4 定子串电阻后的励磁电流曲线Fig.4 Excitation current when a serial resistor is added to stator winding

从图4可知，改进解析表达式计算的励磁电流曲线与时步有限元结果更接近。对时步有限元的励磁电流曲线进行Prony拟合，得到直轴瞬态时间常数与改进解析解一致，约0.12 s，而传统表达式计算的直轴瞬态时间常数不随定子电阻变化，仍然为表3的0.0435 s。因此说明定子电阻变化会影响直轴瞬态时间常数大小，而传统解析表达式不能计及该影响。

令定、转子电阻在实际值的10%到实际值的10倍范围内变化，采用改进解析表达式计算出7.5 kW同步电机2个瞬态时间常数的数值。对计算结果进行总结和分析发现，直轴瞬态时间常数随着定子电阻的增大而增大，随着转子电阻的增大而减小，如图5所示。

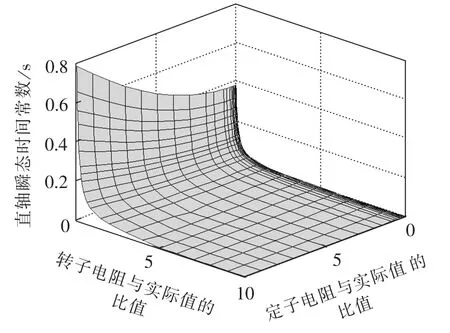
图5 直轴瞬态时间常数随定转子电阻的变化规律Fig.5τ′dvs.stator and rotor resistances

同样，在转子绕组中串入12.7 Ω电阻后，采用时步有限元、改进解析表达式和传统解析表达式计算的励磁电流曲线如图6所示。对时步有限元计算的励磁电流曲线进行Prony拟合，得出定子非周期时间常数与改进解基本一致，约为0.023 s，而传统表达式计算的定子非周期时间常数不随转子电阻的变化而变化，仍为表3所示的0.0192 s。因次说明转子电阻的变化会影响定子非周期时间常数的大小，而传统解析表达式不能计及这种影响。

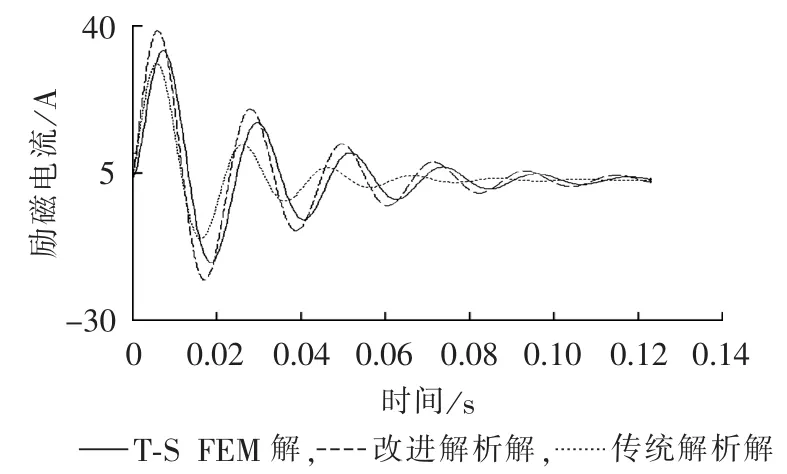
图6 转子串电阻后的励磁电流Fig.6 Excitation current when a serial resistor is added to rotor winding

令定、转子电阻在实际值的10%到实际值的10倍范围内变化，采用改进解析表达式计算出定子非周期衰减时间常数随定转子电阻的变化规律如图7所示，得出定子非周期衰减时间常数随着转子电阻的增大而增大，随着定子电阻的增大而减小。

2.4 瞬态时间常数改进解相对于传统解的偏差分析

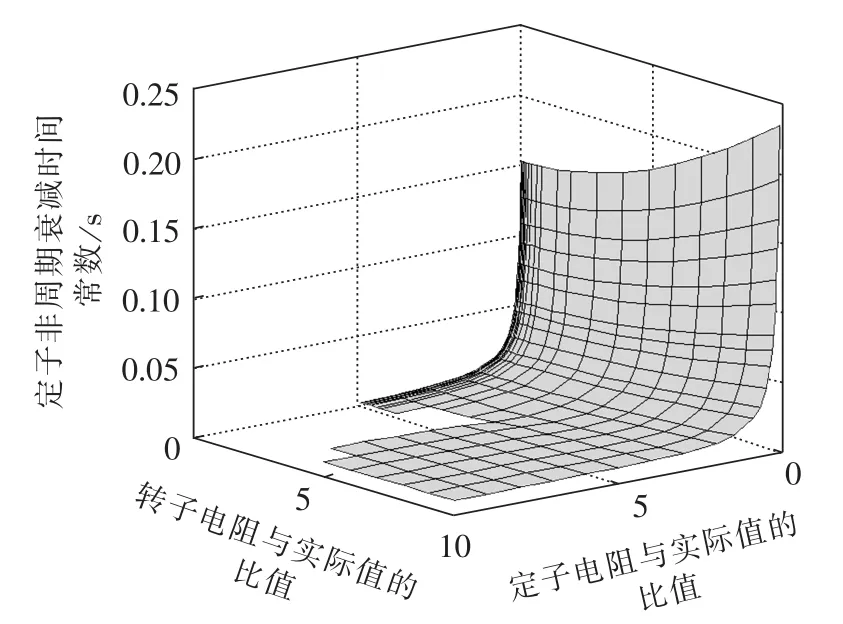
图7 定子非周期衰减时间常数随定转子电阻的变化规律Fig.7τavs.stator and rotor resistances

从表2可知不同功率同步电机的定转子电阻标幺值相差近10倍。为分析不同定转子电阻值情况下，瞬态时间常数改进解与传统解的差别，将7.5 kW同步电机定转子电阻在实际值的10%至实际值的10倍范围内变化，计算不同定转子组合时直轴瞬态时间常数和定子非周期衰减时间常数的改进解相对传统解的偏差。改进解相对传统解的偏差α和β为：

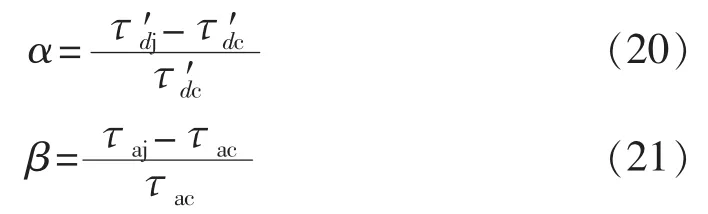
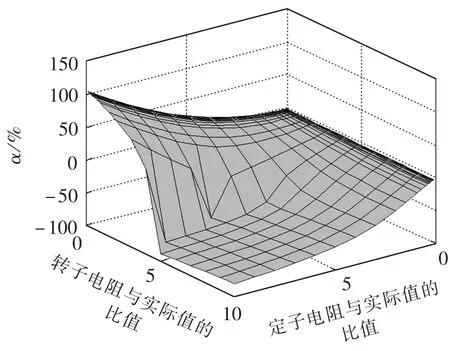
图8 不同定转子电阻时τ′dj相对于τ′dc的偏差Fig.8 Error ofτ′djrelative toτ′dcfor different stator and rotor resistances

图9 不同定转子电阻时τaj相对于τac的偏差Fig.9 Error ofτajrelative toτacfor different stator and rotor resistances

从图8中可以看出，随着定子电阻的增大，α的绝对值在不断增大。实际电阻下，α值为2.5%，当定子电阻增大到10倍，α变为53%。同样，从图9中可以看出，实际电阻下，β值为0.6%，10倍的定、转子电阻下，β变为181%。可见，对于小功率电机而言，瞬态时间常数的传统解与改进解具有很大差别。

采用上述方法计算不同定转子电阻时，300 MW同步电机瞬态时间常数改进解相对于传统解的偏差。结果发现，在相同定转子电阻变化范围内，直轴瞬态时间常数的改进解相对于传统解的最大偏差为0.13%，而定子非周期衰减时间常数的改进解相对于传统解的最大偏差仅为0.09%。因此，瞬态时间常数的改进解对于大型发电机并无明显精度优势。