空穴掺杂及温度对CrSi2热电特性的影响
2014-09-26吴瑞峰
吴瑞峰
(郑州旅游职业学院机电工程系,河南 郑州 450009)
空穴掺杂及温度对CrSi2热电特性的影响
吴瑞峰
(郑州旅游职业学院机电工程系,河南 郑州 450009)
采用基于第一性原理的密度泛函理论对CrSi2的能带结构、态密度进行了理论计算,基于半经典玻尔兹曼理论的BoltzTrap程序计算了p型或n型掺杂条件下载流子范围对CrSi2的热电特性的影响.结果表明,z轴方向上的输运特性高于其他方向,p型掺杂CrSi2的热电特性优于n型掺杂的热电特性.较大ZeT值出现温度为1 500 K时的p型掺杂,这时载流子单位体积范围为4.578×1020~7.873×1020cm-3,这刚好落在最佳的热电特性所对应的载流子范围(1019~1021cm-3)内.
CrSi2;能带结构;热电特性
开发新能源并通过降低能耗等方式是解决当前能源危机问题的重要途径.全球约超过一半的能源消耗都以热能的形式散失,倘若对一小部分的能量加以回收利用,这将对全球的节能降耗产生深远影响,由此诞生了一项新的能源材料——热电材料.它能够利用废热重新获得能量或同时发热发电,从而避免了对大气造成污染[1,2].CrSi2化合物具有C40的六方晶体结构,由于便宜、无毒、由单位体积含量丰富的元素组成,故作为一种潜在的性能较好的热电材料已受到科研人员的高度重视和广泛研究[3~5],有望作为中、高温热电材料得到实际应用.但是,由于传统的CrSi2量纲一优值ZT值比较低,研究人员通过掺杂来改变载流子的范围,从而来控制塞贝克系数和高的电导率[6,7].此外,PARKER 等[3]研究发现,高温条件下CrSi2的热电优值可通过1×1021~4×1021cm-3范围的电子掺杂来提高,但对于空穴掺杂没有研究.目前,国内外有关CrSi2电子结构的理论研究较多[3~7],但涉及其热电特性方面的理论研究却非常少.鉴于此,本研究采用第一性原理对CrSi2的能带结构和态密度进行了计算,并基于半经典玻尔兹曼理论的基础,用Boltztrap程序完成了输运性质的计算.以求在更大范围内找出热电优值更高的热电材料.
1 CrSi2的理论模型和计算方法
1.1理论模型
本研究选用具有六角形C40结构的CrSi2作为计算模型, 它属于P 6222 的空间群, 晶格常数为a=b=4.426 8×10-10m,c=6.368×10-10m,晶面角α=β=90°,γ=120°;图1给出了CrSi2晶胞的结构,每个晶胞中包含6个硅原子和3个铬原子.为了显示CrSi2在倒空间的各向异性的一维结构,图2给出了它的第1布里渊区结构.
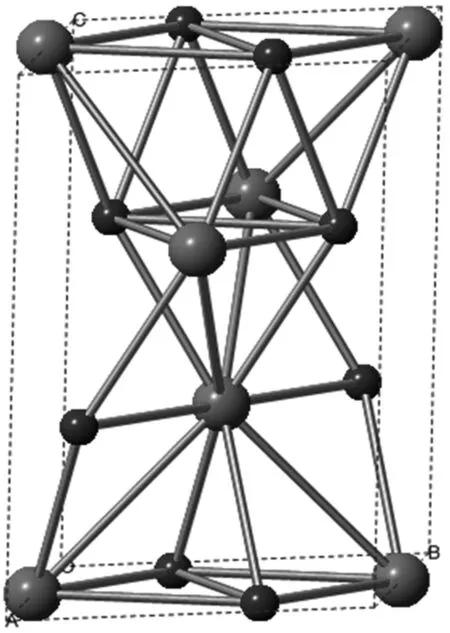
小球代表Cr原子,大球代表Si原子Small and large spheres represent Cr and Si atoms, respectively.
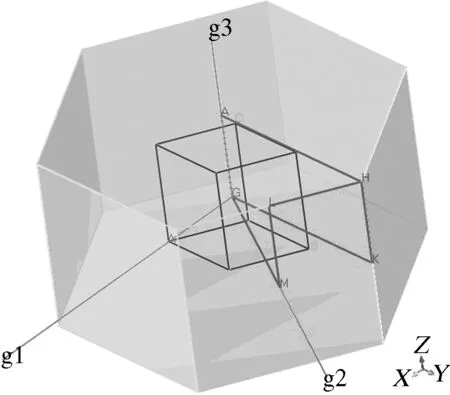
图2 CrSi2的第1布里渊区Fig.2 The first Brillouin zone of CrSi2
1.2模拟方法
用基于密度泛函理论的线性投影缀加平面波方法对CrSi2的初始结构进行了优化[8].经过多次试算,确定平面波截断能为500 eV(3次优化用得K点分别选为9×9×5 , 13×13×8 ,17×17×10),当2次迭代的总能量差小于10-5eV时,能量优化结束.在优化的CrSi2的晶格结构基础上,利用基于密度泛函理论的全势缀加平面波方法计算了CrSi2的电子结构.在自恰计算中,把第1布里渊区用于电子计算的K点设为1 000,当2次迭代的总能量差小于0.001 36 eV ,自恰收敛.在计算中考虑了标量相对论,但由于Si和Cr原子都是轻原子,因此,在计算时没有考虑自旋轨道耦合.
在计算的电子结构基础上,用半经典玻尔兹曼理论计算材料的输运性质,这个计算由BoltzTrap程序完成.在计算过程中弛豫时间作为常数处理,采用刚性带模型来模拟掺杂单位体积含量的变化,在这个模型里面,假定在能隙附近的能带结构不随掺杂的种类和数目变化,载流子单位体积含量的变化仅仅引起化学势位置的变化,载流子单位体积含量越高,费米能越远离带边,通常这种方法要求掺杂的单位体积含量不能太高.这种计算方法已被用于分析多种化合物的热电优值和掺杂单位体积含量,并且得到了和试验较为吻合的结果[9].
2 CrSi2的能带结构和态密度
依据优化后的晶体结构,计算了本征CrSi2晶体的能带结构、总体态密度和部分态密度,计算结果如图3和图4所示.图3中的虚线代表费米能级, 从图3 中可以看出, CrSi2的费米面偏向其价带,因此,CrSi2为p型半导体,空穴载流子控制其热电传输性能,在点M和点L之间存在一值为0.358 eV的间接能隙,与其他理论计算值(0.3~0.35 eV)符合得很好[5],表明本理论计算的结果是可靠的.较窄的带隙让电子跃迁变得更加容易,从而有利于改善热电材料的热电性能.
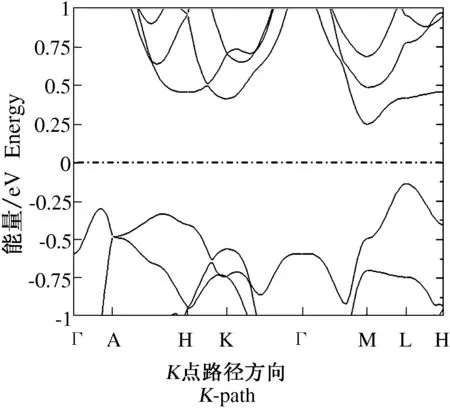
图3 CrSi2的能带结构 Fig.3 Calculated band structures of CrSi2
能带结构计算在预测热电性能方面已被证明是一种十分有用的工具.从图3可以看出,在A和H之间的导带非常平缓,以及K与Γ之间相对较平缓的导带,其弥散少于0.2 eV.从带边可看出,在较大区域内,价带与导带的动量空间都少于0.5 eV.ab-平面内的一个六角单胞的晶格常数为4.426 8×10-10m,c轴晶格常数为6.368×10-10m,使得能带质量很大.对于金属和简并半导体来说,能带质量和塞贝克系数S的关系可表示为:
(1)
式中:n是载流子单位体积含量,m*是能带有效质量,kB是玻尔兹曼常数.
由式(1)可知,能带质量m*和塞贝克系数S呈正比.因此,CrSi2借助其显著的重带性质而表现出其优良的热电特性.
因为费米面附近的电子态对热电性质有重要影响,计算了CrSi2总的态密度( DOS)和分态密度( PDOS)图,对本体CrSi2中Cr原子和Si原子的核外各层电子对能带和态密度各部分的贡献进行分析.从图4可以看出,在-15~-4 eV 范围内,CrSi2的能态密度曲线主要由Si的3s和3p态电子构成;在-4~0 eV 范围内,主要是由Cr的3d态电子和Si的3p态电子构成;在0~5 eV范围内,主要由Cr的3d态电子和Si的3p态电子构成且Cr的3d态电子处于支配地位.在5 eV以上范围的态密度曲线,又主要是由Si的3p态电子构成.
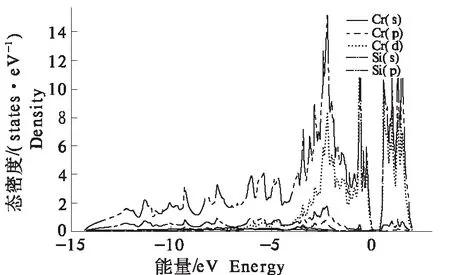
图4 CrSi2的态密度图Fig.4 Calculated DOS of CrSi2
综合起来看,在费米面附近,CrSi2的能态密度主要是由Cr的3d和Si的 3p态电子的能态密度确定,也即价带顶部和导带底部的能带均主要是来源于Cr的3d电子和Si的3p电子的贡献.因此,本征CrSi2的电传输性质及载流子类型主要由Cr的3d态电子和Si的3p态电子决定.这与PARKER等[3]的结果一致.
3 空穴掺杂及温度对CrSi2热电特性的影响
通常情况下,CrSi2形成一种简并的p型半导体,最近又研发了它的n型样本.因此,研究了p型或n型掺杂下载流子单位体积含量的变化对热电特性的影响.考虑到CrSi2各向异性的一维结构,分别研究了材料在x,y和z方向上的输运特性,计算得到的S,σ/τ,S2σ/τ和ZeT随温度变化的曲线分别在图5展示,其中电子热导率在决定热电优值方面扮演着重要的角色,把ZeT=S2σT/κe叫做CrSi2的最大电子热电优值[11].这些输运特性分别是在温度为300, 900, 1 200和1 500 K时的条件下计算的.这个输运性质计算是在载流子单位体积含量在-3×1021~3×1021cm-3的范围内给出的,计算过程没有考虑掺杂类型.
由计算结果可知,CrSi2在x和y轴方向的输运特性是相同的,而在z轴方向的输运特性比在x和y轴方向上好.图5-a给出了σ/τ(电导率相对于弛豫时间)随载流子单位体积含量的变化.从图5-a中可以看出,σ/τ的各向异性受载流子单位体积含量的变化影响较大,而受温度的影响较小.不论p型掺杂或是n型掺杂,σ/τ都随着载流子单位体积含量的增加而增加.电导率σ与载流子单位体积含量n和迁移率μ有如下关系:
σ=neμ
(2)
因此,图5-a和式(2)给出的电导率和载流子单位体积含量呈正比的关系是一致的.
对于p型掺杂,σ/τ的各向异性随载流子单位体积含量的增加而增加,并相对于n型掺杂来说,σ/τ的各向异性比较大,n型掺杂时σ/τ的x轴方向要比z轴方向略大,而p型掺杂z轴方向σ/τ值远大于x轴方向的σ/τ值,而总体来看,p型掺杂得到的z轴方向σ/τ值比较大.
图5-b给出了S(塞贝克系数)的各向异性随载流子单位体积含量的变化,和σ/τ的各向异性不同,S的各向异性较小.但是S随载流子单位体积含量n的增大而减小,这因为根据式(1)可知,对于简并半导体中S和n是呈反比的.
图5-c给出了S2σ/τ(功率因子)随载流子单位体积含量的变化关系.从图5-c明显可以看出,对于S2σ/τ来说,p型掺杂的各向异性大于n型掺杂的各向异性,并且S2σ/τ的各向异性主要来源于σ/τ的各向异性.在1 500 K时5.935×1020cm-3的空穴掺杂中,z轴方向出现高达15.704×1011W·K-2·ms-1的S2σ/τ,这是传统热电材料PbTe的S2σ/τ的3倍.
如图5-d所示,在同一温度下,随着载流子单位体积含量的增加,ZeT先增加后减小,p型掺杂的ZeT峰值高于n型掺杂的.其中较大ZeT值出现的载流子范围4.578×1020cm-3到7.873×1020cm-3,这个单位体积含量刚好落在最佳的热电特性所对应的载流子范围(1019~1020cm-3).
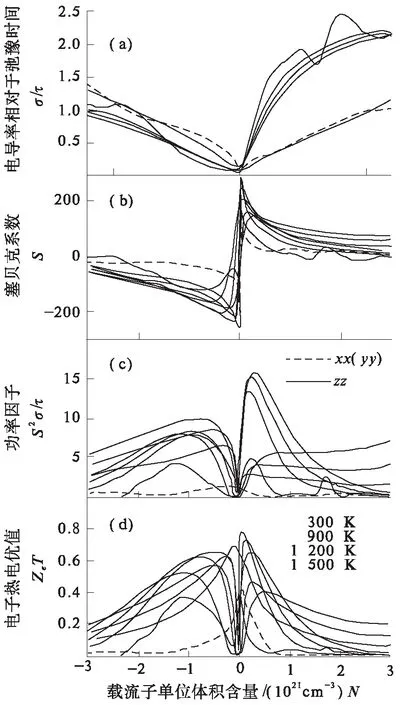
(a)电导率相对于弛豫时间(σ/τ( 1020Ω-1·ms-1); (b)塞贝克系数[S/(10-6V·K-1)]; (c)功率因子相对于弛豫时间(S2σ/τ)/ (1011W·K-2·ms-1); (d)ZeT.
(a)Electrical conductivities relative to relaxation time,σ/τ(1020Ω-1·ms-1); (b)Seebeck coefficients,S(10-6V·K-1); (c)power factor with respect to relaxation time,S2σ/τ(1011W·K-2·ms-1).(d)ZeT.
图5CrSi2在x,y和z轴方向上的输运特性和载流子单位体积含量的关系
Fig.5CalculatedtransportcoefficientsofCrSi2asfunctionofcarrierconcentration
4 结论
应用第1性原理的计算方法和玻尔兹曼理论计算了本证CrSi2的电子结构并预测了p型或n型掺杂下载流子单位体积含量的变化对热电特性的影响.研究发现,p型掺杂CrSi2的热电特性优于n型掺杂的热电特性,在1 500 K 时5.935×1020cm-3的空穴掺杂中,z轴方向出现高达15.704 1×1011W·K-2·ms-1的S2σ/τ,这是传统热电材料PbTe的S2σ/τ的3倍.而较大ZeT值出现温度为1 500 K时的p型掺杂的z轴,这时载流子范围从4.578×1020cm-3到7.87×1020cm-3.CrSi2各向异性的输运性质和CrSi2各向异性的一维晶格结构密切相关.改变载流子单位体积含量的大小不但能改变ZeT峰值的大小,同时也改变了出现这个峰值所对应的温度大小.此外,若能将不同掺杂单位体积含量下的CrSi2分段连接起来,组成复合型的材料,并且使每一段都处在能产生较大ZT值的温度范围,就有可能使CrSi2在较宽温度范围内达到最大的热电转换效率.
[1] CRONIN B. Vining.An inconvenient truth about thermoelectrics[J] .Nature Materials, 2009,8(2):83-85.
[2] MAHAN G, SALES B, SHARP J.Thermoelectric materials: new approaches to an old problem[J]. Physics Today, 2008, 50(3): 42-47.
[3] Parker D, SINGH D J.Very heavily electron-doped CrSi2as a high performance high temperature thermoelectric material [J]. New J Phys, 2012, 14 (3):33045-33055.
[4] UDONO H, KIKUMA I, OKUNO T, et al. Optical properties of β-FeSi2single crystals grown from solutions[J]. Thin Solid Films, 2004, 461(1): 182-187.
[5] 周士芸,谢 泉,陈 茜. CrSi2电子结构及光学性质的第一性原理计算[J].中国科学:G辑,2009,39(2):175-180.
[6] PAN Z J, ZHANG L T, WU J S. Effects of Al doping on the transport performances of CrSi2single crystals[J].Scripta Materialia, 2007, 56(3) :245-248 .
[7] PAN Z J, ZHANG L T, WU J S. Effects of V doping on the transport performances of CrSi2single crystals[J].Scripta Materialia, 2007,56(3) :257-260 .
[8] KRESSE G, HAFNER J. Ab initio molecular dynamics for liquid metals[J]. Phys Rev B, 1993,47 (4):558-562.
[9] YAN Y L, WANG Y X, ZHANG G B. Electronic structure and thermoelectric performance of zintl compound Ca5Ga2As6[J] .Journal of Materials Chemistry, 2012, 22 (1): 20284-20290.
(责任编辑:常思敏)
EffectofholedopantandtemperatureonthermoelectricpropertyofCrSi2
WU Rui-feng
(Department of Electromechanic, Zhengzhou Tourism College, Zhengzhou 450009, China)
The energy band structures and density of states of intrinsic CrSi2have been calculated using the first-principles pseudo- potential method based on the density funct ional theory (DFT). The transports coefficients correspond to p-and n-type doping are derived from the electronic structure by using the semiclassical Boltzmann theory as implemented in the BoltzTrap code. The result shows that transport coefficients along thezaxis should be significantly larger than those for the others,and the transport properties of p-type CrSi2could be better than that of n-type.A high ZeT of CrSi2could be achieved by hole doping with concentration range of 4.578×1020cm-3to 7.873×1020cm-3at 1 500 K,which lies exactly in the corresponding range from 1019to 1021cm-3of the optimum thermoelectronic property.
CrSi2; band structure;thermoelectric property
TQ 511
:A
2014-04-03
国家自然科学基金资助项目(11102060)
吴瑞峰,1968年生,男,河南鹤壁人,副教授,硕士,主要从事热电材料研究.
1000-2340(2014)05-0619-04
