赣江二桥主桥地震反应分析
2014-09-26王毅
王 毅
(上海市政工程设计研究总院(集团)有限公司,上海市 200092)
0 引言
随着我国国民经济及交通建设的快速发展,斜拉桥因其造型美观、造价经济、施工工艺成熟等特点广泛适用于中等以上跨径的桥梁。近年来,钢混组合斜拉桥由于充分利用混凝土及钢材的受力特性,在桥梁建设中得到日益广泛的应用。然而,我国现行桥梁抗震设计规范仅适用于中等跨径的普通桥梁,没有适用于斜拉桥及钢混组合结构桥梁的专用规范。
本文以赣江二桥主桥为对象,用反应谱法对不同常数阻尼比下的计算结果进行比较,并结合采用Rayleigh阻尼比的时程分析结果,说明结构阻尼比对结构地震反应的影响程度,提出用应变能比例法计算结构阻尼及用时程分析法校核结构动力分析,为类似的钢混组合斜拉桥抗震分析提供参考。
1 概述
赣江二桥是吉水县城跨越赣江的一座特大城市桥梁,全长约1 310 m,分为跨赣江主航道主桥、西引桥和东引桥三部分。主桥为独塔双索面预应力混凝土梁斜拉桥,桥跨布置为110 m+110 m,全桥长220 m,标准桥宽36 m,双向4车道加非机动车道和人行道,设计车速60 km/h。
主桥采用塔梁固结、边墩纵向滑动的结构体系,主梁为双主梁预应力混凝土结构,主塔为钢混组合结构,塔高90 m,沿塔高分为承台以上0~39.5 m混凝土塔柱、39.5~44.2 m钢混结合段塔柱及44.2~90 m钢结构塔柱三个区段。斜拉索采用扇形平行索面布置,主塔两侧各17对索。主塔承台为哑铃型,采用直径2.5 m的钻孔灌注桩。主桥立面布置见图1所示、主塔横立面及侧力面分别见图2、图3所示。
2 抗震设防水准及设防性能目标
现行《城市桥梁抗震设计规范》(CJJ 166-2011)采用两水准设防、两阶段设计的抗震设计思想进行桥梁抗震设计。根据抗震设防分类标准,赣江二桥主桥为甲类桥梁,结合结构构件的受力特点、重要性、震后抢修难易度及震后确保使用功能等原则对不同水准地震作用下各结构部位抗震设防性能目标如表1所列。
3 有限元模型和动力特性分析
3.1 有限元模型
采用通用有限元分析软件Midas Civil 2010建立主桥的三维有限元模型(见图4)。主塔、边墩、桩及承台均采用空间梁单元模拟,拉索采用桁架单元模拟。为准确模拟主梁的抗扭刚度,桥面系采用空间梁格模拟。边界连接条件为:塔梁固结;边墩与主梁纵向可滑动,横向主从约束。主塔为高桩承台基础,动力分析模型中桩基采用等效嵌固模型模拟桩-土相互作用。
3.2 动力特性分析
分析和把握桥梁的动力特性是进行抗震性能分析的基础,以全桥的成桥状态为初始条件,对计算模型采用子空间迭代法进行桥梁结构动力特性分析,主桥的前10阶自振频率及振型特征如表2所列。
4 主桥抗震性能分析
4.1 抗震概念设计
桥梁的抗震概念设计包括正确的场地选择、合理的桥型布置、理想的结构体系选择等。

图1 主桥立面布置图(单位:m)
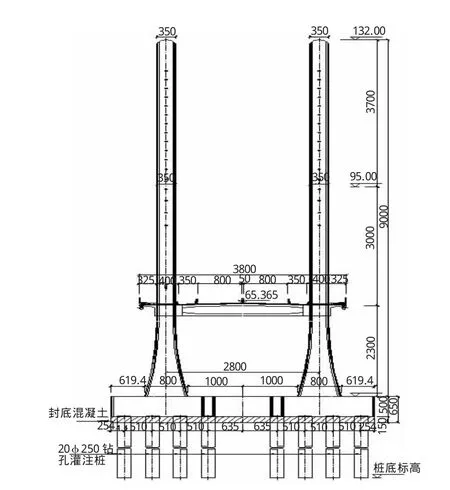
图2 主塔横立面(单位:m)
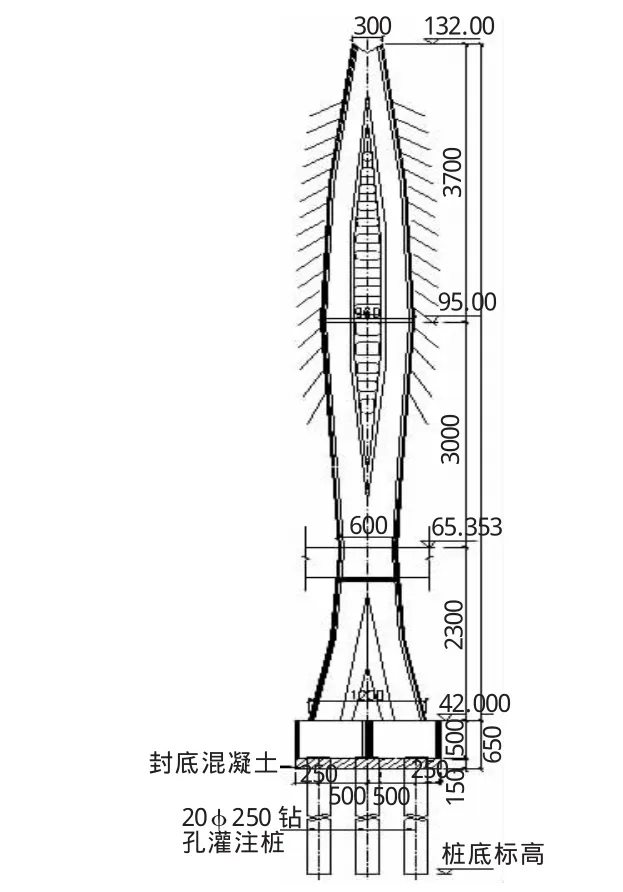
图3 主塔侧立面(单位:m)
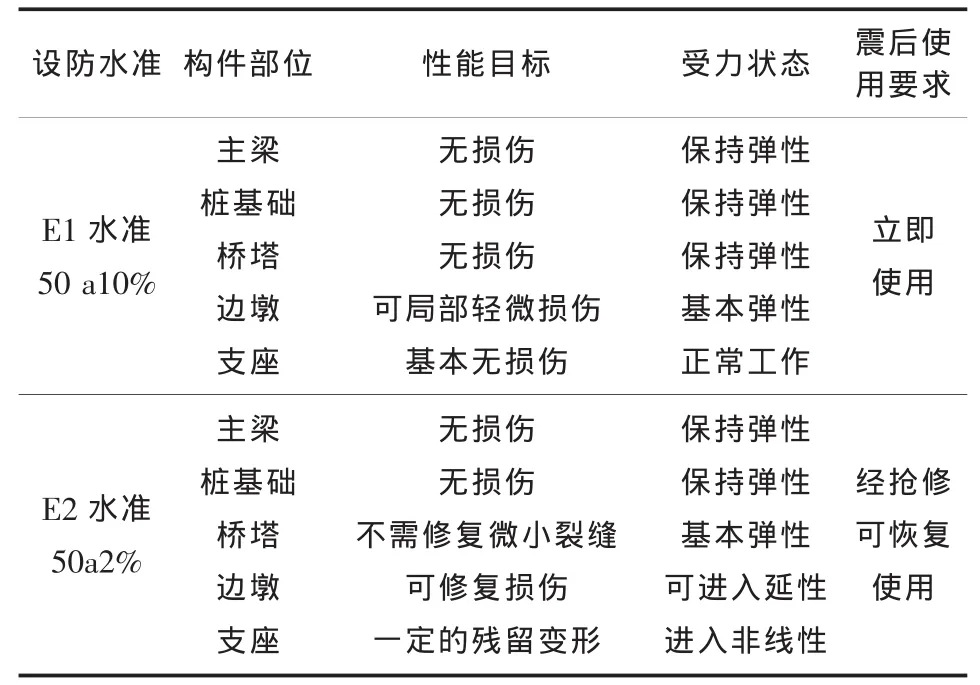
表1 抗震设防性能目标一览表
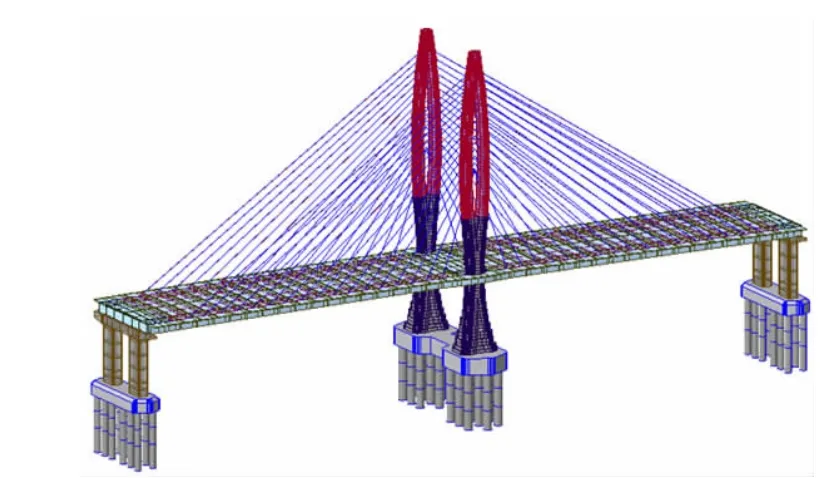
图4 主桥动力分析模型
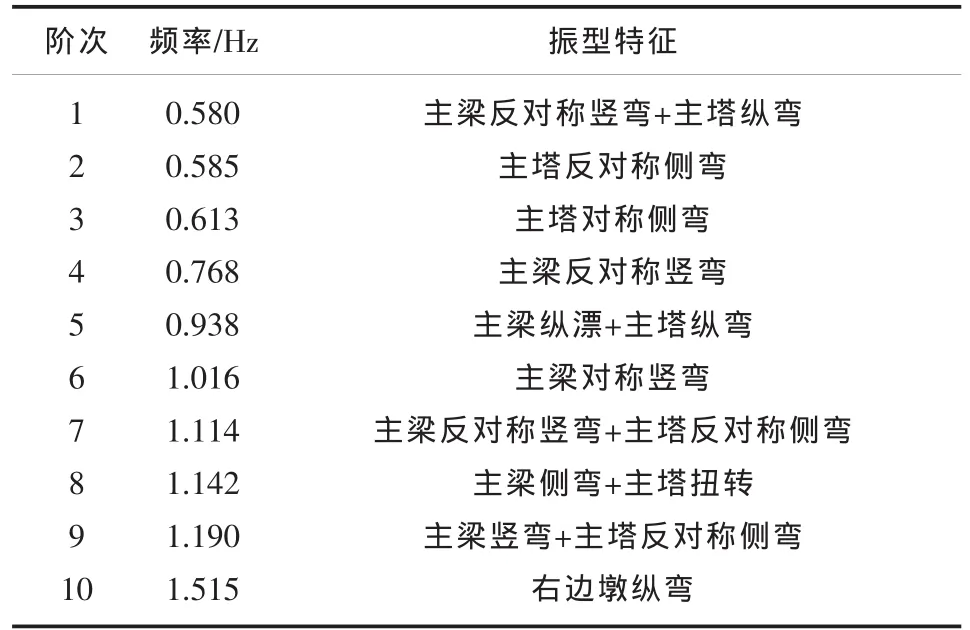
表2 主桥动力特性一览表
斜拉桥的结构体系主要分为纵向全漂浮或半漂浮、塔梁固结、塔梁纵向弹性约束、纵向阻尼约束体系四类。经过对各种结构体系综合分析比较,结论为:
(1)塔梁固结体系水平位移小,有效地改善双塔柱在静、动力荷载作用下的协同性,塔梁结合部的构造简单,施工阶段无需临时固结装置,方便施工。主塔及基础设计由地震控制。
(2)全漂浮体系结构动力响应小,但水平位移大,且对主梁抗扭不利。
(3)索塔处设竖向支座对结构总体刚度和静力反应影响不大,仅影响支座处主梁局部受力。
(4)塔梁弹性约束体系能减小结构在静、动力荷载作用下的水平位移,但在构造上存在困难,同时无法改善双塔柱的协同工作。
结合主桥横断面布置,全漂浮体系和半漂浮体系均需主梁在塔柱处开孔,构造复杂,传力路径不直接。
综合考虑结构在汽车活载、风荷载、温度作用和地震作用等多种组合工况下的强度、刚度和稳定性,结构采用塔梁固结体系,在边墩上设置纵向滑动支座。
4.2 地震反应分析
4.2.1 地震输入
地震输入取自《吉水赣江二桥工程场地地震安全性评价报告》(以下简称《报告》)。《报告》提交桥址场地水平向地表设计峰值加速度为:50 a10%超越概率为0.056 g;50 a2%超越概率为0.118 g。图5、图6分别为50 a超越概率2%的水平地震加速度反应谱和水平地震加速度时程(波1)。

图5 水平地震加速度反应谱(阻尼比5%)曲线图
4.2.2 地震反应分析
赣江二桥主桥的地震反应分析采用反应谱法和时程分析法2种方法进行,以相互校核。地震输入方式为:(1)纵向;(2)横向。反应谱分析取前350阶振型,振型组合方式采用CQC法,地震作用效应组合方式采用SRSS法。
图6 水平地震加速度时程图示(阻尼比5%)
现行桥梁抗震设计规范中明确了钢斜拉桥、混凝土斜拉桥的阻尼比,通常采用常数阻尼比即所有振型均采用相同的阻尼比进行结构抗震分析。该桥主塔为钢混组合结构,为比较不同结构阻尼比对地震响应的影响,分别按阻尼比0.03、0.05进行反应谱分析(以下简称反应谱1、反应谱2)。
采用线性时程分析方法对主桥进行地震反应分析时,主塔钢结构的阻尼比取0.02,钢筋混凝土结构阻尼比取0.05,斜拉索取0.01,根据应变能法计算不同材料组成的结构体系的等效振型阻尼比,结构阻尼比根据参考振型确定瑞利阻尼。时程分析结果采用3组地震波响应的最大值。
反应谱分析及时程分析的结果见表3、表4所列。
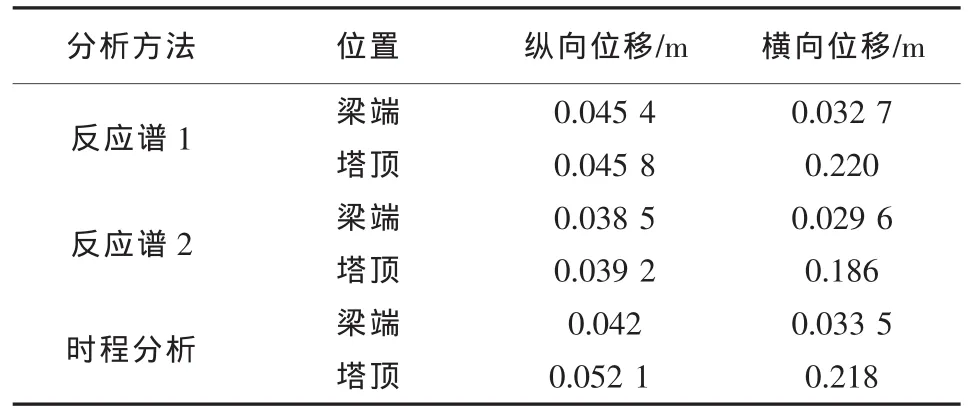
表3 主桥各控制位置处最大地震位移(50 a2%)一览表

表4 主塔各控制截面处弯矩 (50a2%)一览表
从表3、表4可以看出,阻尼比越小地震响应越大。当整体结构阻尼比分别取0.03和0.05时,最大地震位移和主塔控制截面内力响应相差8%~18%。
对于主塔在地震作用下尚处于弹性状态,反应谱1的计算结果除塔顶横向位移与时程分析结果相差12%以上,其余结构构件的内力及变形响应的差值均在5%以内,计算精度满足设计要求。
4.2.3 抗震验算
限于篇幅,仅列出主塔的抗弯强度验算结果。在进行E1地震作用阶段抗弯强度验算时,截面的抗弯强度取截面的初始屈服弯矩,即要求结构在E1地震作用阶段处于弹性范围内工作。进行E2地震作用阶段抗弯强度验算时,截面的抗弯强度取截面的等效屈服弯矩,即验算结构在E2地震作用阶段是否进入塑性。
如表5所列,反应谱分析及抗震检算结果表明,在E1、E2地震作用下,主塔控制截面尚处于弹性状态满足抗震设防性能目标。
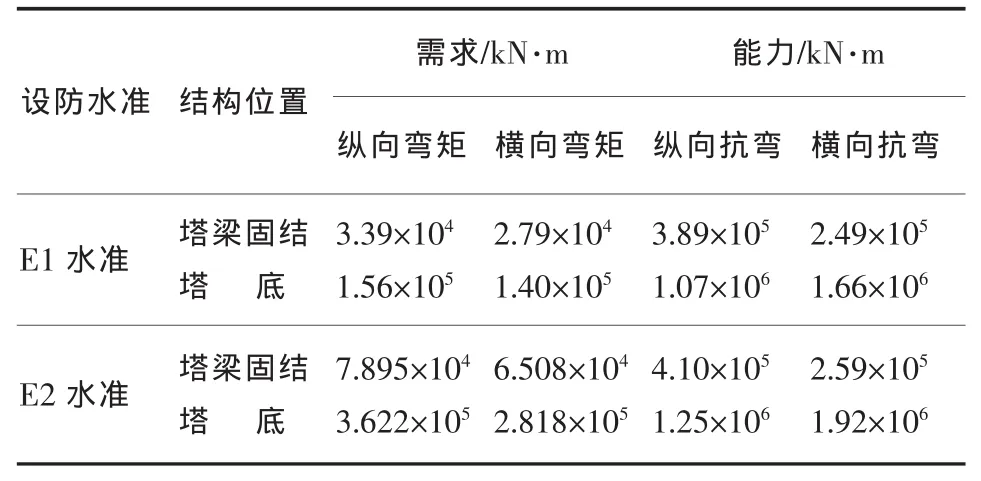
表5 主塔各控制截面处抗弯能力检算一览表
5 结论
(1)阻尼比选取的合适与否对钢混组合斜拉桥的地震响应产生显著影响。
(2)钢混组合斜拉桥需根据钢结构在整体结构中所占比重,合理确定其阻尼比,采用反应谱法和时程分析法进行相互校核。
(3)该桥主塔控制截面在强震后尚处于弹性状态,采用较低阻尼比进行反映谱分析的结果与线性时程分析结果较为一致。
(4)对于强震后结构进入弹塑性状态,结构阻尼比将显著增加,对此类桥梁需另作具体研究而定。
[1]CJJ 166-2011,城市桥梁抗震设计规范[S].
[2]JTG/T B02-01-2008,公路桥梁抗震设计细则[S].
[3]江西省防震减灾工程研究所.吉水县赣江二桥工程场地地震安全性评价报告[R].2012.
[4]范立础.桥梁抗震[M].上海:同济大学出版社,1997.
[5]叶爱君,胡世德,范立础.斜拉桥抗震结构体系研究[J].桥梁建设,2002,(4).
[6]胡聿贤.地震工程学(第二版)[M].北京:地震出版社,2006.
