一种低纹波输出非标准正弦电流有效值转换电路

孟彦京，李林涛，高筱筱，谢仕宏

(陕西科技大学电气与信息工程学院，西安710021)

一种低纹波输出非标准正弦电流有效值转换电路

孟彦京*，李林涛，高筱筱，谢仕宏

(陕西科技大学电气与信息工程学院，西安710021)

首先介绍了目前用于电流有效值转换的方法，分析了每种方法的特点，并以AD637芯片为核心搭建了典型应用电路，通过输入方波信号，发现其输出纹波含量较高，输出结果含有较大误差。在AD637典型应用电路的基础上搭建了基于Sallen-Key滤波电路的非标准正弦电流有效值转换电路，并通过优化滤波电路的参数，使得输出纹波含量降低为典型应用电路的10%以下，提高了非标准正弦电流信号有效值转换的精度。

电子电路;低纹波;Sallen-Key滤波;电流检测;非标准正弦信号;有效值;AD637

常见的电流有效值转换方法有热转换法，峰值法，平均电流法，数学定义法等［1-3］，AD637芯片采用基于有效值数学定义隐式计算的方法，在非正弦电流信号的有效值转换方面有着动态范围较大、所需电路元器件较少、成本低廉的优势。

目前国内也有用基于AD637而搭建的有效值转换电路［2，4］，但是其输出纹波含量高，缺乏对相关电路参数的分析、计算。

本文在AD637典型应用电路的基础上搭建了基于Sallen-Key滤波电路的非正弦电流有效值转换电路，并且通过分析、计算，优化了滤波电路的参数，使得输出纹波比典型应用电路大大降低，提高了非正弦电流信号有效值转换的精度。

1 有效值的计算方法

1.1 热转换法

理论上，热转换［2］是最简单的方法，但实际上它却是最难以实现、成本最高的方法。这种方法是将未知交流信号的热值与已知直流基准电压的热值进行比较。由于温度这一物理量具有较大的时滞性，因此解决热转换器的动态范围限制问题，会使得转换器变得异常复杂，并且使成本急剧增高。

1.2 峰值法与平均值法

正弦信号的峰值和全波整流平均值都与正弦信号的有效值成正比，存在确定的对应关系［5］，检测到正弦信号的峰值或经过全波整流后的平均值，就可以计算出正弦信号的有效值。

基于这种方法的有效值转换电路简单易行，转换速度较快，但是无法用于转换发生畸变的非典型波形信号，如晶闸管调压后的非标准正弦信号等。

1.3 数学定义法

计算交流信号真有效值的最显而易见的方法是从数学定义出发，利用乘法器和运算放大器直接进行平方、平均值和平方根计算。但是这种方法的动态范围有限，因为在平方器之后的各级必须处理振幅变化很大的信号。例如，如果输入信号的动态变化范围为100至1，那么平方器输出信号的动态范围将是10 000至1。这些限制使得此方法的输入动态变化范围最大约为10∶1。

AD采样转换是通过AD转换模块，将模拟的电流量转换为对应的数字量，然后再按照数学定义通过软件对数字量计算，算出有效值［6］。这种方法比较繁琐、复杂，其最终得到的有效值的精度还要受限于AD转换模块的量化误差、非线性误差、周期误差以及软件处理是否得当等因素［7-9］。

还有一种更好的计算方案是利用反馈在电路输入处隐式或间接地进行求平方根计算。平均值信号除以输出的平均值后，将与输入的真有效值呈线性变化(而非平方关系)。与直接从数学定义计算的电路相比，这种隐式电路明显扩大了输入的动态范围。隐式真有效值计算与其他方法相比具有器件较少、动态范围较大、成本通常较低的优点。AD公司生产的AD637芯片就是利用这一技术，本文将围绕AD637芯片的应用展开分析。

2 有效值转换电路设计过程

2.1 AD637特点及内部结构

AD637是适用于任意复杂波形的高精度真有效值/直流转换器。精度高，输入电压有效值0～2 V时，最大非线性误差为0.02%.它能计算任何复杂波形的真有效值、平方值、均方值、绝对值，并有分贝输出，量程为60dB。适用的波峰因数较宽，波峰因数为10时，附加误差仍小于1%，常见的周期性非正弦波的波峰因数在1～3之间，最多不超过5，因此AD637能够测量绝大多数的非正弦波有效值。频带宽，当输入信号电压Vin=200 mV(RMS)时，频率上限为600 kHz;Vin≥1 V(RMS)时，频率上限高达8 MHz。量程宽，只要调节供电电源的电压，其量程在0～7 V(输入信号有效值)范围内连续可调，并且有过电压保护功能。

AD637常见有SBDIP-14、CERDIP-14、SOIC_W-16等3种形式的封装，本文选用磁隔离型SOIC_W-16封装。基于磁隔离技术的磁耦均带有25 kV/μs的瞬态共模抑制能力，且能够在电压差峰值560 V的环境下正常工作。磁耦器件可提供5 000 V(rms)/ min及6 000 V/10 s的电压隔离保护，磁耦芯片内部含有施密特电路，能够对输入输出的电路滤波整形，可直接与各种高速控制芯片直接连接，如:DSP、ARM等。其内部主要包括5部分:(1)全波整流器;(2)对数平方器;(3)除法器;(4)反对数器;(5)滤波器。各部分之间的连接关系如图1所示。

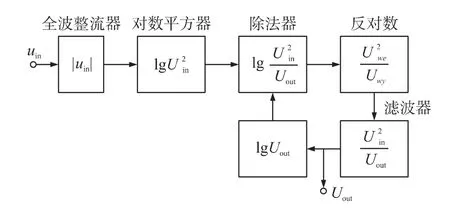
图1 AD637芯片内部架构图

2.2 有效值转换电路的结构及实施方式

有效值转换电路的结构框图如图2所示。

图2 有效值转换电路的结构框图

具体实施方式为:采用电流传感器将大的非正弦电流信号转换为小电压信号。然后将小电压信号输入有效值转换芯片AD637的输入端，AD637的输出端接AD(模拟/数字)转换模块的输入端，由AD转换模块采样处理后输出给下一级。

AD637输出端信号的大小取决于输入端信号的大小，由于常见的AD输入端最大可接受的直流电压不超过3.3 V(如DSP、STM32单片机自带的AD等)，当输入AD637的小交流电压信号有效值为3.0 V时，AD637输出直流信号的最大值为3.22 V，因此输入AD637的电压有效值不要超过3.0 V。

AD637的供电电源范围±3 V～±18 V。AD637在±5 V的供电电压下，输入交流电压的有效值最大为4 V，但是输入信号一旦超过4 V，其输出将会产生严重的非线性失真。AD637在不同的供电电源下最大输出直流电压与供电电压的关系如式(1)所示:

其中Vs为供电电压，Vout-max为最大输出直流电压(有效值)。当Vs=5 V时，Vout-max=3.67 V＞3.3 V，因此在±5 V供电，最大输入电压有效值为3.0 V的条件下，AD637可以工作在正常状态。如果Vout-max＜3.3 V，则会造成在Vout-max～3.3 V之间的数据不能正确读出。综上分析，本文采用±5 V的电源供电。

3 转换电路的实验及结果分析

本文按照AD637典型应用电路图建立了电流转换电路如图3所示。

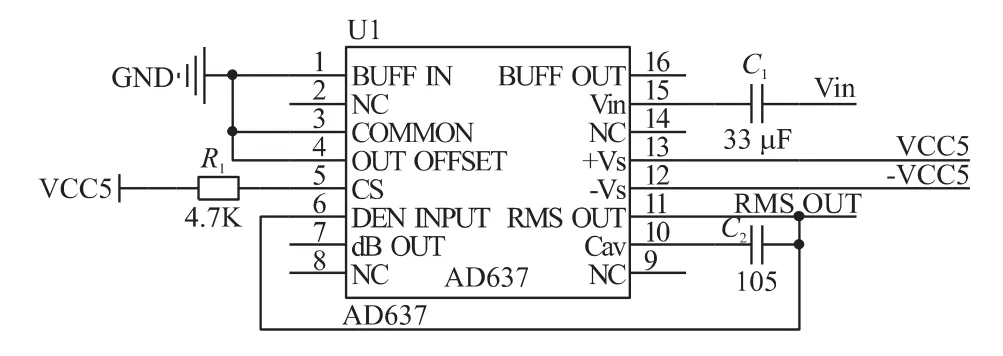
图3 AD637典型应用电路原理图

待测交流电压信号从Vin(引脚15)输入，通过一个33 μF的电容，滤掉待测信号中的直流成分。AD637的滤波器包含一个运算放大器/积分器，其平均值时间常数由片内25 kΩ反馈电阻和外部平均值电容CAV设置。转换电路的建立时间ts为:

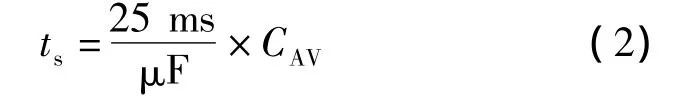
从式(2)可见，建立时间的大小只与CAV有关。建立时间应比所测量的最低频率的周期长，同时应使建立时间在合理范围内。本文所设计的有效值转换电路的CAV选为1 μF，对应25 ms.

输入50 Hz的非典型方波信号，通过原理图如图3所示的转换电路，波形如图4所示，从波形图中可以看出，输出直流信号含有较大的纹波，频率为50 Hz，其纹波峰值为220 mV左右，摆动幅度较大。

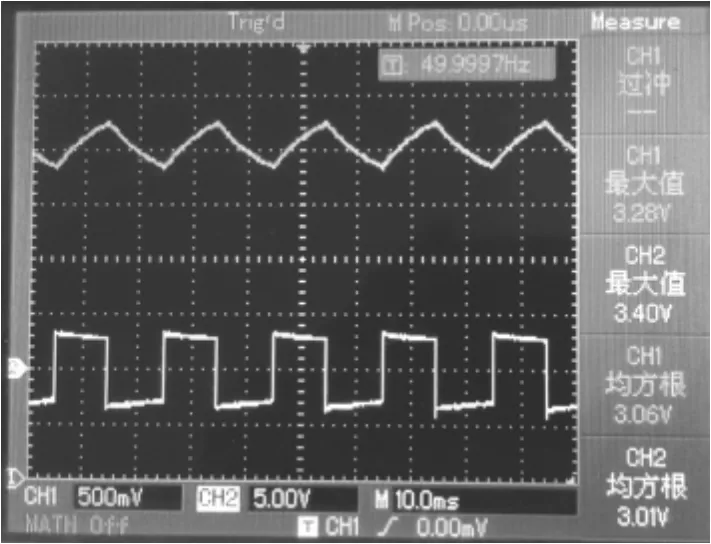
图4 50 Hz的非典型方波信号在AD637典型电路下的输出波形图

转换器的输出中含有直流误差分量和交流误差分量。直流误差为输出信号平均值与理想输出之间的直流电压差，交流误差是以输出纹波的形式存在的。这两个误差分量都是输入信号频率F和平均电容CAV的函数。总误差定义为直流误差分量的值与交流纹波分量的峰值之和。直流误差的大小与1/F2有关，即当输入信号的频率加倍时，直流误差将减小为原来的1/4，只要输入正弦信号的频率大于1/T，则直流误差将小于读数的0.2%.

定义“%纹波”为纹波输出百分数，表示输出纹波的峰值占总输出的百分数。其计算公式如式(3)所示。

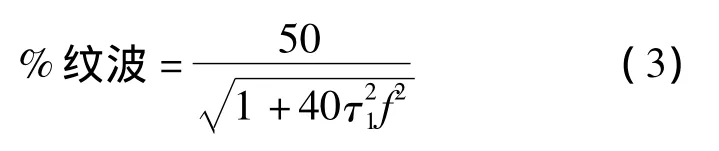
在输入信号频率为50 Hz，平均电容CAV取1 μF，则可由式(3)计算得纹波输出百分数为6.27%。

此纹波分量可以采用后置滤波电路或者增大平均电容CAV的值来减少。但是增大平均电容CAV的值会产生两个问题:(1)随着平均电容值CAV的增大，电容元件的体积也会变大。(2)建立时间会随平均电容值的增大而增加。因此，减少纹波的最好方法是采用后置滤波网络。

当频率一定时，通过低通滤波器，可以显著降低转化器输出的纹波，而直流误差的大小仅取决于平均值时间常数，无法通过这种后置滤波电路来减小。

为了提高转换电路的精度，适用于复杂电磁环境，本文在AD637典型应用电路的基础上做了改进，改进后的转换电路原理图如图5所示。

图5 基于Sallen-Key滤波电路的有效值转换电路原理图

由于AD637的输出信号与供电电源的稳定程度关联度较高，电源波动会影响输入信号失调调整的精度，因此我们在供电电源与AD637的电源引脚(12、13)之间放置两个10μF的电容，作为电荷池，起到稳定供电电源的作用。C3、C8及R3、R4构成后置Sallen-Key双极点滤波电路，C7为平均值电容。

Sallen-Key低通滤波器的传输特性如式(4)所示:

在R3=R4=R的情况下，电容的计算公式为:

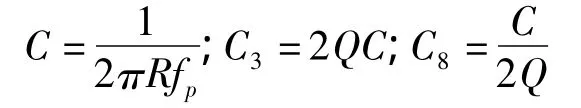
输出纹波的频率为50 Hz，现在要通过设置合理的滤波电路参数，将输出纹波的频率降低到5 Hz以内。当R3=R4=2.4 kΩ，C3=2.2 μF，C8=1.1 μF时，则滤波电路截止频率为4.6 Hz，满足要求。

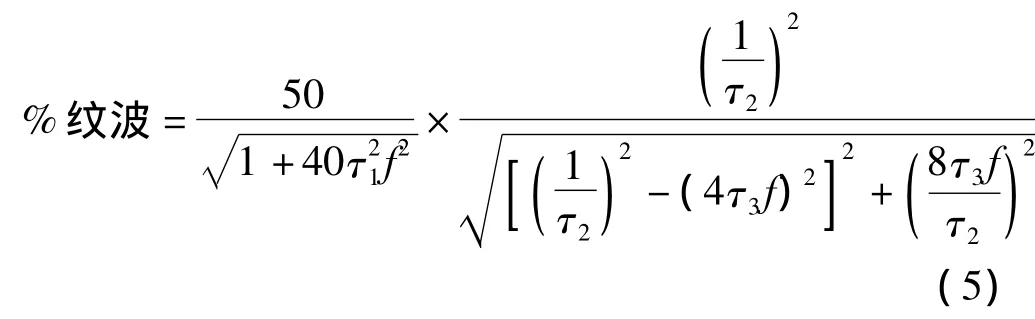
图6 50 Hz非典型方波信号在改进后电路下的输出波形图

可以看出，采用Sallen-Key滤波电路滤波后，输出信号的纹波含量大大减小，其值为20 mV左右，转换电路的输出波形十分平整，接近一条直线。

按式(3)、式(4)计算，纹波输出百分数为0.058%，而典型应用电路的纹波输出百分数为6.27%.理论上，采用Sallen-Key滤波电路滤波后可将纹波输出降低为典型应用电路的1%以内。

4 结论

Sallen-Key滤波电路对减小总误差作用显著，在AD637典型电路中，输出的纹波误差可达总误差的99%以上，直流误差在1%以下，总误差基本是由纹波误差产生的。而对于改进后的Sallen-Key滤波电路，直流误差是主要的误差来源，大约占总误差的95%左右，两种电路的直流误差相差不多，后置滤波电路略有增大。由此可见，Sallen-Key滤波电路对于减小纹波输出、减小总误差的效果是十分显著的。

［1］ 闫晓，钱晓龙，汪晋宽.一种电流真有效值测量智能传感器设计［J］.仪器仪表学报，2003，24(4):107-123.

［2］ 陈仁伟，朱长青，岳夕彪.高准确度有效值转换电路的设计与实现［J］.电子测量技术，2010，33(6):20-22.

［3］ 白佳宁，史仪凯，张金勇.基于MSP430的非正弦周期信号有效值检测仪表研究［J］.工业仪表与自动化装置，2009(3):3.

［4］ 李荣武.AD637集成真有效值转换器［J］.电测与仪表，1991 (3):15.

［5］ 杨善水，张旭明，张卓然，等.基于有效值检测的航空变频交流发电机调压技术［J］.南京航空航天大学学报，2010，42(6): 717-721.

［6］ 胡华波，武建文，张路明，等.电信号有效值测量综合误差分析与模型［J］.电工技术学报，2012，27(12):172-177.

［7］ 李沂乘.采样计算方法测量交流电压有效值误差分析［J］.电子测量与仪器学报，2008(增刊):62-65.

［8］ 胡虔生，杨存祥.同步误差对非正弦周期电信号测量精度的影响［J］.微特电机，1996(1):27-28.

［9］ 张欣，向馗，何闻，等.一种高精度的正弦信号有效值数字化测量方法［J］.东南大学学报，2001，31(5A):117-119.

孟彦京(1956- )，男，教授，研究方向为电力电子与电力传动;

李林涛(1986- )，男，河南唐河人，在读硕士研究生，电力电子与电力传动lintaowonder@163.com。

A Low Ripple Output RMS Conversion Circuit of Nonstandard Sine Current

MENG Yanjing*，LI Lintao，GAO Xiaoxiao，XIE shihong
(Electrical and Information Engineering，Shaanxi University of Science and Technology，Xian，Shaanxi 710021)

The article first introduces the methods currently used for the current rms conversion，analyses of the characteristics of each method and sets up a typical application circuit with AD637 chip，as a core.By analysing the entering the Rectangular wave signal，the higher levels of output ripple are found，and the output contains a large error. Based on the AD637 typical application circuit，a Sallen-Key filter circuit-based nonstandard sinusoidal current RMS conversion circuit was set up，and by optimizing the parameters of the filter circuit，the output ripple decreases less than 1%of the typical application circuit to improve nonstandard sinusoidal current signal RMS conversion accuracy.

electronic circuit;low ripple;allen-Key filter;current detection;nonstandard sinusoidal signal;RMS;AD637

10.3969/j.issn.1005－9490.2014.02.019

TM933

A

1005－9490(2014)02－0258－04

2013-05-23修改日期:2013-07-07

EEACC:1290D