一种基于Cholesky分解的快速矩阵求逆方法设计

魏婵娟，张春水，刘 健

（中国空间技术研究院航天恒星科技有限公司 北京 100086）

抗干扰接收机由于增加了抗干扰处理的部分将会对导航信号的实时解算造成一定的影响，求取抗干扰滤波权值用时越长，对解算的延迟越大，造成的定位误差也将越大。在权值更新以及抗干扰滤波的整个处理过程中，矩阵求逆的用时占用了90%以上的时间，矩阵求逆用时过长是导致接收机权值更新过慢的最主要因素，因此若采用直接矩阵求逆对抗干扰算法进行实现，必须保证矩阵求逆的用时极短。本文针对大维数赫米特矩阵求逆实现方法进行FPGA设计及实现。

1 Cholesky分解求逆方法及其流水设计

A为正定的赫米特矩阵，采用Cholesky分解矩阵求逆方法的实现过程为[1]:

1）由Cholesky分解得到下三角矩阵L及其共轭转置矩阵LH，A =L×LH；

2） 对下三角矩阵L进行矩阵求逆计算，得到其逆矩阵IL=L-1；

3） 由IL矩 阵 求 得A的 逆 矩 阵IA，IA =（LH）-1×L-1=LH×IL。

在FPGA实现赫米特矩阵求逆的关键在于实现方法的流水设计，合理高效的流水方法可以最大程度地节约资源提高实现速度，以下分3部分实现赫米特矩阵Cholesky分解求逆的实现方法设计[2-4]。

1.1 矩阵的Cholesky分解

对A矩阵进行Cholesky分解，得到下三角矩阵L，A=LLH。采用分块的方法计算L矩阵[5]。

将矩阵L及A进行分块表示如下：

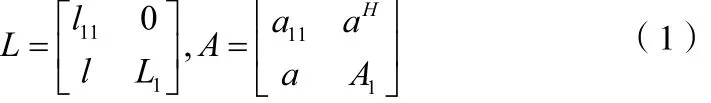
由A=LLH推导可得：

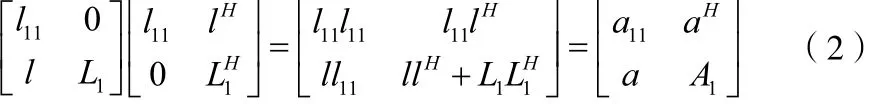
根据如上公式表示，L的第一列的值可由A的第一列的值获得，其计算方法为：

在计算完L的第一列的之后，之后需要计算L1，根据式2可得:

在将A矩阵的部分更新为A1-llH后，可采用相同的方法计算出L1矩阵的第一列的值，即L矩阵的第2列的值，依次类推可计算出L的所有值。

对以上的Cholesky矩阵分解方法进行FPGA实现的流水设计，以4×4矩阵为例，可分为四步分析各个数据之间的依赖关系并计算L各列的值。

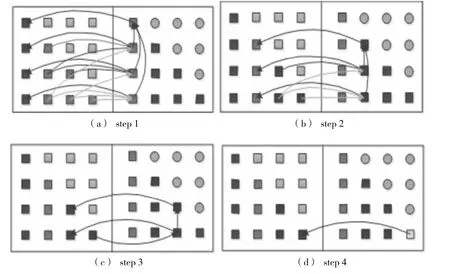
图1 矩阵Cholisky分解步骤图Fig.1 Four steps of Cholisky decomposition

步骤1：计算L矩阵的第1列；之后更新A矩阵（图中，左侧的矩阵为A矩阵，右侧为L矩阵，箭头所指向的方向为计算当前值所依赖的数据，例如将头由a指向b，表示计算a时需要用到b，需在b计算完之后才可进行a的计算）。

步骤2：计算L矩阵的第2列；之后更新A矩阵。

步骤3：计算L矩阵的第3列；之后更新A矩阵。

步骤4：计算L矩阵的第4列；A矩阵无需再更新。

对于4×4矩阵，在经过4步之后可获得L矩阵。

1.2 下三角矩阵求逆

对下三角矩阵L进行求逆计算得到的逆矩阵IL[6]，根据L*IL=E，分别求得IL各列的值。

L矩阵求逆数据依赖关系及流水设计如图2所示。

步骤1：计算IL对角线上的值（图中，左侧的矩阵为L矩阵，右侧的矩阵为IL矩阵）。步骤2：计算IL第二对角线上的值。步骤3：计算IL第三对角线上的值。步骤4：计算IL第四对角线上的值。

通过对对角线上的值进行同步计算，在经过4个步骤之后可计算出IL矩阵的所有值。

1.3 矩阵相乘

上三角矩阵LH与下三角矩阵L相乘得到A的逆矩阵IA，IA=ILHIL。

矩阵相乘流水设计数据间的依赖关系（图中左侧矩阵为L矩阵，右侧矩阵为IA矩阵）。

矩阵相乘较为简单，其各个数据间的计算无需等待，仅仅依赖于已知的下三角矩阵IL。

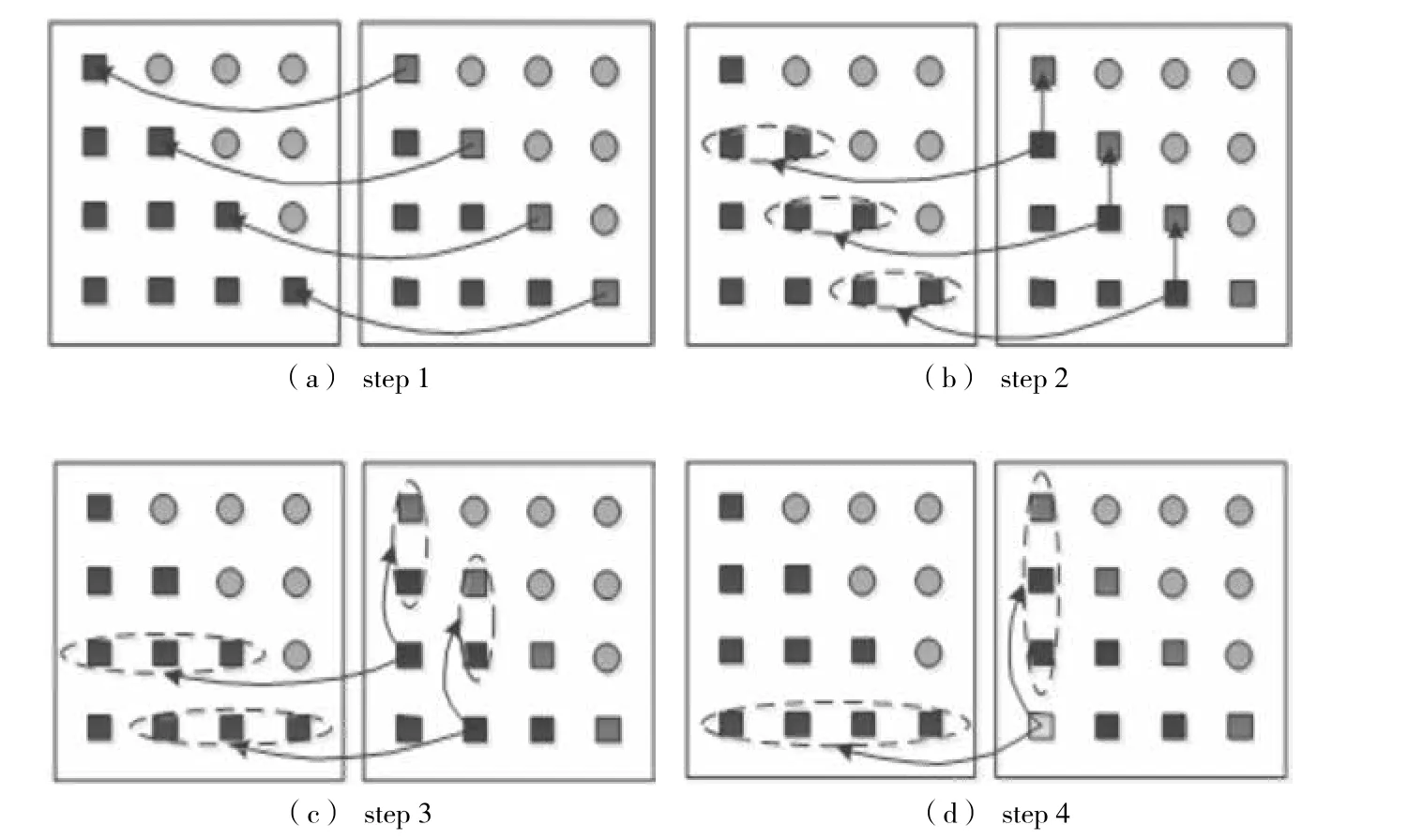
图2 下三角矩阵求逆数据依赖关系图Fig.2 Data dependency relationship of lower triangular matrix inversion

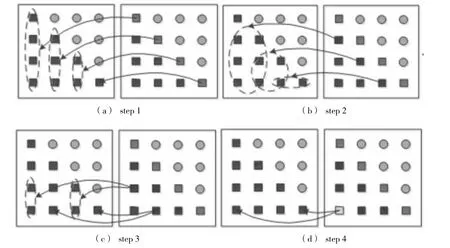
图3 矩阵相乘的数据依赖关系图Fig.3 Data dependency relationship of matrix vector multiplication

矩阵相乘较为简单，其各个数据间的计算无需等待，仅仅依赖于已知的下三角矩阵IL。

2 FPGA实现

2.1 状态控制及功能描述

与1节Cholesky分解求逆流水方法对应，FPGA硬件实现电路包括3个主要模块：Cholesky分解、下三角矩阵求逆和矩阵相乘。其在FPGA中实现的状态控制及存储如下图所示：

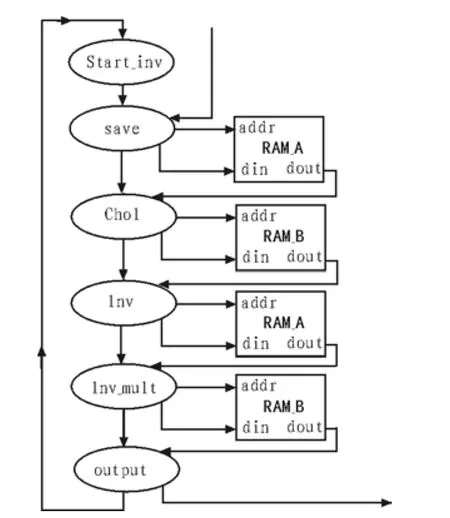
图4 FPGA实现Cholesky矩阵分解求逆状态控制图Fig.4 FPGA implementation of Cholesky decomposition and inversion

功能描述：

1）Start_inv为矩阵分解求逆开始标志，save状态下，将生成的协方差矩阵存入RAM_A；

2）Chol状态下完成协方差矩阵的Cholesky分解，得到的下三角矩阵L存入RAM_B；

3）Inv状态下完成下三角矩阵的求逆计算，将得到的逆矩阵IL存回RAM_A；

4）Inv_mult状态下完成ILH矩阵与IL矩阵的相乘，即上三角阵与下三角阵的相乘，其结果存入RAM_B。

5）在Inv_mult状态结束后进入Output状态将RAM_B中的逆矩阵输出。

6 ）在Ouptput状态结束后重新返回start状态，开始对下一组协方差矩阵的分解求逆。

2.2 用时测试

跟据以上的流水设计进行FPGA代码的编写实现，矩阵求逆的整体用时如下表所示：

表1 FPGA实现Cholesky矩阵求逆用时Tab.1 FPGA implementation time table

由上表看出，28×28维矩阵的求逆用时小于0.4 ms，35×35维矩阵的求逆用时仅需不到0.8 ms。

3 结 论

文中针对大维数赫米特矩阵的求逆的问题展开，介绍了适用于正定赫米特矩阵的Cholesky矩阵分解求逆方法，并对该方法进行了高效的流水设计，分3步实现矩阵的FPGA分解求逆，经过试验测试，用时极短。

[1]张贤达.矩阵分析与应用[M].北京:清华大学出版社, 2004.

[2]郭磊.矩阵运算的硬件加速技术研究[D].长沙:国防科学技术大学, 2010.

[3]Thompson, J. Benkrid, K. Xuezheng Chu. Rapid Prototyping of an Improved Cholesky Decomposition Based MIMO Detector on FPGAs [J].Adaptive Hardware and Systems, 2009(4):369-375.

[4]Mach D M,Koshak W J.General matrix inversion for the calibration of electric field sensor arrays on aircraft platforms [J].Marshall Space Flight Center, 2006(6):1576-1587.

[5]鲁翠仙.分块矩阵在矩阵求逆中的应用[D].昆明:云南大学,2009.

[6]彭玲,彭大芹. 一种下三角复矩阵求逆方法的IP设计与实现[J].电子测试, 2011(10):9-12.

PENG Ling, PENG Da-qin.IP design and implementarion of lower trlangular matrx invertion[J].Electronic Test,2011(10):9-12.