GPS系统与全站仪的组合测量

徐建龙

（中国飞行试验研究院 陕西 西安 710089）

在我院许多试飞任务中，都需要对试验场地的位置进行标定，给出所需标定点GPS坐标、定出所需要的方向、距离等数据。用以给飞行员指示目标，或将地面测量的数据与机载设备记录的数据相对比，评估飞行试验的结果等。进行这些任务时，都需要利用GPS设备进行测量。

1 任务概述

在某课题的地标数字化任务中，需要测量机场上所画出的地面标志的大地坐标，用以与飞机飞行时记录的机载GPS数据相对比。由于当时尚未配备实时差分GPS系统，而用大地测量型GPS进行精确测量所需的时间较长，一个点就需要测量40分钟以上，但总共所需测量的标志点有近百个，测量又不能影响正常的飞行，只能在没有飞行计划的间隙时间进行，因此只用GPS系统逐个点地进行测量是不切实际的。所以，结合我们配备的全站仪测量速度快、精度高，而且待测点附近地域开阔，可相互通视的特点，采取用GPS精确测量这些待测点中的几个关键的控制点，同时用全站仪将全部待测点的相对空间坐标测量出来，然后通过已知GPS坐标的几个点和其余的点的空间位置关系来计算出所有待测点的GPS坐标。通过这一方法达到了迅速、准确测量效果，圆满地完成了任务。

2 仪器介绍

我们配备的GPS系统是由两台ASHTECH Z-12型大地测量GPS接收机组成，其中一台作为基准站而另一台作为活动测量站，共同组成事后差分GPS测量系统。其具有测量范围大，精度高等特点，在为飞行实验建立大范围的精确测量场的过程中有广泛的应用。但是其也有使用限制：测量时间较长；测量天线上方及附近不能有遮挡或强烈反射卫星信号的建筑物或物体；需要远离高压电线、信号塔等能发射强烈电磁辐射的物体等，而且由于其需要接收卫星信号，测量时的天气对其精度也有一定的影响。通常，在天气晴朗、四周开阔、附近没有较高遮挡物的情况下进行40分钟连续的测量，其差分结算的结果可以达到厘米级以下，但由于差分基准点的精度在3厘米左右，故而总的测量精度可以认为是4厘米[1]。

全站仪的全名为全站速测仪，具有测角、测距等功能，其特点是测量精度高，测量速度快。当然全站仪的测量也有一定的限制，如测站与目标之间必需通视、测量范围受大气条件影响等。

此次测量中所用到的全站仪的主要技术参数如表1、表2所示。

表1 全站仪的主要技术参数Tab.1 Specif i city of electronic total station

上述两种仪器都有各自的优缺点，而将两种仪器有机地结合起来使用，取长补短，就能大大的提高他们的效能，弥补不足之处。

表2 全站仪的主要技术参数Tab.2 Specif i city of electronic total station

3 坐标转换

GPS与全站仪采用的是两种不同的坐标系统：GPS采用的是WGS-84世界大地坐标系，而全站仪的数据一般为以自身旋转中心为原点、水平某一指定方向为X轴、竖直方向为Z轴、Y轴与Z轴构成右手直角坐标系。将两种仪器的应用完美地融合起来的关键就是其测量数据在不同坐标系中的相互转换，通过数据的坐标转换将测量得到的数据变成我们所期望得到的结果。

为此，我们还需要一个转换的“介质”：一种与两种坐标系都有联系的坐标系以用作转换的中间环节，我们采用的是空间大地直角坐标系，其原点与WGS-84世界大地坐标系的原点相同，都是地球的质心，X轴指向BIH1984.0的零子午面和CTP赤道的交点，即经度的零度；Z轴指向BIH1984.0定义的协议地球极（CIO）方向，即北纬90度；Y轴与Z轴构成右手坐标系。

3.1 经纬度与空间大地直角坐标系的相互转换

假设某一点的位置用空间大地直角坐标系[2]表示为（X，Y，Z），用大地坐标表示为（B，L，H），则有：

式中N为该点的卯酉圈曲率半径，

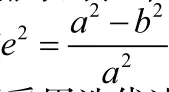
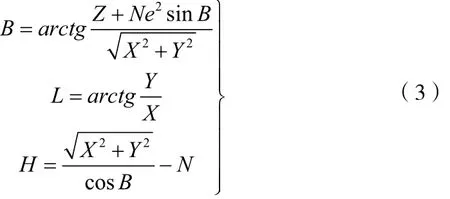
其中B的初值一般取，在计算时设定一个足够满足需要的精度即阀值，当前后两次计算出来的差距小于这个阀值时，即可以认为计算得到的结果可以满足精度要求。

3.2 不同空间直角坐标系之间的坐标换算

对于不同的空间直角坐标系[3]，如全站仪坐标系和空间大地直角坐标系，如果用两个三维空间直角坐标系OT-XTYTZT和OG-XGYGZG分别来表示全站仪坐标系和空间大地直角坐标系，其相互关系可以表示为：

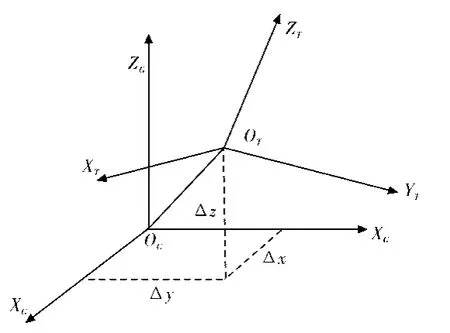
图1 坐标转换Fig. 1 Coordinates switchover

则同一点P在OT-XTYTZT中的坐标（XT,YT,ZT）换算为OG-XGYGZG中的坐标（XG,YG,ZG）的关系式为：

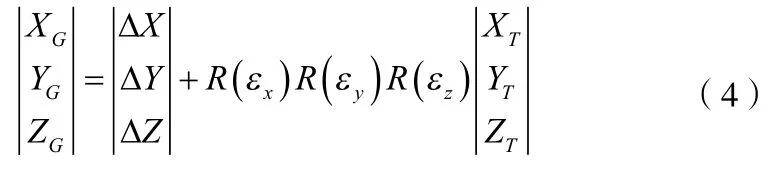
其中 ， ， 为旋转矩阵，其表达式为：

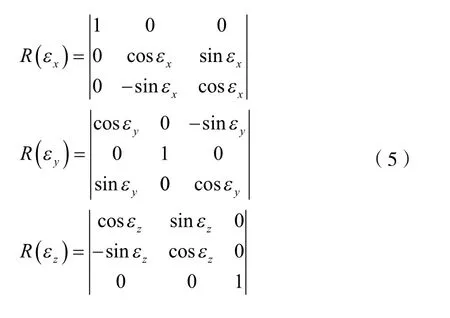
其中（ΔX，ΔY，ΔZ）是全站仪坐标系原点在空间大地直角坐标系中的坐标；（εx，εy，εz，）是全站仪坐标系的坐标轴与空间大地直角坐标系的坐标轴的夹角。

如果两个坐标系所采用的度量单位不一致时，还需要考虑到两个坐标系间的尺度比因子κ，则完整的转换公式是：

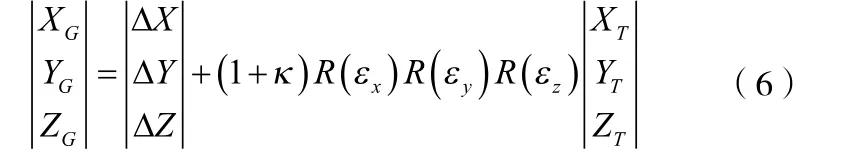
式中的 ΔX，ΔY，ΔZ，κ，εx，εy，εz被称为两坐标系间的转换参数，其中ΔX，ΔY，ΔZ为平移参数，κ为尺度比参数，εx，εy，εz为旋转参数。

由此可以看出，只要已知或确定了两空间直角坐标系之间的转换参数，就可将任一点的坐标从一个坐标系转换到另一个坐标系。

4 任务执行

在实际的飞行任务中，将GPS与全站仪进行综合应用主要就是利用GPS大地经纬度精确测量能力和全站仪小范围内的精确、快速测量功能相结合、互补不足之处。以下就结合本次测量任务进行说明：

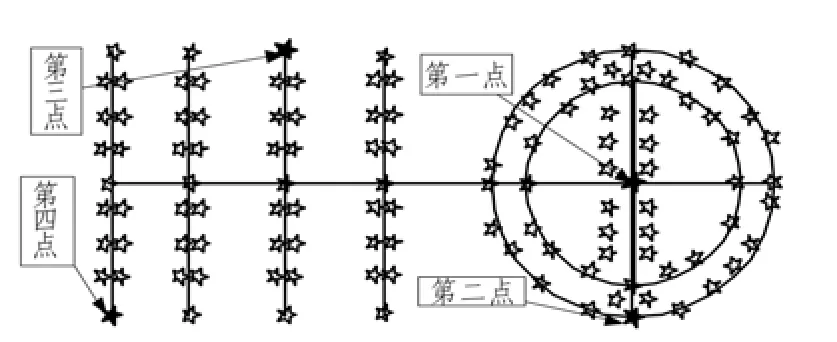
图2 本次任务的待测点Fig. 2 Sites need to measured in this assignment

根据该任务的具体需要，需要测量的是图中用五角星表示的点的坐标。由于主要的点位是双圆环上及内部的点，其余四条直线上及附近的点是作为辅助的点位，故而在圆心及圆环各选一个点用GPS进行精确测量，用作坐标转换的基准，即图中的第一点和第二点。在直线上再选择两个合适的点进行GPS精确测量，用作效验转换的精确度之用，即图中的第三点和第四点。全站仪就架设在圆环附近合适的位置，并且使测量范围能够全部覆盖待测点。

在本次试验中，采用的是索佳SET II C全站仪，合作目标为带有延长杆和圆形水准器的徕卡小棱镜。任务执行时，先将GPS架设好，开始进行测量。由于GPS架设好开始测量之后，只要注意在测量期间不要让接收天线的位置发生变化，就不用再进行另外的操作了，所以工作人员可以同时操作全站仪对各个点进行测量。至于被GPS天线占用的点，可在该点的GPS测量完成移至下一个点测量时用全站仪测量。如此，两种测量可同时进行，节约大量时间。

5 数据处理

测量完成以后，即可对数据进行处理，主要有以下几个步骤：

1）利用配套软件解算出GPS测量得到的结果，再利用公式（1）得出第一、二两点空间大地直角坐标系，进而计算出这两点连线的方向与真北方向的夹角；同时还要计算出这两点连线在全站仪坐标系中与各坐标轴的夹角。

2）根据公式（6）将各待测点的坐标转换成空间大地直角坐标系中的坐标。

3）依照公式（3）计算得出各点的大地经纬度。

其中，第2）步中需要用到的平移参数就是圆心点在全站仪坐标系中的坐标；根据第一步计算得到的第一、二两点连线与真北的夹角、两点连线在全站仪坐标系中与各坐标轴的夹角、圆心点的大地坐标等数据即可得到所需要的旋转参数；由于大地坐标系和全站仪坐标系都是采用国际标准度量衡尺度，即两坐标系中的单位长度是相同的，故而κ=0。

整个任务的流程图如下：

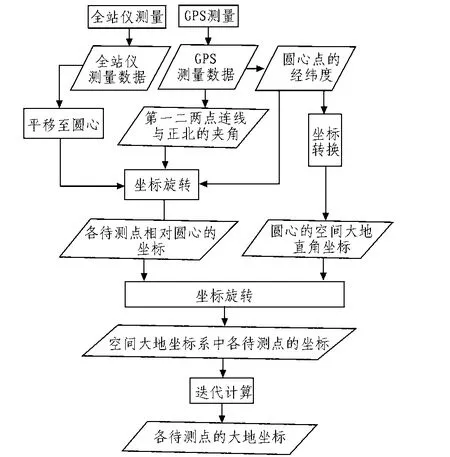
图3 任务流程图Fig. 3 Flow chart of assignment

6 误差分析

无论怎样的测量都是为最终的任务服务的，只有满足任务的需求测量才有意义，而对于数据，其精度是非常重要的指标。在本次任务中，最终的结果数据的精度主要取决于GPS系统的测量精度、全站仪测量数据的精度以及进行换算的过程中产生的误差[4-6]。

在此次测量任务中，为了准确地得到作为基准的两个点的GPS坐标，圆心和圆环上的点分别测量了114分钟和140分钟，记录的数据解算结果精度分别为±7.071 1 mm和±6.708 2 mm，而GPS系统本身的测量精度为3 cm。而全站仪的测角精度为2 s，测距精度为2 mm+2 ppm。在迭代计算中采用的阀值为[7-8]10-7（经纬度）秒。即：

表3 数据精度验证Tab.3 Data precision validation

即 σ总方根 ≈0.031 4 m

由于在本课题中，数据的最后要求精度为0.05 m，故而可以看出，无论是最后结果的极大误差或是平方根差误的精度均可以满足要求。在本次测量中的两个校验点的测量数据与实测数据的差均在0.03 m以下就证明了这一点。

7 结 论

根据本次测量的实际效果，可以确定采用GPS和全站仪结合测量的方法测量大批量待测点的坐标，能够准确、迅速地完成测量任务，并且最终得出的数据精度也能满足任务的要求。

[1]国家质量技术监督局，GB/T 18314-2001，全球定位系统（GPS）测量规范[S].北京:中国标准出版社，2001.

[2]胡友健，罗昀，曾云.全球定位系统（GPS）原理与应用[M].武汉:中国地质大学出版社，2003.

[3]尤承业.解析几何[M].北京:北京大学出版社，2004.

[4]朱正华,黄建刚,吴凤英.一个间接测量误差传递公式的普遍证明[J].湖南大学学报:自然科学版, 2001(S1):5-7.

ZHU Zheng-hua, HUANG Jian-gang,WU Feng-ying. A universal proof of error transferring formula of Indirect measurement[J].Journal of Hunan University:Natural Sciences Edition,2001(S1):5-7.

[5]唐文强,韦明德,杨端翠.大学物理实验[M].广州:华南理工大学出版社, 2003.

[6]邓春芳.间接测量误差分析及数据处理[J]. 北京信息科技大学学报:自然科学版，2010, 25(4):79—81.

DENG Chun-fang，Analysis of indirect measurement error and data processing[J]. Journal of Beijing Information Science and Technology University: Natural Sciences Edition, 2010,25(4):79—81.

[7]杨倩，问婷婷，李红，等.基于小波与阈值的图像分割[J].现代电子技术，2012(24):54-55,58.

YANG Qian, WEN Ting-ting,LI Hong,et al.Image segmentation based on wavelet and threshold[J].Modern Electronics Technique, 2012(24):54-55,58.

[8]张晓宁,孙丽君.一种改进的小波阈值信号去噪方法[J].电子科技，2012(11):15-17,24.

ZHANG Xiao-ning，SUN Li-jun.An improved method for wavelet threshold signal demonizing[J]. Electronic Science and Technology，2012（11）:15-17，24.