基于定步长自然梯度算法盲混合信号分离技术研究

李留青，陈中良

（黄淮学院 河南 驻马店 463000）

基于定步长自然梯度算法盲混合信号分离技术研究

李留青，陈中良

（黄淮学院 河南 驻马店 463000）

本文利用自然梯度算法对盲混合方波、正弦波、调幅波和噪声等信号进行盲分离实验，通过仿真，验证了自然梯度盲分离算法在复杂信号分离中的准确性。比较了不同步长下，自然梯度算法的分离性能，得出步长的选择对算法收敛性及稳态误差的重要性，文章分析了算法在步长变化情况下的收敛速度，稳态性能等。

盲信号；分离技术；自然梯度算法；稳态性能；收敛速度

盲分离技术[1]是指源信号未知以及在进行盲混合过程未知的情况下，将盲混合在一起的信号分离出混合前源信号的一种方法。在当今的信号处理研究领域中，信号的盲源分离研究是目前一个具有极大挑战性的信号分离研究的热点，“鸡尾酒会”问题，是人们对盲分离问题的深入研究[2]。当人们在一个噪音嘈杂的环境中，如果若干人在同一时间同时说话，如何实现仅凭探测器检测到的噪音加语音的混合语音信号，就能从混合语音信号中分离出人们所需要的声音信号呢？这就是信号分离研究的热点：盲源分离问题[3]。盲分离问题的有非线性混合、线性瞬时混合和线性卷积混合3种基本模型。无监督学习法是进行盲分离最常用的方法，该方法首先根据一定的理论，来构造出合适的目标函数，在确定了目标函数后，然后通过合适的寻优算法就能够求解得到需要的解混矩阵。本文研究一种固定步长的自然梯度盲分离算法在不同类型信号的盲混合模型中的分析和应用，并研究步长在算法性能中的作用。

1 盲分离模型

1.1 ICA模型

图 1 为 ICA 盲源分离模型图[4]，图中 S1（t），S2（t）， ...，Sn（t）表示未知的源信号，混合系统A是信号的传输通道，N表示噪声，x1（t），x（t），...，xm（t）表示观测到的混合信号，W 是需要求解的分离系统，通过分离系统能够很好的得到未知源信号的最佳估计，y1（t），y2（t），...，yn（t）即为所求源信号的最佳估计。

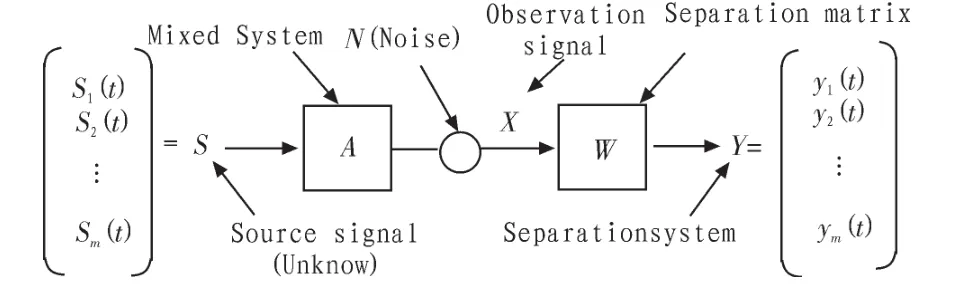
图1 盲信号分离框图Fig.1 Fanaticism separation diagram

如果从噪声信号有无的角度来分，可分为：有噪模型和无噪模型两类。由于有噪模型、线性卷积混合和非线性混合模型，其混合方式和算法较复杂，因此，针对本文研究对象选择线性瞬时混合有噪模型。

ICA模型进行盲源分离的数学表达式如（1）所示：

式（1）中，s表示一组源信号，由n个独立信号源组成的。

s=[s1（t），s2（t），…，sn（t）]T，在经过未知传输通道 A 后，通过传感器接收到的观测信号 x=[x1（t），x2（t），…，xm（t）]T，共有m个观测信号，假设m≥n，这里系统简化为m=n。式中，s是一个由n个独立源信号构成的矩阵，A是一个未知的m×m混合矩阵，与混合系统模型密切相关[5]。

式（1）中，x是观测到了混合信号矩阵，W是求解出的的解混矩阵，Y则是通过ICA方法得到的源信号s的估计。因此说，运用ICA方法进行盲源分离的关键就在于如何求解出解混矩阵W。

1.2 ICA求解一般过程

ICA求解的一般过程主要包括：1）预处理；2）确立优化目标函数；3）选择最优的优化算法共3个步骤。其中目标函数的选取很关键，它决定了ICA的一致性和鲁棒性等等。并且目标函数的选取及收敛速度以及对计算机的内存要求等息息相关。

常用的目标函数有：高阶累积量、负熵、互信息、最大似然估计，程序基于最大似然估计进行目标函数的选取。对于ICA问题的求解来说，在选取了合适的目标函数之后，下一步工作就是要选择合适的优化算法来对已经选好的目标函数进行学习，使其达到最大值或最小值，从而求得合适的解混矩阵w，使得分离出的独立分量，与各个源信号尽可能的相等。从不同的角度来进行优化算法分类，可以分成很多类别，本文设计程序利用最大似然估计最为目标函数的选取，基于梯度的自然梯度优化算法进行盲混合信号的分离实践。

2 算法分析

随机梯度算法是一种常用来求目标函数L（W）极值的方法，其工作步骤：

Step1：选取一初始解混矩阵，将其代入目标函数，求出L（W）在 W（0）处的梯度，

Step2：在负梯度方向（如果求解最大值，则取正梯度方向），增加一个合适的步长，计算出新的分离矩阵形W（1），重复上述步骤。故求解W的随机梯度算法的计算公式为：

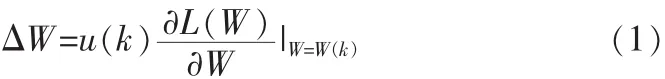
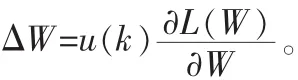
式（1）是常见的一种梯度下降法的迭代公式，对选取的目标函数L（W）不同时，可以得到不同的迭代公式。因此，本文目标函数选用最大似然估计，将Y=Wx代入最大似然估计公式：

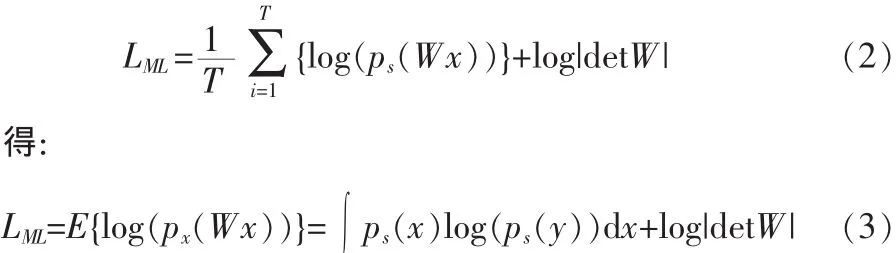
通过对其求导，得到：

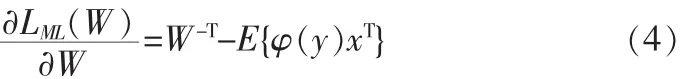
将式（4）带入式（1）可得到，解混矩阵W的迭代公式为：

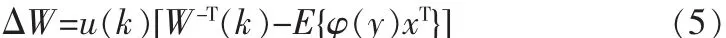
式（5）是随机梯度算法的离线批处理迭代公式，如果用瞬时值替代期望值，可得到随机梯度算法的在线自适应迭代公式：

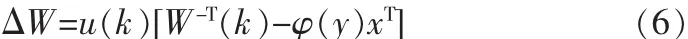
当选取目标函数L（W）不同时，得到迭代公式是不同的。这里，μ（k）为步长；g（·）为给定的非线性函数；通常，该函数与源信号概率密度函数密切相关，对于超高斯信号，g（·）=tanh（y），对于亚高斯信号，g（·）=y3。

Infomax算法可有效的分离了多个超高斯分布的源信号。但是，这一算法的主要缺点是：收敛速度慢，同时由于涉及分离矩阵W的求逆，一旦W在更新过程中条件数变差，算法就可能发散。对这一问题，Amari提出了基于黎曼（Riemann）空间的自然梯度算法。对于在矩阵空间中讨论的ICA问题来说，自然梯度与随机梯度之间存在如下关系：

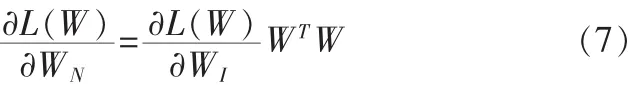
经过整理，用瞬时值 φ（y）yT代替期望值 E{φ（y）xT}时，自然梯度算法可表示为：

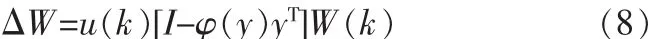
与随机梯度相比，自然梯度算法可以避免对矩阵进行求逆运算，实际数量明显降低，同时也加快了收敛速度。通过实践证明，自然梯度算法是一种具有很好分离效果的学习算法，同时该算法并不要求对观测信号进行白化处理，从而使信号处理步骤简化，已经成为了一种很常用的学习算法。

在本文中，采用以全局传输矩阵中元素独立性表示的串音误差来衡量分离性能的优劣。串音误差是由Amari最先提出来的，表示分离矩阵W的逆矩阵和混合矩阵A的偏离程度，串音误差定义为：

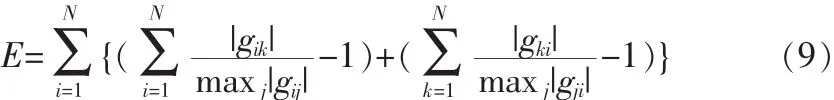
式（9）中，gij表示全局传输矩阵G=WA的元素。E是一个不小于0的数，仅当信号完全分离时E=0，实际中，当算法收敛后，串音误差是一个非常小的值[8]。

4 仿真实验

假设初始信号由方波信号、正弦波信号、调幅波信号以及噪声信号等构成，如图2所示，采样频率为1 MHz。

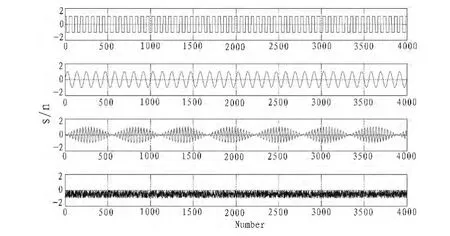
图2 初始新号波形Fig.2 Initial new waveform

采样4 000个点进行观测分析计算，初始信号通过随机矩阵盲混合后，其波形杂乱无章，很难识别，如图3所示。

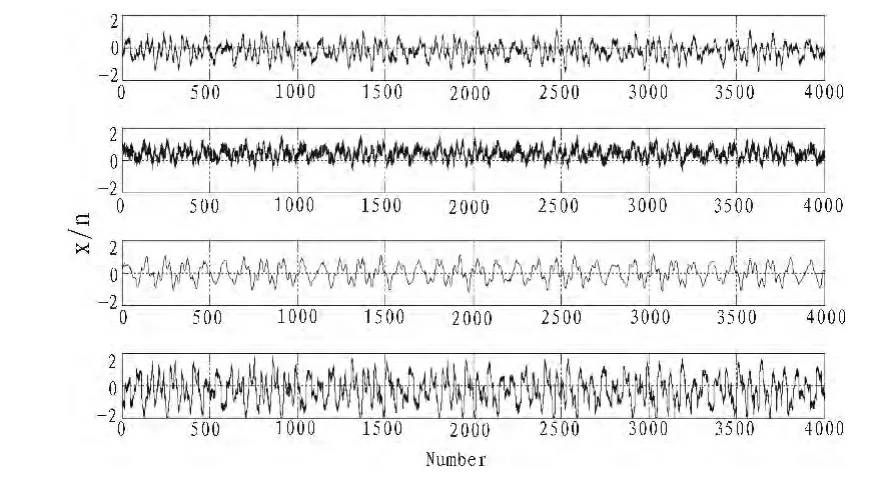
图3 盲混合信号波形Fig.3 Blind mixed signal waveform

在对采集到的观测信号进行盲分离时，采用初始步长μ=0.005的自然梯度算法对盲混合信号进行分离实践。算法中，采用非线性函数y3。分离结果波形如图4所示。

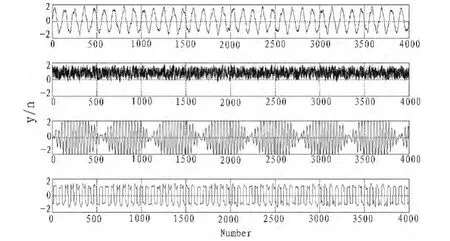
图4 分离波形图Fig.4 Separate waveform figure

从图4可以看出，本文算法能够准确的分离出盲混合后的信号。串音误差如图5所示。

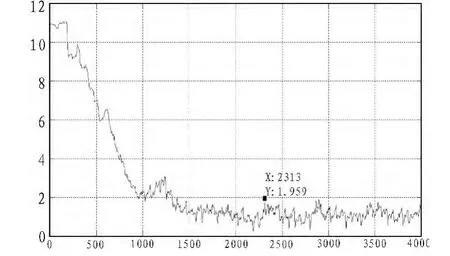
图5 串音误差（步长 =0.005）Fig.5 Crosstalk error （step length=0.005）

从串音误差图5可以看出，算法在迭代1 200次后基本实现收敛，稳态后最大串音误差为1.959。为了研究步长对分离性能的影响，采用步长0.01的自然梯度盲分离算法。算法同样能够实现对信号的盲分离，其串音误差如图6所示。

由图6串音误差图中可以看出，步长为0.01时，迭代不到1 000次即实现收敛，说明选择较大步长时，算法收敛速度快，但稳态性能较差，稳态后最大串音误差为3.453。由此看出，梯度算法对步长的选择十分敏感，微小的差异都会带来不同的分离结果。通过仿真试验可以看出，梯度算法的步长选择是一个关键的问题。今后将从步长自适应的角度进一步对自然梯度在盲混合信号分离中的作用进行研究。

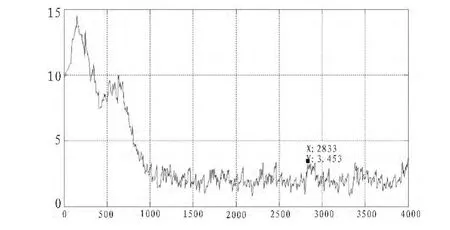
图6 串音误差（步长μ=0.01）Fig.6 Crosstalk error （step length=0.01）

5 结束语

本文介绍了自然梯度算法在盲混合信号分离中的作用，通过仿真实验表明，该算法能够对盲混合的信号进行有效分离，通过实验分析，自然梯度算法在盲分离时，具有等变化性，其顺序及相位不能确定，另外，由于算法的计算量、收敛速度和稳态性能是相互矛盾的，在步长的选取上要进行综合考虑，这也是今后研究的方向之一。

[1]马建仓，牛奕龙，陈海洋.盲信号处理[M].北京：国防工业出版社，2006.

[2]Choi S，Cichocki A.Adaptive Blind Separation of Speech Signals:Cocktail Party Problem，Korea:In Pro[C]//International Conference on Speech Processing，1997：617-622.

[3]A Bronkhorst.The Cocktail Party Phenomenon:A Review of Research on Speech Intelligibility in Multiple-talker Conditions[J].ACUST ICA，2000，86（1）：117-128.

[4]史习智.盲信号处理——理论与实践[M].上海:上海交通大学出版社，2008.

[5]Hyvarinen A，Karhunen J.独立成分分析[M].周宗潭，董国华，等译.北京:电子工业出版社，2007.

[6]Hyvärinen A，Oja E.A Fast Fixed-Point Algorithm for Independent Component Analysis[J].Neural Computation，1997，9（7）：1483-1492.

[7]杨福生，洪波.独立分量分析的原理与应用[M].2版.北京:清华大学出版社，2006：20-24.

[8]Amari S，Cichocki A，Yang H H.A new learning algorithm for blind signal separation[C]//in Advances in Neural Information Processing Systems.NIPS’1995.Cambridge，MA:MIT Press，1995：757-763.

Research of natural gradient algorithm blind signal separation

LI Liu-qing，CHEN Zhong-liang
（Huanghuai University， Zhumadian 463000， China）

In this paper， using the natural gradient algorithm for blind mixed Fang Bo，sine wave， amplitude modulation wave and noise signal blind separation experiments， simulation， verified the accuracy of the natural gradient blindseparation algorithm in complex signal separation.Comparison of differentsteps，the separation performance of the natural gradient algorithm，thestep size selection on the importance of convergence and steady-state error，this paper analyzes the convergence speed in step variationalgorithm，steady-state performance etc.

blind signal； separation technology； natural gradient algorithm；steady state performance； convergence speed

TN911.6

A

1674-6236（2014）15-0027-03

2014-04-09 稿件编号：201404095

河南省科技攻关计划项目（122102210510）

李留青（1981—），女，河南驻马店人，讲师。研究方向：计算机应用。