基于可靠性的微网容量最优配置
2014-09-26陈江斌束洪春
王 晶,陈江斌,束洪春
(1.浙江工业大学 信息工程学院,浙江 杭州 310014;2.同济大学 电子与信息工程学院,上海 201804;3.昆明理工大学 电力工程学院,云南 昆明 650051)
0 引言
随着化石能源逐渐短缺和环境污染日益严重,利用清洁能源的分布式电源DG(Distributed Generation)被提上了日程,而微网能有效地整合各种DG、储能单元及负荷,是未来智能电网的重要组成部分[1-3]。独立微网规划设计阶段中DG的定容和选址是首要解决的问题。一般主要从负荷和DG这2个角度考虑[4]:负荷方面要保证供电可靠性和电能质量;DG方面考虑投资成本和电网稳定性等因素,确定其最优容量和位置。对微网进行合理的优化配置可以有效地减少投资成本,提高负荷点的供电可靠性,保障电网的安全稳定运行,有利于节能减排[5-6],故逐渐受到多国政府和学者们的重视。
目前,国内外一些学者已对微网容量优化配置进行了相关研究,并取得了一些理论成果。文献[7]考虑系统的可靠性指标,并以部署和热补偿成本最低为优化目标,利用模拟退火法进行求解,确定了微源的最优安装位置和容量,但对于每一节点配置微源的类型没有给出相应的结果;文献[8]提出蚁群算法确定DG的最优位置和安装容量,其在满足DG容量约束的条件下,以系统网损最小为目标寻求最优解,然而蚁群算法选择的参数多且不同参数对优化结果影响较大,容易导致求得的并不是最优解;文献[9]考虑风机和光伏的互补性,以系统可靠性为约束,建立了计及系统投资成本、运行维护成本等综合成本的经济模型,采用改进微分算法对独立微网容量优化配置进行求解,但没有考虑蓄电池充放电功率的约束,这会影响系统的可靠性指标;文献[10]考虑风机、光伏、燃气轮机等多种微源,并以经济成本、供电可靠性和环境效益作为优化目标,将混沌优化技术和遗传算法相结合,对独立运行微网系统容量进行优化配置,但没有进一步讨论微源选址的问题;文献[11]提出细菌觅食法对风/光/储混合微网电源进行优化配置,在已知各微源模型的基础上建立计及设备投资、运行维护、环保折算和燃料成本的优化目标,根据不同可靠性指标得到相应微源的最优配置方案,但未考虑独立微网中可能存在能量浪费的现象,缺乏对能量利用率的衡量。
本文针对风/光/储独立供电微网,在分析各微源功率模型的基础上,构建了微网的经济成本、供电可靠性、能量过剩率的优化目标函数,提出一种基于可靠性的微源优化配置方法,并将其应用于一个5节点孤岛系统中。算例分析表明,该方法不仅实现了对独立微网中微源容量的优化配置,而且确定了微源接入系统的最优位置,在保证优化后孤岛供电可靠性的同时,节省了经济成本。
1 风/光/储微网电源模型
本文建立的独立微网结构如图1所示,主要包括微网控制系统、DG和用电负荷三大部分。微网控制系统能统一管理其内部所有DG和负荷,DG包含风机、光伏和蓄电池3种。
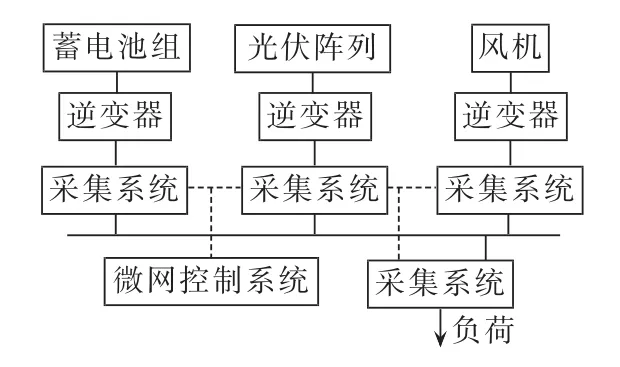
图1 独立微网示意图Fig.1 Schematic diagram of standalone microgrid
1.1 风力发电机模型
风机的输出功率随风速的变化而变化,本文采用威布尔(Weibull)分布对风速进行处理,其概率密度函数如下[12]:
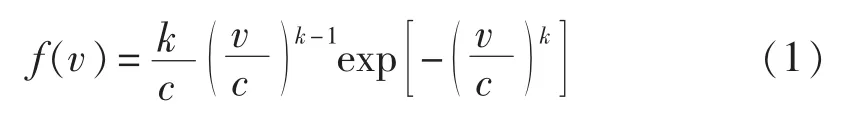
其中,v为风速;k和c为Weibull模型中的形状和尺度参数。
由此可建立风机输出功率和风速之间的近似关系,表示如下:
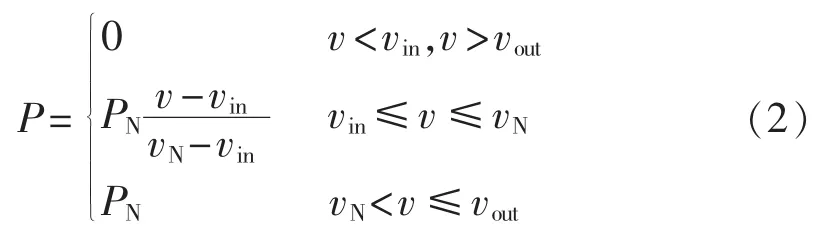
其中,vin、vN、vout分别为切入风速、额定风速、切出风速;PN为额定输出功率。
1.2 光伏阵列模型
光伏阵列的输出功率随光照强度和环境温度的变化而变化,本文采用Beta分布对光照进行处理,其概率密度函数如下[13]:

其中,Γ为Gamma函数;α、β为Beta分布的2个形状参数,不同时间段内根据光照强度平均值和标准差求得;G、Gmax分别为测试时间段内太阳光照的实际强度和最大强度(W/m2)。
由此可建立光伏阵列输出功率模型如下[11]:
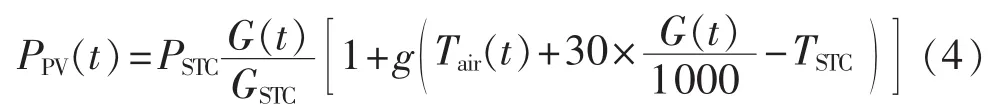
其中,PSTC为标准测试环境(STC)下的最大测试功率;GSTC为标准条件下的光照强度,取1000 W/m2;G(t)为第t小时太阳光照的实际强度;g为功率温度系数(通常取-0.004 5/℃);TSTC为参考温度(一般取 25℃);Tair(t)为第 t小时的环境温度。
1.3 蓄电池模型
a.荷电状态 SOC(State Of Charge)。
蓄电池荷电状态是反映蓄电池剩余电量占其总容量比例的参数,定义为[14]:

其中,Cbat为蓄电池总容量(A·h);Cnet为蓄电池剩余容量(A·h)。
考虑蓄电池的自放电和充放电,可得前后两时间段蓄电池荷电状态的关系,表示如下[15]:

其中,Ibat(t)为第 t小时充放电电流(大于0表示充电,小于 0 表示放电);Pbat(t)为第 t小时充放电功率;Ubat(t)为蓄电池端电压;σ(t)为自放电率,每小时取 0.01%;Δt为步长;Nbat为蓄电池的数量;η(t)为充放电效率,表示如下[16]:

显然,在一定的充电电流下,蓄电池的充电效率随着SOC的上升而下降,而放电效率则视为1。
b.端电压模型。
蓄电池端电压可由带内阻的电压源等效模型表示[17]:
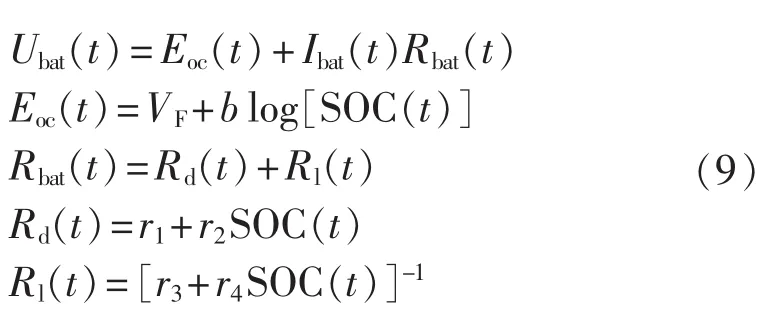
其中,Eoc(t)为蓄电池开路电压;Rbat(t)为内阻,包括电解质电阻 Rd(t)和电解液电阻 Rl(t);VF、b、r1、r2、r3、r4为经验系数,在充电和放电模式下取值见文献[17]。
2 优化配置模型
2.1 目标函数
本文建立了含有风力发电机、光伏阵列、蓄电池储能装置的独立供电微网容量优化配置模型,主要将设备投资成本、运行维护费用、蓄电池重置费用以及系统的能量过剩率EER(Energy Excess Rate)和负载供电率 RLPS(Rate of Load Power Supply)计入到目标函数中。优化目的是使系统在满足可靠性的前提下,等值年投资费用最低。目标函数如下:
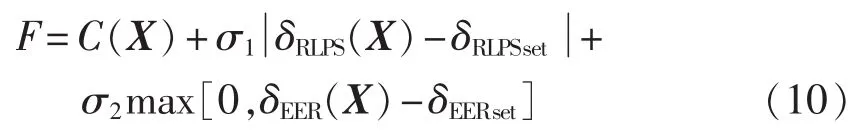
其中,C(X)为微源配置成本;δRLPS(X)、δEER(X)分别为系统实际的负载供电率和能量过剩率;δRLPSset、δEERset分别为设定的负载供电率和能量过剩率;σ1、σ2分别为惩罚因子,其随违反约束程度分段取值。
2.1.1 成本函数
成本函数中主要包括设备的投资成本、运行维护费用和蓄电池的重置费用,表示如下:

其中,N 为电源种类;X= [x1,x2,…,xN]为优化变量,为风/光/储数量;xi为第i种电源的配置数量;CAfi为第i种电源等年值设备投资成本;CAmi为第i种微源的年运行维护费用;CArep为蓄电池年均重置成本。
a.设备年投资成本。
微源的装机成本与具体项目密切相关[18]:

其中,Cbd为装机成本;α为折现率;Y为微源服役年限;δCRF为资金回收率 CRF(Capital Recovery Factor),表达式如下:

b.运行维护费用。
运行维护费用表示如下:
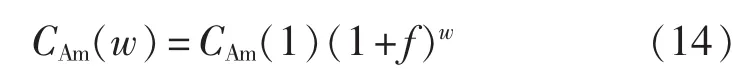
其中,CAm(1)为第 1 年的运行维护费用;CAm(w)为第w年的运行维护费用;f为全年通货膨胀率。
c.蓄电池重置费用。
蓄电池的寿命与项目年限相比通常比较小,因此需考虑其重置费用,计算表达式如下[19]:
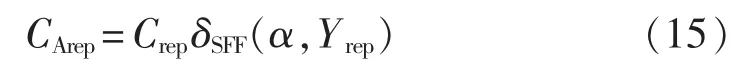
其中,Crep为重置成本;Yrep为蓄电池重置寿命;δSFF为偿债因子,其表达式如式(16)所示。

2.1.2 可靠性指标
本文采用负载供电率对系统的可靠性进行评价,负载供电率表示评估期内系统能满足负荷需求的概率,即:

其中,T为评估时间;Pload(t)为第 t小时系统总的负荷功率;Ploss(t)为第 t小时负荷失电的功率。
显然,微网系统的可靠性越高其负载供电率越大。
2.1.3 能量过剩率
独立微网存在能量浪费的现象,本文通过能量过剩率来衡量系统能量的利用率,定义为评估时间内系统浪费的能量除以系统总负荷,即[20]:
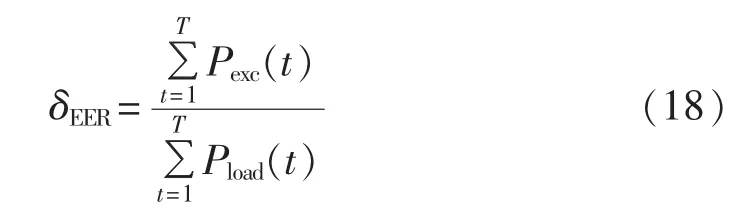
其中,Pexc(t)为第t小时系统过剩的功率。
显然,能量利用率越高,对应的系统能量过剩率就越低。
2.2 约束条件
2.2.1 数量约束

其中,NWGmax、NPVmax、Nbatmax分别为最大可安装的风机台数、光伏电池块数和蓄电池单元组数;N为自然数集合。
2.2.2 负载供电率和能量过剩率约束

如式(10)中,负载供电率以绝对值形式引入,表示系统实际的可靠性必须等于设定的要求;而能量过剩率以取较大值的形式引入,表示系统实际的能量过剩率只需小于设定值即可。
2.2.3 蓄电池电量和功率约束
为了确保蓄电池的寿命和运行的安全可靠性,通常需要考虑蓄电池在充放电过程中的约束条件。
a.荷电状态的约束。
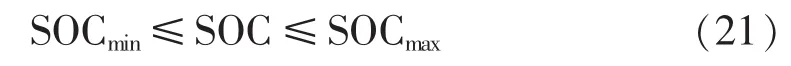
其中,SOCmin和SOCmax分别为蓄电池荷电状态的上、下限,一般取 SOCmin=0.2,SOCmax=1。
b.充放电功率的约束。
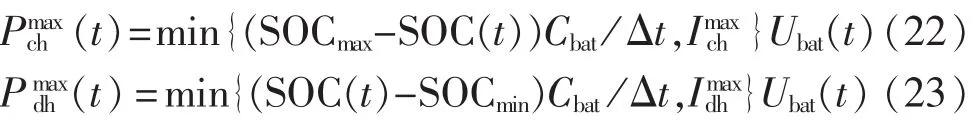
其中,Pmaxch(t)、Pmaxdh(t)分别为第 t小时蓄电池允许的最大充电功率和放电功率;Imaxch、Imaxdh分别为蓄电池允许的最大可充、放电电流,一般取额定容量的20%。
3 微网容量最优配置
3.1 系统负载供电率和能量过剩率的计算
考虑风速和光照强度的随机性与波动性,本文设计了4种不同情况(对应图2中子程序A—D),将一年划分为8 760 h,并假设风机和光伏阵列的输出功率在1 h内恒定,依据各微源的数学模型计算第t小时风机和光伏的总发电量以及系统净负荷:
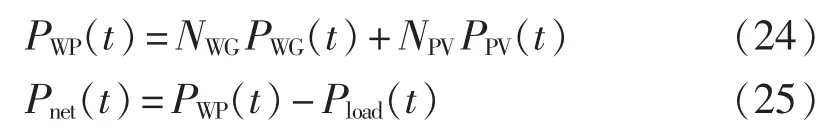
其中,NWG、NPV分别为风机和光伏电池的数量;PWG(t)、PPV(t)分别为风机和光伏阵列第 t小时的输出功率;PWP(t)为第t小时风机和光伏的总发电量;Pnet(t)为第 t小时系统净负荷。
A.若 0<Pnet(t)<Pmaxch(t),蓄电池按式(7)充电。
B.若-Pmaxdh(t)<Pnet(t)≤0,蓄电池按式(7)放电。
C.若 Pnet(t)≥Pmaxch(t),以最大功率给蓄电池充电但能量仍有多余,过剩功率Pexc(t)为:

D.若 Pnet(t) ≤-Pmaxdh(t),蓄电池以最大功率进行放电仍无法满足负荷的需求,失电功率Ploss(t)为:
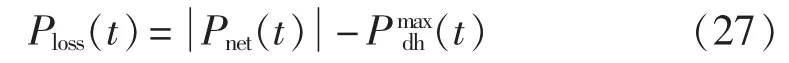
在得到各时间段内系统的失电功率Ploss(t)和过剩功率 Pexc(t)后,根据式(17)、(18)可计算得到负载供电率和能量过剩率。

图2 改进PSO微网容量优化配置流程Fig.2 Flowchart of improved PSO for microgrid capacity configuration optimization
3.2 微源容量的合理配置
3.2.1 系统平均停电频率
在求得微网中分布式电源总容量后,本文通过计算不同情况下系统平均停电频率(SAIFI)指标将其合理地配置到系统中不同的节点处。微源布址于微网的不同节点,考虑线路可靠性指标λ(次/(km·a))以及各负荷节点与微源间的距离,每个节点的供电可靠性程度都将发生改变。
对于m个串联可修复元件,其等效可靠性为[21]:

其中,λi为第i条线路的可靠性指标。
对于m个并联可修复元件,其等效可靠性为[21]:

基于元件失效影响,系统中某负荷节点只有当布址于本地的微源失效,并且由其他可能供电的途径发生中断,此负荷才会发生停电故障。根据微源接入的位置、容量和系统结构,可依次求得每个节点由于线路故障而导致断电的概率,从而得到系统平均停电频率指标[22]:

其中,NL为微网中负荷点的数量;Ni为连接带负荷节点i的用户数量。
3.2.2 微源容量合理配置准则
孤岛中每个节点负荷的大小不尽相同,选择微源布址于该节点时,不能无约束地任意选择容量。本文通过以下准则确定负荷节点微源的容量。
选择系统中可能布址微源的节点,每个节点配置微源的容量由下式确定:
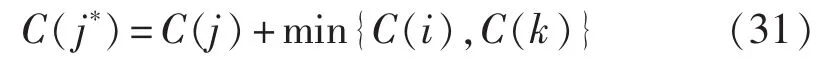
其中,C(j)为节点 j处负荷的大小;C(i)、C(k)分别为与节点 j相邻的节点 i、k处负荷的大小;C(j*)为节点j处应配置微源的容量。
当运用上述准则进行节点微源容量的选择时可能出现以下2种情况(分别对应图2中Ⅰ和Ⅱ):
Ⅰ.若∑C(n*)≤Csys,则将剩余的微源布址在离系统最大负荷最近的节点处,其中n为系统中选择布址微源的节点,Csys为系统所需的微源容量;
Ⅱ.若∑C(n*)>Csys,则微源按照相应节点负荷的大小布址,并将多余的容量布址在较大负荷处。
确定负荷节点微源容量后,以系统平均停电频率指标最小为目标确定微源接入系统的最优位置。
3.3 粒子群优化算法配置流程
风/光/储独立供电微网优化配置是一个在满足可靠性条件下的非线性寻优问题,其中约束条件(如可靠性、能量过剩率等)相比其他优化问题而言较多。若采用基本的粒子群优化(PSO)算法容易出现早熟和局部收敛等情况。因此,本文采用线性递减惯性权重的PSO算法(下文简称改进PSO算法),对目标函数进行直接搜索[23-24]。
基于PSO算法的微网容量优化配置主要分四大步骤(见图2):① 输入优化配置所需的一些基本数据,并随机初始化一群粒子;② 对每个粒子进行仿真,计算得到各自的负载供电率和能量过剩率;③采用改进的PSO算法确定微源的最优容量;④通过遍历的方法对微源容量进行合理的配置,确定其接入系统的最优位置。
4 算例分析
采用本文提出的优化配置策略对图3所示的5节点孤岛系统进行优化配置。其中,节点1—5所带的负荷数量分别为 100、300、450、50 和 100 户,各微源与当地负荷之间的线距离均为30 m,假设在这5个节点中需选出3个节点配置DG。微网中参数为:风机,额定功率10 kW,切入风速3 m/s,额定风速11 m/s,切出风速25 m/s,安装成本205 088元/台,运行维护成本 1910元/(台·a);光伏电池,开路电压30.8 V,短路电流 8.7 A,最大功率电流 8.16 A,最大功率电压24.5 V,安装成本3 446元/块,运行维护成本 13 元/(块·a);蓄电池,额定容量 100 A·h,电压 12 V,重置成本1 148元/块,安装成本1 276元/块,寿命 5 a,运行维护成本 13 元/(块·a)。 由风速和光照强度的分布函数,利用HOMER软件仿真得到微网所在地年气象数据(包括风速、光照强度和环境温度)如图4所示,年负荷曲线如图5所示。仿真时间为1 a,最小时间段为1 h,粒子种群大小为40,迭代次数为 100。
4.1 经济性分析
风/光/储独立微网能量过剩率 δEERset均设为100%,供电概率δRLPSset分别设定为100%、99%、98%的情况,微网电源优化结果如表1所示。
优化结果中能量过剩率δEER明显低于设定的100%,这表明风机、光伏电池、蓄电池三者之间找到了功率平衡点。在满足相同负荷需求的情况下,当风机和光伏电池能量过剩时给蓄电池充电,不足时蓄电池进行放电,有效地降低了微网的年投资成本。但由于风机、光伏电池、蓄电池成本偏高,因此寻优所得等值年投资费用仍远高于从电网的购电成本,以目前的市场价格而言是不经济的。但对于一些大电网无法送电的岛屿、边远军哨所等特殊场合,不失为合适的选择,且随着技术的进步,风/光/储独立微网的经济性、节能减排功能将会得到体现。

图3 5节点孤岛系统Fig.3 Islanded five-bus system

图4 微网所在地气象数据Fig.4 Meteorological data of microgrid location

图5 年小时平均负荷曲线Fig.5 Hourly average loads of microgrid for a year

表1 微源容量优化结果Tab.1 Optimization results of microsource capacity
4.2 可靠性对配置成本的影响
根据图2的流程,在设定相同的δEERset前提下,分别计算不同的可靠性指标δRLPS对方案年投资成本的影响,关系曲线如图6所示。
由结果分析可知:可靠性指标对经济性有重要的影响,可靠性设置得越高则微网的年投资费用相对就越高,经济成本随着可靠性的增加而增长。特别地,当可靠性指标在99%~100%变化时,微网的年投资成本变化相对较大,这说明高要求的供电可靠性将会导致经济成本的迅速上升。因此,设定合理的可靠性指标能有效降低电源的冗余投资。
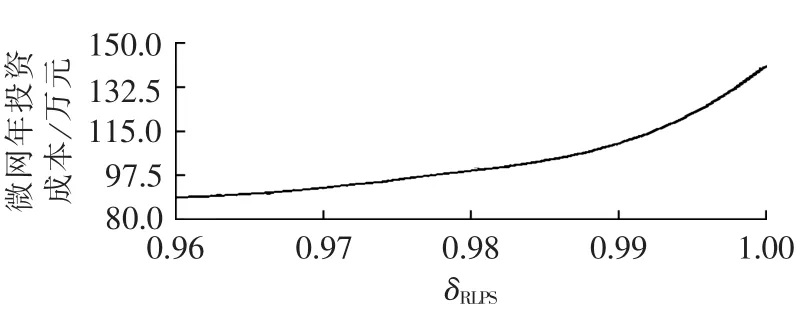
图6 供电可靠性与年投资成本的关系Fig.6 Relationship between power supply reliability and annual cost
4.3 可靠性指标与能量过剩率的关系
分别计算以下2种情况。
a.在能量过剩率δEERset为100%的前提下,计算可靠性指标δRLPS和能量过剩率δEER的关系,见图7。
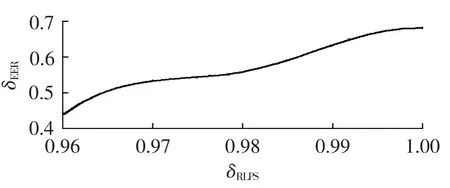
图7 可靠性指标与能量过剩率的关系Fig.7 Relationship between reliability index and energy excess rate
关系曲线表明能量过剩率随着可靠性指标设定的降低而逐渐递减,说明在供电可靠性放宽的条件下,系统可以在满足可靠性的同时减少微源的数量,从而降低年投资费用和能量的浪费。
b.可靠性指标δRLPSset设定为99%的前提下,计算在设置不同能量过剩率的条件下,其对可靠性指标δRLPS的影响,如图8所示。

图8 能量过剩率对可靠性指标的影响Fig.8 Impact of energy excess rate on reliability index
由图分析可知,当能量过剩率δEERset设置较大时,优化结果δRLPS始终等于期望值0.99,说明系统总能满足设定可靠性指标的要求,此时能量过剩率对可靠性不产生影响,即系统既能满足可靠性的要求,也能使能量过剩率在设定的范围内;而当δEERset逐渐减小到0.2附近时,发现求得的可靠性指标将小于设定值,说明系统已无法满足可靠性,以牺牲可靠性来满足能量过剩率的要求;当δEERset继续减小,δRLPS将迅速减小,系统可靠性急剧降低。
上述分析说明可靠性指标与能量过剩率之间存在矛盾性:可靠性指标希望系统每时每刻都能满足负荷的需求,而能量过剩率则希望分布式电源输出的功率每时每刻不要有余,即理想情况为DG每时每刻满足负荷的需求且无能量浪费,一般情况无法达到。因此,决策者可根据实际系统设计的要求,在PSO算法寻优中选择相应目标的微网设计方案。
4.4 微源容量配置分析
对图3所示的系统,设计2种情况。其中线路长度分别如下。
情况 1:l1=l2=…=l8=3 km。
情况 2:l1=l2=l3=2 km,l3=l4=l5=3 km,l7=l8=4 km。
遍历系统中所有可能的情况,可以得到2种情况下微源布址在不同节点对应的系统平均停电频率,如表2所示。

表2 微源布址节点与SAIFI的关系Tab.2 Relationship between microsource site node and SAIFI
当微源按本文提出的准则确定节点容量时,上述2种情况下均为电源布址在节点 2、3、5时δSAIFI最小。因此,节点2、3、5为微源接入系统的最优位置。同时分析微源布址在不同节点时δSAIFI值的大小得到如下结论。
a.当节点3不布址微源时,系统的δSAIFI均偏高,因为节点3处对应的负荷最大,说明对于独立供电微网而言,为了降低由于线路故障而导致负荷断电的概率,首先应考虑在最大负荷处就地布址相应大小的微源,以保证重要负荷的供电可靠性。
b.微源布址在相同节点上时,情况2计算得到的δSAIFI普遍低于情况1,说明适当地缩短系统较大负荷之间的距离有利于降低由于线路故障而导致负荷断电的概率,从而提高负荷的供电可靠性。因此,在微网进行规划阶段时,应尽量缩短较大负荷之间的距离。
c.将微源布址于节点1、4、5等负荷相对较小的节点上时,系统对应的δSAIFI均比较大,而布址于节点2、3、5时δSAIFI最小。由此可见,将微源布址在系统较小负荷处将极大降低系统的供电可靠性;相反,接入系统最大负荷处可靠性将显著提高,验证了本文方法的有效性和正确性。
在确定微源最优布址节点后,本文按节点负荷的大小分配各微源的数量,节点3处负荷最大,则对应的风/光/储数量也就越多,其次是节点2和5,在δRLPSset=99%、δEERset=100%时配置结果如表3所示。

表3 节点配置风/光/储的数量Tab.3 Number of wind/photovoltaic/storage configured at node
4.5 改进PSO算法寻优过程分析
本文采用改进PSO算法对风/光/储微网容量进行优化配置,在设定δRLPSset=99%和δEERset=100%的相同条件下,其与标准PSO算法的收敛曲线如图9所示。结果表明:在刚开始寻优时,由于粒子随机初始化导致2种算法的适应度值均很高,但改进PSO算法在迭代大约20次后就收敛于全局最优,收敛速度明显加快。改进的PSO算法具有群体智能算法并行搜索、易跳出局部最小的优点,并且整个优化过程仅耗时55 s。
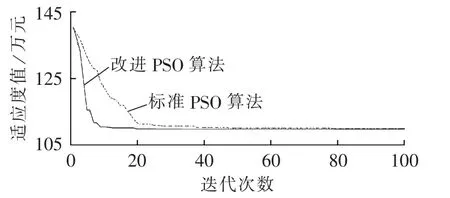
图9 标准PSO和改进PSO算法的计算结果Fig.9 Calculation results of standard and improved PSO algorithms
5 结论
本文提出一种基于可靠性的微网容量最优配置方法,通过仿真分析得出如下结论:
a.独立供电微网中风机、光伏、蓄电池三者之间能够找到功率平衡点,降低了年投资成本;
b.系统的可靠性是影响经济成本最重要的一个因素,经济成本随着可靠性的增加而增长,设定合理的可靠性指标能有效降低电源的冗余投资;
c.系统的可靠性指标与能量过剩率之间存在矛盾,两者不可能同时达到最优;
d.根据设定不同的可靠性指标和能量过剩率,改进PSO算法能够在保证系统供电可靠性的前提下,寻优得到相应的微网电源装机容量的最优配置方案,使经济成本最优;
e.通过系统平均停电频率指标,能有效地将微源布址于系统中负荷相对较大的节点,从而使整个系统由于线路故障而导致负荷断电的概率达到最小。
