考虑负荷分布变化的改进组合电力系统等效负荷持续曲线法

谈天夫，高 山，李海峰，罗建裕

（1.东南大学 电气工程学院，江苏 南京 210096；2.江苏省电力公司，江苏 南京 210014）

0 引言

电力网络对供电可靠性具有重要影响，网络传输能力的限制、网架的薄弱以及线路的随机故障都可能带来可靠性损失，所以在可靠性相关的评价中，网络是值得考虑的重要因素，而在电网规划过程中，网络影响更是不可避免的内容。系统可靠性指标评价是电力系统随机生产模拟的主要内容之一[1]，在随机生产模拟计算中考虑网络的影响，对其组合电力系统相关评价结果的合理性以及在电力系统运行、规划等方面的应用具有重要意义。

文献[2-5]通过仿真方法实现了组合电力系统的可靠性评价。通过仿真法可以方便地处理网络影响，但是可能会带来较高的计算负担。对于随机生产模拟解析算法，已提出基于负荷持续曲线[6-8]、序列运算[9]、时序负荷曲线[10]、负荷频率曲线[11-12]的众多理论和算法，现有方法多仅考虑发电机侧和负荷侧因素的影响，较少考虑网络因素。

利用关于负荷节点的组合电力系统有效负荷持续曲线（CMELDC）进行评价的随机生产模拟解析法[13-15]，可以对网络因素进行有效考虑，从而对发输电系统进行整体评价，但是由于该方法忽视了各负荷点具体负荷水平的变化对系统供电能力分配方式的影响，得到的可靠性评价结果可能存在较大偏差。本文针对CMELDC法中的这一不足，采用基于负荷比例分布的聚类方法和相关因子数据对各负荷之间的相互关系进行描述，并结合灵敏度方法获得各个负荷在其不同负荷区间内的等效发电机容量值分布，从而获得更加准确的评价结果。为便于表述，首先简介了CMELDC法的相关理论和方法，然后对该方法的不足和改进方法进行了讨论分析，最后基于所提方法对MRBTS系统和IEEE-RTS 79系统进行随机生产模拟计算，证明了所提方法的有效性。

1 CMELDC法

与其他随机生产模拟解析法相比，CMELDC法不仅考虑了发电机侧的影响，而且将输电线路的影响纳入了考虑范围。其核心思想是通过求取不同发电机和线路可用状态组合下的负荷点最大可达功率AP（Arrival Power）值，将发电机侧和网络侧的不同可用状态组合影响等效为连接在各个负荷点上的一组等效多状态机组，由这些等效多状态机组结合各负荷点的负荷持续曲线对系统的可靠性和经济性进行评价。其基本步骤如下。

a．形成系统状态集。

系统状态集反映了发电机的随机故障以及线路的随机断线影响，其中的每个状态对应一个发电机、线路可用状态组合。假设系统内有Nl条线路，形成的系统状态数量为NS，则对于加载i台机组后的某个状态j，其状态概率为：

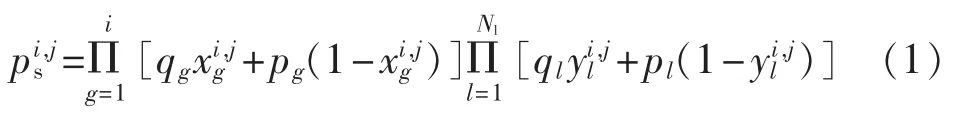
其中，pg、pl分别为发电机g和线路l发生故障的概率；qg=1-pg；ql=1-pl；xig，jє｛0，1｝、yli，jє｛0，1｝分别为加载i台机组后的系统状态j对应的发电机g和线路l的可用状态。

当发电机和线路数量较多时，状态数将会急剧增加，考虑到多元件同时发生故障的概率极小，可以据此对状态集进行精简，以减少状态数量。

b.计算系统状态集对应的最大AP值。

AP值反映了在一定的调度原则下，系统可用的发电机和线路对负荷侧的供电能力，其求解模型的目标函数如式（2）所示[13]：

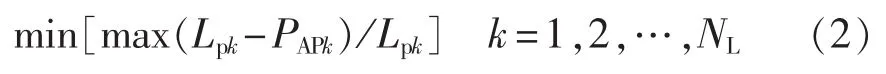
其中，PAPk为负荷节点k的AP值；Lpk为负荷节点k的峰值负荷；NL为负荷点数。可以看出，式（2）表示的目标函数体现了在平等对待各个负荷点的前提下尽量发挥系统供电能力的原则。

结合直流潮流方程和发电机出力约束、线路有功潮流约束，AP值的求解模型可以表示为：

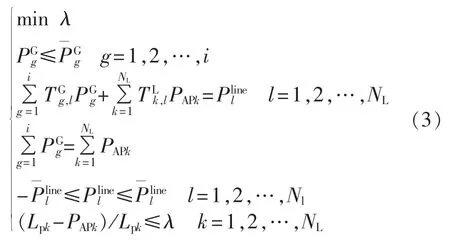
其中，PGg为发电机g的出力；为发电机g的出力上限；Plline为线路l传输的有功功率；为线路l传输有功功率上限；TGg，l、TLk，l分别为发电机 g 和负荷 k对线路 l有功功率的传递系数，TGg，l、TLk，l可由直流潮流计算获得；Nl为线路数；NL为负荷数；λ为无单位变量，表示（Lpk-PAPk）/Lpk的上界。

对于系统状态集中的每一个状态，都可以得到对应于所有负荷点的AP值，如此就在每个负荷点上形成了一个以AP值集合为输出容量的等效多状态发电机，其每个状态对应的概率为相应的系统状态概率，由等效多状态发电机容量可进一步得到等效发电机最大容量以及等效故障容量序列。

c.可靠性评价计算。

加载完所有发电机后，通过卷积得到负荷点k的等效负荷持续曲线为：

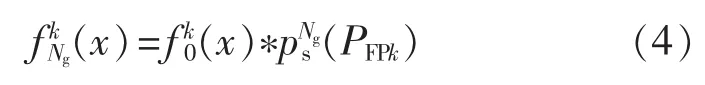
其中，“*”表示卷积运算；Ng为发电机总台数；fk0（x）为负荷点k的初始负荷持续曲线；x为该负荷点的负荷水平；PFPk为加载完所有发电机后负荷点k对应的等效故障容量序列；psNg（PFPk）为 PFPk对应的概率。由fNkg（x）可进一步计算得到各个负荷点及整个系统的可靠性等评价指标[13]。

2 基于聚类和灵敏度法的CMELDC改进算法

从式（2）、（3）可以看到，在 CMELDC 法中，对于同样的网络和发电机可用状态，AP值实际上主要受到各负荷点的峰值负荷比例影响。依据各负荷点的峰值负荷计算AP值，在一定程度上反映了供电能力的分配方式，但是由于各个负荷点的负荷存在着随机性，当负荷比例发生变化时，对应的供电能力分配方式会发生相应的变化，虽然这与负荷预测[16]、发电调度过程[17]等诸多因素相关，但仍可通过负荷比例来评估。以图1为例，设某个系统状态下由式（3）计算得到负荷点 1 —3（峰值负荷为 Lp1、Lp2、Lp3）的 AP值为 PAP1、PAP2、PAP3，当负荷点 3 的实际负荷值为 L′p3时，按峰值负荷比例计算的PAP3大于该负荷，系统出现冗余的供电能力，所以，此时按各点实际负荷比例计算，负荷 1、2 的 PAP1、PAP2可以提高至 P′AP1、P′AP2，PAP3变为P′AP3，可靠性水平与由PAP1—PAP3得到的相比，负荷1、2可靠性有所提高，而负荷3可靠性有所降低，系统整体可靠性有所提高。所以，仅通过峰值负荷比例得到的AP值无法反映各点负荷水平变化时系统供电能力分配发生改变带来的影响，由其得到的可靠性评价结果可能存在较大偏差，AP值计算应该考虑以实际的负荷比例为依据。

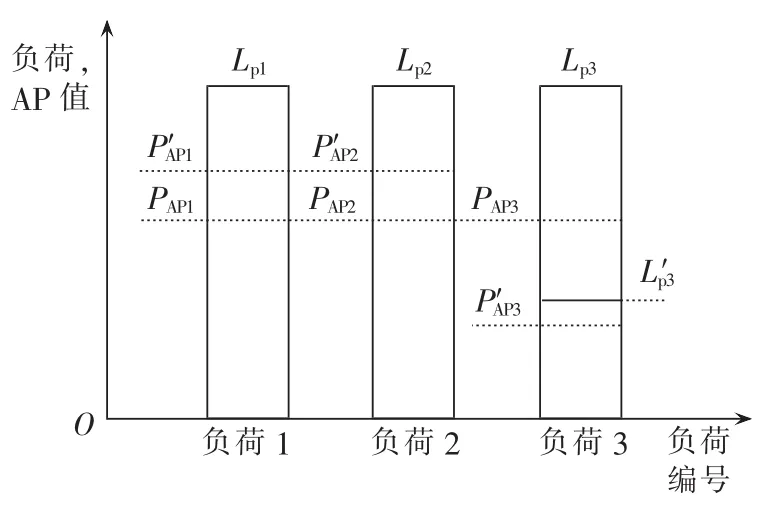
图1 负荷水平变化时的AP值变化Fig.1 AP variation along with load level change

2.1 基于聚类的改进

由于实际运行中可能发生的负荷比例状态数量庞大，不可能对其逐个进行AP值计算和可靠性评价。考虑到各个负荷点的负荷比例会在一定范围内随机分布，采用聚类方法对CMELDC法进行改进，通过获取负荷比例分布的一定数量的聚类中心，使其能考虑负荷变化的影响，具体方法如下。

设各负荷点的负荷样本集为S0，s0为S0中的一个采样，且 s0=[PL1PL2… PLNL]，PLk表示负荷点 k在采样s0中的负荷值。为了确保同样比例的负荷只有一种表达方式 通过将S，0转化为比例形式，可得到比例形式的样本集S′0，S0′与S0一一对应。通过聚类方式进一步得到S′0规模为的聚类中心集 S1，对于每一个 s′0єS′0，都有其对应的聚类中心s1єS1，通过S1可以在一定程度上反映负荷比例的分布。

显然，NS1越大，所能体现的负荷比例分布就越精确，但是相应的计算代价也会增加，所以需要选取一个合适的聚类中心规模。这里给出了一种获得NS1的方法：加载 i台发电机后，如果 s′0发生变化 Δs′0并且忽略网络约束的作用，则按照负荷比例分配的系统供电能力变化量为，如果设置容忍的AP值误差上界为，则可以通过聚类平均误差的条件来得到 NS1。 其中，NS0为S0的样本数，sw1为第w个聚类中心，nw为 s1w对应的样本数，s′0w，y为 s′0中 sw1对应的第 y个样本，‖·‖∞表示求向量的∞范数。文中聚类算法皆采用k-均值法，具体方法及步骤可见文献[18]。

因为一个负荷在处于不同负荷水平时可能面临不同的负荷比例分布，所以考虑采用相关因子概念来进一步描述各个负荷在不同负荷水平区域与S1中聚类中心的关联。

设负荷点k的负荷水平分为Nk段，其第m段的负荷区间为[PkL，m-1，PLk，m），定义其与 S1中第 n 个聚类中心sn1的相关度为：

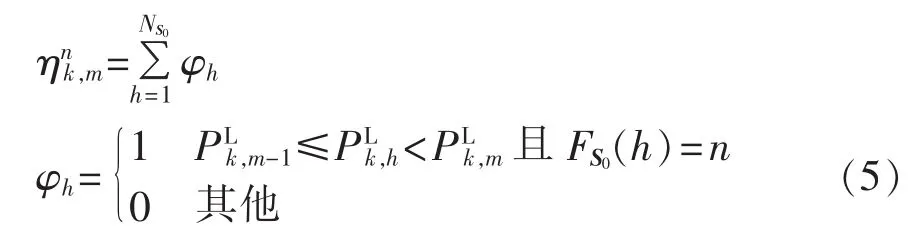
其中，NS0为 S0的样本数；PLk，h为负荷点 k在 S0第 h个采样中的值；FS′0（h）表示 S′0中第 h 个采样对应的S1中聚类中心序号；ηnk，m体现了负荷点的某一负荷区间所相关的负荷比例样本在sn1处的聚类归属情况，ηnk，m越大，说明该负荷区间的相关样本与sn1关系越密切。

进一步定义负荷点k第m个负荷段对S1中第n 个聚类中心的相关因子为。 则对负荷点k的所有负荷段和S1中的所有聚类中心进行上述计算，可以得到各个负荷段对S1的相关因子为：

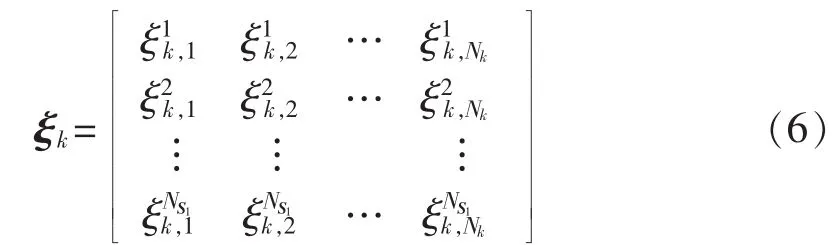
在CMELDC法中加入上述聚类中心集和相关因子概念，可以对负荷比例变化的影响进行反映，同时建立具体负荷水平与负荷比例分布之间的关联。由此，原算法需要进行以下调整。

a.首先，对每一个系统状态，求得S1中各个聚类中心对应的AP值，而不是仅仅求得峰值负荷对应的AP值。在第j个系统状态下，对于第n个聚类中心，其AP值求解模型（3）中相应约束变为：

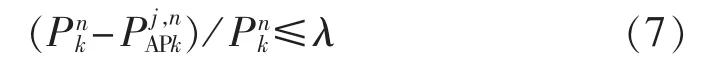
其中，Pkn为S1中第n个聚类中心对应第k个负荷的负荷水平（比例形式）；PAjP，nk为负荷点 k 对应第 j个系统状态、第n个聚类中心的AP值。

b.其次，在等效多状态机组形成过程中，将系统状态概率和相关因子概念结合，具体如下。

负荷点k连接的等效多状态发电机容量为：

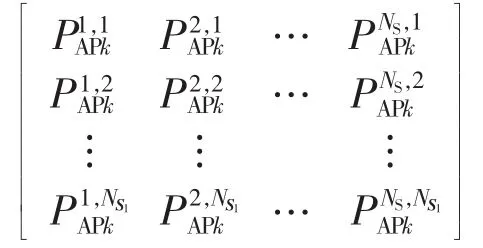
对于负荷点k的第m个负荷段，上述等效多状态发电机容量对应的概率为：

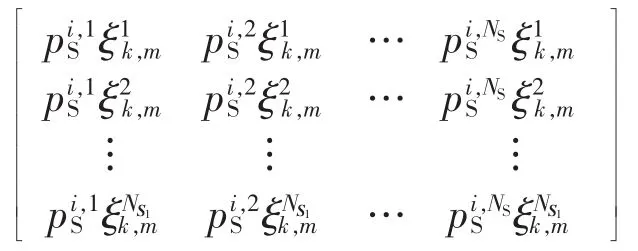
其中c.最后，各负荷点的可靠性评价指标需要逐个负荷段进行计算，其具体计算方法如下。为加载i台机组后的系统状态j的状态概率。

容量为个负荷段的可靠性损失，即电量不足期望值EENS（Expected Energy Not Served）和失负荷期望值LOLE（Loss Of Load Expected）分别为：的等效发电机对应的负荷点k第m

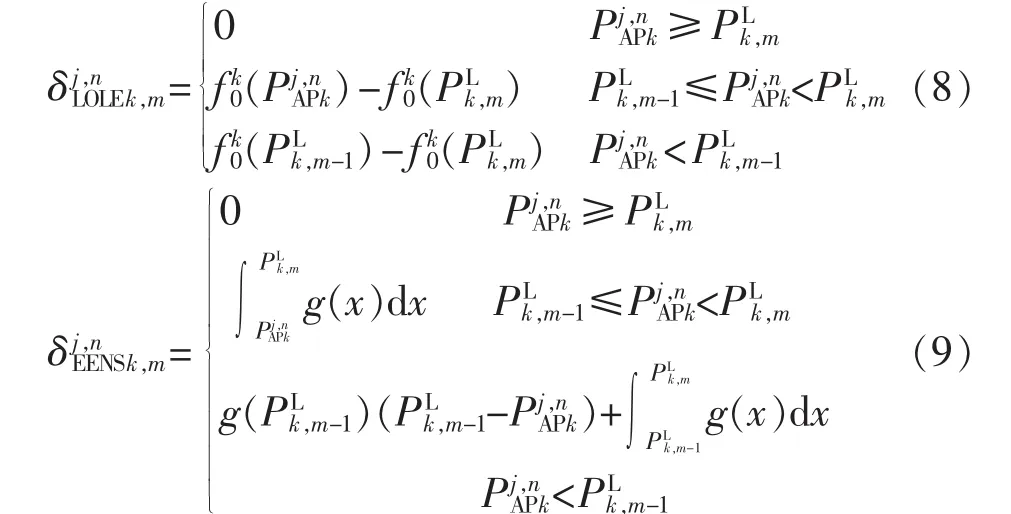
其中，g（x）=fk0（x）-fk0（PLk，m）。

各负荷点的可靠性评价指标为：

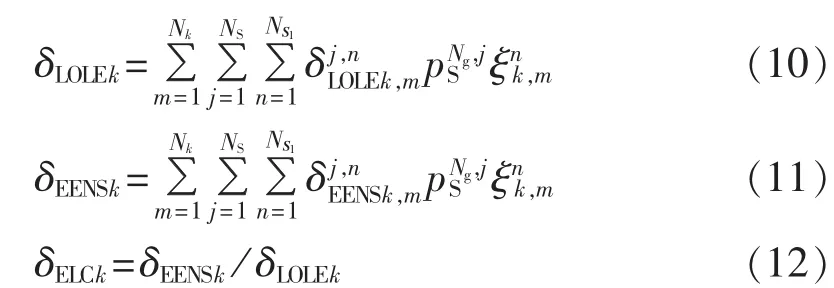
其中，δELCk为负荷切除期望值 ELC（Expected Load Curtailed）。

系统整体的可靠性指标为[15]：

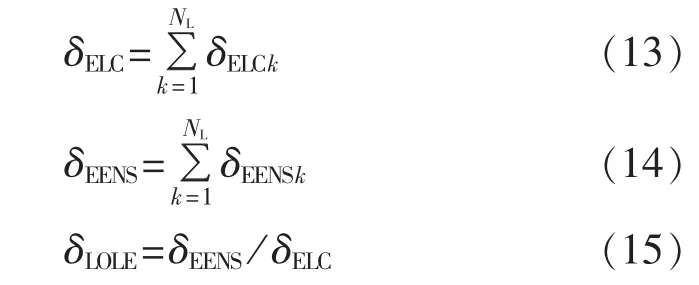
由于聚类中心的分布受到负荷样本分布的影响，当各个负荷点的负荷相关度较大时，其负荷样本（比例形式）分布会较为密集，需要的聚类中心数量也会较少；反之，则分布相对分散，可能需要更多的聚类中心。并且对于前一种情况，其实际负荷比例与负荷峰值比例差距可能相对较小，所以改进方法与原方法评价结果差距也会相对较小。

2.2 基于灵敏度的估算方法

当NS1较大时，S1对应的AP值计算造成的计算负担会明显增加，所以采用一种基于灵敏度的估算方法来获得S1对应的AP值解。

对于线性规划问题及其对偶规划问题

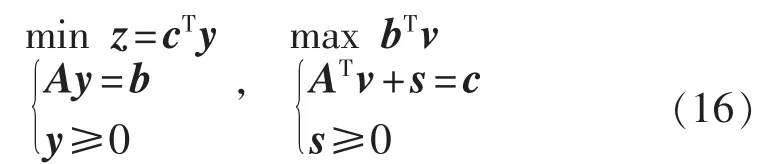
根据其最优条件，在其最优解（y*，v*，s*，z*）处对各变量求微分，可以得到[19]：

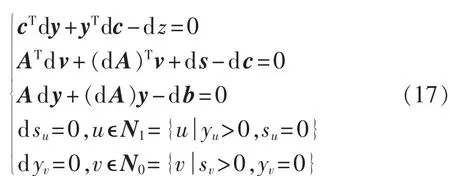
将约束改进后的式（3）写成式（16）中的标准形式，其各负荷点负荷水平的变化只对应于A中相应元素的变化，所以只需考虑y相对于A中元素的灵敏度，其求解如下：

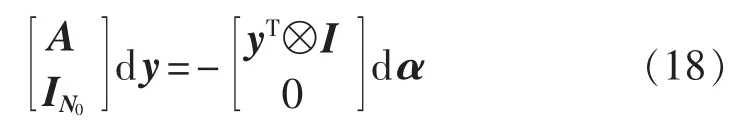
对聚类中心集S1采用灵敏度估算时，首先对S1进行再聚类，求得S1的规模为NS2的聚类中心集S2，显然，S2的规模比S1小很多；然后求出S2中各个聚类中心对应的AP值，以及AP值对应于各负荷点负荷水平的灵敏度；最后通过上述AP值和灵敏度对S1中聚类中心对应的AP值进行估算。NS2是一个较小的数值，可在1～20间取值，NS1越大，NS2取值也相应较大。

2.3 改进后的算法流程

当以可靠性评价为计算目标时，改进后的CMELDC法计算流程如图2所示。

3 算例

分别采用MRBTS系统和IEEE-RTS 79系统进行计算和分析。

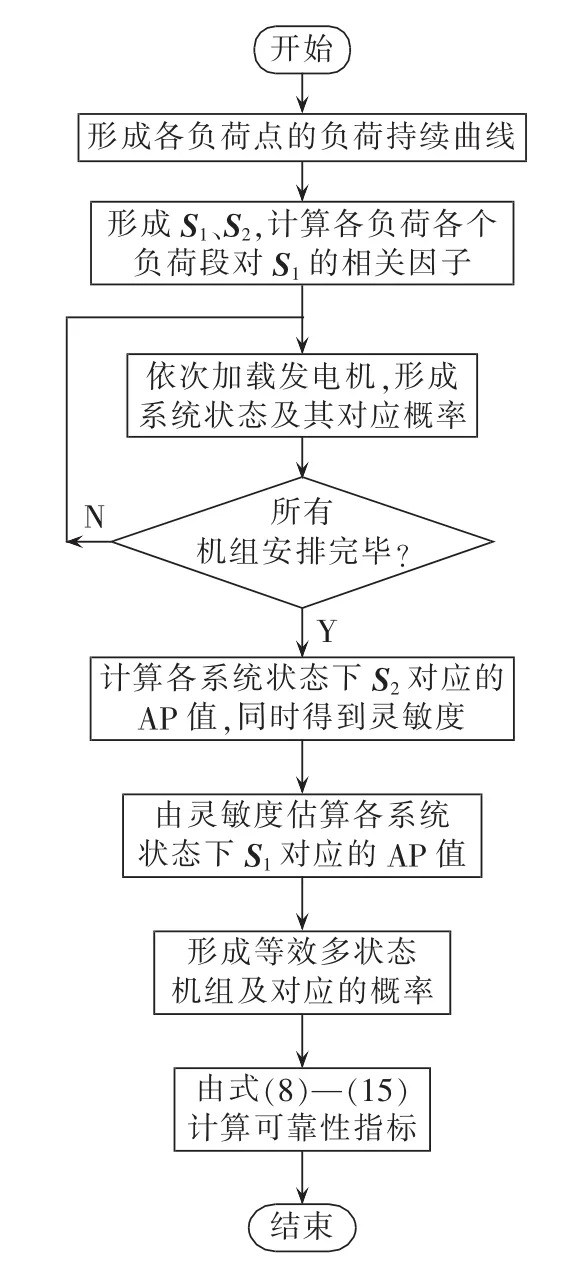
图2 改进CMELDC法流程Fig.2 Flowchart of improved CMELDC method

3.1 MRBTS系统算例

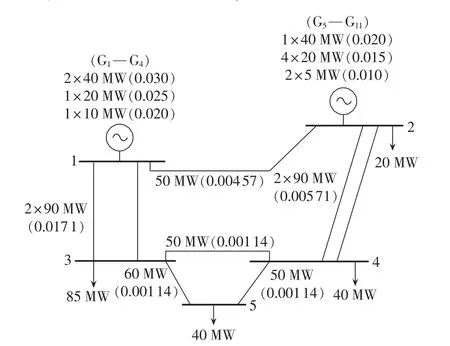
图3 MRBTS系统Fig.3 MRBTS system

采用文献[13]中的MRBTS系统，系统网络结构和发电机、负荷分布如图3所示（图中括号内数据表示强迫停运率），发电机优先顺序从高到低依次为G5、G6— G9、G10与 G11、G1与 G2、G3、G4，系统具体线路参数见文献[20]。分别基于2个不同的负荷样本进行计算，负荷样本1中系统各负荷节点的负荷根据图3中节点负荷峰值和文献[21]中年典型负荷数据调整得到，具体方法为对年典型负荷数据的24 h分布、周分布、年分布进行参数调整，形成各负荷节点有所差别的典型负荷数据，以避免采用同样的典型负荷数据导致各负荷节点负荷水平比例固定，结合各负荷节点的典型负荷数据和负荷峰值得到一年中各负荷节点小时负荷组合的时序样本（8736个），其部分负荷时序曲线如图4所示。负荷样本2中各负荷点负荷服从独立正态分布，分布参数如表1所示，参照正态分布的3σ（σ为负荷标准差）准则，设负荷标准差约为负荷峰值与期望值之差的1/3，通过随机采样获得各负荷节点负荷组合的10000个非时序样本。与负荷样本1相比，负荷样本2的各负荷之间具有更低的相关度，其负荷水平比例分布也更加分散。

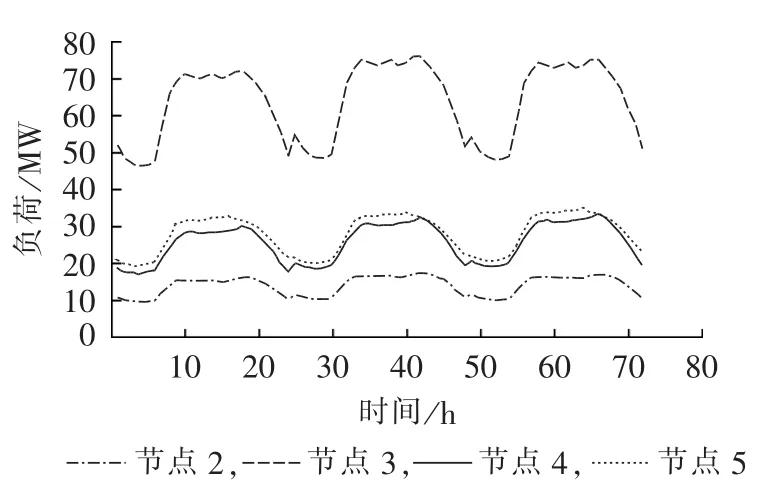
图4 负荷时序曲线Fig.4 Chronological load curves

表1 负荷分布参数Table 1 Parameters of load distribution

分别用CMELDC原算法、改进CMELDC法和蒙特卡罗模拟法进行试算，比较其可靠性评价结果。系统状态只考虑线路的单回故障，并且只考虑概率高于10-6的状态，总状态数为483。聚类参数负荷样本1取；负荷样本2取。各负荷点负荷水平分段步长为1 MW。在CPU2.8 GHz，内存2G的PC机上采用MATLAB编程计算。

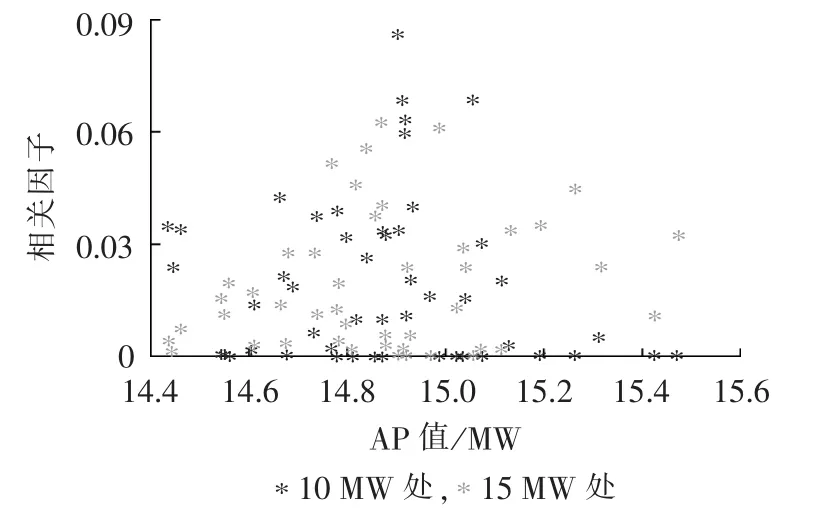
图5 节点2负荷水平15 MW和10 MW处AP值-相关因子分布Fig.5 AP-CF（Correlation Factor） distribution of node 2 for load level 15 MW and 10 MW

图5给出了负荷样本1的改进CMELDC法计算过程中，某一系统状态下节点2在负荷10 MW处以及15 MW处对应的AP值-相关因子分布，可以看到AP值在区间[14.5，15.5]MW内呈离散分布，并对应不同的相关因子值。由于图中AP值对应的是聚类中心集S1，其原始负荷样本集计算得到的AP值分布区间将更大。可以看到，15 MW处（浅色）的AP值-相关因子分布与10 MW处（深色）有明显的不同，对于相同的AP值水平（通常对应同一个聚类中心），两者的相关因子值具有明显的差别，以图中AP值15.04 MW对应的某个聚类中心为例，其在15 MW处对应的相关因子为0.02371，而在10 MW处对应的相关因子为0.01517，这反映了在不同的负荷水平下，可能实现的负荷水平比例分布的差别。同时，对某一负荷水平而言，由AP值-相关因子分布得到的可靠性指标应为一系列值的加权（对应相关因子）和。对于该负荷水平，不同的AP值可能意味着不同的可靠性损失情况，由此得到的可靠性指标是这些信息的综合，而如果采用单一的AP值进行评价，则无法反映其中的差别，可能导致较大的误差。

表2给出了对负荷样本1由3种方法得到的可靠性评价结果，相对于负荷样本2，负荷样本1各负荷的相关度较高。改进前后的CMELDC法在各项指标数值大小上各有参差，改进CMELDC法虽然在系统整体指标上较改进前有明显减小，但其得到的其余可靠性指标并未出现一致的减小，这是因为在更多地考虑系统供电能力分配调整后，一些节点的可靠性水平可能会有所提高，另一些则有所下降。与蒙特卡罗法结果比较，对于负荷样本1，改进前后的CMELDC法在各项指标上与其接近程度同样各有参差，虽然改进后可靠性指标值总体上更加接近，但并不显著。

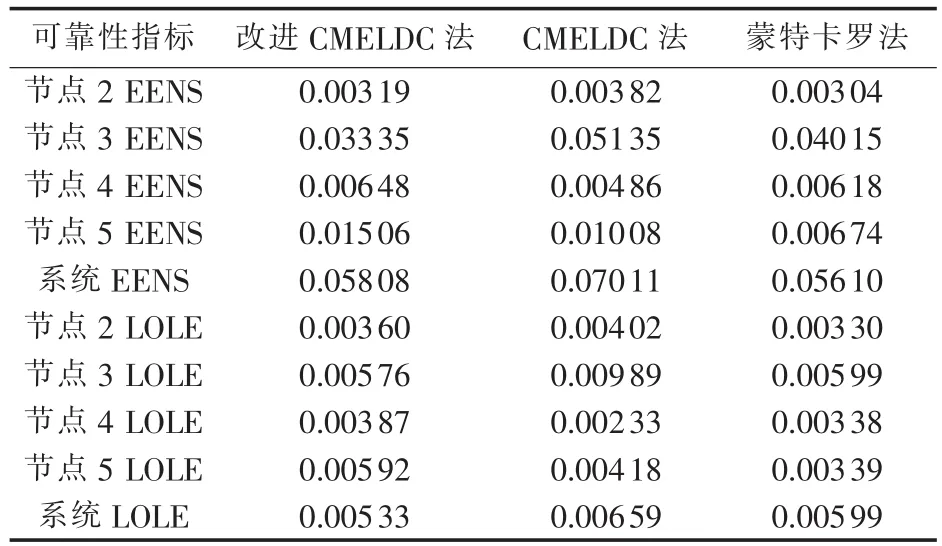
表2 可靠性指标计算结果比较Table 2 Comparison of calculated reliability indexes

表3给出了负荷样本2的相关可靠性评价结果。显然，负荷服从独立正态分布时，各负荷之间的相关度有明显降低，通过比较表2、表3可以看到，在负荷相关度降低的情况下，改进CMELDC法在计算结果准确度方面表现出了更明显的优势，其得到的结果更加接近蒙特卡罗法。

表3 负荷正态分布下的计算结果Table 3 Calculated results for loads with normal distribution

此外，与蒙特卡罗法结果比较，上述2个负荷样本均出现了节点可靠性指标计算结果偏差很大的现象，在后面的IEEE-RTS 79系统算例中亦如此。这主要由两方面因素导致：一方面是因为所用算例在蒙特卡罗法计算过程中，相同效果下切负荷选择存在一定的优先顺序；另一方面是因为虽然考虑了负荷水平变化对系统供电能力分配的影响，但仍有许多影响可靠性结果的细节被忽视，这同时也是系统总体指标存在偏差的主要原因。

对负荷样本1采用不同的ΔPAP得到不同的NS1，并改变NS2值进行计算，得到结果如表4所示。ΔPAP的减小与相应的S1规模的增大有助于更加准确地反映AP值分布，但达到一定规模以后影响就不再显著，结合表1中结果可以看到，对于上述算例，NS1达到50以上其造成的影响已较小。同时，通过比较 NS1为 10 与 100 时，NS2=2 与 NS2=NS1（S2=S1）2 种情况下的计算结果，可以看到灵敏度估算方法下的可靠性评价结果可以达到较为满意的精度。

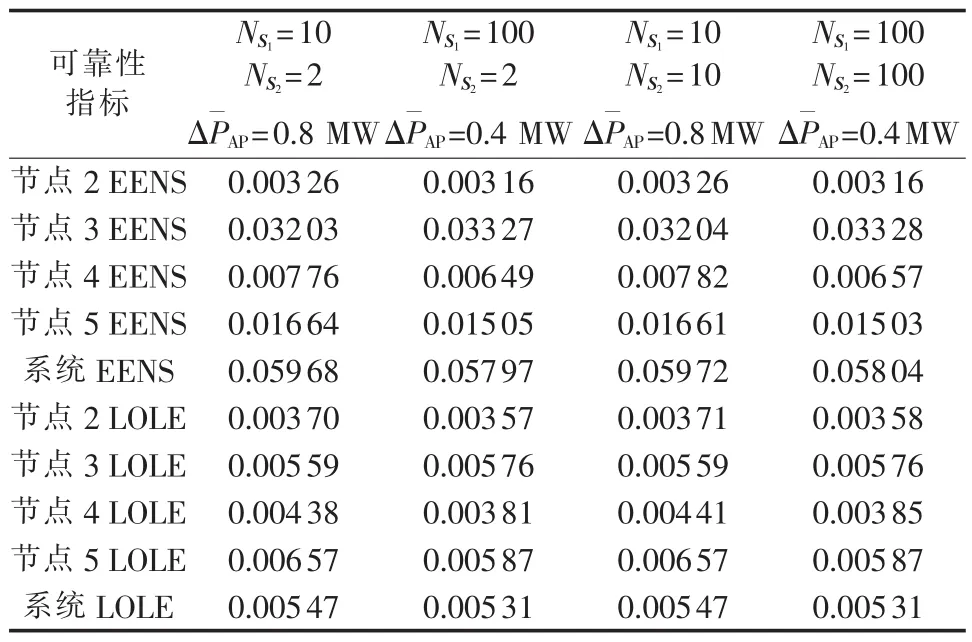
表4 不同聚类参数下的计算结果Table 4 Calculated results for different clustering parameters

以线路4-5断开一回、G9停运的系统状态为例，进一步对灵敏度法估算AP值的准确性进行分析，聚类参数取 ΔPAP=0.5 MW，NS1=50，NS2=2。对于S2中的一个聚类中心s2=[0.106 0.485 0.199 0.210]（比例形式），其各负荷点AP值为[0.250 1.139 0.468 0.493]（标幺值，基准为100 MW），由2.2节方法得到灵敏度矩阵为：

从而可以对S1中相关的聚类中心s1=[0.105 0.479 0.197 0.219]估算各负荷点AP值如下：

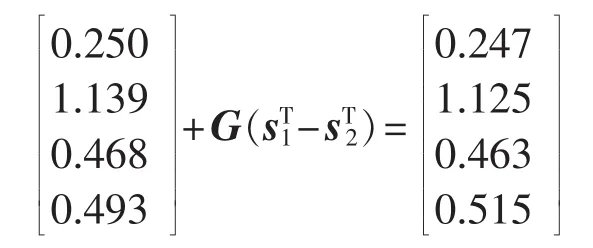
将S1中所有聚类中心的AP值估算结果与精确计算结果进行比较，得到各负荷点的AP值平均绝对百分误差分别为0.201%、0.065%、0.098%、0.233%，可见AP值估算结果具有较高精度。

在计算耗时方面，对于负荷样本1，CMELDC法为10 s，改进CMELDC法在NS1=50、NS2=2情况下为92 s，蒙特卡罗法采样次数为105时耗时215 s。可见由于需要考虑更多的负荷比例分布状态，即使采用了灵敏度估算的方法，计算耗时还是较原方法有较大增加，但是当系统较小时，相比蒙特卡罗法，改进CMELDC法的计算速度仍有一定优势。

3.2 IEEE-RTS 79系统算例

采用IEEE-RTS 79系统进行计算，该系统包含24个节点、34条支路、32台发电机和17个负荷点，其中支路7-8采用双回线路以防止N-1解列，各节点负荷服从独立正态分布，同样参照正态分布的3σ准则，设定各负荷点的负荷期望值为该点负荷峰值的3/4，标准差为该点负荷峰值的1/12，通过随机采样获得各负荷节点负荷组合的10000个非时序样本，包括负荷峰值在内的系统具体参数见文献[21]。为减小状态集规模，系统状态同样只考虑线路的单回故障，且只考虑概率高于10-6的状态，总状态数为16132，聚类参数取 ΔPAP=26 MW，NS1=1000，NS2=2，各负荷点负荷水平分段步长为1 MW。采用3种方法得到计算结果如表5所示。

由表5结果可以看到，在系统规模有所增大的情况下，与CMELDC原算法相比，改进CMELDC法仍然表现出计算结果准确度方面的优势，其所得结果更加接近蒙特卡罗法结果，尤其是在系统总体指标计算方面。同时，由于系统规模的增大，需考虑的系统状态显著增多，这使得改进CMELDC法的计算耗时达到了570 s，而蒙特卡罗法采样次数为2×105时耗时约600 s，可以推断，随着系统规模的增大，改进CMELDC法速度方面的优势有逐渐丧失的可能，因此，该方法更加适用于规模在一定范围内的系统，而系统状态的优选将进一步改善该方法的效率和适用性。

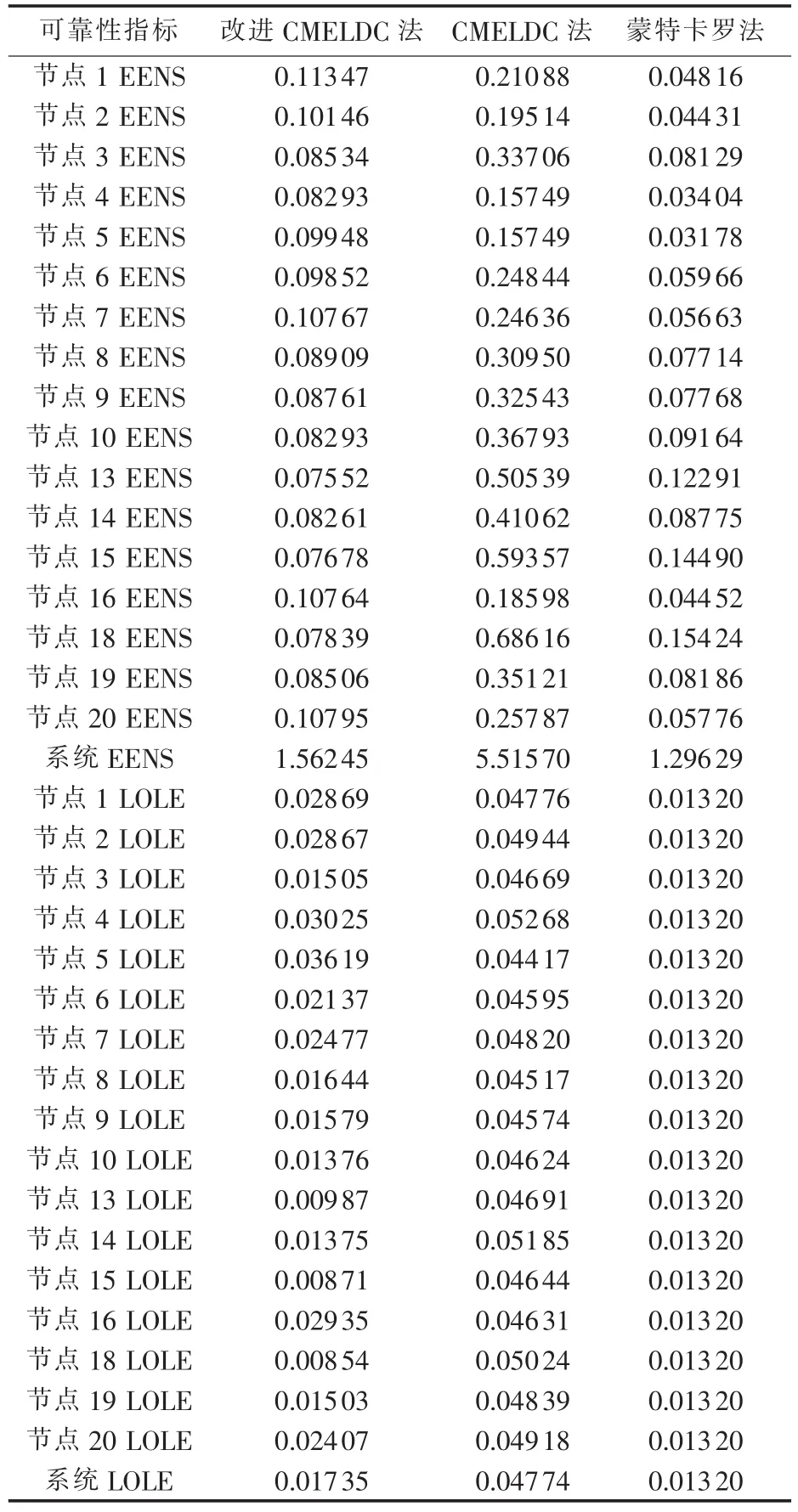
表5 IEEE-RTS 79系统计算结果Table 5 Calculated results for IEEE-RTS 79 system

4 结论

本文在CMELDC法基础上，采用基于聚类的方法对各负荷点负荷水平之间的相互关系进行描述，形成了反映不同负荷比例分布的聚类中心，并结合灵敏度方法对聚类中心处的AP值进行估算，从而形成连接于负荷处的等效多状态发电机，采用相关因子概念反映节点负荷水平与负荷比例分布间的关联，进而对系统的可靠性指标进行评价。算例表明，与原算法相比，改进后的算法在计算结果准确性方面有所提高，在负荷相关度较低的情况下其效果更加明显；同时，在一定的系统规模内，其在计算速度方面相比蒙特卡罗法具有较明显的优势，可应用于组合电力系统的可靠性评价计算及电网规划过程。

由于可靠性损失多发生于负荷较高的情况下，所以对高负荷区段内的负荷分布情况有针对性地加强描述，可有望进一步提高可靠性指标计算的准确性，并降低计算负担。同时，采用有效的系统状态优选方法，可有望减小涉及的系统状态集规模，从而提高计算效率和适用性。