马氏体转变(十九)

朱祖昌，杨弋涛，吴旭炜，王 洪

(1.上海工程技术大学，上海 201620; 2.上海大学，上海 200072;3.上海市机械制造工艺研究所有限公司，上海 200070)

马氏体转变(十九)

朱祖昌1，杨弋涛2，吴旭炜3，王 洪3

(1.上海工程技术大学，上海 201620; 2.上海大学，上海 200072;3.上海市机械制造工艺研究所有限公司，上海 200070)

7 钢中马氏体的硬度、强度和韧性

研究钢中马氏体的硬度、强度和韧性以及影响因素一直是人们关注的课题。自从上世纪六十年代起至今已有很多文献发表［122-136］。1962 年 Morris Cohen［122］在“1962 H.M.Howe 纪念讲座”上发表“The strengthening of steel”报告中讲到，钢的强化的诠释早在Howe教授1922年去世后就开始。1926年Sauveur发表著名的论述马氏体的形成、特性和硬度的“盖洛普民意测验(Gallup Poll)”结果，对钢中马氏体高硬度成因的主要观点为:1)原子键合的强化或形成新的键合，如化合物一样;2)固溶强化;3)内部应变的点阵扭曲;4)形成尺寸细小的马氏体晶体;5)微细碳化物粒子的弥散强化。显然这是第一篇论述马氏体高硬度的论文，尽管当时一些冶金学家的有些观点并不很正确，但是已经揭示出实质原因。

在我们收集的论述钢中马氏体强化机制的最近论文中，大村孝仁等［123］的“A new approach for interpretation of strengthening mechanism of martensitic steel through characterization of local deformation behavior”(2006年)和森户茂一等［124］的“Three dimensional morphology of lath martensite in a medium carbon steel”(2013年)都阐明钢的板条马氏体强化主要原因为固溶强化、析出弥散强化、位错强化和马氏体板条三“阶层”组织(这是日本学者的称法，在国内称束、块和板条结构)引起的细粒强化四个方面。

现在，人们已经知道，钢中马氏体的强度和硬度主要决定于钢中奥氏体的含碳量，韧性主要决定于奥氏体晶粒细化、马氏体亚结构类型和板条束、块的尺寸大小。本文就钢中板条马氏体的强度、硬度和韧性着重进行分析。

7.1 马氏体的硬度

一般商用合金钢淬火态马氏体的最大硬度主要取决于奥氏体中的含碳量，合金元素不影响或很少影响其最大硬度数值。图7-1汇综表示许多碳钢和低合金钢的淬火态硬度和含碳量的关系［126-127］。对应于一定含碳量，测定的相应硬度在100 DPH(DPH为金刚钻锥形压头硬度值)波动范围内。实际上，有些研究者已经采用液氮冷却以减少残余奥氏体量。为作比较，我们将 Krauss［125］对4320钢渗碳和油淬的不同含C量部位相应测得的纳米硬度值也拼合于图7-1中，以点线表示。

图7 -1 一些碳钢和低合金钢中马氏体的淬火态硬度和含碳量的关系Fig.7-1 As-quenched hardness of martensite in some carbon steel and low alloy steel as a function of carbon content

由图可见:1)当含碳量为0.30%时，Bain和Paxton的细实线(B-P)数据，Jaffe和Gordon的虚线(J-G)数据以及Krauss的点线数据值同为600 DPH和≈56 HRC。以后随含碳量增加，三者差异增大，其中纳米硬度数据上升的陡度最大，在0.80%C和更高的含碳量的值将近70 HRC。同时，Krauss指出，4130钢淬火后得到的马氏体板条间在TEM暗场下存在呈亮线特征的残余奥氏体，为此，硬度曲线上的差异可以得到说明。注意，B-P线和J-G线外推至0%C时硬度值为240 DPH。

图7 -2 (a)、(b)淬火态和不同温度回火碳钢的硬度与含碳量的关系和(c)对马氏体硬度可能强化机制的说明Fig.7-2 (a)、(b)Relationship between hardness of carbon steel for as-quenched and tempered at different temperatures and carbon content(c)and accounting for the possible strengthening mechanisms on hardness of martensite

2)当含碳量≤0.40%时，三者曲线所示的硬度值均呈直线增加，当含碳量＞0.40%时，硬度上升幅度下降，这是由于随钢中奥氏体的含碳量增加，淬火组织中出现的残余奥氏体量不断增加的缘故。

J-G和B-P线在含碳量增加至0.9%时，硬度达最高值(对应为67.5 HRC(900 DPH)和65 HRC)，以后均出现下降，其中 J-G曲线下降段趋势与Litwinchuk等对Fe-C合金自奥氏体进行盐水淬火的硬度曲线［127］基本一致，为钢全部奥氏体化(奥氏体化温度＞Accm)后淬火得到的硬度值。同时可以推知，近于水平段曲线为过共析钢按正常工艺淬火获得的硬度值。

图7-2(a)表示淬火态和在不同温度回火碳钢的维氏硬度与含碳量的关系。也为便于比较，将图7-1中除去纳米淬火硬度后的曲线拼合一起［126-127］。由该图可以看出，原图中所定的高于0.5%C的淬火态硬度位于B-P曲线和J-G曲线中间，也就是说，原图中表示的高于0.5%C表示的的J-G曲线(虚线)部分是不正确的，应予删去。图7-2(b)为改正后的图。

试图说明图2所示的淬火态硬度和含碳量的关系与分析马氏体强化机制相联系的工作首先出现在Pickering论文128］中，本文将之列于图7-2(c)。作者指出，马氏体有效强化机制为:1)碳或氮的固溶强化;2)细小马氏体或板条;3)板条马氏体中的高密度位错;4)高碳透镜形马氏体中的孪晶界面阻碍位错移动;5)在回火和自回火组织结构中碳化物的析出;6)间隙溶解的碳或氮和位错的交互作用。H.Tsubakino［129］认为，这是 Pickering 作了估算定性说明图7-2(b)的情况，实际上，Pickering的说明是存在较大差异的。

下面是我们比较好地说明钢淬火态硬度和含碳量关系的分析:人们都已知道，低碳钢和低合金钢淬火至室温过程中，由于Ms点较高，C原子会发生重新分布，甚至形成碳化物(如Fe3C)后析出，从而引入析出强化，这一般称自回火。为了克服碳的重新再分布的影响，Cohen等通过对不同的含C量钢加入 Ni(对 0.02、0.23、0.40、0.59 和 0.82%C 分别加入 30.5、26.8、23.3、19.2 和 16.7%Ni)使 Ms降低至-35℃以获得碳不发生重新分布的孪晶片状马氏体。这些试样的0.6%流变应力与含碳量之间的关系曲线示于图7-3［125］，并延伸至100%马氏体处。这样求的流变应力与未时效和发生时效的马氏体的含碳量比较曲线示于图7-4［125］。Cohen等得到的马氏体强度与含C量之间呈立方根关系。但是，后来的分析表明两者呈平方根关系。归纳的未发生时效和发生时效马氏体强度σ0.2的方程式分别为(7-1)和(7-2)式 :

图7 -3 不同Ni、C含量的Fe-Ni-C合金流变强度与马氏体数量(并外推至100%)的关系Fig.7-3 Flow strength as a function of mrtensite content and extrapolation to 100%martensite in various Fe-Ni-C alloys

图7 -4 Fe-Ni-C合金马氏体流变强度在未时效和时效条件下与马氏体含碳量的关系(试验温度为0℃)Fig.7-4 Flow strength of martensite as a function of carbon content in Fe-Ni-C alloys under unaged and aged condition at tested temperature of 0℃

式(7-1)中第一项为无碳马氏体的流变应力，包括无碳bcc铁中位错移动的摩擦阻力69 MPa，Ni的固溶强化项138 MPa和马氏体亚结构强化项255 MPa。公式(7-2)中常数项对应于亚结构为0.25 μm的板条宽度的强化项。

图7-5［125］指出高于0.013%C 钢屈服强度(试样盐水淬火并保存于液氮中)与含碳量呈式(7-2)所示的平方根关系。相应≤0.013%C钢的低强度是由于其低淬透性形成非马氏体组织造成。对更低含碳量(至0.058%C)的含Ni或Mn增加淬透性的钢，Norstrom也发现其屈服强度与含碳量呈平方根关系(图 7-6)［125］。

图7 -5 低碳钢马氏体的屈服强度与含C量关系Fig.7-5 Yield strengths of low carbon martensitic as a function of carbon content

图7 -6 低碳Fe-C和Fe-Mn-C钢马氏体的屈服强度与含C量关系Fig.7-6 Yield strength of martensite as a function of carbon content for Fe-C and Fe-Mn-C low cabon

碳钢和低合金钢的Ms点高于室温，在淬火过程中不能遏制碳的扩散和碳化物的析出。Speich应用测定Fe-C马氏体淬火态的电阻对含碳量关系曲线说明示于图7-7［125］。它表明含高于0.2%C碳钢中，由于碳原子在马氏体八面体间隙位置的混乱分布，增加了电子散射，为此具有较高的斜率。相反，低于0.2%C的碳钢具有较低的斜率，证实了Speich提出的在0.18%C钢马氏体中几乎90%的碳原子偏聚于位错处，从而仅具有较低的电阻率。

图7 -7 淬火态Fe-C马氏体电阻率的斜率与含碳量的关系Fig.7-7 Slope of electrical resistivity as a function of carbon content for as-quenched Fe-C martensite

基于此，大村孝仁123］指出，遏制C再配分的无时效和存在时效条件下，不同含C量钢的屈服强度差值分别为:

另外，大村等还提出，钢的马氏体中位错密度约1010～1011/cm2，与强烈冷加工的位错密度相当。由于位错引起的屈服强度增加值为:

又按文献［123］，0.6%C以下 Fe-C合金的位错密度ρ与含碳量(ω)关系为:

由此可求得0%C和0.2%C合金的位错密度ρ0和 ρ0.20以及位错引起的屈服强度增加值 Δσd0和Δσd0.20分别为:

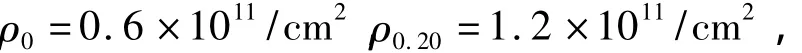
△σd0=156.2 MPa 和 Δσd0.20=220.84 MPa。

又按屈服强度/HV(≈3)近似计算成HV值相应为52 HV和73 HV。

图7 -8 Fe-C和Fe-Mn合金板条马氏体的屈服强度与晶粒直径D的关系Fig.7-8 Yield strength of plate martensite as a function of grain diameter D，for Fe-C and Fe-Mn alloys

大村还指出，细晶粒强化△σsg和Hall-Petch公式中Kg=25 MPa/m，以板条马氏体的束尺寸为10 μm 计算△σsg=250 MPa，可换算为83 HV。

这样可以求得0%C钢的HV值为:HV0=100+52+83=235，(其中100 HV为纯铁单晶的维氏硬度基值)，它与图7-2中0%C的约300 HV示值的差为65 HV，但与图7-1中0%C的240 DPH值相近。

对 0.2%C，先按上述可以求得 HV0.20=100+73+83=256，但图7-2上显示的值为500 HV，相比较的差值为244 HV。应归咎为C的固溶强化和细粒强化。又按图7-8相比较，Fe-C合金的ky比Fe-Mn合金的高2倍，为此HV0.20可修正为339 HV。但是，数值还比500 HV的差为161 HV，其中如果将C的固溶强化量按Cox数据计算，为137 MPa→46 HV，数值显然还是低很多。为此，这样的计算存在一定的问题。

我们按0%C 合金 HV0≈300 和 Δσs0.2%=1.8(ω(C))1/2，并将计算求得的 Δσs0.2%值换算成 HV值的方法，可以相应求得的 0.2、0.4、0.5 和 0.6%C钢的ΔHV值，以及计算HV列于下表7-1中，括号中数字为与图7-2(a)中数值的相差值。尽管以上计算结果与图7-2比较还存在一定的差值，但可以肯定的说，上述分析基本上能较好说明维氏硬度(HV)和含碳量(ω)之间关系的。

表1 按含碳量相应求得的ΔHV及计算HV值Table 1 The calculated ΔHV and HV values according to carbon content of steels

另外引人注意的是，不同含碳量钢淬火半马氏体区的硬度H1/2可以近似用下式计算:

式中ω(C)为碳的质量分数。H1/2值的确定对决定钢件淬透层深度可作参考。

7.2 马氏体的屈服强度

很多文献［125，128，130，132-133，135］根据强化机制分析列出与Hall-Petch公式相类似的方程式来表述钢中马氏体的屈服强度。我们将之汇总如下式:

式中:σy为屈服强度;σi为摩擦应力，主要为Peierls应力(即Peierls-Nabarro应力);σss为固溶强化项(包括间隙原子和代位式原子的固溶强化);σp为析出强化项;σd为位错强化项;σsg为亚晶粒界强化项，σt为晶体学织构强化项参量。以上这几项实际上为Hall-Petch公式中 σw项的扩展，Ky为屈服强度因子;d为粒界直径。

至今为止，很多研究努力将上述(7-5)式应用于对淬火马氏体和回火马氏体的强度进行阐明，但较完整的定量计算，并与实际测定值作比较的工作很少，本文将进行较系统全面的分析，并基于1993年Maropoules等［130］的工作作较深入的综述。

1)Peierls-Nabarro 应力 σi131］，又称摩擦应力，表示在完整晶体点阵中出现的一个位错的移动阻力，它为位错存在引起原子错排的错排能WAB对位错位置系数α的偏导数:

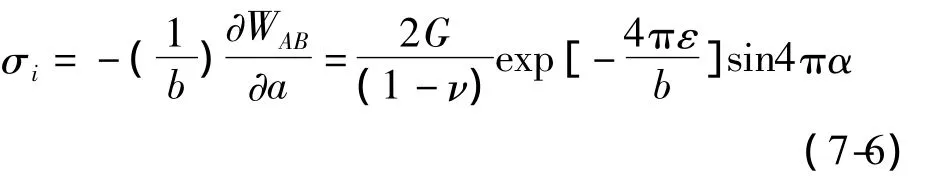
当d=b和ν=0.3时，

即σi=29.5 MPa，这计算值接近于实验的测定值13～55 MPa［130］。本文中取 41 MPa。

2)固溶强化项σss:σss应包括碳的和代位式原子的固溶强化。Maropoules等对C的固溶强化是这样考虑的:相应成分的 0.38C-0.22Si-0.45Mn-0.90Cr-0.73Mo-3.37Ni-0.02V-0.02Al-0.20Cu 钢，经预先正火和不同温度(830～916℃)加热淬火以及620℃附近温度回火处理后，相应基体含碳量 ～0.01%C的平衡值，这样按Cox的数据，C的固溶强化约为137 MPa。对淬火态的碳钢和低合金钢，按Cox的数据计算碳的固溶强化量明显偏低。

Maropoules等对代位式原子的固溶强化按Lacy等的工作采用强化参数方法进行计算，相应的贡献在上述热处理条件下认为相同。对不同元素的影响因子采用相加原则，这样，我们对代位式原子的固溶强化贡献相加数值和为128.99 MPa，适当考虑元素间相互作用后的结果为258 MPa。

3)析出强化项σp:按Frank-Read位错源启动的应力τ=Gb/2r和按位错绕过析出物的Orowan强化机制，析出强化阻力为τ=Gb/2r，设x为在位错滑移面上两个析出物粒子之间的平均间距(x=2r)时，τ=G b/x。Ashby改进原始的Orowan方程提出克服析出强化的临界分切应力(critical resolved shear stress)τ的 Ashby-Orowan关系式［130］为:

式中:D为一个平面上析出物交截直径平均值(μm);L是析出物外表面-外表面之间间距(μm)，并按下式的计算求得:L=D［(π/4f-1］，其中 f为析出物(如Fe3C等)体积分数。析出Fe3C时的理论体积分数按杠杆定律计算为5.37%。G为切变模量;r0为位错芯半径，一般r0=2b，b为布氏矢量(b=2.48 nm，计算公式中按 μm 计);1/1.8是 Kocks导得的系数，并设拉伸应力σp≈2τ。(7-9)式可写作为

另外也可以按 Hirsch和 Hamphreys改进的Orowan方程为

式中:ν为泊松比，K=0.81，r0=b代入后为下(7-11)式:

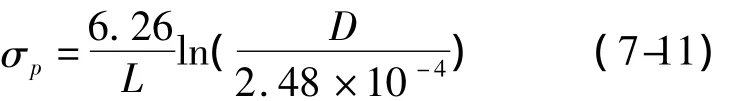
在Maropoules等工作中，上述(7-10)和(7-11)式计算值相差＜8%，均可适用。具体计算值列于表7-2的σB中。根据试验测定参数计算的值在(190～246)MPa范围。

4)位错强化项 σd:Bhadeshia等［135］提出，转变产生的形状改变不能进行弹性调整，会引起塑性变形，在母相和产物相中引入大量位错。位错密度会达到1010～1011/cm2，大致与强烈冷加工的相当。按Taylor方程式计算，σd=αGbρ，式中ρ为板条马氏体中的位错密度，文中根据列于下表的TEM测定值以及计算的σd值见下表7-2。切变模量G为8.31 GPa，b为布氏矢量(b=0.248 nm)，α为系数，按Roberts的结果α =0.88。注意，在有的文献中，α =0.3 或0.38 等，有点差异。

表7 -2 Maropoules等工作中一些参量测定值以及计算值Table 7-2 The examination and calculation data of some parameters in research of Maropoules et al

5)亚晶粒界强化项σsg:在板条马氏体三“阶层”组织中，束尺寸和板条尺寸会对屈服强度起影响。(现在大部分研究者认为，块的尺寸起主要影响，因为块之间的位向差别较大，板条之间位向差别较小，起的强化作用小)。束的尺寸d采用夏氏冲击试样断口中最小的准介理小平面尺寸表示，由SEM测定，Maropoules等的工作中由150个数据求得的平均值d(以mm计)，然后按Whiteman的方程进行计算:σsg=28。

6)加工硬化引起的贡献项σw:根据屈服拉伸的应力应变曲线进行估算，为弹性屈服极限和应变为0.002(0.2%)强度之间差值，约为 55 ～75 MPa，这儿取65 MPa。

这些贡献项全部计算后按下述进行结果的处理:

1)求取 σc项，σc=σi+σss+σw=41+(137+258)+65=501 MPa;

2)求取 σB=σc+σsg+σps=501+(412.7 ～502)+(190～246)=(1104～1249)MPa;

3)以 σd=σA;

4)对σA和σB两项求取均方根和σrms=(σA2+σB

2)1/2。我们对Maropoules等［130］的工作中的20个试样求取的σrms(计算与原Maropoules等的工作稍有不同)和实际测定的σ0.2全部列于表7-2中，相应误差范围为1.935% ～12.42%。

Maropoules等的工作相当好的比较了钢中马氏体的屈服强度计算值和实际测定数值。

(未完待续)

Martensitic Transformation(19)

ZHU Zu-chang1，YANG Yi-tao2，WU XU-wei3，WANG Hong3
(1.Shanghai University of Engineering Science，Shanghai 201620，China;2.Shanghai University，Shanghai 200072;3 Shanghai Machine Building Technology Institute Co.，Ltd.，Shanghai 200070，China)

TG111.5

A

673-4971(2014)05-0067-06

2010-08-01

朱祖昌(1941-)，男，教授，主要从事材料表面改性和模具钢的热处理研究。

联系电话:13816379552;E-mail:zhuzuchang@126.com