多元地球化学异常识别的核马氏距离方法

陈永良，路来君，李学斌

1.吉林大学综合信息矿产预测研究所，长春 130026

2.吉林大学地球科学学院，长春 130061

0 引言

在勘查地球化学研究中，分离地球化学背景和异常是十分重要的。在过去的数十年中，研究者们提出了诸多分离单一地球化学指标背景和异常的统计学方法，例如，样本统计直方图法[1]、泛克里格法[2-4]、分形方 法[5-8]、多 重 分 形 方 法[9-11]、奇 异 性 方法[12-13]，等等。由于各种地球化学指标常常以相互影响和相互制约的方式共存于复杂地质系统中，因此，在地球化学异常识别中同时考虑多种地球化学指标的协同效应是十分必要的，充分利用不同地球化学指标之间的关联性有利于减小地球化学异常识别结果的不确定性。在地球化学观测数据满足多元正态分布的条件下，马氏距离是识别多元地球化学异常的较好综合指标[14]。然而，由于地质系统的复杂性、成矿作用的多期多阶段性以及控矿因素的多重性常常导致多元地球化学异常临界面是非线性的和模糊的，用马氏距离定义的平滑超椭球面不能准确表示这种复杂曲面。在这种情况下，用核马氏距离代替马氏距离作为多元地球化学异常识别的综合指标是一种可行的多元地球化学异常识别方法。

核马氏距离是核函数与马氏距离有机结合的产物，用来度量特征空间中样品映像与样品映像总体之间的差异性。核函数的作用是将地球化学样品向量隐式地非线性变换至高维或无穷维特征空间，从而把输入空间非线性可分的多元地球化学异常识别问题转化为特征空间中线性可分的特异值处理问题，同时，强化弱异常并有效抑制数据噪音。核马氏距离识别多元地球化学异常的实质是用特征空间中的超椭球体表示样品映像构成的流型，即多元地球化学背景域[14]，用超椭球面表示特征空间中的多元素背景与异常临界面，用核马氏距离衡量样品映像与样品映像总体之间的差异性。特征空间中的超椭球体对应于输入空间中的复杂几何形体，特征空间中的超椭球面对应于输入空间中复杂地球化学背景与异常临界曲面。因此，特征空间中地球化学样品映像的多元线性异常识别等价于输入空间地球化学异常的多元非线性判别。为数众多的背景样品映像在特征空间中往往构成样品映像流型的主体分布于超椭球体的中心及邻近区域；而数量稀少的异常样品映像常常分布于超椭球体的边缘及外围。因此，可以根据样品映像到映像总体的核马氏距离的相对大小判断样品映像是否为异常样品映像。

把上述多元地球化学异常识别方法应用于吉林省白山市4个1∶20万图幅6607件地球化学样品的多元地球化学异常识别研究。对比分析复合核函数马氏距离、高斯核函数马氏距离、马氏距离和主成分得分的多元地球化学异常识别效果。结果表明，复合核函数核马氏距离是一种有效识别多元地球化学异常的综合指标。

1 核马氏距离计算

从向量x到样本均值为μ、协方差矩阵为C的随机总体X的马氏距离平方定义为

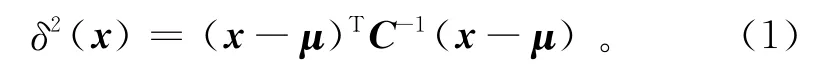
用核函数将向量隐式地非线性变换至特征空间后，向量映像与映像总体之间的差异可用式（1）的马氏距离平方来度量。在特征空间中，由于无法显式地表达向量映像及其样本均值的具体形式，映像总体的协方差矩阵和向量映像到映像总体的马氏距离只能借助核函数来计算；因此，特征空间中的马氏距离称为核马氏距离。核马氏距离计算公式实质上是用核函数表示式（1）的马氏距离。

设输入数据空间Rp中有n个样品数据，xi（i＝1，2，…，n），xi∈Rp用非线性函数Φ（·）把样品从输入空间变换到特征空间F，即

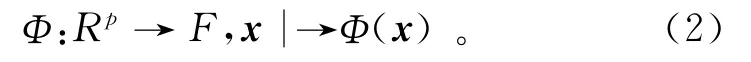
特征空间F为高维欧氏空间或无穷维Hilbert空间。不妨假设特征空间F的维数为m（m≤ ∞），并引入如下m×n阶矩阵：

则特征空间F中n个样品映像的均值向量可以表示为

用核函数表示特征空间F中的向量内积，则n个样品映像两两之间的内积构成的核矩阵可表示为

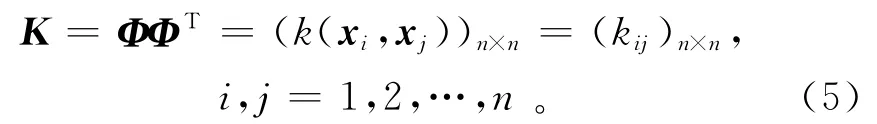
其对应的中心化核矩阵为

特征空间F中任意向量t＝Φ（x）与样品映像集

n个向量Φ（x1），Φ（x2），…，Φ（xn）的内积构成的向量可以写成[16]

相似地，特征空间F中均值向量μΦ与样品映像集n个向量Φ（x1），Φ（x2），…，Φ（xn）的内积构成的向量可以写成[16]

在特征空间F中，任意向量t到样品映像集合的马氏距离可由下式计算[16]：

式中：n为样品数；Ω-1是由中心化核矩阵非零特征值构成的对角阵的逆矩阵；β是由中心化核矩阵非零特征值对应的特征向量构成的矩阵。如果把的较小非零特征值删除，只使用较大特征值及其对应的特征向量来构造Ω-1和β，则可以有效抑制数据噪音对核马氏距离计算结果的影响。

常用的基本核函数模型有如下3种[17]：

①高斯核函数：

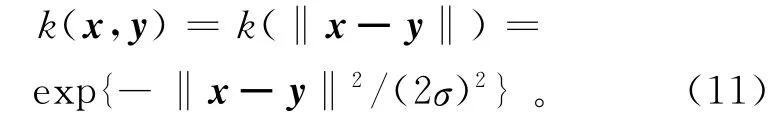
式中：x和y为输入空间中的2个向量；σ为核函数的宽度参数，用来控制核函数的径向作用范围。

②多项式核函数：

式中，a、b、d为自定义的参数，a、b为实数，d 为有理数。

③Sigmoid核函数：

式中，b、c是自定义的参数。

在实际应用中，可以在上述3种基本核函数模型基础上通过加、减和倍乘等运算构造复合核函数模型。

2 多元地球化学异常识别算法

设有n个观测样品，xi＝（xi1，xi2，…，xip）T，i＝1，2，…，n；xi的p个分量分别表示p种地球化学指标的正规化观测值。应用核函数把观测样品向量非线性变换至特征空间，用超椭球体表示n个样品映像在特征空间中的流型，用核马氏距离度量每一个样品映像与样品映像集合的差异性，样品映像的核马氏距离越大，说明样品映像与样品映像集合的差异性越大，相应样品为异常样品的可能性就越大。把每一件地球化学样品对应的核马氏距离计算出来后，可以用阈值法来分离背景样品和异常样品，例如，把样品集合中5%的具有较大马氏距离的样品作为异常样品，则可以据此确定对应的核马氏距离异常下限。

基于核马氏距离的多元地球化学异常识别算法的步骤可概括为以下9步：①构造原始数据矩阵Xp×n＝（x1，…，xn）；②数据正规化；③选择式（11）-（13）的3种基本核函数模型或以3种基本核函数模型为基础构造复合核函数模型，计算核矩阵K；④用式（6）和（7）计算中心化核矩阵；⑤应用Lanczos方法[18-21]计算中心化核矩阵的端部最大特征对；⑥用的数个至数十个端部最大特征对构造矩阵Ω-1和β；⑦对于每一件地球化学样品，用式（8）和（9）分别计算tX和μX；⑧对于每一件地球化学样品，用式（10）计算核马氏距离；⑨按异常样品所占样品总数的百分比确定核马氏距离异常下限，将核马氏距离高于异常下限的地球化学样品标识为异常样品。

3 研究实例

研究区位于吉林省长白山西侧地区，区域大地构造隶属华北板块北缘，地壳演化经历了早期太古宙陆核地体的形成和拼贴过程、古元古代裂谷拉张与闭合过程、中元古代北部边缘地体的挤压拼贴等过程。新元古代-古生代期间，研究区出现局部裂陷，堆积了陆源碎屑岩-碳酸盐岩建造；中生代期间，滨太平洋构造运动产生挤压和拉张应力作用，出现多处断陷盆地，且沿挤压-拉张构造带发生强烈陆相火山喷发及岩浆侵入活动，形成复杂断裂构造格局；新生代以来，太平洋板块的持续作用造成大量基性火山喷发，导致研究区东部被玄武岩覆盖。研究区内断裂构造发育，有超壳断裂、地壳表层断裂、韧性剪切带和脆性断裂。研究区已发现金矿床（点）22处、铜矿床（点）5处、铅锌矿床（点）2处、银矿床1处、铜钴矿1处、锑矿1处和钴矿1处，其中，金英大型金矿床、荒沟山中型金矿床和大横路大型铜钴矿床等是研究区典型工业矿床。研究区不同性质的构造单元成矿系列不同。不同地质历史时期成矿的继承和新生作用存在差异，多种形式的叠加改造-再富集过程导致研究区各成矿带和矿床往往具有多源、多阶段、多期次和多成因等特点[22-24]。研究区不同地质时代地质建造和已知矿床（点）空间分布特征如图1所示。

研究区4个1∶20万图幅共采集6607件化探样品，每件样品用光谱分析方法测试29种地球化学元素含量，用化学分析方法测试6种氧化物含量。Au、Ag元素质量分数单位为10-9，其他元素质量分数单位为10-6，6种氧化物质量分数单位为10-2。研究区化探数据由中国地质调查局数据管理部门负责数据质量评估和图幅接边处理[25]并以Excel表方式提供给用户。根据研究区已知矿种类型及矿床（点）数目，确定Au、Cu、Pb、Zn、Co、Ag、Sb为区域主成矿元素。化探数据经正规化处理后，做29种元素的相关分析。结果表明：主成矿元素中Au、Ag、Pb、Sb与 As、Bi、Hg显著相关，Cu与Bi显著相关，Zn与As、Hg显著相关，故选择主成矿元素Au、Ag、Cu、Pb、Zn、Co、Sb以及与主成矿元素显著相关的元素As、Bi、Hg为区域成矿指示元素。研究区已发现的金矿床（点）数目最多，共占已发现的金属矿床（点）总数的67%，故本文的研究以金矿床为区域找矿的主要目标。根据成矿指示元素类型及相关分析结果，确定4种寻找金矿床的地球化学综合指标：Au-Ag、Au-Ag-As-Hg-Bi、Au-Ag-Cu-Pb-Zn-Co-Sb 和 Au-Ag-Cu-Pb-Zn-Co-Sb-As-Hg-Bi。10种成矿指示元素的频率直方图（图2）可以看出，10种指示元素的频率分布都是正偏态分布，均不服从正态分布。

在核马氏距离应用研究中，核函数及其参数的选择至关重要，不同的核函数模型及参数对应不同的高维特征空间，计算结果不尽相同。目前，核函数的选择还没有一个统一的标准，在实际应用中只能通过经验＋试验的方法确定核函数及其参数。为了对比不同核函数模型的地球化学异常识别效果，用多项式核函数和Sigmoid核函数的加和构造一种复合核函数来计算马氏距离，同时，用高斯核函数模型来计算核马氏距离。这2种核函数模型对应的特征空间分别为高维欧氏空间和无穷维Hilbert空间。实际应用中，多项式核函数的参数a和b通常取1，参数d通常取不小于1的整数，d值越大对应的特征空间越复杂；Sigmoid核函数的参数b和c分别为尺度因子和平移因子，b越大“S”形曲线坡度越陡，c越大“S”形曲线拐点离坐标原点越远；高斯核函数参数σ为曲度因子，σ值越小核函数的非线性性越强。经过试验分析，选择多项式核函数参数a＝b＝1，d＝6；Sigmoid核函数参数b＝4，c＝2；高斯核函数参数σ＝0.5。

用复合核函数和高斯核函数计算出4种组合模式对应的核矩阵后，用核矩阵前10个最大特征值及其对应的特征向量来构造式（10）中的矩阵Ω-1和β。根据tX和μX的定义，核矩阵K的每一列为相应样品与样品集所有样品的内积构成的向量tX；核矩阵K每一行元素算术平均值构成的向量为μX。用式（10）计算每一件地球化学样品的核马氏距离。为了对比核马氏距离与马氏距离及主成分得分的多元地球化学异常识别效果，同时统计计算了4种组合模式的马氏距离和第一主成分得分。

复合核函数计算出的4种组合模式的核马氏距离统计直方图如图3所示；高斯核函数计算出的4种组合模式的核马氏距离统计直方图如图4所示；4种组合模式的马氏距离统计直方图如图5所示；4种组合模式的第一主成分得分统计直方图如图6所示。复合核函数马氏距离频率直方图为单峰型，峰值位于坐标原点右侧附近，为峰值左侧全部缺失而右侧带“长尾”的正偏态分布模型（图3）；这种模型中的绝大多数样品集中分布于坐标原点附近构成背景，少数样品远离坐标原点构成异常，背景-异常分离效果最好。高斯核函数马氏距离频率直方图为近似单峰型，最高峰位于坐标原点右侧附近，为一种最高峰值左侧几乎全部缺失而右侧带“长尾”的近似正偏态分布模型（图4）；这种模型中绝大多数样品松散分布于坐标原点一定距离范围内构成背景，少数样品远离坐标原点构成异常，背景-异常分离效果较好。马氏距离频率直方图为单峰型，峰值位于坐标原点右侧一定距离位置，是一种左侧“截尾”而右侧带“长尾”的正偏态分布模型（图5）；这种模型中大多数样品分布于峰值附近构成背景，少数样品位于远离峰值的“长尾”部构成异常，其背景-异常分离效果不如核马氏距离。第一主成分得分的频率直方图为单峰型，峰值位于坐标原点右侧并远离坐标原点，是一种典型的正偏态分布模型（图6）；这种模型的背景-异常分离效果不如马氏距离。

图1 白山地区简化地质矿产图Fig.1 Simplified map of geologic formations and mineral occurrences of Baishan region

复合核函数计算出的4种组合模式的核马氏距离等值线图如图7所示；高斯核函数计算出的4种组合模式的核马氏距离等值线图如图8所示；4种组合模式的马氏距离异常等值线图如图9所示；4种组合模式的第一主成分得分异常等值线图10所示。

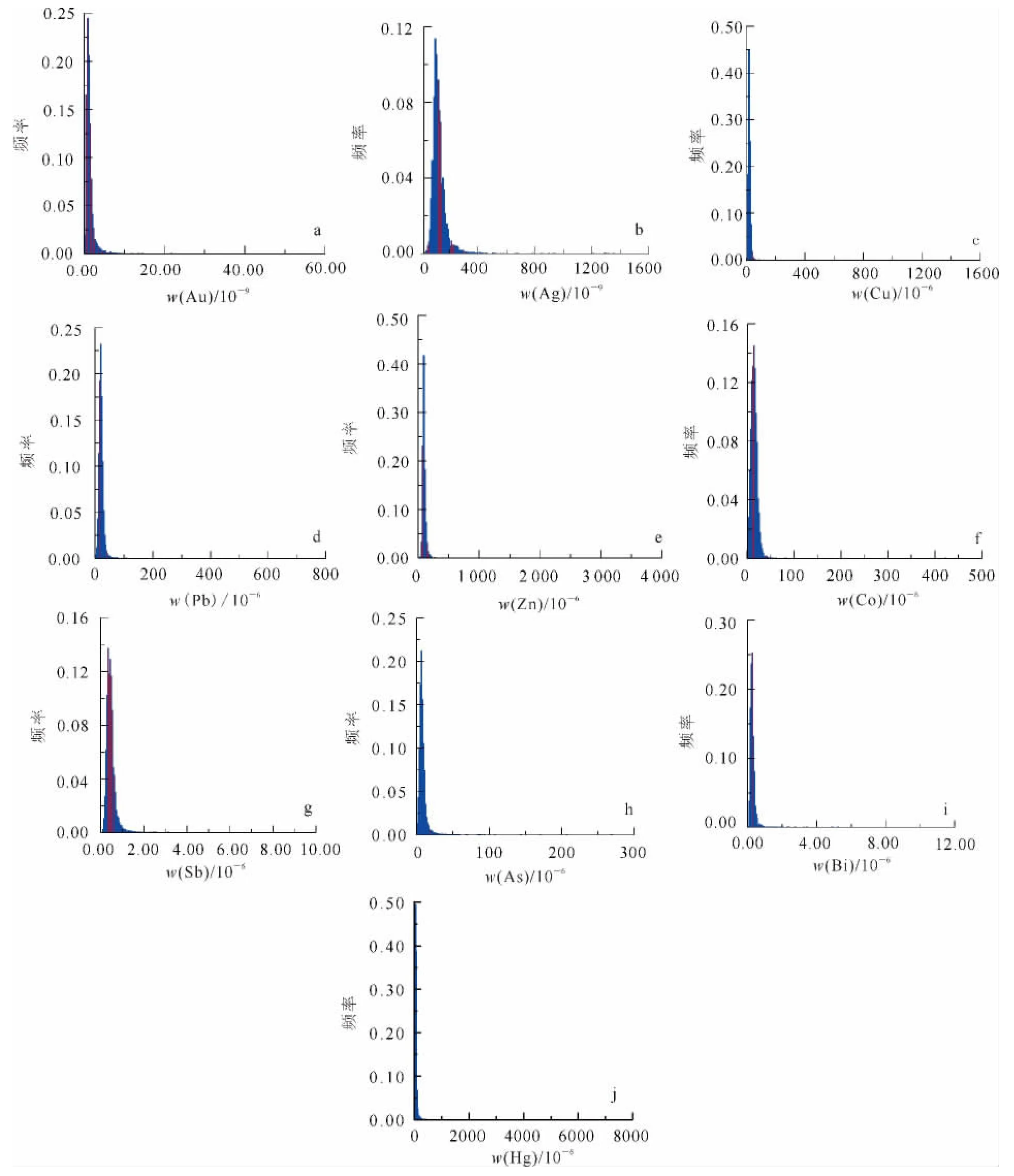
图2 地球化学指示元素统计频率直方图Fig.2 Histograms of geochemical element indicators

从地球化学元素组合异常等值线图（图7-10）可以看出，4种方法综合4种模式（Au-Ag、Au-Ag-As-Bi-Hg、Au-Ag-Cu-Pb-Zn-Co-Sb、Au-Ag-Cu-Pb-Zn-Co-Sb-As-Bi-Hg）的元素组合异常等值线图均在一定程度上反映出研究区存在2个多元地球化学异常集中区（带）：第1个异常集中区位于研究区西南部（南北向22260-22370线和东西向4600-4650线围成的区域），沿北东向展布，区内已发现金矿床18处、铜钴矿床1处、钴矿床1处、铜矿床5处、铅锌矿1处和锑矿床1处；第2个异常集中区位于研究区北部（东西向4710线以北的区域），沿近东西向展布，区内已发现金矿床（点）4处和银矿床1处。

图3 复合核函数对应的核马氏距离统计频率直方图Fig.3 Histograms of kernel Mahalanobis distances with respect to composite kernel function

图4 高斯核函数对应的核马氏距离统计频率直方图Fig.4 Histograms of kernel Mahalanobis distances with respect to Gaussian kernel function

图5 马氏距离统计频率直方图Fig.5 Histograms of Mahalanobis distances

图6 第一主成分得分统计频率直方图Fig.6 Histograms of first principal component scores

图7 复合核函数对应的核马氏距离异常等值线图Fig.7 Contour maps of anomalous kernel Mahalanobis distances with respect to composite kernel function

图8 高斯核函数对应的核马氏距离异常等值线图Fig.8 Contour maps of anomalous kernel Mahalanobis distances with respect to Gaussian kernel function

图9 马氏距离异常等值线图Fig.9 Contour maps of anomalous Mahalanobis distances

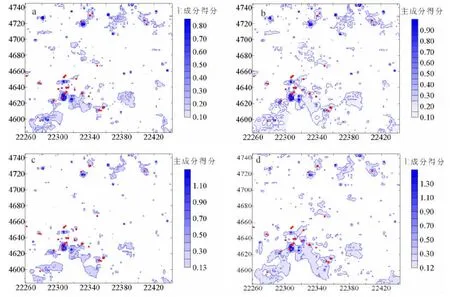
图10 第一主成分得分异常等值线图Fig.10 Contour maps of first anomalous principal component scores

在第1个异常集中区内存在7处明显和3处不明显的异常浓集中心（图7b）。在坐标点 （22310，4630）附近，有3处异常浓集中心共同构成的1处强异常区，该区赋存于3处中生代浅成花岗质侵入岩体构成的弧形岩浆岩带内测（图1），该部位有利于岩浆期后热液的汇集。在该强异常区内，已发现大横路大型铜钴矿床、金英大型金矿床、荒沟山中型金矿床、金矿床（点）1处和铅锌矿床（点）1处等，该强异常区出露的中元古界老岭群是大横路铜钴矿、金英金矿和荒沟山金矿的主要赋矿地层[22-24]。据此推断该强异常区是最有利的多金属成矿远景区。在坐标点（22360，4615）附近存在1处明显和1处不明显的异常浓集中心构成的强异常区，该强异常区内的地质建造组合包括寒武-奥陶纪地层、侏罗纪地层、中生代玄武岩和早元古界片麻状花岗岩，区内已发现4处铜矿床（点），是需要进一步开展工作的多金属成矿远景区。在坐标点（22325，4640）附近存在1处明显的异常浓集中心，位于中生代花岗质侵入岩体与元古界老岭群及早古生代地层三者接触部位，与研究区已发现的锑矿床产出部位相吻合（图1），是1处有利的多金属成矿远景区。在坐标点（22295，4620）附近存在1处明显的异常浓集中心，位于太古界结晶基底和元古界老岭群接触带，与中生代花岗质侵入岩体存在一定距离，与研究区已发现的1处钴矿床产出部位相吻合（图1），是1处有利的多金属成矿远景区。在坐标点（22320，4625）附近存在由2处明显的异常浓集中心构成的强异常区，位于中生代花岗质侵入岩体南侧附近，出露地层包括元古界老岭群、震旦纪和侏罗纪地层，异常区内尚未发现金属矿床，是1处值得进一步工作的多金属成矿远景区。

在第2个异常集中区内，存在大约6处明显和6处不明显的异常浓集中心（图7b）。在坐标点（22330，4720）附近存在1处明显异常浓集中心，位于太古界结晶基底边部，与1处金矿床（点）在空间位置上基本吻合，是需要进一步工作的多金属成矿远景区。在坐标点（22340，4730）附近存在1处无明显浓集中心的异常区，位于太古界结晶基底分布区，异常内已发现金矿床（点）3处，是需要进一步工作的多金属成矿远景区。在坐标点（22410，4725）附近存在1处无明显浓集中心北西向展布的条带状异常，与太古界结晶基底和侏罗纪地层接触带基本吻合，异常内已发现银矿床（点）1处，是需要进一步工作的多金属成矿远景区。此外，尚有5处具有明显异常浓集中心的异常区，分别位于坐标点（22280，4725）、（22320，4735）、（22375，4730）、（22290，4745）及（22420，4735）附近。目前，尚缺少这些异常区的区域地质资料，在这些异常内也没有发现已知金属矿床（点）。

4种多元地球化学异常识别方法的异常识别效果存在微小差别，复合核函数马氏距离的异常识别效果略优于其他方法。以第2种元素组合模式（Au-Ag-As-Bi-Hg）为例：复合核函数马氏距离的多元地球化学异常区面积较小，而且能够反映研究区已知金属矿床（点）的空间分布规律；高斯核函数马氏距离的多元地球化学异常区内的典型异常浓集中心与复合核函数马氏距离基本相似，但是，该方法圈定出一些与已知矿床（点）关系不明、无异常浓集中心的大面积低缓异常区；马氏距离方法圈定的多元地球化学异常，除几处典型异常浓集中心与复合核函数马氏距离相似外，多数异常浓集中心强度不高不够明显，而且该方法也圈定出一些与已知金属矿床（点）关系不明、无浓集中心的规模较大的低缓异常区；主成分方法圈定的多元地球化学异常，有几处典型异常浓集中心与复合核函数马氏距离相似外，其他异常浓集中心与复合核函数马氏距离略有不同，并且该方法圈出了诸多与已知金属矿床（点）关系不明、无浓集中心的规模较大的低缓异常区。上述多元地球化学异常识别结果表明：复合核函数马氏距离方法能够很好地分离多元地球化学背景与异常，其他3种方法的多元地球化学背景与异常的区分效果稍差。

在上述多元地球化学异常识别结果基础上，可以应用对应分析方法统计多元地球化学异常样品与元素的关系，进而对多元地球化学异常进行分类，据此预测各异常区可能发现的金属矿床类型[14]。由于篇幅所限，本文未对此进行研究。

4 结论及讨论

把核马氏距离应用于白山市4个1∶20万图幅多元地球化学数据的异常识别。选择高斯核函数模型和由多项式核函数与Sigmoid核函数构造的复合核函数模型计算核矩阵及核马氏距离，并对比了复合核函数马氏距离、高斯核函数马氏距离、马氏距离和主成分得分4种模型的多元地球化学异常识别效果。结果表明：在正确选择核函数模型及参数的条件下，通过合理取舍核矩阵的端部特征对，核马氏距离计算结果能够有效抑制随机因素干扰，核马氏距离的空间变化规律能够揭示区域多元地球化学成分的空间变化特征，圈定区域多元地球化学异常靶区。

核函数及其参数选择是核马氏距离应用的关键之一。不同的核函数及其参数把地球化学样品非线性映射到不同的高维或无穷维特征空间，相应的核马氏距离计算结果也不尽相同，研究者需要选择能够正确反映研究区已知矿产资源空间分布特征的核马氏距离统计结果。有关核函数模型选择及其参数的确定目前还没有一个统一的标准，在实际应用中，只能靠经验的方式选择核函数并确定其参数。一般情况下，可以选择几种常用核函数模型进行试算，最后通过对比不同模型的应用效果确定使用哪种核函数模型。

（References）：

[1]Rantitsch G.Geochemical Exploration in a Mountainous Area by Statistical Modeling of Polypopulational Data Distributions[J].Journal of Geochemical Exploration，2004，82：79-95.

[2]孟宪伟.单变量因子克立格法实现地球化学场的分解[J].地质与勘探，1993，29（2）：47-50.Meng Xianwei.Single-Variate Factor Kriging for Geochemical Field Separation[J].Geology and Prospecting，1993，29（2）：47-50.

[3]孟宪伟.稳健克立格及其在1∶5万地球化学异常圈定方面的应用[J].物探化探计算技术，1994，16（1）：72-76.Meng Xianwei.Robust Kriging and Its Application in Delineation of Geochemical Anomalies with Scale of 1∶50000[J].Computing Techniques for Geophysical and Geochemical Exploration，1994，16（1）：72-76.

[4]张冬梅，金辉，刘伟.基于Kriging的多重GEP演化建模趋势分析圈定区域化探异常研究 [J].应用基础与工程科学学报，2012，20（3）：526-538.Zhang Dongmei，Jin Hui，Liu Wei.Two Stages GEP Evolutionary Algorithm Based on Kriging for Spatial Trend Surface Analysis and Geochemical Anomalies Evaluation[J].Journal of Basic Science and Engineering，2012，20（3）：526-538.

[5]Cheng Q M，Agterberg F P，Ballantyne S B.The Separation of Geochemical Anomalies from Background by Fractal Methods[J].Journal of Geochemical Exploration，1994，51：109-130.

[6]Cheng Q M.Spatial and Scaling Modeling for Geochemical Anomaly Separation[J].Journal of Geochemical Exploration，1999，65：175-194.

[7]Li C J，Ma T H，Shi J F.Application of a Fractal Method Relating Concentration and Distances for Separation of Geochemical Anomalies from Background[J].Journal of Geochemical Exploration，2003，77：167-175.

[8]Deng J，Wang Q F，Yang L Q，et al.Delineation and Explanation of Geochemical Anomalies Using Fractal Models in the Heqing Area，Yunnan Province，China[J].Journal of Geochemical Exploration，2010，105：95-105.

[9]Bai J，Porwal A，Hart C，et al.Mapping Geochemical Singularity Using Multifractal Analysis：Application to Anomaly Definition on Stream Sediments Data from Funin Sheet，Yunnan，China[J].Journal of Geochemical Exploration，2010，104：1-11.

[10]Afzal P，Khakzad A，Moarefvand P，et al.Geochemical Anomaly Separation by Multifractal Modeling in Kahang（Gor Gor）Porphyry System，Central Iran[J].Journal of Geochemical Exploration，2010，104：34-46.

[11]李晓晖，袁峰，贾蔡，等.基于多维分形模型与指示克里格方法的地球化学异常识别研究[J].地理与地理信息科学，2011，27（6）：23-31.Li Xiaohui，Yuan Feng，Jia Cai，et al.Study on Anomaly Recognition from Geochemical Data Based on Multifractal Model and Indicator Kriging Method[J].Geography and Geo-Information Science，2011，27（6）：23-31.

[12]Zuo R G，Cheng Q M，Agterberg F P，et al.Application of Singularity Mapping Technique to Identify Local Anomalies Using Stream Sediment Geochemical Data，a Case Study from Gangdese，Tibet，Western China[J].Journal of Geochemical Exploration，2009，101：225-235.

[13]Sun X，Gong Q J，Wang Q F，et al.Application of Local Singularity Model to Delineate Geochemical Anomalies in Xiong’ershan Gold and Molybdenum Ore District，Western Henan Province，China[J].Journal of Geochemical Exploration，2010，107：21-29.

[14]纪宏金.地球化学背景与异常划分的多元方法[J].长春地质学院学报，1988，18（3）：311-320.Ji Hongjin.Multivariate Method for Distinguishing Geochemical Background from Geochemical Anomalies[J].Journal of Changchun University of Earth Science，1988，18（3）：311-320.

[15]Scholkopf B，Mika S，Burges C J C，et al.Input Space Versus Feature Space in Kernel-Based Methods[J].IEEE Transactions on Neural Networks，1999，10（5）：1000-1017.

[16]Ruiz A，Lopez-de-Teruel P E.Nonlinear Kernel-Based Statistical Pattern Analysis[J].IEEE Transactions on Neural Networks，2001，12（1）：16-32.

[17]Zhang R，Rudnicky A I.A Large Scale Clustering Scheme for Kernel K-Means[C]／／Proceedings of the 16th International Conference on Pattern Recognition.Washington D C：IEEE Computer Society，2002：289-292.

[18]陈永良，林楠，李学斌.求解大样本核主成分分析模型的Lanczos算法[J].吉林大学学报：地球科学版，2010，40（1）：222-226.Chen Yongliang，Lin Nan，Li Xuebin.Lanczos Algorithm for Kernel Principal Component Analysis on Large Scale Samples[J].Journal of Jilin University：Earth Science Edition，2010，40（1）：222-226.

[19]Wu K S，Simon H.Thick-Restart Lanczos Method for Large Symmetric Eigenvalue Problems[J].SIAM Journal of Matrix Analysis Application，2000，22（2）：602-616.

[20]Stathopoulos A，Saad Y，Wu K.Dynamic Thick Restarting of the Davidson，and the Implicitly Restarted Arnoldi Methods[J].SIAM Journal on Scientific Computing，1998，19（1）：227-245.

[21]Calvetti D，Reichel L，Sorensen D.An Implicitly Restarted Lanczos Method for Large Symmetric Eigenvalue Problems[J].Electronic Transactions on Numerical Analysis，1994，2：1-21.

[22]郭文秀，刘建民.吉林省大横路铜、钴矿床地质特征及控矿因素[J].前寒武纪研究进展，2002，25（3／4）：206-213.Guo Wenxiu，Liu Jianmin.The Geologic Features of Dahenglu Cu，Co Deposit and Ore-Controlling Factors in Jilin Province，China[J].Progress in Precambrian Research，2002，25（3／4）：206-213.

[23]刘文香，满永路，王兴昌.吉林省白山市金英金矿床地质特征及成因探讨[J].地质与资源，2009，18（4）：279-283.Liu Wenxiang，Man Yonglu，Wang Xingchang.Geology and Genesis of the Jinying Gold Deposit in Jilin Province[J].Geology and Resources，2009，18（4）：279-283.

[24]李宝毅，杨振宇，王玉芬.吉南老岭成矿带荒沟山、板庙子金矿床地质特征与成因[J].世界地质，2010，29（3）：392-399.Li Baoyi，Yang Zhenyu，Wang Yufen.Geological Characteristics and Genesis of Huanggoushan and Banmiaozi Gold Deposits in Laoling Metallogenic Belt of Southern Jilin[J].Global Geology，2010，29（3）：392-399.

[25]Daneshfar B，Cameron E.Leveling Geochemical Data Between Map Sheets[J].Journal of Geochemical Exploration，1998，63（3）：189-201.