基于裂步DSR的最小二乘偏移方法

黄建平，薛志广，步长城，李振春，王常波，高国超，曹晓莉，李国磊

1.中国石油大学（华东）地球科学与技术学院，山东 青岛 266580

2.胜利油田物探研究院，山东 东营 257022

0 引言

偏移是利用反射地震数据对地下构造进行成像的重要手段。对炮域偏移方法而言，经典的成像条件认为：正向传播的震源波场与反向传播的接收波场互相关后，可确定反射层的位置[1]。但是事实上，这种成像准则仅仅是正演算子的共轭转置[2]，而不是它的逆。此外，由于采集孔径的限制，速度模型复杂以及波场频宽有限，常规的偏移方法通常对地下结构模糊成像，仅能够提供较准确的构造信息，而对中深部界面反射系数的刻画不够准确，这明显无法满足岩性油气藏勘探开发的要求。

为了解决这些问题，将成像视为最小二乘意义下的反演问题，通过共轭梯度法迭代使误差函数达到最小，得到横向分辨率更高、振幅保真性更好的反演成像结果。最小二乘偏移早期发展由LeBras等[3]和 G.Lambare等[4]完成。Nemeth等[5]提出了基于Kirchhoff的最小二乘偏移方法，并证明了最小二乘偏移（LSM）方法可以减少偏移假频。Duquet等[6]证实了最小二乘偏移在处理起伏地表照明和由不规则粗采样的地震波场引起的成像误差时比Kirchhoff偏移具有更大优势。通过引入数据协方差矩阵，Kuehl等[7]在理论上证明了最小二乘反演的思想可以应用在相移偏移上。Clapp[8]验证了经过几次迭代后，LSM比常规偏移具有更好的成像精度。

国内也有许多学者将最小二乘思想用于偏移、去噪以及数据规则化的研究工作中：贾晓峰等[9]实现波动方程算子的最小二乘偏移；杨其强等[10]进一步发展了基于傅里叶有限差分的最小二乘偏移方法，并通过模型验证了成像效果；沈雄君等[11]详细介绍了基于分步傅里叶变换的最小二乘偏移方法，并给出了Marmousi模型的计算结果；黄建平等[12]推导并实现了基于Kirchhoff成像算子的叠前最小二乘偏移算法。

在前人研究的基础上，笔者推导并实现了基于裂步双均方根（DSR）的最小二乘偏移算法，并将算法用于平层和Marmousi模型进行偏移试算，以测试LSM对复杂地质构造成像的能力，并同常规的裂步DSR偏移算法进行成像效果对比，证实LSM算法的优越性。

1 方法原理

1.1 LSM基本原理

已知线性正演算子L，由地下反射率模型m，可得到合成地震数据d。正演过程可描述为

未加约束条件的最小二乘偏移问题等价于优化特定的目标函数S（m）：

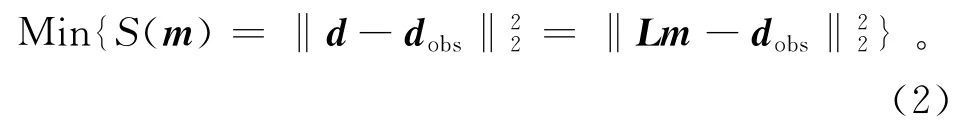
其中：dobs为观测到的记录数据；‖＊‖为L2范数。

能够使目标函数S（m）最小化的最小二乘偏移解可表示为

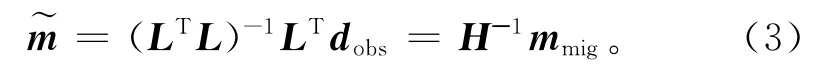
其中：LT为偏移算子（L的共轭转置）；mmig为偏移得到的像，mmig＝LTdobs；H＝LTL为目标函数S（m）的Hessian矩阵。

由（3）式可知求解最小二乘偏移解～m的2种方法：一是直接求解H，二是间接计算，通过共轭梯度法（或最速下降法）不断地优化模型m。Hessian矩阵方法计算速度快，但占用大量内存，且直接求取Hessian矩阵的逆较困难；间接计算方法在每次迭代中均要进行一次正演和偏移计算，计算时间比一般偏移的计算时间多出一个数量级，为正演过程和偏移过程时间和的n倍，其中n为迭代次数，但成像算子计算过程中不额外增加存储空间。笔者采用间接计算方法，用共轭梯度方法来拟合目标函数，通过迭代的次数来控制拟合程度，最终得到符合精度要求的成像结果。

1.2 裂步DSR正传播和反传播算子

将地震记录向下半空间延拓，可求出地下任何一点的波场，进而实现地震波偏移。本文中，假设向下延拓记为反传播，向上延拓记为正传播。其中，正传播算子为反传播算子的共轭算子。为此，在推导二者表示形式的过程中可先推导反传播算子，在得到反传播算子的基础上进行共轭转置求取正传播算子，并用点积标定[13]验证二者的共轭性。

为了满足DSR叠前偏移在横向变速介质中精确成像的要求，Popovici[14]对双均方根方程进行了改进，提出了裂步DSR偏移的算法。从深度z到z＋Δz的延拓过程分为2步：在频率-波数域运用相移项P；在频率-空间域采用时移校正项T。二者可分别表示为

其中：v（z）为参照速度，在层内Δz上是一个常数；ky为中心点波数；kh为偏移距波数；ω为频率。

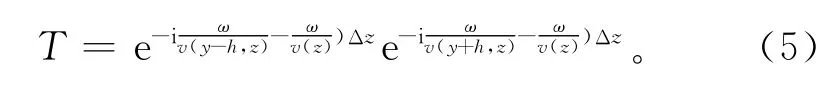
其中：v（y-h，z）为深度z上炮点位置的速度；v（y＋h，z）为深度z上接收点位置的速度。将此两项结合起来，可得到反传播算子表达式：

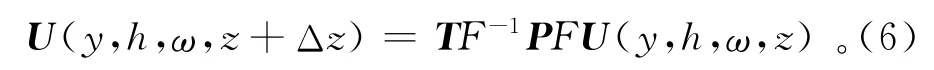
其中：F、F-1分别为中心点、偏移距的二维傅里叶正逆变换，且二者互为共轭；U（y，h，ω，z）为正传播算子。

正传播算子为反传播算子的共轭算子，则正传播算子可表示为

其中：PT、TT分别为P和T的共轭转置，在计算过程中共轭项之间的幂指数符号相反。

为了确保正传播算子和反传播算子互为共轭，需要用点积实验进行检验，算子应满足

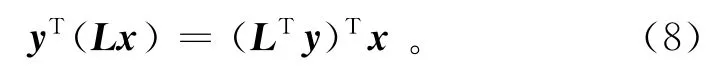
其中：输入向量x，y可取任意值。通过大量模型计算证实：式（6）、（7）所示算子满足式（8）的共轭关系。为此，可根据式（6）、（7）进行裂步DSR的偏移和正演计算过程。最终综合式（6）、（7）与（2），即可实现基于共轭梯度法的裂步DSR最小二乘偏移方法。

2 模型试算

2.1 简单平层模型试算

图1a为该模型速度场，水平采样间隔10m，深度采样间隔10m，最大深度为4km。通过反偏移方法得到平层偏移所需要的叠前炮记录数据。

图1 简单平层模型试算Fig.1 Simple flat layer model trial

图1b为常规裂步DSR偏移的结果，图1c为LSM迭代15次的结果，模型初始值mini＝0，二者的试算结果采用相同的增益显示。对比深度3km处的分界面成像效果可以发现：经共轭梯度法15次迭代的最小二乘偏移得到的同向轴更细，成像分辨率较高，能量收敛性较好，较常规裂步DSR偏移具有更好的保幅性。

图1d给出了15次迭代过程中对应的残差变化关系。可以看到，随着迭代次数的增加，成像结果与真实模型的残差在逐步缩减，这意味着在迭代过程中模型和记录数据匹配的精度越来越高，成像效果越来越好。在迭代次数较小时，残差下降迅速，成像结果收敛较快，成像效果改善明显；当迭代次数较大时，残差变化趋缓，对成像效果的改善效果减弱。

2.2 Marmousi模型试算

在通过简单的平层模型验证了本文方法正确性的基础上，进一步通过国际标准的SEG／EAGE Marmousi模型数据，来检验本文最小二乘偏移方法对复杂模型的适应性。Marmousi模型的速度场如图2a所示，具体参数为：横向497个采样点，纵向750个采样点，速度场水平采样间隔12.5m，深度采样间隔为4m，最大深度3km。基于标准的2D声波有限差分法算法模拟得到单炮记录，并抽取出炮记录对应的共中心点道集如图2b所示。

为了减少计算成本，偏移算法和LSM算法均采用25个频率进行偏移成像，频率为10～60Hz，成像结果如图2c、d。对比图2c和d中圆圈标示的位置可知：裂步DSR偏移算法可以对复杂地质剖面精确成像，而LSM经过5次迭代后的效果要优于常规裂步DSR偏移算法。总的说来，LSM成像剖面的地层信息更丰富，分辨率更高。

图2 Marmousi模型试算Fig.2 Marmousi model trial

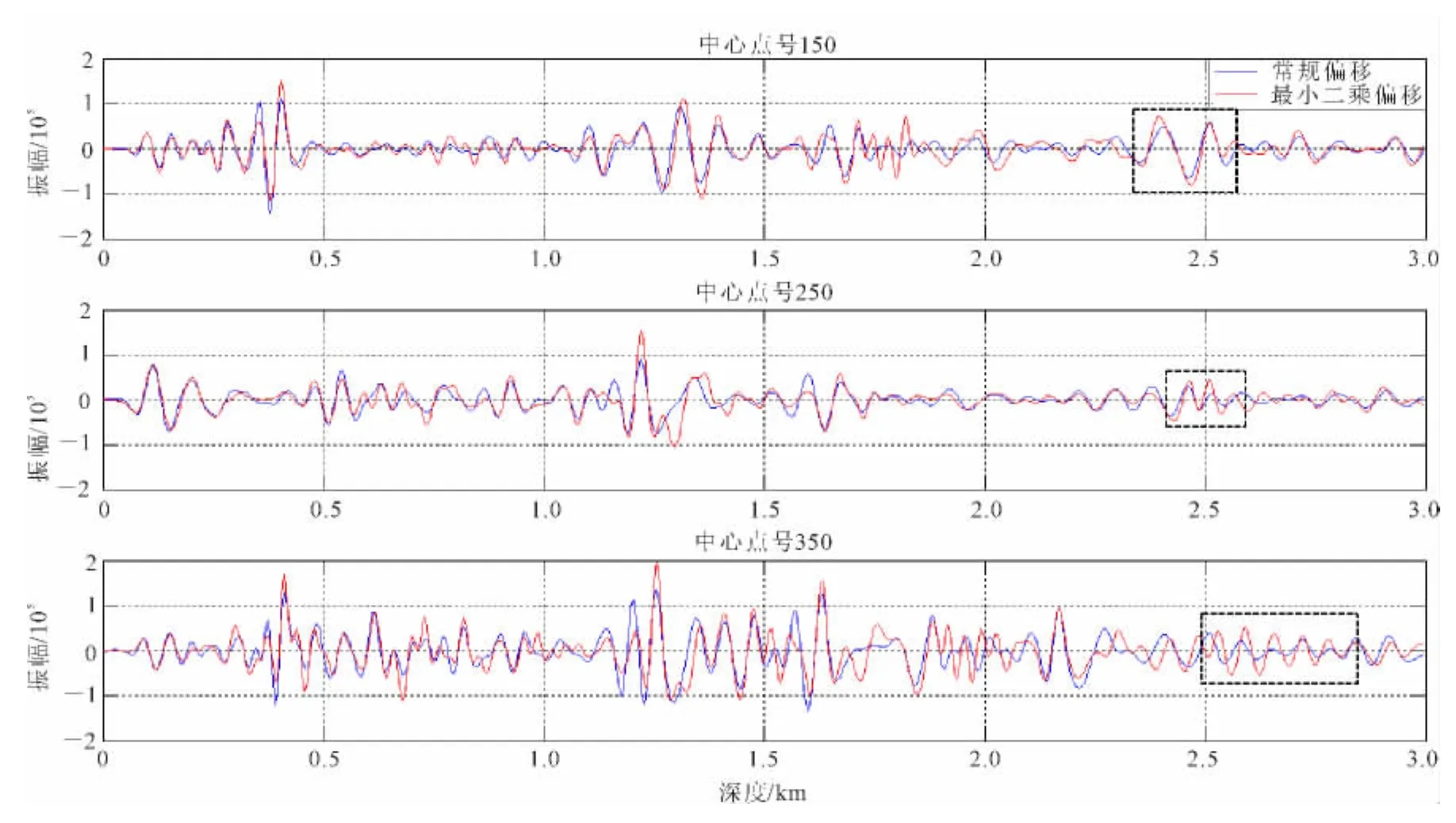
图3 裂步DSR＿LSM和常规偏移相同位置处成像道振幅对比图Fig.3 The comparison of image trace amplitude between split-step DSR＿LSM and common migration

从图2c和d上分别抽取150、250和350网格点位置处的成像道，如图2d中竖线标示位置，提取常规法偏移和裂步DSR＿LSM成像剖面的振幅结果进行对比，成像结果如图3所示。对于浅部构造，裂步DSR偏移和最小二乘偏移得到的振幅幅值和变化趋势基本吻合，首先证明了本文方法的正确性。同时，针对中深层，最小二乘偏移具有较好的保幅性，具体体现在LSM单道偏移结果振幅幅值大于常规裂步法偏移得到的振幅幅值，如图3中虚线框所示。通过成像剖面及单道结果对比可知：LSM可以补偿由于断层和背斜引起的深层能量损失，突显深层局部结构，对中深部构造成像有一定保幅性。裂步法最小二乘偏移之所以能够实现对中深部储层的较好保幅性，可能是因为常规偏移方法偏移算子为正演算子的伴随矩阵而非真正的逆矩阵，随着传播路径的增加，伴随矩阵与逆矩阵的差异较大，所以常规偏移中深部不能很好地实现保幅；而裂步法最小二乘偏移在迭代过程中，不断优化伴随矩阵使之与逆矩阵算子较为接近，从而可从理论上使得中深部储层具有更好的保幅性[15-17]①黄建平，曹晓莉，李振春，等，最小二乘逆时偏移在近地表高精度成像中的应用.石油地球物理勘探，2013，待刊。。

3 结论与讨论

本研究实现了基于双平方根波场延拓算子的最小二乘偏移方法，通过2个理论模型成像试算，验证了LSM经过几次迭代后的成像效果优于常规偏移。LSM成像分辨率优于常规偏移方法主要体现在中深层能量得到了补偿以及中深层构造信息得到了更为准确的刻画。这一优势，对我国西部储层深度在3km以下的碳酸盐岩储层[18-20]具有非常高的实用性。因此，本方法有望在未来西部勘探开发中发挥重要作用。

裂步DSR最小二乘偏移方法相对于Kirchhoff等射线类的最小二乘偏移方法，成像精度更高，不需要计算反射率模型，受地下介质密度误差影响较小。而相对于双程波的最小二乘逆时偏移（LSRTM）方法，成像效率更高，迭代收敛速度更快，同时对于初始速度模型的依赖性更弱，不易陷入局部极小值。再次，裂步DSR最小二乘偏移其反偏移算子也较双程波LSRTM易于求取，但其成像精度低于LSRTM方法。总之，相对于射线类和双程波类的最小二乘偏移方法，裂步DSR兼顾计算效率和成像精度。

当然也应该看到裂步法最小二乘偏移仍然存在一些不足：1）应用LSM对地下构造进行成像时，要考虑残差的变化趋势。在较小迭代次数时，残差变化明显；而迭代次数较大时，残差变化较小，对成像效果的改善能力降低。2）由于每次迭代都要进行一次正演和偏移计算，LSM算法的计算量较大，在应用LSM时，要综合考虑成像精度和计算效率，将二者达到最佳的平衡点。3）在下一步的研究中，也将进一步引入相位编码技术[21-22]，以提高最小二乘偏移的成像效率，同时压制串扰噪音。4）在今后的工作中，逐步将算法用于实际资料的试处理，为复杂构造中深部储层保幅成像研究服务。

（References）：

[1]Claerbout J F.Towards a Unified Theory of Reflector Mapping[J].Geophysics，1971，36：467-481.

[2]Lailly P.The Seismic Inverse Problem as a Sequence of Before Stack Migration[C]／／Conference on Inverse Scattering，Theory and Applications.Philadelphia：Soc Industr Appl Math，1983：206-220.

[3]LeBras R，Clayton R W.An Iterative Inversion of Back-Scattered Acoustic Waves[J].Geophysics，1988，53：501-508.

[4]Lambare G，Virieus J，Madariaga R，et al.Iterative Asymptotic Inversion in the Acoustic Approximation[J].Geophysics，1992，57：1138-1154.

[5]Nemeth T，Wu C，Schuster G T.Least-Squares Migration of Incomplete Reflection Data[J].Geophysics，1999，64：208-221.

[6]Duquet B，Marfurt J K，Dellinger J A.Kirchhoff Modeling，Inversion for Reflectivity，and Subsurface Illumination[J].Geophysics，2000，65：1195-1209.

[7]Kuhl H，Sacchi W D.Least-Squares Wave-Equation Migration for AVP／AVA Inversion[J].Geophysics，2003，68（1）：262-273.

[8]Clapp M L.Imaging Under Salt：Illumination Compensation by Regularized Inversion[D].Stanford：Stanford University，2005.

[9]贾晓峰，胡天跃.滑动最小二乘法求解地震波波动方程[J].地球物理学进展，2005，20（4）：920-924.Jia Xiaofeng，Hu Tianyue.Solving Seismic Wave Equation by Moving Least Squares（MLS）Method[J].Progress in Geophysics，2005，20（4）：920-924.

[10]杨其强，张叔伦.最小二乘傅立叶有限差分偏移[J].地球物理学进展，2008，23（2）：433-437.Yang Qiqiang，Zhang Shulun.Least-Squares Fourier Finite-Difference Migration[J].Progress in Geophysics，2008，23（2）：433-437.

[11]沈雄君，刘能超.裂步法最小二乘偏移[J].地球物理学进展，2012，27（2）：761-770.Shen Xiongjun，Liu Nengchao.Split-Step Least-Squares Migration[J].Progress in Geophysics，2012，27（2）：761-770.

[12]黄建平，李振春，刘玉金，等.碳酸盐岩裂缝型储层最小二乘偏移成像方法研究[J].地球物理学报，2013，56（5）：1716-1725.Huang Jianping，Li Zhenchun，Liu Yujin，et al.A Study of Least-Squares Migration Imaging Method for Fractured-Type Carbonate Reservoir[J].Chinese Journal of Geophysics，2013，56（5）：1716-1725.

[13]Claerbout J F.Earth Soundings Analysis：Processing Versus Inversion[M].Oxford：Blackwell Scientific Publications，2004.

[14]Popovici A M.Prestack Migration by Split-Step DSR[J].Geophysics，1995，59：1412-1416.

[15]Yao G，Jakubowicz H.Least-Squares Reverse Time Migration[C]／／74th EAGE Conference ＆ Exhibition Incorporating SPE.Copenhagen：[s.n.]，2012.

[16]Dai W，Fowler P，Schuster G T.Multi-Source Least-Squares Reverse Time Migration[J].Geophysical Prospecting，2012，60：681-695.

[17]Schuster G T，Wang X，Huang Y，et al.Theory of Multisource Crosstalk Reduction by Phase-Encoded Statics[J].Geophysical Journal International，2011，184：1289-1303.

[18]撒利明，姚逢昌，狄帮让，等.缝洞型储层地震识别理论与方法[M].北京：石油工业出版社，2009.Sa Liming，Yao Fengchang，Di Bangrang，et al.Vuggy Reservoir Seismic Recognition Theory and Methods[M].Beijing：Petroleum Industry Press，2009.

[19]姚姚，唐文榜.深层碳酸盐岩岩溶风化壳洞缝型油气藏可检测性的理论研究[J].石油地球物理勘探，2003，38（6）：623-629.Yao Yao，Tang Wenbang.Carbonate Karst Weathering Crust Deep Hole Seam Reservoirs Can Be Detected Theoretical Study[J].Oil Geophysical Prospecting，2003，38（6）：623-629.

[20]吴俊峰，姚姚，撒利明.碳酸盐岩特殊孔洞型构造地震响应特征分析[J].石油地球物理勘探，2007，42（2）：180-185.Wu Junfeng，Yao Yao，Sa Liming.The Feature Analysis About Seismic Response to Carbonate Special Hole Type Structure[J].Oil Geophysical Prospecting，2007，42（2）：180-185.

[21]Romero L A，Ghiglia D C.Phase Encoding of Shot Records in Prestack Migarion[J].Geophysics，2000，426-436.

[22]Dai W，Wang X.Least-Squares Migration of Multisource Data with a Deblurring Filter[J].Geophysics，2011，76（5）：135-146.