一种新的区域图像插值算法*
2014-09-25余俊荣何彦行
余俊荣, 何彦行, 潘 丰
(江南大学 轻工过程先进控制教育部重点实验室,江苏 无锡 214122)
0 引 言
传统的图像插值算法有最临近插值法、双线性插值法和三次卷积插值法3种,但这3种算法分别存在灰度不连续、轮廓模糊、计算量大等问题。为了提高插值后的图像质量或降低运算时间,国内外学者提出了很多改进的插值方法,主要概括为以下4类:1)基于低分辨图像边缘的插值算法[1~3]:其原理是首先检测低分辨率图像的边缘,然后根据检测的边缘将像素分类处理,对于平坦区域的像素采用传统方法插值,对于边缘区域的像素,设计特殊插值方法。这类算法虽然提高了图像的边缘清晰度,但存在边缘偏离的现象,放大倍数越大,偏离越严重;2) 基于高分辨图像边缘的插值算法[4~6]:此类算法首先采用传统方法插值低分辨率图像,然后检测高分辨率图像的边缘,最后对边缘和附近像素进行特殊处理,以去除模糊,增强图像的边缘。该算法可提高传统方法的边缘对比度,得到较好的主观视觉效果,但由于对图像进行了滤波处理,会导致图像客观质量有一定下降;3)基于边缘保持的自适应插值算法[7~9]:这类算法能有效地去除图像的锯齿效果,但对小面积重复区域处理不足;4)基于区域的插值算法:插值原理是首先将原始低分辨率图像依据不同方法划分成不同区域,然后将插值点映射到低分辨率图像,判断其所属区域,最后根据插值点的邻域像素设计不同的插值公式,计算插值点的值。此类算法无论从主观上还是客观上,图像质量均较好,但文献[10]由于引入了图像分割的方法,算法复杂度加大。
针对已有算法的一些不足,以第四类算法为指导,本文提出了一种新的区域方法用于插值算法中。该算法主要思路为先将待插值图像等分成M×N个方格,分别计算方格4个端点的灰度均方差σ,并将σ与阈值T作比较从而判定方格属于平坦区域还是纹理复杂区域;然后对纹理属性相同的相邻方格进行融合,进而完成整体的区域划分;最后,根据待插值的点在源图像中所属的区域对应地选择最佳插值算法。
1 图像插值区域的划分
1.1 区域概念提出的缘由
传统的插值算法是对整幅图像的像素均进行同样的插值计算,没有考虑图像的局部特性,而图像一般都有相对平坦区域和纹理细节丰富的区域。在平坦区域图像灰度值变化很小,这时采用复杂的插值算法与简单的插值算法相比,插值效果相当,但运算量增加很大;在纹理细节丰富的区域采用复杂的插值算法,则可以得到更高质量的插值效果。因而,在图像的平坦区域采用运算量小的插值算法,在纹理细节复杂的区域采用三次卷积插值,就可以在保持插值后图像质量的同时,减小计算量,降低运算时间[10]。以上便是插值区域这一概念提出的由来。
1.2 新的区域划分方法
本文在综合考虑了相关区域划分方法存在的一些问题后,提出了一种具有广泛适用性的新的区域划分方法。
下面对一幅待插值图像如何进行区域划分作具体说明:
1)首先以它4个端点中的其中1个端点作为X—Y坐标系的原点,然后在X和Y方向上将图像分别进行M和N个等分,如此便得到M×N个方格。
2)很容易得到方格4个端点坐标处对应的灰度值f11,f12,f21,f22及其均值E,计算这4个灰度值的均方差σ,即
σ=
(1)
均方差σ反映了一个方格其4个端点灰度值的离散程度,很明显,σ数值越小,4个端点之间的灰度值跳变就越小,也就表明其灰度纹理相对越平坦。
3)将σ与设定的阈值T作定量比较,如果σ小于T,则将整个方格归为纹理平坦区域(下文均用A表示);否则,归为纹理复杂区域(下文均用B表示),图1为初步划分好的区域示意图。

图1 初步区域划分示意图
4)经步骤(3)划分后的图像,如果存在图1所示的AA(或BB)相邻,则将该区域融合,形成新的区域A(或B),如此作进一步的区域划分,如图2所示。

图2 区域划分最终效果图
为了使示意图像效果对比更明显,这里把属于区域A的用白色填充,属于区域B的则用黑色填充。
完成上述步骤后,对待插值图像的区域划分便实现了。
1.3 关键参数的确定
本文划分方法中有2组关键参数选取尤为重要:
1)M,N的选取:很显然M,N的值越大,图像划分越细,但同时无可避免地也带来了更大的计算量。那么如何选取M,N的值呢?一幅图像是由很多像素组成的,比如:已知一幅图像的分辨率为640像素×480像素,可以得出:这幅图像水平方向有640个像素,垂直方向有480个像素,整幅图像含有640像素×480像素。基于该理论知识,在设计方格大小时,便可以根据实际需要自行设定一个方格水平和垂直方向含有的像素个数,从而得到M,N的值,即
(2)
其中,Lf,Df分别为图像分辨率的水平像素和垂直像素,α为像素的个数,其数值可以自行定义。至此,M,N的取值并没有真正解决,对α取多少合适,业内在初评估一个检测项目能否达到检测精度要求时,通常会采用10像素偏差法来进行评估,即综合考虑硬件误差、软件工具误差和人为误差后,如果系统偏差10个像素或以上时,系统还能达到所需要的检测精度,该检测系统是稳定可行的。举例说明:已知一个检测系统,视野范围为64 mm×48 mm,检测精度要求达到0.4 mm/pixel,如果采用200万像素(分辨率为1 600像素×1 200像素)的工业相机能否达到检测要求?答案是可行的,已知分辨率和视野范围,那么可以很容易得到该检测系统的像素精度P=64 mm/1 600 pixel=0.04 mm/像素(宽边求取结果一样)。
显然,该检测系统即使偏差10个像素,其检测精度仍能达到0.4 mm/pixel。从上述举例可以看出:一旦一个检测系统确定以后,其获取的图像在后期处理时即使有10像素的偏差,也是允许的。基于该准则,本文图像作区域划分时,α的值均取10。
事实上,对图像区域进行划分时,α值的大小不会破坏图像已有的像素精度,本文之所以这样做,只是提供了一种确定M,N值大小的方法,使其在一定程度上更具规范性,并尽量降低后期处理时可能带来的误差。在实际应用中可以根据需要进行一个大小的调整,但α值显然不易过大,否则,会导致步骤(3)中划分的区域没有更多的区分度。
2)阈值T的选取:在图像分割中,也会经常涉及阈值的问题,但其最佳阈值通常都能通过分割算法自行算出,如迭代法和Ostu算法[11]。本文出于计算运行量的考虑,对区域划分时没有引入图像分割的算法,但同时也带来了一个问题,就是对步骤(3)中的阈值T如何选取。本文从公式(1)着手,对其作简化处理如下
t=(f11-E)2+(f12-E)2+(f21-E)2+(f22-E)2.
(3)
定义方格4个端点两两之间的灰度差为Δf,那么,可以得到如下关系式
(4)
将
(5)
代入式(3),并结合式(4),整理得

(Δf2+Δf4-Δf6)2+(Δf3+Δf5+Δf6)2].
(6)
由式(4)可以推出
(7)
代入式(6),得到一个只关于Δf1,Δf2,Δf3的方程,化简整理后即为
(8)
对式(8)作进一步处理,可以得到式(9)
t=
(9)
再结合式(7),有
(10)
一个区域如果纹理相对平坦,其4个端点两两之间的灰度差Δf应该满足如下关系式
-p≤Δfi≤p,i∈[1,2,…,6].
(11)
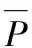
(12)
根据式(11),结合式(12),可以由式(10)推导得到t的如下关系式
(13)
结合式(1),从而得到T的定量公式
(14)
显然n越大,阈值越小,对区域的划分越细,但为了兼顾算法的运算量,建议n取20较为合适,本文对图像进行处理时均采用n=20。
1.4 区域条件下的插值算法
完成区域划分后,就可以进入图像插值的阶段。由于本文采用方格对区域进行划分,所获得区域分属也只是相对而言。因此,如果待插值的点属于区域A,为了保证图像拥有足够的插值精度,那么选用精度高的双线性插值算法而不采用精度较差的最邻近插值算法;如果待插值的点属于区域B或在AB区域的交界线上,那么选用最高精度的三次卷积插值算法。本文完整的算法流程图如图3。

图3 算法流程图
2 仿真结果与分析


图4 Lena仿真结果

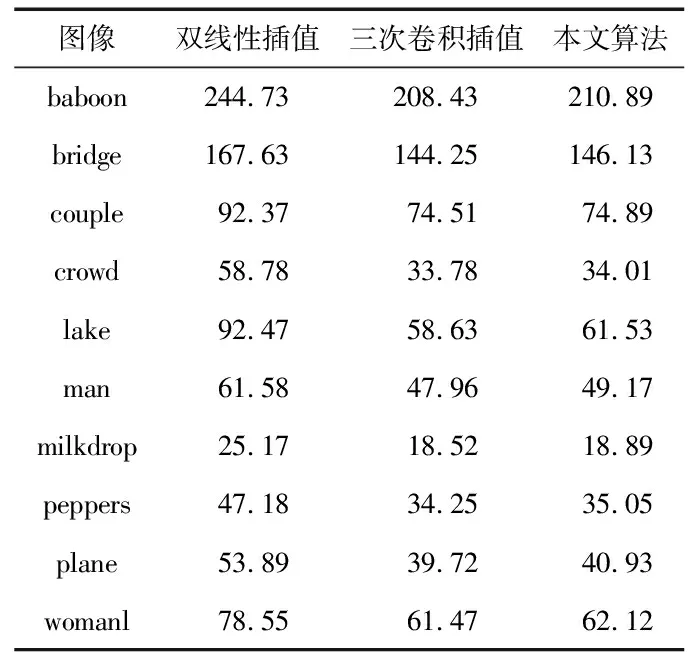
表1 不同算法的均方误差
从表1中可以得出:本文算法插值后获得的图像质量,与三次卷积插值非常接近。算法运算时间方面,由于双线性插值和三次卷积插值均是对整幅图像进行插值,因此,运算时间与图像内容无关,均在200,380 ms左右,而本文的运算时间如表2所示。

表2 算法运算时间
从表2中可以算出:本文算法的平均用时为314 ms,与三次卷积插值相比运算时间降低了17.4 %。
3 结束语
本文提出了一种新的区域划分插值算法,在保持图像质量的同时,一定程度上降低算法运算时间。另外,本文阈值T可以根据不同的图像进行自动调整,具有普遍适用性。仿真实验结果表明:本文算法具有较高的插值精度,图像质量逼近三次卷积插值算法,而运行时间降低了约17.4 %。
参考文献:
[1] 张 雄,毕笃彦,杨宝强.一种保持图像边缘的插值方法[J].空军工程大学学报,2007,8(3):78-80.
[2] Li X,Orchard T.New edge-directed interpolation[J].IEEE Trans on Image Processing,2001,10(10):1521-1527.
[3] 刘政林,肖建平,邹雪城,等.基于边缘的实时图像缩放算法研究[J].中国图像图形学报,2008,13(2):225-229.
[4] 党向盈,吴锡生,赵 勇.基于边缘最大梯度的多方向优化插值算法[J].计算机应用研究,2007,24(9):317-320.
[5] Wang Q,Ward R,Zou J C.Contrast enhancement for enlarged images based on edge sharpening[C]∥Proceeding of IEEE International Conference on Image Processing,Genova: IEEE,2005:762-765.
[6] 高 岚,方康玲,付 旭,等.一种边缘保护的灰度图像插值算法[J].武汉科技大学学报,2004,27(2):188-190.
[7] Mishiba K,Suzuki T,Ikehara M.Edge-adaptive image interpolation using constrained least squares[C]∥Proc of the 17th IEEE International Conference on Image Processing,2010:2837-2840.
[8] Caseiola G,Montefuseo L B,Morigi S.Edge driven image interpolation using adaptive anisotropic radial basis functions[J].Journal of Mathematical Imaging and Vision,2010,36(2):125-139.
[9] Ratner V,Zeevi Y Y.Denoising-enhaneing images on elastic[J].IEEE Trans on Image Processing,2011,20(8):2099-2109.
[10] 符 祥,郭宝龙.区域指导的自适应图像插值算法[J].光电子·激光,2008,19(2):233-236.
[11] 肖 刚,应晓芳,高 飞,等.基于邻域灰度差值的二维Otsu分割方法研究[J].计算机应用研究,2009,26(4):1544-1548.
[12] 陈 超.Matlab应用案例精讲[M].北京:电子工业出版社,2011.
