大规模无线传感器网络环域多扇区多跳分簇路由算法*
2014-09-25,
,
(广东工业大学 自动化学院,广东 广州 510006)
0 引 言
无线传感器网络(WSNs)是由大量传感器节点部署在人们所关心区域,能够在一些苛刻的环境下正常工作[1],在多个领域得到广泛应用。节点能量、计算和存储能力受限,除了最大化传感器节点寿命外,首选均衡整个网络能量消耗,最大限度提高整个网络性能[2]。
根据网络拓扑结构,WSNs中路由可分为两类:层次路由和平面路由[3],层次路由比平面路由能量更高效、扩展性更好。为了避免文献[4]中LEACH随机选取簇头,存在着剩余能量较低节点当选簇头和远距离簇头与基站直接能耗过高问题,文献[5]提出E-LEACH算法,主要考虑了节点能量和数据发送消耗能量优化簇头选举,每轮的时间依赖最优簇规模而变化,簇头由最小生成树发送数据到基站,剩余能量最大的簇头作根节点。文献[6]的EOMC算法通过建立网络能耗优化模型,按最优簇头数分簇,并结合功率控制限制候选簇头选举环带宽度,使产生的簇头分布均衡,分簇时考虑节点剩余能量,以均衡节点能耗,达到延长网络寿命的目的。其最优分簇个数,各环内构建规模不同的簇以克服网络中的“热点”问题,但是每轮都进行簇头选举存在开销过大,而文献[8]提出一种基于最优簇头个数的分环多跳算法。通过分析一个簇内簇头对簇内节点能量消耗的影响,根据发送和中继数据包数量计算传感器网络能量消耗,通过计算能量消耗,得到其网络内最优簇头个数,但是以固定频率随机选取簇头并不能保证簇头分布的均衡性。为避免文献[7]中RBMC每轮都进行簇头选举能耗过高问题,文献[8]提出的ERBMC采用多轮机制簇头选举且簇头选举时考虑节点剩余能量。文献[8,9]分析簇头对簇内节点能耗的影响,确定发送和中继数据包数量并计算网络能耗,最后得到网络内最优簇头个数,但是以固定频率随机选取簇头并不能保证簇的均衡分布。文献[10]提出CEBCRA,簇头选举考虑剩余能量和节点分布密度;节点根据簇头消耗代价选择入簇;簇头根据自己到基站经不同路径时的能耗代价,选取能耗最优的中继簇头,降低通信能量消耗。
上文提到的算法对簇头选举进行改进,簇头选举考虑节点分布,剩余能量;计算得到网络内能量消耗最低时最优簇头数,取得了一定效果。但实际中节点常常随机分布,统一分簇并不能有效解决簇头分布不合理造成能耗不均衡的问题。因此,本文提出一种环域多扇区多跳分簇路由(MMCR)算法。
1 系统模型
1.1 能耗模型
本文采用和文献[9]相同的能耗模型。节点发送k位数据到距离为d的地方,能量消耗公式如下
(1)
接收k位数据能量消耗为
ERX=k×Eele,
(2)
(3)
式中k为传输数据包含两进制数的位数,d为节点发送距离。当节点发送距离小于阈值d0时,采用自由空间模式,功率放大损系数为εfs;否则,采用多路径衰减模式,功率放大系数为εamp。
由式(1)、式(2)看出数据发送比接收消耗能量更多,能量消耗与距离的指数关系呈正比,因此,应避免过远距离的传输造成能量消耗代价过高。
1.2 网络模型
N个同构节点随机分布半径为R基站为中心的圆形区域,如图1。
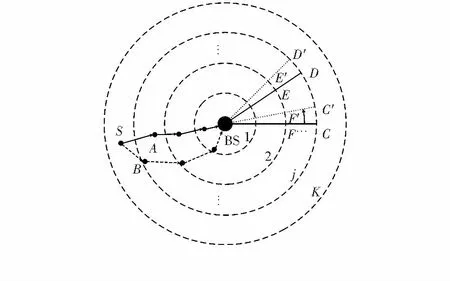
图1 网络模型
网络划分为基站为中心分为等间距D的K个同心圆,其中,R=D×K,由基站向外依次为1,2,…,j(j (4) 具体计算过程见文献[7],进而推到得到任意环消耗能量最少时最优分簇个数 (5) MMCR算法根据分环后各环能量消耗最低时候的最优分簇个数,各环根据最优分簇个数对环域进行多扇区划分、采用多轮旋转机制选择簇头,簇头选举考虑剩余能量、与基站距离因素。 MMCR算法分为3个阶段:环域多扇区划分、簇头选举、稳定阶段。 由于LEACH,E-LEACH算法通过随机选举簇头,存在着网络区域内簇头数目和簇头位置不确定的问题,尤其当网络规模较大的时候,LEACH,E-LEACH簇头个数、位置随机地让有的区域簇头分布过于密集,而有的区域簇头过于稀疏,导致网络消耗能量不均衡。 针对LEACH,E-LEACH出现的不足,尤其网络规模较大时更为突出。RBMC,ERBMC算法对网络进行分环,在更小的环域内通过计算得到其能耗代价最低时每环分簇个数,确定了各环内分簇个数,即保证了整个网络内的分簇数量,同时簇头选举限制于每个环域内,在规模较大的网络中使簇头分布更加均衡。 通过上面几种算法特点分析,由上节对各环能量消耗最低时得到最优分簇个数,对于任意第j环最优簇分簇个数为Mj,可根据公式(5)计算得到。对于任意第j环最优分簇个数为Mj,第j环被分为以基站为中心的Mj个圆心角度都为θ=2π/Mj的扇区,各环的扇区划分相互独立,互不影响。这样,根据分环多跳模型每环消耗能量最低时得到的最优分簇个数,把分环后网络区域里面每个环域里面进行扇区划分,每个扇区作为一个簇。通过这样的办法不仅保证的簇分布的均衡性,而且簇头只在环域的扇区内内选举,确保了簇头分布的均衡,进而使整个网络消耗能量均衡。 由于簇的规模不同,簇头距离基站距离,需要收集转发簇内成员信息量不同,同时还对其他簇头转发来的数据融合处理并转发,导致每轮结束后个簇头能量消耗出现较大差异。合理地选举簇头可以更好地均衡网络内节点能量消耗,降低网络通信能量消耗,延长网络生命周期。 簇头选举综合节点剩余能量、基站距离2个参数。根据权重最高的节点当选簇头,即剩余能量大、距离基站近的节点当选簇头概率大,若不止一个节点满足,则选举ID较小者,权重公式如下 (6) 式中Eres,Eini,dBS(i),R分别为当前节点剩余能量、节点初始能量、节点距基站距离、网络区域半径;影响因子α与节点性质相关的常数。 每个环域的各个扇区(簇)内簇头选择完成后,簇头发出广播信息CH_MSG_AD告知扇区内成员节点自己成为簇头,所有的扇区内成员节点接收到该信息后,自动默认扇区划分为它们所在的簇。接下来的过程中按照时分多址(time division multiple access,TDMA)各自所分配时隙,将自己感知信息和能量信息发送簇头,其它未轮到的成员节点保持工作在睡眠状态,降低节点能量消耗。由于计算消耗能量远远小于通信能量消耗,簇头只把节点感知信息发送至基站并不发送节点能量信息,簇头计算其簇内所有节点的平均能量,根据其平均能量和当前簇头剩余能量关系,为下一轮簇头选举做准备。 任意环中任意扇区内,如果簇头能量低于其划分扇区的簇内平均能量,则进行新一轮簇头选举。各环区域划分扇区相互独立,即分簇相互独立,任意环簇头选举也互不影响。如图1所示,对于任意第j环中以基站为中心的圆心角为θ=2π/Mj的扇区CDEF这时第j环候以一个角度θ/n进行逆时针绕基站旋转到C′D′E′F′,通过n次旋转第j环完成一个周期回到初始位置,这样就实现了多选旋转机制的簇头选举。通过计算各个扇区内平均能量,如果扇区内簇头能量高于平均能量,则继续担任簇头,降低了每次都要选举簇头能量开销。只有当簇头能量低于其扇区内能量时才通过逆时针旋转改变环域扇区的划分,对其所在环内进行新一轮的簇头选举,避免了整个网络大规模簇头选举节点能量消耗过高的问题。 簇头选举完成,由于对每个环域内多扇区分簇,簇规模较小,簇内成员节点采用单跳方式与簇头通信更加高效,但是对于规模较大网络,距离较远簇头无法直接与基站通信或者通信代价过高,除第一环外,其它环显然采用多跳更为合理。为避免传统多跳选取距离自己向基站方向最近的簇头作为中继节点可能发生“缠绕”问题,如图1中节点S—B—BS路径。j环簇头结点集合为Nk{k|k=1,2,…,Mj},第(j+1)环簇头可根据下式选择j环中继簇头 d=d2(k,Nk)+d2(Nk,BS), (7) 式中d2(k,Nk),d2(Nk,BS)分别为(j+1)环节点到j环簇头Nk距离和Nk到基站距离。(j+1)环簇头选择距离权值d最小的j环簇头为下一跳中继节点,并且限制多跳次数小于j。 仿真实验中将8 000个节点随机分布在半径720 m区域,K=9,D=80 m。本文将MMCR与LEACH,E-LEACH,ERBMC在Matlab 2010进行仿真,仿真参数:初始节点能量为1 J;数据融合能耗为50 pJ/bit;数据包大小为500 bit;Eele为50 nJ/bit;εfs为10 pJ/bit/m4;εamp为0.001 3 pJ/bit/m2;α为0.7;n为4。 对于MMCR和LEACH,E-LEAC,ERBMC剩余能量总量、存活节点数随轮数变化的情况分别如图2和图3所示。 图2 剩余能量总量与轮数关系 从图2明显看出:在轮数相同时,MMCR的剩余能量总量要高于LEACH,ERBMC,E-LEACH,其中能量消耗为初始总能量50%时,LEACH,ERBMC,E-LEACH,MMCR运行轮数分别为357,673,467,802轮,可见MMCR对于整个网络能量利用率更高。因为通信能量消耗占网络内能量消耗比例较大,通信中发送信息能量消耗是主要部分,发送能量消耗主要依赖于发送距离,这里采用均衡分簇和多轮旋转机制簇头选举均衡了簇的分布,降低了各网络内节点的通信能耗,在各环域内划分根据最优簇头数划分了多扇区,从扇区内、环内均衡能耗从而均衡整个网络的能耗均衡,提高了网络能量利用率。 图3 存活节点数目与轮数关系 图3可以看到:首个节点死亡时,LEACH,E-LEACH,ERBMC运行轮数分别为387,510,671轮,而MMCR运行轮数为814轮;节点死亡50%时候,LEACH,ERBMC,E-LEACH,MMCR运行轮数分别为628,928,841,1153;节点剩余能量总量耗尽时或节点全部死亡时,LEACH,ERBMC,E-LEACH,MMCR分别为1028,1400,1202,1583。明显看到经历同样轮数时,MMCR存活节点数、稳定性均优于LEACH,ERBMC,E-LEACH,尤其网络规模较大时候,MMCR优势更为明显。 图4所示为4种算法的基站接收数据总量与轮数之间关系,明显看出:MMCR在向基站数据发送时比LEACH,E-LEACH,EMBCR更为高效,由于对网络进行多扇区分簇、保证了簇的均衡形成、簇的规模更优化、簇头的分布更加均衡,从而提高了网络内基站接收数据总量。 图4 基站接收数据量与轮数关系 本文对LEACH,E-LEACH,ERBMC等路由算法进行分析研究,然后提出MMCR算法:对网络进行分环,依据各环能量消耗最低时得到最优簇头数Mj,对各环进行扇区划分,即分簇;每扇区内根据能量和距离产生簇头,由簇头计算扇区平均能量按照多轮旋转机制选举;簇内单跳,簇间根据距离权值选择下一跳中继簇头,单跳、多跳相结合与基站通信,均衡了节点能耗,降低网络内通信能耗,延长了网络寿命。实验证明:MMCR算法均衡了网络能耗,在能量利用率、网络寿命方面要优于LEACH,E-LEACH,ERBMC,同时数据发送效率也获得较好效果。 参考文献: [1] Patel H,Pandya N.Study and review of routing protocols for wire- less sensor networks[J].International Journal of Engineering,2013,2(1):1-7. [2] Singh S K,Singh M P,Singh D K.A survey of energy-efficient hierarchical cluster-based routing in wireless sensor network-s[J].International Journal of Advanced Networking and Application (IJANA),2010,2(2):570-580. [3] Manap Z,Ali B M,Ng C K,et al.A review on hierarchical routing protocols for wireless sensor networks[J].wireless Personal Communications,2013(2):1-28. [4] Heinzelman W R,Chandrakasan A,Balakrishnan H.Energy-efficient communication protocol for wireless microsensor network-s[C]∥Proceedings of the 33rd IEEE Annual Hawaii International Conference on System Sciences, 2000:10. [5] Xu J,Jin N,Lou X,et al.Improvement of LEACH protocol for WSN[C]∥2012 The 9th IEEE International Conference on Fuzzy Systems and Knowledge Discovery (FSKD),2012:2174-2177. [6] 易 军,石为人,许 磊.基于能量优化模型的无线传感器网络分簇算法[J].高技术通讯,2010 (2):157-162. [7] 刘 志,裘正定.基于分环多跳的无线传感网分簇路由算法[J].通信学报,2008,29(3):104-113. [8] Ren Z,Chen Y,Yao Y,et al.Energy-efficient ring-based multi-hop clustering routing for WSNs[C]∥2012 IEEE Fifth International Symposium on Computational Intelligence and Design (ISCID),2012:14-17. [9] Nam C S,Han Y S,Shin D R.Multi-hop routing-based optimization of the number of cluster-heads in wireless sensor network-s[J].Sensors,2011,11(3):2875-2884. [10] Kuila P,Jana P K.An energy balanced distributed clustering and routing algorithm for wireless sensor networks[C]∥2012 IEEE 2nd International Conference on Parallel Distributed and Grid Computing (PDGC),2012:220-225.2 MMCR算法
2.1 环域扇区划分
2.2 多轮旋转机制选举簇头
2.3 稳定阶段
3 仿真分析
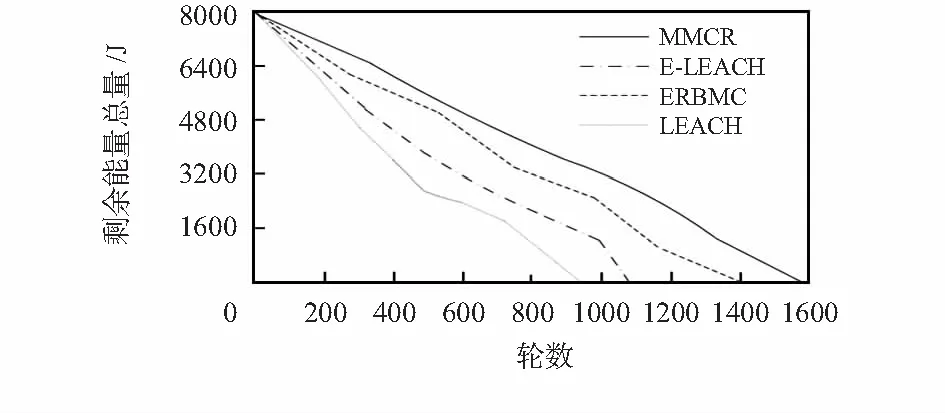
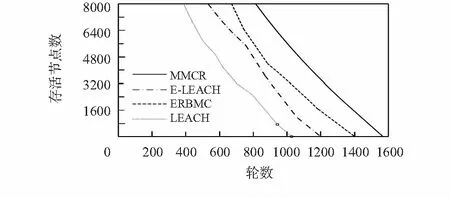

4 结 论
