基于各向异性岩石物理的缝隙流体因子AVAZ反演

陈怀震，印兴耀，高成国，张广智，陈娇娇

1中国石油大学（华东）地球科学与技术学院，青岛 266555

2新疆油田勘探开发研究院，新疆 克拉玛依 834000

1 引言

裂缝储层的预测和缝隙流体的识别成为当前研究的重点（张春贺等，2011；孔丽云等，2012；彭真明等，2008）.而裂缝岩石物理模型可以将储层缝隙特征、流体充填类型与地震响应较好地联系起来，为储层反演和流体识别奠定了基础.随着宽方位地震采集和处理技术的发展，对地震数据的振幅解释也越来越深入（李凡异等，2012；曲寿利等，2012；尹志恒等，2012）.大量研究表明，裂缝储层表现出较强的各向异性，其地震反射系数随入射角和方位角的变化（AVAZ）特征明显，因此基于AVAZ特征分析的裂缝储层反演和缝隙流体预测工作也越来越受关注.

针对裂缝岩石物理模型建立和缝隙流体识别工作，国内外地球物理学家们做了大量探索.Xu等（1999）对碳酸盐岩孔隙类型进行了研究，并且提出碳酸盐岩岩石物理模型的构建流程.Kumar和Han（2005）致力于碳酸盐岩孔隙度和孔隙纵横比的定量分析，实现了碳酸盐岩孔隙的合理划分.Xu和Payne（2009）讨论了碳酸盐岩的弹性性质，对比了碎屑岩和碳酸盐岩的纵横波速度特征，并对碳酸盐岩横波速度进行了预测.Hudson（1980）提出了薄硬币形状的微小裂隙的岩石物理理论，Schoenberg（1980）构建了大尺度裂缝线性滑动模型.Bakulin等（2000）将Hudson模型和Shoenberg模型结合起来，分析缝隙充填物对各向异性参数的影响.

Mallick等（1998）最先利用地震方位角道集数据进行弹性参数反演；Bachrach等（2009）对裂缝储层进行了重构，提出AVAZ反演估测裂缝储层参数的方法；Downton等（2010）基于Schoenberg线性滑动模型进行了岩石物理参数的反演.张广智等（2012）研究了各向异性AVO特征，并对裂缝弹性参数叠前反演方法进行了试算.Neut等（2007）分析缝隙流体对储层各向异性AVO梯度的影响，初步提出缝隙流体因子反演方法.Shaw和Sen（2006）利用AVOA地震数据估算垂直裂缝介质的流体因子.Chen等（2012）依照岩石物理分析，结合各向同性流体识别方法，对各向异性储层流体识别进行了初探.

本文结合线性滑动模型，选择有效的缝隙流体指示因子，并研究流体因子与缝隙孔隙度、缝隙纵横比、缝隙流体类型和饱和度之间关系.完成了基于裂缝岩石物理模型的储层反射系数近似公式和缝隙流体因子的AVAZ反演方法的理论推导，并利用工区实际测井数据和复杂裂缝模型对AVAZ缝隙流体因子反演方法进行试算，取得了较好效果.

2 基本原理

2.1 裂缝介质刚度矩阵

基于弱各向异性理论，具有水平对称轴的高角度裂缝介质弹性系数矩阵C可以描述为各向同性背景系数矩阵Ciso与各向异性扰动Cani之和：

其中，C、Ciso以及Cani分别为

λ和μ是不含裂隙岩石的拉梅参数，ΔN和ΔT是Schoenberg线性滑动理论中的裂缝正向差值和切向差值，数值变化为0～1.

Hsu和Schoenberg（1993）研究了裂缝正向差值ΔN和切向差值ΔT与裂缝柔度系数KN和KT之间的关系：

从上式可知，ΔN和ΔT独立地与裂缝柔度系数有关，不存在相关性.

2.2 缝隙流体指示因子

Schoenberg和Sayers（1995）提出KN／KT可以用来指示缝隙流体.根据方程（2）可得

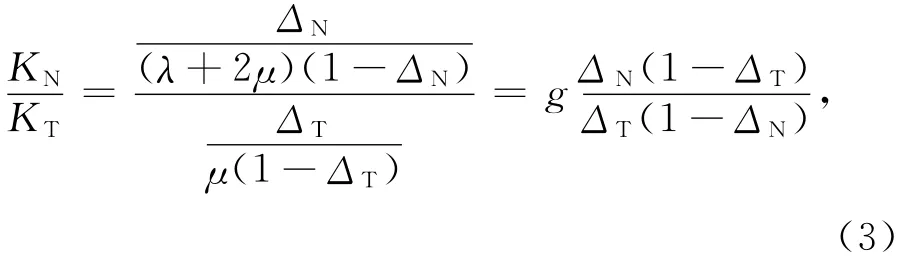
正差值和切差值与缝隙参数（裂缝纵横比，裂缝密度）以及充填物的相互关系如下：

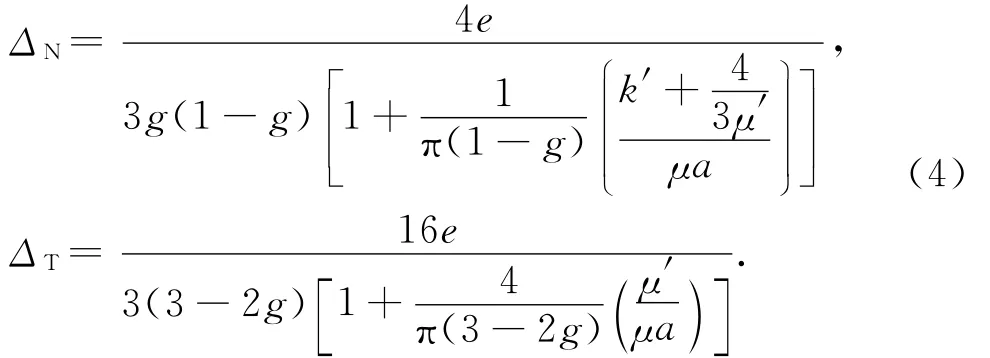
式中，k′和μ′是缝隙中充填物的体积模量和剪切模量，a是裂隙纵横比，e为裂缝密度.建立裂缝储层模型，分别讨论缝隙流体指示因子KN／KT与裂缝纵横比a、裂缝密度以及缝隙充填物之间的关系，缝隙充填流体（油、气、水）的弹性参数（体积模量K、剪切模量μ）以及背景介质的弹性参数（纵波速度α、横波速度β、密度ρ）如表1所示.

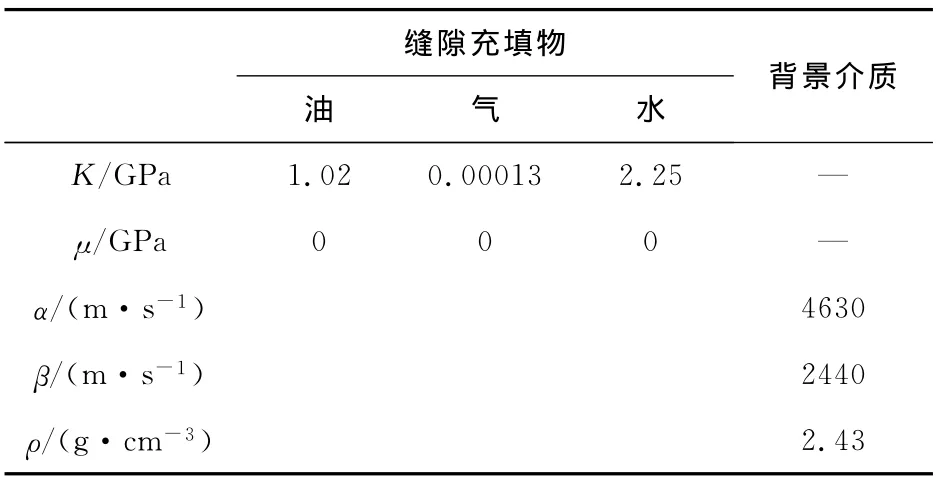
表1 缝隙充填流体与背景介质的相关参数Tabel 1 Parameters of fracture filled fluid and background media

图1为不同裂缝纵横比a，不同裂缝密度e和不同流体充填时KN／KT的变化.图1a为不同流体充填时，流体指示因子KN／KT与裂隙纵横比a之间的相互关系，图中可以发现当缝隙含气时流体指示因子随裂缝纵横比的变化较为明显.图1b为当缝隙充填油水时，不同含水饱和度和不同裂缝密度下流体因子值，可以看出油水混合时流体因子值较小，趋近于0；图1c和1d代表水气混合和油气混合、不同流体饱和度和不同裂缝密度时流体因子值变化特征，可以看出两种情况下的流体因子值均较大，而且缝隙含气时流体因子的变化特征基本相同.图1验证了KN／KT可以作为缝隙中充填流体类型的指示参数.因此，推导出包含流体信息的裂缝储层反射系数近似公式，在已知叠前地震数据信息的前提下，结合测井信息，即可实现裂缝储层流体因子的AVAZ反演.

2.3 基于流体因子参数的裂缝介质反射系数

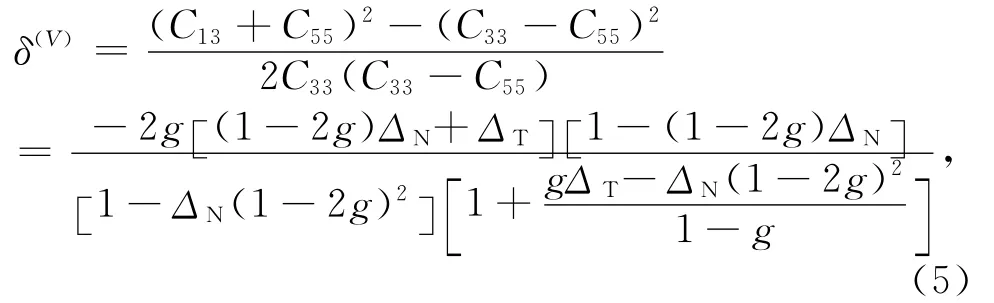
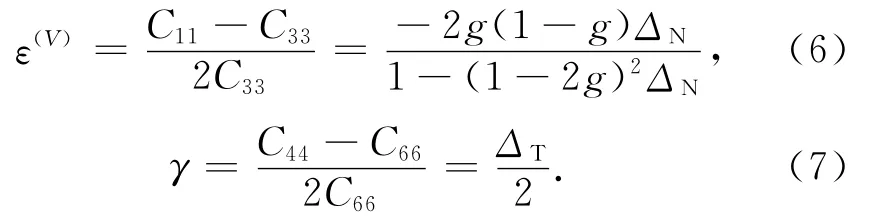
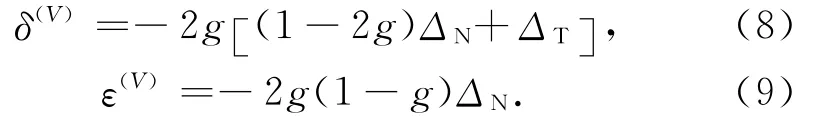
Ruger（1996）详细研究了HTI介质反射特征，并推导了HTI介质的反射系数近似公式：

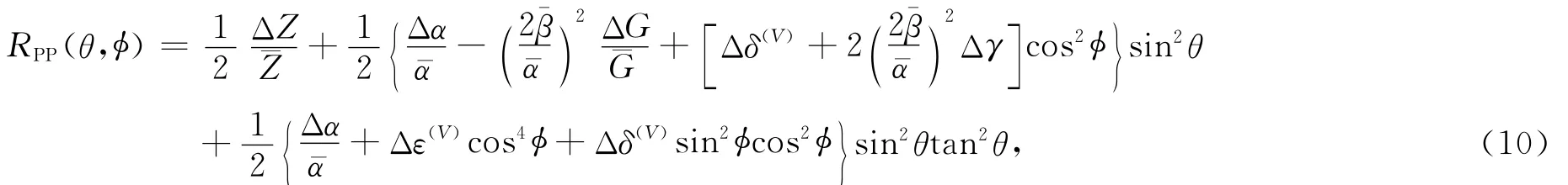
将方程（7）、（8）和（9）带入方程（10），同时基于弱各向异性近似理论，将HTI介质反射系数RPP（θ，φ）可表示为各向同性背景反射系数和各向异性部分扰动相加的近似形式：

假定现有不同方位角φ1和φ2的叠前角度道集，当入射角θ小于30°时，可舍掉sin2θtan2θ，两者反射系数差值为

上式描述了裂缝正向差值ΔN和切向差值ΔT与裂缝介质反射系数RPP（θ，φ）之间的关系，将地震记录和裂缝岩石物理有效地联合起来.通过地震记录AVAZ反演求解裂缝正向差值ΔN和切向差值ΔT，利用方程（3）可求得缝隙流体因子值.

2.4 含流体裂缝储层地震响应特征

表2 含不同流体裂缝介质模型（Shaw and Sen，2006）Table 2 Fractured medium with fluid of different types（Shaw and Sen，2006）

从图2可以看出，当缝隙含气，部分充填油水和完全充填油水时，其反射系数随入射角和方位角的变化特征具有较大差别.因此通过分析储层的AVAZ特征，进而实现储层缝隙流体的AVAZ反演.

2.5 流体因子AVAZ反演

本文通过求解不同方位的地震反射系数，从而实现正向差值ΔN和切向差值ΔT的反演，进而求取流体指示因子.

不同入射角时，方程（12）可以改写为矩阵形式：

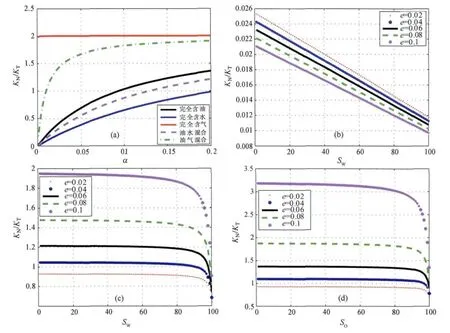
图1 流体指示因子KN／KT与裂缝纵横比α、裂缝密度及缝隙流体之间的关系（SW、SO分别为含水饱和度和含油饱和度）Fig.1 Fluid factor variation with fracture aspect ratio，fracture density and filled fluid type

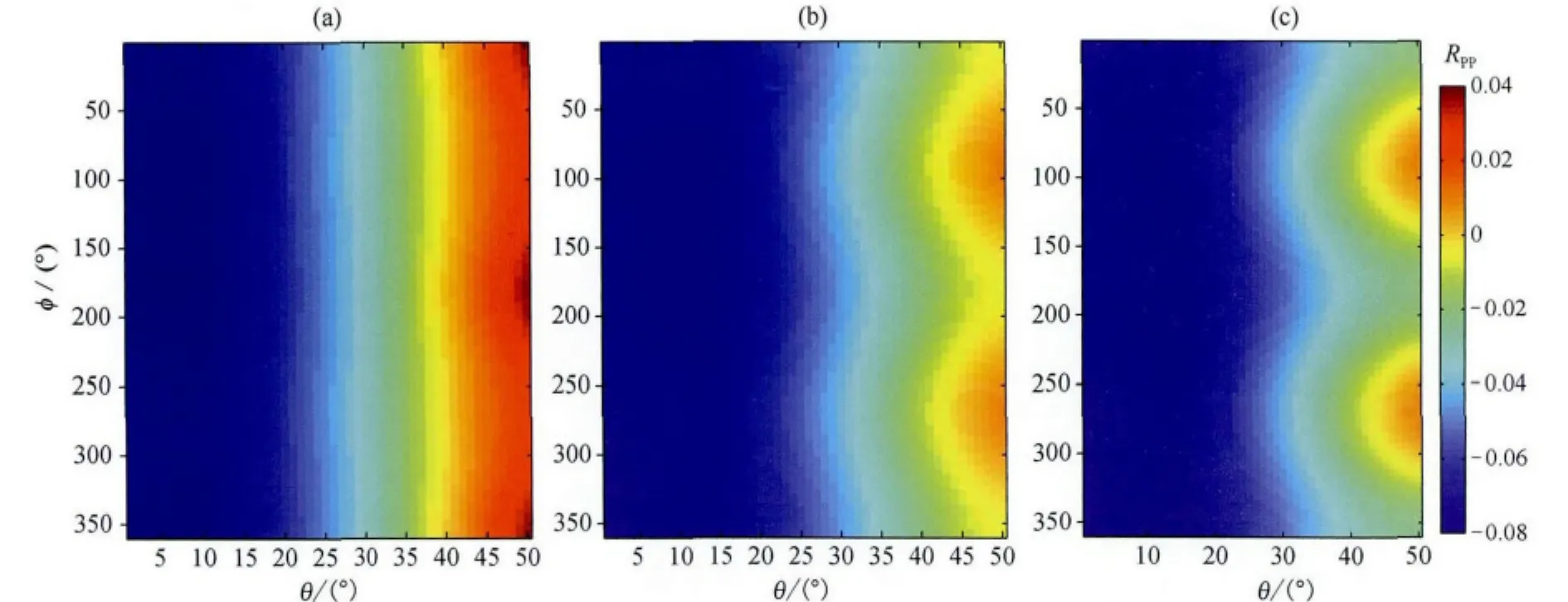
图2 不同流体充填裂缝介质的反射系数特征（a）缝隙含气；（b）缝隙部分含油水；（c）完全充填.Fig.2 Reflection coefficient variation with incidence and azimuth angle（a）Gas filled；（b）Partially filled；（c）Fluid filled.

假定，

当添加随机噪声N时，未知数X可以利用反复迭代最小二乘方法进行求解：

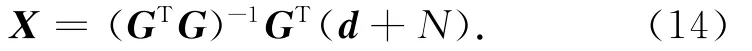
3 数据试算

3.1 缝隙流体因子计算和分析

选取某碳酸盐岩裂缝发育工区A井数据进行缝隙流体指示因子的试算.A井纵波速度α，横波速度β，密度ρ以及各向异性参数δ（V），ε（V）和γ如图3所示.

分析A井的纵横波速度和密度曲线，并结合各向异性参数曲线可知，该井通过两套裂缝储层（如图中圈注）.对比上下层弹性参数和各向异性参数变化，两套储层的纵横波速度和密度均有减小，各向异性参数的变化也较为明显，但变化幅度不同.

利用A井弹性参数和各向异性参数，反推计算A井各点的弹性矩阵，进而计算各点的正向差值ΔN和切向差值ΔT，结果如图4所示.

从图4中展示的正向差值ΔN和切向差值ΔT变化特征，可以进一步标定两套储层的位置和储层中裂缝的发育程度，同时表明两套储层中裂缝对各向同性背景介质的影响并不相同.

根据公式（3）计算流体指示因子，识别缝隙流体类型.

图3 A井弹性参数和各向异性参数Fig.3 Elastic parameters and anisotropic parameters of well A

图4 A井正向差值和切向差值Fig.4 ΔNandΔTof well A

如图5所示，两套裂缝储层的流体因子值并不相同.依照图1中探讨的流体因子和缝隙流体类别以及裂缝密度的关系，结合钻井资料和测井地质分析，可以得出如下结论：该井经过的第一个裂缝储层中含气，第二个裂缝储层中为油水混合；第一个储层比第二个储层的裂缝密度要大.

3.2 缝隙流体因子地震AVAZ反演

（1）实际工区井试验

利用A井的合成地震记录对缝隙流体因子的反演算法进行试算.选取拟Zoeppritz方程求解界面精确反射系数，利用45Hz的Ricker子波，依照褶积模型制作合成地震记录，并添加不同信噪比的随机噪声.方位角为0°，30°和60°、不同信噪比的合成地震记录分别如图6所示.

图5 A井流体因子变化特征Fig.5 Fluid factor variation characteristic of well A

通过反褶积提取不同信噪比，不同方位角的反射系数.按照公式（13）定义，将不同方位角反射系数做差，通过最小二乘反演方法求取裂缝正向差值ΔN和切向差值ΔT，进而求得流体因子KN／KT反演值，其结果如图7所示.

对含不同信噪比随机噪声的方位合成地震记录进行AVAZ流体因子反演，其结果对比如图8所示.

图6 不同方位角合成地震记录Fig.6 Synthetic traces of different angles

图7 不含噪声时缝隙流体因子反演值（红线）与真实值（蓝线）对比Fig.7 The comparison between fluid factor estimation result（red line）and real well log data（blue line）（No noise）

从图7和图8曲线对比可知，即使添加信噪比为1／2的随机噪声时，流体因子AVAZ反演值与测井真实值之间差别不大，而且反演结果裂缝位置明确，缝隙流体性质指示明显，满足反演要求.

（2）复杂模型试验

图8 含不同信噪比随机噪声时缝隙流体因子反演值（红线）与真实值（蓝线）对比（a）信噪比为2；（b）信噪比为1；（c）信噪比为1／2.Fig.8 The comparison between fluid factor estimation result（red line）and real well log data（blue line）with different S／N ratios（a）S／N＝2；（b）S／N＝1；（c）S／N＝1／2.

图9 逆掩断层模型的弹性参数（a）纵波阻抗；（b）横波阻抗.Fig.9 Elastic parameters of overthrust model（a）P wave impedance；（b）S wave impedance.

选取Aminzadeh等（1997）和Mulder等（2006）构建的二维逆掩断层各向异性模型进行流体因子分析和AVAZ反演试算，进一步验证流体因子AVAZ反演估测方法的适用性.同样选取拟Zoeppritz方程对二维逆掩断层模型每一道求解反射界面的精确反射系数，采用45Hz的Ricker子波，按照褶积模型制作方位角合成地震记录，在添加不同信噪比的随机噪声情况下，对合成地震记录进行弹性参数的AVAZ反演，在合理估测正向差值和切向差值的基础上实现缝隙流体指示因子的预测.

逆掩断层ΔN，ΔT和KN／KT反演结果真实值和估测值对比如图10所示，当添加随机噪声时（S／N＝2），AVAZ反演估测的ΔN和ΔT与模型真实值之间吻合较好，而且估测值的横向连续性较好，能够较好地刻画出断层的边界，同时通过比较ΔN和ΔT的数值大小可识别裂缝储层.另外，KN／KT反演值和模型真实值对比可以反映出缝隙流体特征.

4 结论和认识

当储层中发育较多垂直或近似垂直的缝隙时，储层会表现出较强的各向异性特征.而当缝隙中充填不同流体（油、气、水）时，其地震响应特征也不相同.本文主要研究了基于岩石物理的裂缝储层缝隙流体指示因子的AVAZ估测方法，从各向异性裂缝模型出发，引入可有效识别缝隙流体的指示因子，分析了不同流体充填时介质的地震响应特征，并验证了缝隙流体指示因子的AVAZ反演方法.测井数据和二维逆掩断层模型试算表明，基于岩石物理的缝隙流体因子AVAZ反演方法合理、可靠，且具有良好的抗噪性，即当对合成地震记录添加信噪比较小的随机噪声时，利用AVAZ 反演方法估测所得流体因子值与真实值仍然吻合较好.与常规流体因子的AVO反演方法相比，该方法基于岩石物理模型，在求取储层中由于裂缝存在而产生的正差值和切差值的基础上，综合研究地震振幅随入射角和方位角的变化特征，进而预测缝隙流体因子，提高了流体因子预测的精度.然而，在实际裂缝储层预测时，譬如缝洞型碳酸盐储层、缝隙发育的页岩气储层，除进行地层岩性特征的详细分析外，还要考虑其他缝隙充填物（方解石、泥，等）对缝隙流体因子的影响，着手构建适用于各种岩性储层的缝隙流体指示因子，并发展合理的AVAZ叠前反演估测方法，以便更好地进行裂缝型储层的预测和缝隙流体的识别.

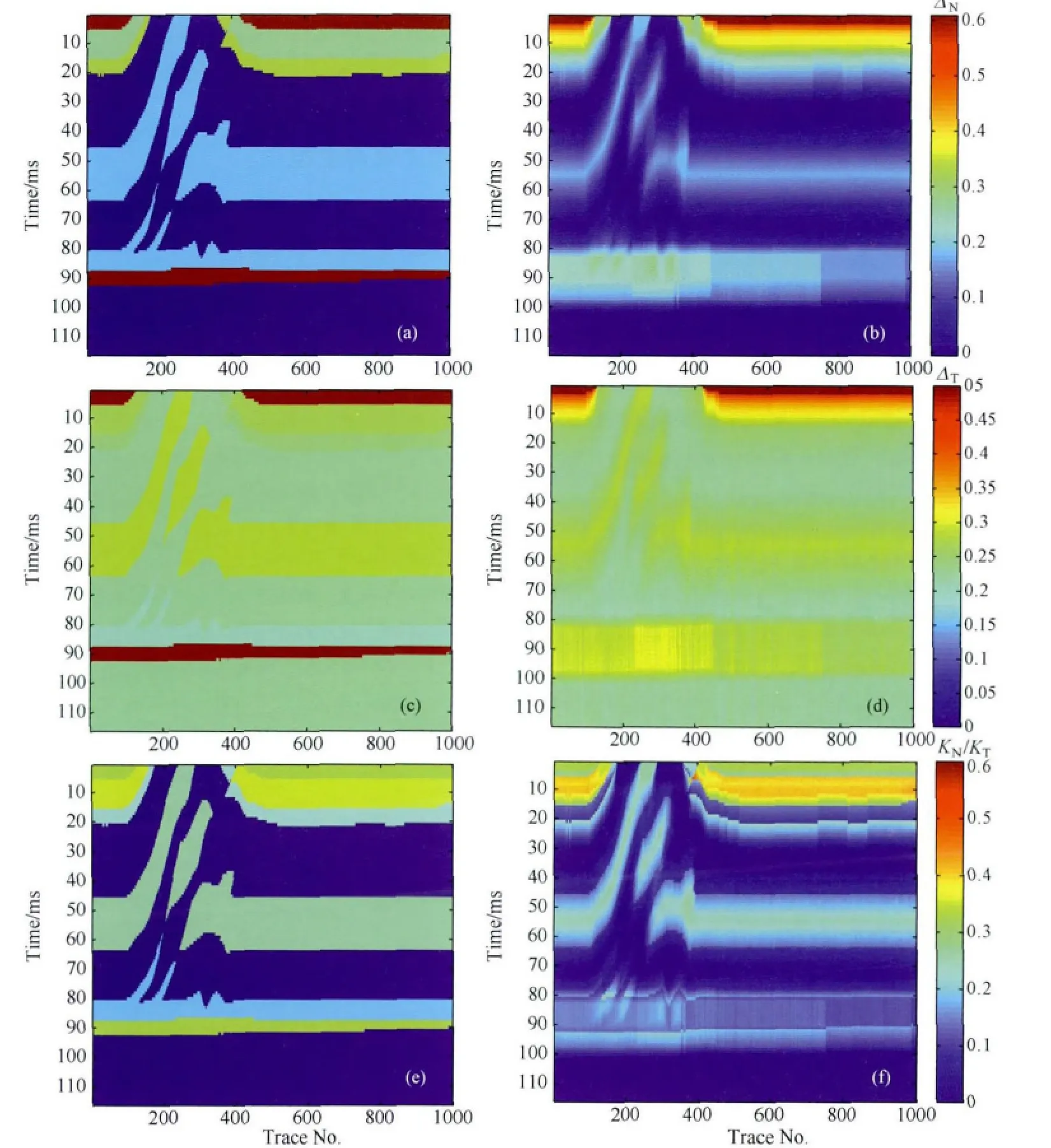
图10 添加随机噪声时ΔN，ΔT和KN／KT反演结果（S／N＝2）（a）ΔN真实值；（b）ΔN估测值；（c）ΔT真实值；（d）ΔT估测值；（e）KN／KT真实值；（f）KN／KT估测值.Fig.10 ΔN，ΔTand KN／KTestimated results comparison with true value of all CDP gathers with noise（a）ΔNtrue value；（b）ΔNestimation result；（c）ΔTtrue value；（d）ΔTestimation result；（e）KN／KTtrue value；（f）KN／KTestimation result.

Aminzadeh F，Brac J，Kunz T.1997.3-D salt and overthrust models.USA：Society of Exploration Geophysicists.

Bachrach R，Sengupta M，Salama A，etal.2009.Reconstruction of the layer anisotropic elastic parameters and high resolution fracture characterization from P-wave data：a case study using seismic inversion and Bayesian rock physics parameter estimation.Geophysical Prospecting，57（2）：253-262.

Bakulin A，Grechka V，Tsvankin I.2000.Estimation of fracture parameters from reflection seismic data-Part I：HTI model due to a single fracture set.Geophysics，65（6）：1788-1802.

Chen H Z，Zhang G Z，Yin X Y.2012.AVAZ inversion for elastic parameter and fracture fluid factor.82nd Ann.Internat Mtg.，Soc.Expi.Geophys.Expanded Abstracts，1-5.

Downton J，Roure B.2010.Azimuthal simultaneous elastic inversion for fracture detection.80th Ann.Internat Mtg.，Soc.Expi.Geophys.Expanded Abstracts，1-5.

Hsu C J，Schoenberg M.1993.Elastic waves through a simulated fractured medium.Geophysics，58（7）：964-977.

Hudson J A.1980.Overall properties of a cracked solid.Math.Proc.Cambridge Philos.Soc.，88（2）：371-384.

Kumar M，Han D H.2005.Pore shape effect on elastic properties of carbonate rocks.75th Ann.Internat Mtg.，Soc.Expi.Geophys.Expanded Abstracts，1-5.

Kong L Y，Wang Y B，Yang H Z.2012.Fracture parameters analyses in fracture-induced HTI double-porosity medium.Chinese J.Geophys.（in Chinese），55（1）：189-196.

Li F Y，Di B R，Wei J X，etal.2012.A method for estimating the width of carbonate fracture-cavern bodies.Chinese J.Geophys.（in Chinese），55（2）：631-636.

Mallick S，Craft K L，Meister L J，etal.1998.Determination of the principal directions of azimuthal anisotropy from P-wave seismic data.Geophysics，63（2）：692-706.

Mulder W A，Nicoletis L，Alkhalifah T.2006.The EAGE 3D Anisotropic Elastic Modeling Project.Vienna：68th EAGE Conference ＆Exhibition，Expanded Abstracts，1-5.

Neut J V D，Shaw R K，Sen M K.2007.Estimation of the fluid indicator from azimuthal AVO gradient variations at a fractured reservoir.77th Ann.Internat Mtg.，Soc.Expi.Geophys.Expanded Abstracts，1-5.

Peng Z M，Li Y L，Wu S H，etal.2008.Discriminating gas and water using multi-angle extended elastic impedance inversion in carbonate reservoirs.Chinese J.Geophys.（in Chinese），51（3）：881-885.

Qu S L，Zhu S W，Zhao Q，etal.2012.Analysis of seismic reflection characters for carbonate Karst reservoir.Chinese J.Geophys.（in Chinese），55（6）：2053-2061.

Ruger A.1996.Reflection coefficients and azimuthal AVO analysis in anisotropic media［Ph.D.thesis］.Colorado：Colorado School of Mines.

Schoenberg M.1980.Elastic wave behavior across linear slip interface.J.Acoust.Soc.Amer.，68：1516-1521.

Schoenberg M，Sayers C M.1995.Seismic anisotropy of fractured rock.Geophysics，60（1）：204-211.

Shaw R K，Sen M K.2006.Use of AVOA data to estimate fluid indicator in a vertically fractured medium.Geophysics，71（3）：C15-C24.

Xu S Y，Keys B.1999.Study of the coupled effect of pressure，frequency and fluid content on P-and S-wave velocities.69th Ann.Internat Mtg.，Soc.Expi.Geophys.Expanded Abstracts，1-5.

Xu S Y，Payne M A.2009.Modeling elastic properties in carbonate rocks.The Leading Edge，28（1）：66-74.

Yin Z H，Li X Y，Wei J X，etal.2012.A physical modeling study on the 3DP-wave azimuthal anisotropy in HTI media.Chinese J.Geophys.（in Chinese），55（11）：3805-3812.

Zhang C H，Qiao D W，Li S Z，etal.2011.Integration of oil and gas geophysical exploration technologies for geologically complex areas.Chinese J.Geophys.（in Chinese），54（2）：374-387.

Zhang G Z，Chen H Z，Yin X Y，etal.2012.Method of fracture elastic parameter inversion based on anisotropic AVO.Journal of Jilin University（Earth Science Edition），42（3）：845-851，871.

附中文参考文献

孔丽云，王一博，杨慧珠.2012.裂缝诱导HTI双孔隙介质中的裂缝参数分析.地球物理学报，55（1）：189-196.

李凡异，狄帮让，魏建新等.2012.碳酸盐岩缝洞体宽度估算方法.地球物理学报，55（2）：631-636.

彭真明，李亚林，巫盛洪等.2008.碳酸盐岩储层多角度弹性阻抗流体识别方法.地球物理学报，51（3）：881-885.

曲寿利，朱生旺，赵群等.2012.碳酸盐岩孔洞型储集体地震反射特征分析.地球物理学报，55（6）：2053-2061.

尹志恒，李向阳，魏建新等.2012.利用物理模型三维纵波数据分析HTI介质的方位各向异性.地球物理学报，55（11）：3805-3812.

张春贺，乔德武，李世臻等.2011.复杂地区油气地球物理勘探技术集成.地球物理学报，54（2）：374-387.

张广智，陈怀震，印兴耀等.2012.基于各向异性AVO的裂缝弹性参数叠前反演方法.吉林大学学报（地球科学版），42（3）：845-851，871.