一种基于多铁压电纳米纤维压力传感器设计*

汪海涛， 谭晓兰， 李佳玮

(北方工业大学 机电工程学院，北京100144)

0 引 言

压电式压力传感器是MEMS (micro-electro-mechanical system)器件中应用广泛的一类，其敏感材料多为块体和薄膜。国内外诸多专家学者对该领域做了大量的研究工作并取得了许多科研成果[1]。与块体和薄膜相比，悬空的多铁纳米复合纤维具有很大的长径比，可以将由压电效应引起的位移放大，从而有可能提高传感器性能。

本文将静电纺丝技术制备的取向有序的多铁纳米纤维[2]与MEMS技术制作的叉指电极、空腔硅基体很好的结合，设计了纳米压电纤维压力传感器的结构，对其工作原理进行了理论分析，得出了微压力传感器的输出电压，并对传感器的结构尺寸进行比较分析，以提高传感器性能。

1 压电纳米纤维压力传感器的结构设计

传感器由四部分组成(如图1)：铝掩蔽层、空腔硅基体、叉指电极、多铁纳米纤维。首先在硅片背面溅射铝并运用MEMS工艺刻蚀硅使之形成空腔硅杯，然后在硅杯上表面生长镍酸镧[3](LaNi03,LNO)，正面干法刻蚀LNO后形成叉指电极，最后由静电纺丝技术制备的平行纤维沉积固定在电极上，形成压电纳米纤维压力传感器，其剖视图如图2。

2 传感器的原理和理论分析

本传感器以多铁压电纳米纤维为敏感材料，其基本工作原理是利用纤维的压电效应。硅基体空腔部分形成弹性膜片，当膜片下表面受压时将产生应变和应力，叉指电极随之变形，引起纤维弯曲，从而使得纤维内部的正负电荷中心发生偏移，在表面出现极化电荷，叉指电极可将纤维产生的电荷以电压形式输出。

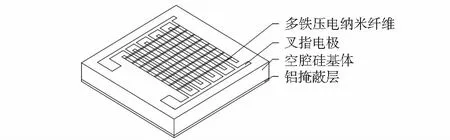
图1 传感器结构示意图

图2 传感器剖视图

2.1 弹性膜片的设计和力学分析

考虑到空腔硅杯的制作工艺，选择N型(100)硅作为硅杯膜片材料[4]。选用目标量程为0～1 kPa，硅具有良好的弹性变性特性，其弹性极限σ=8×107Pa。本文按照小挠度理论设计方形弹性膜片。将弹性膜片看作在均布载荷作用下承受横向弯矩的薄板处理，简化为周边固支的方形薄膜结构,如图3所示。

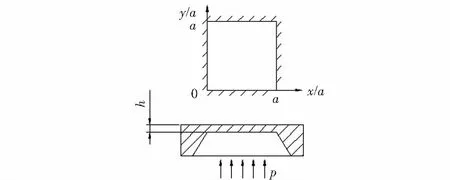
图3 周边固支的方形弹性膜片示意图

假设承受压力为p，则其小挠度弯曲理论的偏微分方程如式[5]

(1)

(2)

其中，wS,ES,μS,h分别为压力p下产生的挠度、材料的弹性模量、泊松比、膜片厚度，D为弯曲刚度。

带入周边固支的边界条件，由里兹法[6]解得其挠度曲线为

(3)

通过挠度曲线求应力表达式为

(4)

带入挠度曲线方程(3)，则正应力为

μS(x2-ax)2(6y2-6ay+a2)].

(5)

2.2 压电纤维力学分析

本传感器的有效部分为一对正、负叉指电极上搭接固定的纳米纤维，而对于两端固定、中间悬空的纳米纤维弯曲问题，可以看作是固支结构的纳米压电纤维弯曲问题[7]，以便进一步研究传感器的压电性能。图4为单根纤维与底电极组成的固支结构单元，图5为所建坐标系。

图4 单根纤维与电极组成的固支结构单元

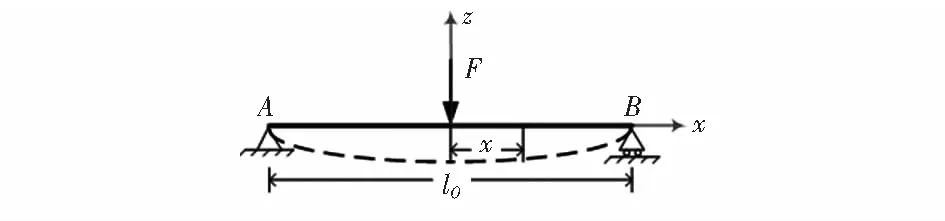
图5 固支结构单元坐标系

假设固支梁发生小变形且纤维服从胡克定律，对于纯弯曲可得挠曲线方程

(6)

带入边界条件，可以得到挠曲线为

(7)

从而可以近似得到纤维沿长度方向的变化量Δl，则单根纤维轴向应变为

1.

(8)

当y为固定值时，每段纤维就可以等效成固支结构单元，[x1.x2]段纤维受到的集中力Fo可由下式计算

Fo=A0σx|y=C=l·(x2-x1)σx|y=C.

(9)

y坐标相同的单根纤维，在[0,a]逐段积分求和即可得到单根纤维的输出电压；y坐标不同的N根纤维，每根的输出电压求和即可得到传感器的输出电压。

2.3 多铁纳米纤维的压电分析

BiFeO3多铁性材料是典型铌酸锂结构的铁电体，同时具有铁电性和铁磁性。其晶体属于三方晶系3 mm点群，根据它的介电常数、弹性常数和压电常数矩阵，可得到第一类压电方程的矩阵表示[8]。本方案只考虑多铁压电纳米纤维轴向应力与应变，根据以上分析和相关文献[9]，BFO纤维压电电压系数d33=69.3 pm/V，则单根纤维与电极组成的固支结构单元产生的电压可计算为

(10)

那么，当y=C1时，第1根纤维输出电压为

(11)

同理，当y=Cn时，第n根纤维输出电压为

(12)

2.4 传感器输出电压

综上，传感器总输出电压为

(13)

其中

(14)

3 不同结构尺寸对传感器的影响和结果分析

根据式(13)，可知压电纳米纤维压力传感器受力的作用时，其输出电压主要由纤维直径d、弹性薄膜边长a、以及电极间距、电极宽度、弹性薄膜厚度等因素决定。根据实验室工艺条件，本传感器参数设计见表1。

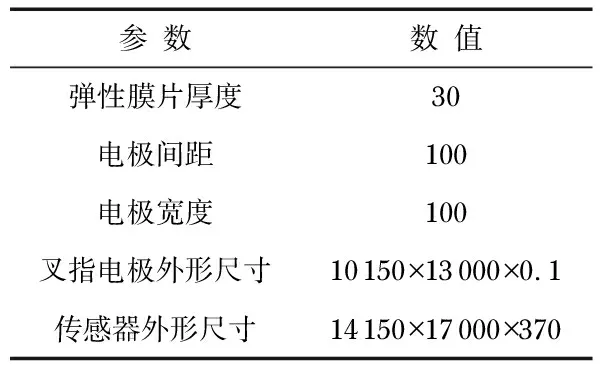
表1 压电纳米纤维压力传感器参数(μm)

本文通过对比纤维直径d、弹性薄膜边长a这2个参数的不同值，在传感器受到1 kPa均布载荷作用时，将数据分别带入式(13)。用Matlab得到计算结果:

1)当选取弹性薄膜边长a=9 000 μm，有效纤维根数为100根(纤维中心线等距间隔90 μm)，纤维直径d=0.3 ～1 μm，每段等距间隔100 nm 时，可以得到压电纳米纤维压力传感器的输出电压与纤维直径呈反比关系，如图6所示。

2)当选取纤维直径d=500 nm，纤维中心线间隔与上一组相同为90 μm时，弹性薄膜边长a=3 ～9 mm，每段等距间隔1 mm 时，可以得到压电纳米纤维压力传感器的输出电压与弹性薄膜边长呈正比关系，如图7所示。

图6 纤维直径对输出电压的影响

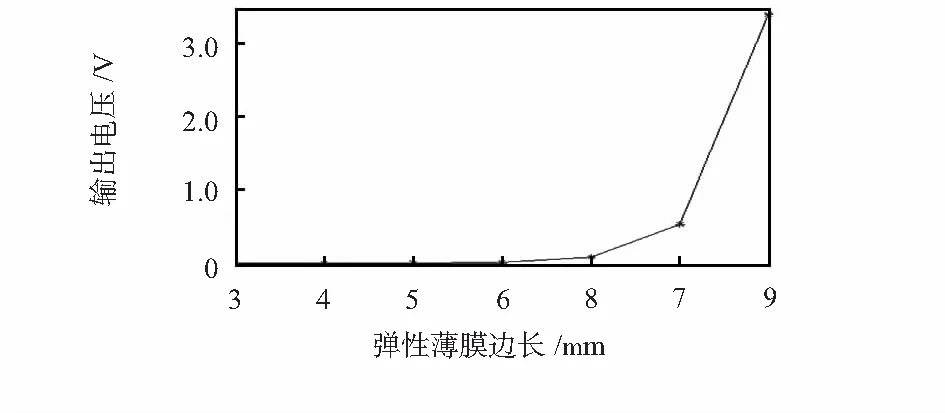
图7 弹性薄膜边长对输出电压的影响

4 结 论

本文设计了一种基于压电纳米纤维压力传感器，建立了传感器的力与输出电压转换关系。结合实际工艺条件，通过对比分析结构尺寸提高传感器输出。在弹性薄膜边长不变、纤维直径变化的情况下，可以得到压电纳米纤维压力传感器的输出电压与纤维直径呈反比关系，这与文献[10]中的ANSYS仿真分析结果一致。纤维直径越小，在纤维长度方向上的极化就越充分，因此，传感性能就越好。在纤维直径不变、弹性薄膜边长变化的情况下，可以得到压电纳米纤维压力传感器的输出电压与弹性薄膜边长呈正比关系。弹性薄膜边长越大，一方面使纤维所受应力和应变越大，另一方面增加了纤维的有效距离，从而使传感器输出电压越大。

参考文献:

[1] 张福学,王丽坤.现代压电学[M].北京:科学出版社,2002.

[2] 谢淑红.多重铁性微纳米材料的制备与表征[D].湘潭：湘潭大学，2008.

[3] 苏德志.ZnO/LNO薄膜的磁控溅射制备与性能研究[D].北京：北方工业大学，2013.

[4] 刘珍妮,谭晓兰,杨峻松.一种硅微压阻式压力传感器的研究[J].机械设计与制造,2012(1):103-105.

[5] 刘广玉.微传感器设计、制造与应用[M].北京:北京航空航天大学出版社,2008:9-10.

[6] 杨骊先.弹性力学及有限单元法[M].杭州:浙江大学出版社,2002:145.

[7] 荣英凤.BDT铁电薄膜和ZnO纳米带压电性能的测试与表征[D].湘潭：湘潭大学，2010.

[8] 王春雷,李吉超,赵明磊.压电铁电物理[M].北京:科学出版社,2009:158.

[9] Chen X,Xu S,Yao N,et al.1.6 V Nanogenerator for mechanical energy harvesting using PZT nanofibers[J].Nano Letters,2010,10(6):2133-2137.

[10] 吴爱军.压电纤维OPCM传感元件设计分析、制备与性能测试研究[D].镇江：江苏大学，2007.