交错并联Buck中耦合电感的设计
2014-09-25李祥忠王善良卢俊龙
李祥忠,朱 彬,王善良,卢俊龙
(1.深圳市中兴昆腾有限公司 广东 深圳 518000;2.中国人民解放军96623部队 江西 上饶 334000;3.哈尔滨工业大学 深圳研究生院,广东 深圳 518055)
交错并联Buck中耦合电感的设计
李祥忠1,朱 彬2,王善良1,卢俊龙3
(1.深圳市中兴昆腾有限公司 广东 深圳 518000;2.中国人民解放军96623部队 江西 上饶 334000;3.哈尔滨工业大学 深圳研究生院,广东 深圳 518055)
针对开关电源系统对功率密度等级不断提高的要求,为进一步发挥交错并联技术的优势,本文以减小输出电流纹波和改善动态特性为目标,对大占空比条件下交错并联Buck电路中的耦合电感进行了详细分析和计算。通过软件仿真验证,得出了耦合系数和占空比对电路性能的具体影响,耦合系数的取值应尽量接近-1,从而为耦合电感的设计提供了理论依据。
交错并联;耦合电感;开关电源;电流纹波
随着电子系统集成规模的不断增大,要求电源的输出电流和输出的功率越来越大。交错并联技术由于可以提高输出电流和输出功率,降低输出电流纹波以及减小滤波器和铜、铁的消耗而被广泛应用于开关电源变换器中[1]。
然而,由于磁性元件数量的增加,变换器的体积增大,限制了变换器的功率密度。因此,有必要将磁集成技术引入到交错并联变换器中以进一步改善磁件性能和提高变换器工作效率[2-4]。
此外,根据稳态和瞬态条件下电感值对变换器的影响可知:稳态条件下,电感值越大,变换器的效率越高;而瞬态条件下,电感值越小,变换器的动态响应越好。因此,要同时满足变换器工作效率和动态响应的要求,必须采用非线性电感,即电感值随电路状态而相应变化,而耦合电感具有电感值非线性的特性[5]。
本文通过分析耦合电感的磁路原理,等效电路以及耦合系数对电路的影响,以增大功率密度和减小输出电流纹波为目标,主要研究在占空比大于50%时的工作过程,设计出适用于大占空比条件下交错并联Buck电路的耦合电感。
1 两相交错并联Buck中的耦合电感分析
图1为两相交错并联Buck电路,由交错并联电路可知,功率器件均由两相并联连接构成,理论上总功率为单相功率的两倍。由于磁性器件的增加,若采用分立电感,则电路体积增大,对于多相交错并联Buck而言,电路总体体积会更大,因此,为提高功率密度,电感L1、L2应采用耦合电感形式。
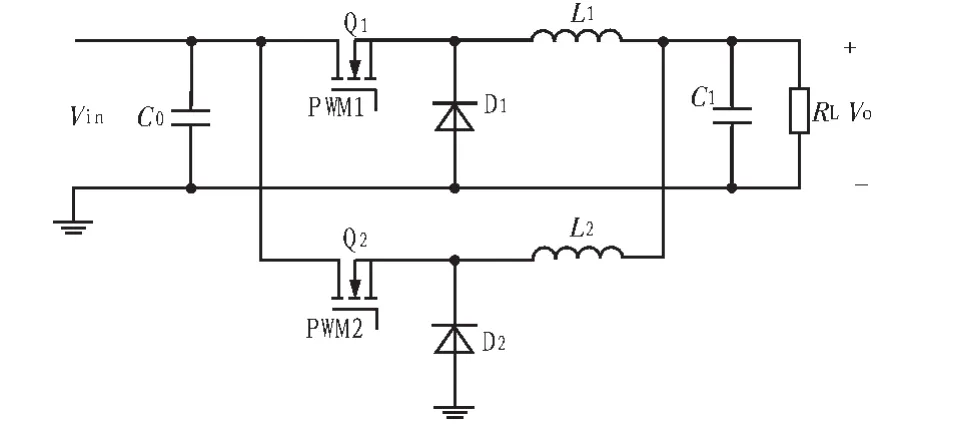
图1 两相交错并联Buck电路Fig.1 Two-phase interleaved Buck circuit
耦合电感由两种形式,即同向耦合和反向耦合,如图2所示为两种耦合电感形式及其等效电路。
图 2 中 M 为 L1与 L2的互感,v1、v2分别为电感 L1、L2两端的电压,i1、i2为流过L1、L2的电流,则根据电路理论可知:

图2 耦合电感以及等效电路Fig.2 Coupled-inductors and their equivalent circuits



如果v1与v2的关系确定,则式(2)可写成

其中,Leq为电感L1的等效电感。在一个开关周期内,v1和v2的关系是变化的,因此一个开关周期内不同时间段等效电感Leq的值也不同。但电感必须遵循伏秒平衡原则,即在一个开关周期内电感的伏秒数必须平衡。因此可根据伏秒平衡原则,计算出不同时间段电感。设Va=Vin-V0,Vb=-V0,在一个开关周期中,V1和V2有3个不同关系式。
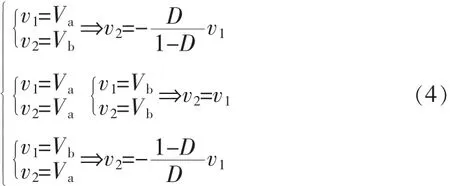
将(4)中各式代入(2)中,可得出不同时段的等效电感为
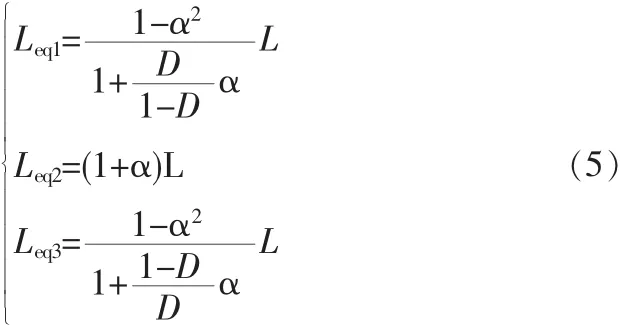
从式 (5) 可知,Leq1为当 v1>0,v2<0时 L1的等效电感,Leq3为当 v1<0, v1>0 时 L1的等效电感, 而 Leq2为当 v1=v2时L1的等效电感,如图3所示。 图中,电感电流波形i1、i2中虚线表示 L1、L2为分立电感情况下的波形,而实线为L1、L2采用耦合电感时的波形,占空比D>50%。

图3 耦合电感的电压、电流波形Fig.3 Voltage and current waveforms of coupled-inductor
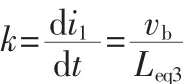
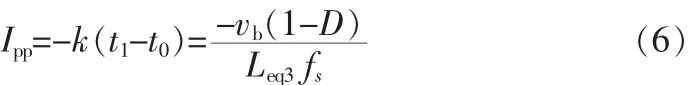
由式(6)可知,Leq3越大,稳态电流纹波越小,又根据式(5)中Leq3与耦合系数的关系可知,当时,Leq3取值更大。
动态响应可以通过电感电流的变化量Δi与ΔD的比值来表示,即
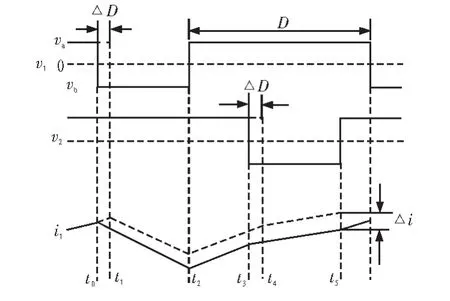
图4 瞬态变化时的波形图Fig.4 Waveforms of transient state
如图4所示为当占空比D发生微小变化时,电感电流的变化过程。当占空比变化量为时,在一个开关周期中,电感电流的变化量Δi可分为5个时间段的变化之和,即

则一个开关周期中总的电流变化量为
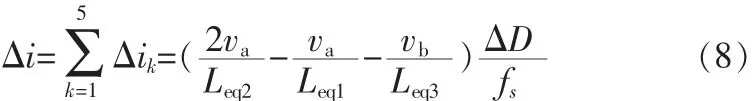
又由于稳态条件下一个开关周期中电感电流的总变化量为零,则有
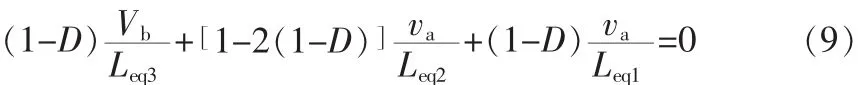
联立式(8)、(9),可解得

所以系统动态响应速度可表示为

由式(11)可知,系统动态响应速度与等效电感值Leq2成反比,即Leq2越小,响应速度越快。设Ltr为瞬态电感值,可令,Ltr=Leq2根据式(5)可知,Ltr=Leq2=(1+α)L,令 Ltr=Leq2<L,则有α<0。因此采用反向耦合的方式(α<0),可以同时增大稳态等效电感值和减小瞬态等效电感值,在减小输出电流纹波的同时可以提高动态响应速度。
2 耦合系数对电路的影响
由上述分析可知,耦合系数对输出电流纹波和系统动态性能有具体的影响,设Ltr与Lss分别为瞬态等效电感值和稳态等效电感值,则输出电流纹波和动态响应的效果可用下式表示


图5 耦合系数与电路性能的关系Fig.5 Relationship between coupling coefficient and circuit performance
3 仿真结果
在分析耦合系数对电路影响以及耦合电感工作原理的基础上,对如图1所示的两相交错并联Buck电路进行仿真。
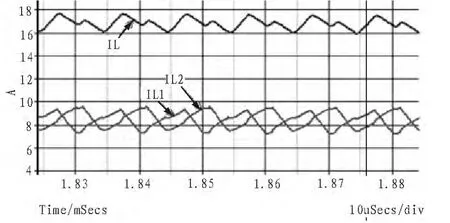
图6 同相耦合下电流波形Fig.6 Current waveforms when directly coupled
图6为在同相耦合情况下,占空比D=70%,开关频率fs=100 kHz,Vin=100 V,RL=4 Ω,两路驱动信号延时 4 μs,耦合系数 α=0.9且电感值 L1=L2=105 μH 时电感 L1、L2的电流 IL1、IL2以及两者之和IL的波形。从图中可看出,耦合电感采用同相耦合形式时,电感电流IL1、IL2的纹波均较大。且IL1与IL2之和IL的纹波也大于1 A。
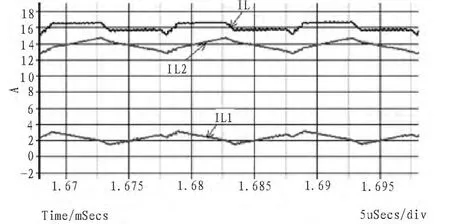
图7 反向耦合下电流波形Fig.7 Current waveforms when inversely coupled
图7为反向耦合情况下,耦合系数α=-0.9且其他条件均与图6中相同时的电流波形。从图7可看出,反向耦合时,电感L1、L2的纹波均比图6中小很多,且IL1、IL2之和 IL的纹波小于0.2 A,但在两路驱动信号同时变化时也存在一定范围内的波动,因此须根据实际应用场合再加以改善。
4 结 论
根据文中对耦合电感的分析及推导可知,耦合系数与占空比的大小对交错并联Buck电路性能有重要影响。当占空比为50%时,理论上输出电流纹波可以达到零,但在很多应用场合,电路的占空比有可能大于50%,如空间电源充电系统等,因此,根据本文研究内容,在大占空比情况下,要达到减小输出电流纹波的目的,耦合电感应采用反向耦合的形式,且耦合系数应尽量取接近-1而又不等于-1的值。
[1]徐立刚.适用于交错并联电路的新型耦合电感[D].南京:南京航空航天大学,2009.
[2]陈乾宏,阮新波,严仰光.采用磁集成技术的高效率、低压输出正反激变换器[J].电工技术学报,2002,16(1):53-58.CHEN Qian-hong,RUAN Xin-bo,YAN Yang-guang.High efficiency,low positive and negative output forward and flywardconverterbasedonIntegrated Magnetics[J].Transactions of China Electrotechnical Society,2002,16(1):53-58.
[3]Wei J,Xu P, H-P,et al.Comparison of three topology candidates for 12V VRM[J].Proc.IEEE APEC,2001(1):245-251.
[4]Chen W,Lee F C,Zhou X,et al.Integrated planar inductor scheme for multi-moduleinterleaved quasi-squarewave(QSW) DC/DC converter[J].Proc.IEEE PESC,1999(2):759-763.
[5]Sefa I,Balci S,Altin N.Comprehensive Analysis of Inductors for an Interleaved Buck Converter[C]//15th International Power Electronics and Motion Control Conference, Serbia,2012:551-557.
[6]Wong P.Performance improment of multi-channel interleaving voltage regulator modules with integrated coupling inductors[J].IEEE Transactions on Power Electronics,2001,16 (4):499-507.
Design of coupled inductor in interleaved Buck
LI Xiang-zhong1, ZHU Bin2, WANG Shan-liang1, LU Jun-long3
(1.ZTE Quantum Co., Ltd, Shenzhen 518000, China; 2.Unit 96623 of PLA, Shangrao 334000, China;3.Shenzhen Graduate School, Harbin Institute of Technology, Shenzhen 518055, China)
In order to solve the problem of power density in switching power supply and further develop the advantages of interleaving techniques,this paper carries out a detailed analysis and calculation on the coupled inductor of Interleaved Buck circuit with the target of reducing the output current ripple and improving the dynamic characteristics.By studying the principle of circuit and simulating in software,a conclusion on how to determine the coupling coefficient and the duty cycle of the specific impact on circuit performance is gotten,it is important that the value of the coupling coefficient is close to-1.
interleaved; couple-inductor; switching power supply; current ripple
TN712
A
1674-6236(2014)15-0116-03
2014-02-24 稿件编号:201402152
深圳市科技创新计划项目(CXZZ20120615163423014)
李祥忠(1969—),男,江苏连云港人,硕士,中级工程师。研究方向:电力电子技术。
