γ射线旋转调制器成像系统的研制

魏 星 王 锋 王 英 肖无云 艾宪芸 张 斌 徐红鹃 张 磊 马新华

（防化研究院 国民核生化灾害防护国家重点实验室 北京 102205）

γ射线成像技术引入核辐射监测领域后，在发现热点、确定沾染区域、定位放射源、辐射防护评估等方面得到广泛应用，具有巨大的技术优势。以非接触方式在一定距离外获取 γ射线源的精细图像，这是其他核辐射监测技术无法实现的。为满足当前核辐射监测任务对高性能γ射线成像系统的需求，提出了研制一种探测效率高、能量响应范围宽、能区分不同放射性核素图像的γ射线成像系统。

γ射线无法聚焦，因此人们发明了各种非聚焦技术来实现对γ射线源的成像。其中基于空间编码的编码孔(Coded Aperture, CA)成像技术[1]因其高灵敏度、高分辨率的优点，成为目前核辐射监测中应用最多的成像技术。为满足 Nyquist采样定律，对CA成像系统探测器位置分辨率的基本要求是不能超过小孔尺寸的一半，因此一个CA系统通常需要大量读出通道以达到足够的位置计算精度。在像距一定的情况下，CA系统的角度分辨率由探测器位置分辨率决定。因此，保持角度分辨率的同时扩展探测器面积，必然导致读出通道数急剧增加。这意味着整个系统的复杂度和成本大大提高，对所有通道的一致性校正等工作也变得非常困难。CA系统的另一个缺点是探测器厚度受限制，无法提高对高能射线的探测效率。这是因为高能射线在探测器中的平均自由程更大，如果探测器较厚，斜入射光子就容易跨过像素边界发生作用，造成像素间串扰，引起图像模糊。为克服CA系统存在的这些问题，提出研制基于旋转调制器(Rotating Modulator, RM)成像技术[2]的γ射线成像系统。这是因为RM成像技术是一种时间调制成像技术，在时间域超采样，可以重建超过系统几何角度分辨率的图像。因此，RM系统可选尺寸更大的探测器，达到和CA系统相当的角度分辨率。又由于RM系统采用独立的非位置灵敏探测器，不存在像素间串扰，因此可以增加探测器厚度以提高对高能射线的探测效率。

1 RM技术简介

RM 成像系统构成主要包括一个栅条状旋转准直器和一个非位置灵敏探测器阵列，其角度分辨率由栅条宽度和像距决定[3]。准直器旋转过程中，入射γ射线会在探测器平面形成栅条阴影。因为栅条宽度等于探测器直径，因此阴影对探测器入射面的遮挡比例在0%−100%变化，又因为准直器具有180°对称性，因此变化周期为p。这使得探测器输出呈现以p为周期的起伏变化，这一过程即时间调制过程。假设目标空间划分为N个像素点，S(n)表示目标空间第n个像素的强度；系统包含D个探测器，d表示探测器序号；采样时间周期为T，单位s，整个测量过程持续M个时间周期，Od(m)表示第m个时间周期内探测器d的计数。假设系统传递函数为P，则目标空间第n个像素在第m个时间周期向探测器d的传递系数为Pd(n,m)。为简化公式书写，约定式(2)中d的取值范围是1−D，n和n¢的取值范围是1−N，m的取值范围是1−M。由此得到调制过程的离散数学表达式写为：

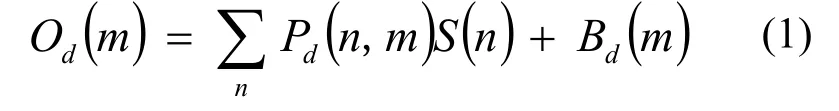
式中，Bd(m)是探测器d在第m个时间周期的本底计数。系统参数已知的情况下，可以预先计算Pd(n,m)[4]。因为准直器旋转的周期性，因此将时间轴映射到准直器转角坐标来计算其归一化值。

图像重建的过程就是根据式(1)求解 S(n)的过程。求解的第一步是通过互相关将时间域的测量数据Od(m)转换到图像空间：

式(3)是典型的投影方程，A可看做大小为N×N的传递矩阵，A的计算由式(3)给出。

互相关图像C中，在真实源图像周围出现波纹状起伏边缘，因此需要进一步求解式(2)来消除这些边缘。迭代法适合于求解式(2)。受统计噪声影响，代数迭代算法容易出现噪声放大，在重建图像中产生伪像，因此提出用基于泊松统计模型的极大似然-期望最大化(Maximum Likelihood Expectation Maximization, MLEM)迭代算法[5]重建图像。MLEM算法迭代公式为：

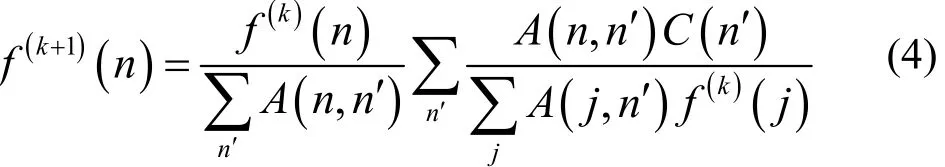
根据探测器计数，可以反推出目标空间一点的源强。假设测量过程中本底计数率恒为b，min−1；没有准直器情况下，位于像素n的源在探测器d处引起的计数率恒为s，min−1。设：

根据式(6)求出计数率 s，假设被测目标距离较远，则源强S(n)可由式(7)计算：

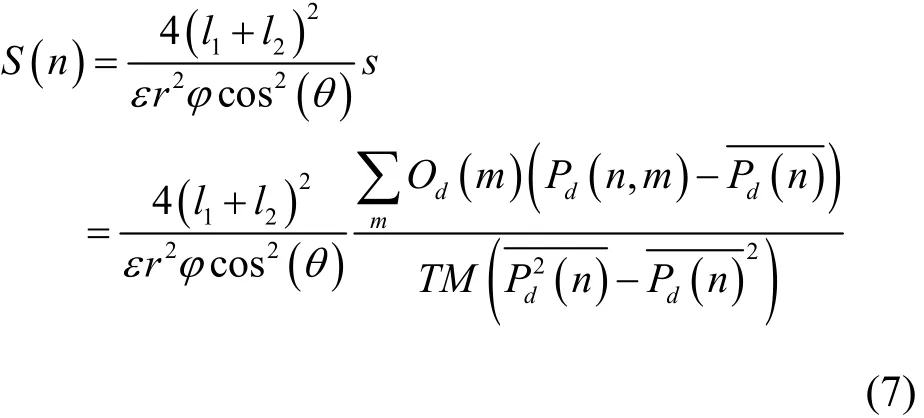
式中，l1是物距；ε是探测效率；θ是源所处位置的极角；r是探测器入射面半径；φ是对应能量光子的产额。

2 样机设计

根据实际条件，RM样机研制选用了7个滨松的CH292 NaI(Tl)探测器。该型号探测器灵敏区尺寸为Φ40 mm×40 mm。7个探测器排列方式可参考文献[3]。1号探测器位于旋转轴与像面交点，即探测器阵列的中心；2−7号探测器间隔60°均匀排列于1号探测器四周，其与 1号探测器的圆心距离均为7.1cm。这种排列可以最大化利用整个视场范围，并使系统对目标空间的灵敏度更加均匀。准直器由8条宽4 cm、厚1 cm的铅条组成。铅条平行排列，间隔4 cm。每个铅条由2 mm铝包裹。准直器旋转中心位于第4条和第5条栅条之间，计算出准直器旋转半径为30 cm。由此确定铅条长度为60 cm。所有铅条固定于两个铝制圆环（内环）之间，两个铝制圆环通过钢珠方式与另两个铝制圆环（外环）耦合，外环再与铝合金框架固定连接。这样，内环就可带动铅条转动，内环的转动由一个步进电机驱动。准直器平面和探测器平面间距离80 cm，样机的几何角度分辨率约2.9°。

样机的电子学和软件部分采用自主研发方式。设计了7通道读出电路。各通道可循环读出设定时间采样周期内的计数值。时间采样周期在1−108ms可调。为验证该成像系统具有能量分辨能力，能够获取不同放射性核素的图像，采用了自主研发的4 k道数字化多道分析器(Digital Multi-Channel Analyzer, DMCA)。此外，电路部分还集成了步进电机控制卡和驱动器。读出电路通过以太网口与计算机通信，电机控制器则通过PCI口与计算机通信，相应地开发了专用的计算机数据采集处理软件和电机控制软件。为避免长期转动过程中，可能出现的皮带轮打滑以及电机转速不均匀，数据采集电路设计了霍尔开关接口。在准直器外环上安装了一个固定的霍尔开关，在内环上安装了一个磁铁。这样，内环每旋转一周，磁铁会触发霍尔开关一次，据此对内环旋转位置和时间的关系进行校正。最后，在样机前方安装了可见光摄像头，用于捕捉可见光图像。样机实物如图1所示。

图1 样机实物图Fig.1 Photograph of the RM prototype.

3 实验

3.1 能量分辨率

首先对探测器能量分辨率进行测量。在没有准直器情况下，测量了活度为6.29×104Bq的137Cs源和活度为 5.8×104Bq的60Co的混合能谱，其中 1号探测器测得的能谱如图 2，两种核素的特征峰非常明显。计算得到探测器能量分辨率为7%@662keV。

图2 实测能谱Fig.2 Measured spectrum.

3.2 探测效率

为了保证7路输出数据的一致性，需对7个探测器的效率进行一致性校正。这里定义绝对探测效率为：

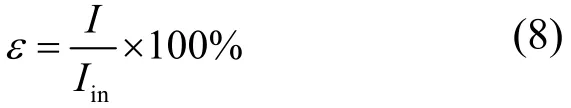
式中，I是记录的粒子数，Iin是入射粒子数。效率测量采用一枚活度为1.85×108Bq的137Cs密封源。其结构符合 GB/T 13366-2009规定，活性区尺寸Φ4mm× 4mm，外壳尺寸Φ8 mm×10 mm。

首先测量了7路本底输出，再在没有准直器的情况下对置于6 m外的源进行测量。其中本底测量时间2 h，源测量时间30 min。测得的计数率和探测效率如表 1所示，7个探测器平均探测效率为22.2%。

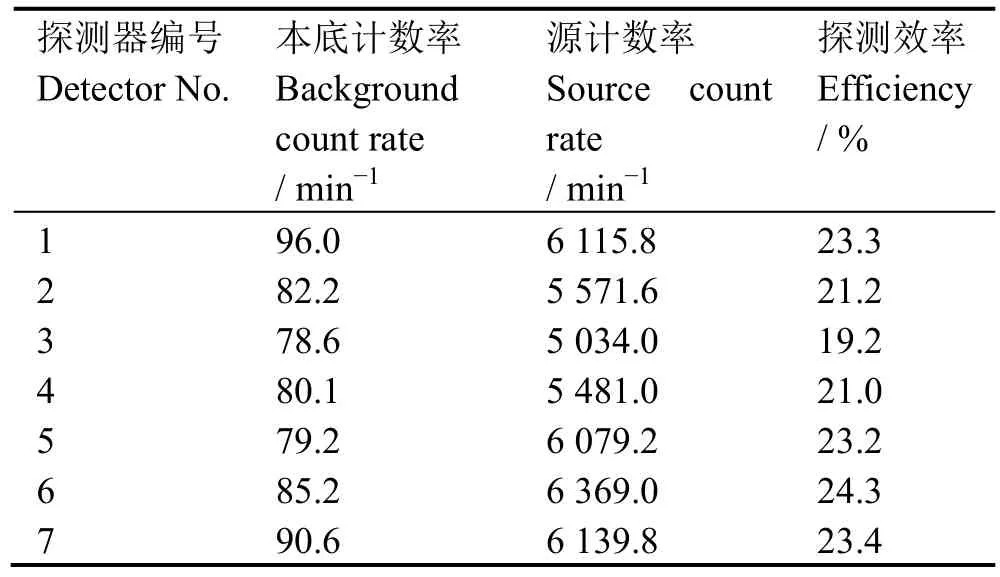
表1 探测器计数及效率Table 1 Detectors count rate and efficiency.

3.3 灵敏度

RM系统的归一化灵敏度定义为：

式中，η是超分辨因子，对RM系统，η=1。式中的取平均值表示在时间域上的平均。根据式(9)计算可知：在约±14.6°范围内，平均灵敏度约 0.31，超过这个范围后，受调制的探测器数量减少，灵敏度下降，直至没有探测器受调制，灵敏度下降为 0。因此该样机有效视场范围约±14.6°。

3.4 成像实验

成像实验和效率测量使用同一放射源。该样机对置于6 m外的放射源进行成像测量，放射源位于极坐标 θ=3°、方位角 ψ=60°。准直器转速0.86r·min−1，时间采样周期 200 ms，共测量 300 s，图3(a)是2号探测器随时间变化的输出曲线。从探测器输出数据中截取了整圈的部分，映射到准直器转角坐标后，有效测量时间为256 s，输出曲线如图3(b)。图4是用MLEM算法重建的图像。

为验证辐射图像中源的位置是否准确，将辐射图像与可见光图像用加权平均法[6]进行融合。图 5是将源置于不同位置用同一配准矩阵得到的两幅融合图像，该配准矩阵通过基于外部控制点的方法[7]得到。图5中辐射图像能够很好地与实际位置匹配，证明了重建源位置的准确性。

对重建图像实际能达到的角度分辨率进行了测试。测试采用两枚活度为1.85×108Bq的137Cs密封源，源的结构尺寸与效率测量所用的源相同。在6 m距离处，将两个源逐渐靠近，得到相应的重建图像。以峰的半高宽处为分辨标准，当两个源间隔 2°时（距离20.9 cm），两个峰的半高宽处相互分开，当两个源间隔1.8°时（间隔18.9 cm），两个峰的半高宽处相互重叠。图6是重建得到的两个点源的峰。

图3 2号探测器随时间输出曲线(a)和随转角变化曲线(b)Fig.3 Plot of detector 2 output (counts) against time (a) and rotating angle (b).

图6 两个点源的重建峰间隔：(a) 2°，(b) 1.8°Fig.6 Reconstructed peaks for two point sources.Separation in angle: (a) 2°, (b) 1.8°

3.5 源强计算

将放射源置于不同距离，测量 5次，反推得到的源强见表2。

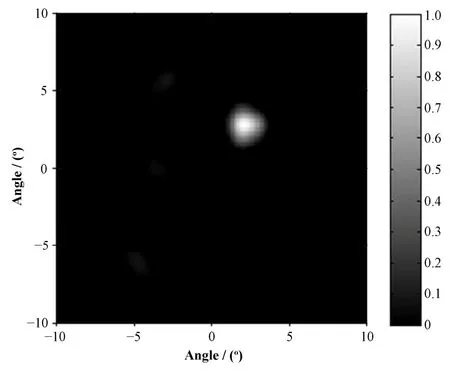
图4 MLEM算法的点源探测重建图像Fig.4 Reconstructed image of a point source by MLEM.

表2 源强计算Table 2 Calculated source intensity.

图5 融合图像Fig.5 Superimposed images.

4 结语

RM成像技术是一种时间调制的γ射线成像技术。与采用CA技术的成像系统比较，RM系统可以采用更厚的探测器而不存在像素间串扰问题，因此探测效率更高，有更宽的能量响应范围。此外，RM 系统能够同时完成能谱测量和成像测量，具有分辨不同放射性核素强度分布图像的能力。通过超分辨重建图像，RM系统能够达到和CA系统相当的角度分辨率。

研制的RM成像样机完成了对RM成像技术的验证。样机采用铅制旋转准直器和NaI(Tl)探测器阵列，可同时测量能谱和放射性核素强度分布图像，能量分辨率达到7%@662 keV。用MLEM算法重建图像能分辨间隔2°的两个点源。作为验证样机，其性能仍有很大的提高空间，例如用LaBr3(Ce)探测器以提高探测效率和能量分辨率。用钨合金材料以减少准直器厚度，减少穿透射线成份和图像重建过程中引入物理约束条件等。

1 Jean in 't Zand. Coded aperture camera imaging concept[OL]. http://astrophysics.gsfc.nasa.gov/cai/coded_intr.html, 1996

2 Durouchoux P, Hudson H, Hurford G, et al. Gamma-ray imaging with a rotating modulator[J]. Astronomy and Astrophysics, 1983, 120(1): 150−155

3 魏星, 王锋, 肖无云, 等. 一种旋转调制器成像技术研究[J]. 核技术, 2014, 37(2): 020401 WEI Xing, WANG Feng, XIAO Wuyu, et al. Study on rotating modulator imaging technique[J]. Nuclear Techniques, 2014, 37(2): 020401

4 Dadurkevicius V, Ralys D A. Modulation patterns of astronomical imaging system based on rotating grids[J].Astrophysics and Space Science, 1985, 113: 233−247

5 Shepp L A, Vardi Y. Maximum likelihood reconstruction for emission tomography[J]. IEEE Transaction on Medical Imaging, 1982, MI-1: 133−122

6 郭佳. 红外与可见光图像融合技术的研究[D]. 西安:西安工业大学, 2009 GUO Jia. Research on fusion technology of infrared and visible image[D]. Xi'an: Xi'an Industrial University, 2009

7 陈显毅. 图像配准技术及其MATLAB编程实现[M]. 北京: 电子工业出版社, 2009 CHEN Xianyi. Image registration technology and its MATLAB programming[M]. Beijing: Publishing House of Electronics Industry, 2009