酒后驾车安全临界值的数学模型分析

程红萍

（西安欧亚学院 陕西 西安 710065）

酒后驾车安全临界值的数学模型分析

程红萍

（西安欧亚学院 陕西 西安 710065）

针对日常生活中人们喝酒方式的不同即短时间内快速喝酒、在一定时间内慢速喝酒、间隔一定时间快速喝等量的酒，通过建立不同的数学模型，用MATLAB软件求解得出在不同情况下饮用不同量的酒后，血液中酒精量随时间变化的函数关系式，并通过具体的实验数据，给出酒后司机安全驾车的驾驶时间。

酒后驾车；安全临界值；数学模型；驾驶时间

随着科学的发展，社会的进步，私家车越来越多，交通事故也越来越多，自2000年以来每年因交通事故死亡的人数均在10万左右[1]。我国目前万车死亡率为7.6，日本以及欧美一些发达国家，万车死亡率平均控制在2—3之间。这一数字的背后，酒后驾车为其中第一大元凶。据资料显示，2008年因酒后驾车发生交通事故死亡人数18 371人[2]，如果将这一年单列出来计算，除以365天，平均每天死亡50人；乘以4年，每4年死亡的人数为73 484人，已超过在“5·12”汶川地震中的死亡人数6.9万；乘以14年，每14年死亡的人数为257 194人，已超过了1976年在唐山地震中死亡的人数24.2万人。2009年8月15日以后一个月的严厉整治酒后驾驶交通违法行为专项行动结果显示：全国共查处酒后驾驶违法行为65397起，其中醉酒驾驶10 711起[3]，占查处总数的16.4%；因酒后驾驶引发交通事故320起，死亡118人，受伤351人。世界卫生组织另外数据显示，在发展中国家，每33分钟就会有一人死于饮酒有关的交通事故。

针对这些严重的道路交通情况，国家质量监督检验检疫局2004年5月31日发布了新的《车辆驾驶人员血液、呼气酒精含量阈值与检验》国家标准，新标准规定，车辆驾驶人员血液中的酒精含量大于或等于20毫克／百毫升，小于80毫克／百毫升为饮酒驾车（原标准是小于100毫克／百毫升），血液中的酒精含量大于或等于80毫克／百毫升为醉酒驾车（原标准是大于或等于100毫克／百毫升）[4]。而且医学研究表明，100毫升血液含酒精40毫克，行动笨拙；60毫克，喋喋不休；80毫克，情绪激动，反应迟钝；120毫克，疲倦、瞌睡；200毫克，大小便失去控制；400毫克，昏迷；600毫克，死亡。应如何处理饮酒驾车问题，这与我们每个公民生命安全息息相关，当一个司机喝酒之后，如果能够预测自身血液中酒精含量在不同时间内的含量，那么他就可以选择安全的驾车时间，不仅不会违犯交通法规，而且还可以减少交通事故。目前针对这一实际问题，大多数[5]只是从酒精在人体内什么时间达到高峰，没有给出喝完酒后什么时间开车安全，以及想安全开车，最多能喝多少酒。本文主要研究在时间以及其他诸多因素的影响下，建立相应的数学模型，得到酒精在血液中的浓度变化函数关系式，并通过具体案例应用，为酒后司机驾车选择安全的驾驶时间以及司机根据自己的时间安排，确定喝多少酒开车是安全的。

1 模型分析、建立及求解

1.1 基本假设

1）人的胃肠的体积、体液的体积不变；

2）酒精的转移过程为3个过程: 酒精、胃肠、体液、体外；

3）从肠胃到体液的转移速度与酒精量成正比；

4）排出的速度与体液中的酒精量成正比；

5）人体血液和体液中的酒精浓度相同；

6）在较短时间内喝酒的情况下酒精量是瞬间进入胃里的；

7）在较长一段时间内喝酒的情况下酒精量是匀速进入胃里的。

1.2 符号说明

t（小时）：时刻

x(t) ：t 时刻胃肠中的酒精量（毫克）

y(t) ：t 时刻体液中的酒精量（毫克）

a ：酒精从胃肠到体液的转移系数

b ：酒精从体液到体外的排出系数

v ：体液的体积（百毫升）

f ：从口进入胃肠的酒精量（毫克）

c(t) ：t 时刻体液中的酒精含量（毫克/百毫升）

1.3 模型的建立与求解

当人们喝酒时，酒精（即乙醇）首先进入胃，然后吸收入血液，随着血液扩散到全身的器官和组织中，这样不断地被吸收、代谢和排出。这个过程可简单表示为：

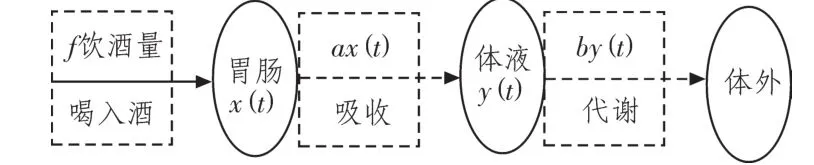
根据日常生活中人们喝酒方式的不同即短时间内快速喝酒、在一定时间内慢速喝酒、间隔一定时间快速喝等量的酒，可建立不同的数学模型，并得出在不同情况下体液中酒精浓度随时间变化的关系式。

1.3.1 短时间内快速喝酒

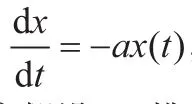
有模型I：

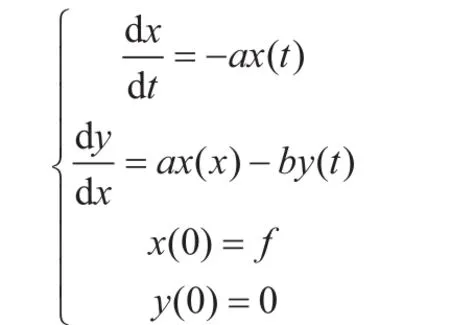
用MATLAB软件解此微分方程组可得

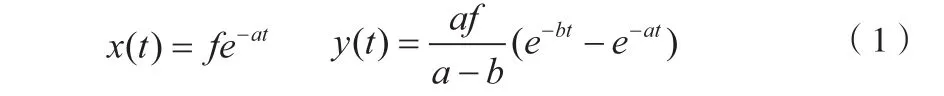
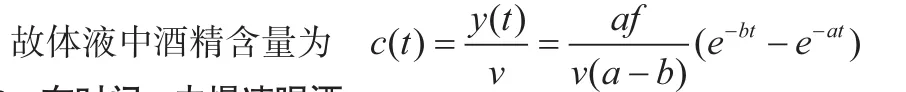
1.3.2 在时间τ内慢速喝酒

模型Ⅱ-1：0≤t≤τ（匀速喝酒）

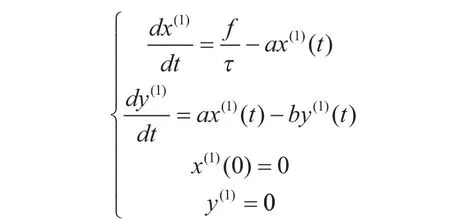
用MATLAB软件解之得

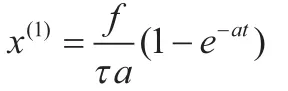
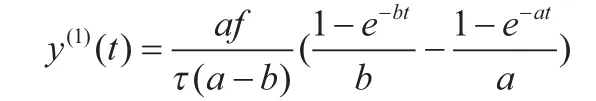
体液中酒精含量为

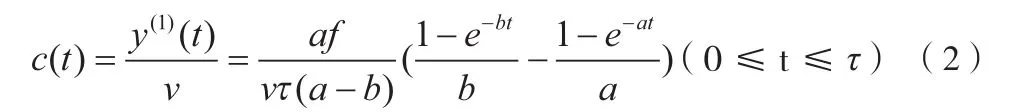
模型Ⅱ-2：t ＞τ（从喝完酒到t时刻）

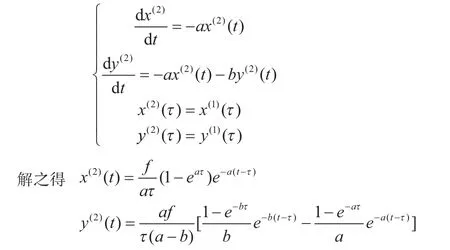
体液中酒精含量为

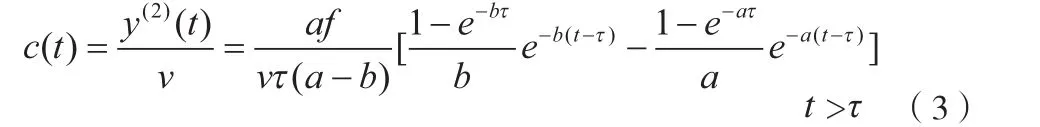
1.3.3 每T小时快速喝等量酒

以第i次喝酒的瞬间作为起始时刻，t小时后,胃肠中的酒精量记为xi(t)，体液中的酒精量记为yi(t)

模型Ⅲ

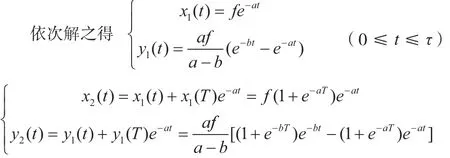
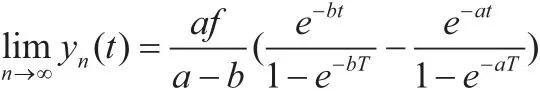
故体液中酒精含量为

2 模型的应用

经查可得如下数据[4]：人的体液占人的体重的65%～70%，其中血液只占体重的7%左右。

实验测得体重约70千克的某人在短时间喝下2瓶啤酒后，隔一定时间他的血液中酒精含量（毫克/百毫升）的数据如表1所示。

表1 血液中酒精含量（毫克/百毫升）Tab.1 Blood alcohol content (mg / one hundred milliliters)

根据国家标准，我们可知人体液中酒精含量c(t)＜20为安全驾驶。根据c(t)＜20结合前面的①、③、④式，可以算出：若打算在喝完酒t小时后开车不犯规，每天应喝多少酒即f为多少；若打算每天喝酒量为f，那么t小时后开车就较为安全。

以④式为例：若取T=24 , a=2.026 , b=0.154 ，v=70·65%·7% =3.185 , c(t)＜20可得到下表2所示。

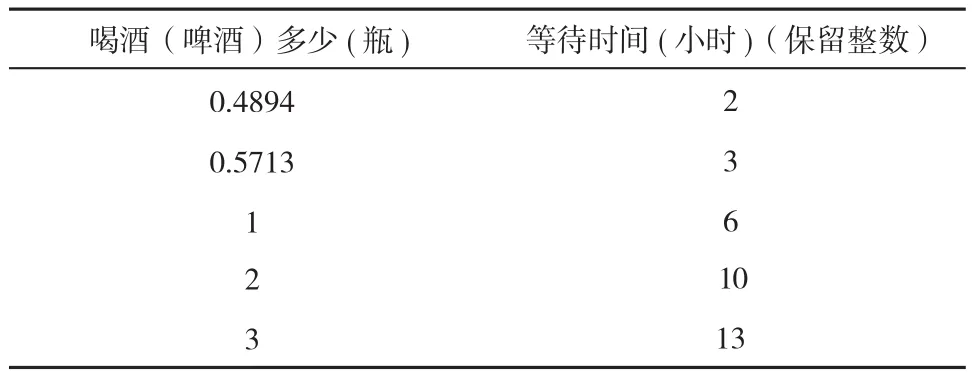
表2 喝酒量与等待时间Tab.2 Alcohol consumption and waiting time

从表2可知:

1）司机可根据自己喝酒的多少，确定酒后多少小时开车是安全的。若喝完0.489 4瓶啤酒，则安全临界值为2小时，即2小时后开车安全；若喝完0.571 3瓶啤酒则安全临界值为3小时，即3小时后开车安全；若喝完1瓶啤酒则安全临界值为6小时，即6小时后开车安全；若喝完2瓶啤酒则安全临界值为10小时，即10小时后开车安全；；若喝完3瓶啤酒则安全临界值为13小时，即13小时后开车安全。

2）司机也可根据自己的时间安排，确定喝多少酒是安全的。若喝完酒2小时后开车，喝酒的安全临界值为0.489 4瓶啤酒；若喝完酒3小时后开车，安全临界值为0.571 3瓶啤酒；若喝完酒6小时后开车，安全临界值为1瓶啤酒；若喝完酒10小时开车，安全临界值为2瓶啤酒；若喝完酒13小时后开车，安全临界值为3瓶啤酒。

3 结 论

文中对人在饮酒后血液中的酒精含量的变化过程建立了数学模型，进行了数理分析，得出在不同喝酒方式下(短时间内喝酒和较长时间内连续喝酒)体液中酒精浓度随时间变化的关系式以c(t)，从而司机可根据自己的具体情况，选择相应的c(t)关系式，来判断喝酒后安全驾车的时间以或者喝酒者根据自己的时间安排来判断喝酒的量。

此外，还可以扩大模型的应用外延，根据血液浓度的函数，确定报案时司机血液中的酒精含量以及从肇事到报案的时间间隔，即可计算出肇事时司机体内血液中的酒精含量。从而为交通部门确定肇事者是否为饮酒驾车提供很好的依据。

[1] 东方网,吴琦幸.美国的交通事故死亡率为何低[EB/OL].(2013-3-3).http://www.chinahighway.com/news/2007/209276.php.

[2] 熊永明.醉酒驾车行为“入刑”的必要性 [J].山西省政法管理干部学院学报,2010,23(1):96-97.

XIONG Yong-ming. Drunken driving behavior“into the sentence”the necessity of [J].Shanxi Politics and Law Institute, 2010,23(1):96-97.

[3] 徐伟,林艳.酒后驾车行为严查之下仍时有发生,专家热议是否增设危险驾驶罪[N].法制日报,2009-9-24.

[4] 2004年全国大学生数学建模竞赛C题[EB/OL].http://wenku.baidu.com/view/1fb841d649649b6648d74741.html.

[5] 王新华.酒后驾车问题的数学模型[J].深圳职业技术学院学报,2005(2):24-27.

WANG Xin-hua. Drunk driving mathematical model[J].Shenzhen Vocational and Technical College, 2005(2):24-27.

[6] 万正杨.2005-2011年涉嫌酒后驾车交通肇事人员血中乙醇含量结果分析[J].公共卫生与预防医学2013,4(2):108-110

WAN Zheng-yang.Persons suspected of Drunk driving Traffic Accident Analysis of blood alcohol content[J].Public Health and Preventive Medicine, 2013,4(2):108-110.

Mathematical model analysis of the safety threshold of driving after drinking

CHENG Hong-ping
（Xi'an Eurasia University, Xi'an 710065, China）

Based on the assumptions of factors affecting the alcohol content in blood，this paper contrives a differential equation model of the blood alcohol content for both a short period drinking alcohol and a long period drinking alcohol.Using Mtlab software for working out differential equations, using method of least-squares fitting of test data to determine the function parameter values, calculating the short time and long time drinking alcohol content in blood.By specific experimental data, gives safe driving drunk driver driving time.

drunk driving; safety threshold; differential equation model; driving time

TN98

A

1674-6236(2014)03-0091-03

2013–05–31 稿件编号：201305311

陕西省科技厅自然科学基金项目(2012JM1015)

程红萍(1971—)，女，陕西大荔人，硕士，讲师。研究方向：高等数学、数学建模。