分布式MIMO系统小区平均遍历容量分析

崔 磊，蔡 俊

（河海大学 江苏 南京 211100）

分布式MIMO系统小区平均遍历容量分析

崔 磊，蔡 俊

（河海大学 江苏 南京 211100）

针对分布式MIMO系统的圆形小区平均遍历容量展开研究。文章首先建立了包含快衰落、阴影衰落和路径损耗的复合衰落信道模型; 然后，对分布式天线采用覆盖式（BT）传输策略，并在高信噪比条件下，导出给定移动台位置时，区上、下行点对点链路遍历容量表达式。最后，考虑移动台在小区内任意分布特点，进一步推导出小区平均遍历容量闭合近似表达式。仿真结果表明,所推导的近似表达式可很好的反应系统的实际性能。导的近似表达式可很好的反应系统的实际性能。

分布式MIMO系统；复合信道；小区平均遍历容量；任意分布

随着无线通信的快速发展，分布式MIMO系统（DMIMO）以其覆盖范围广、功率消耗低等特点逐渐成为当前研究的热点。相比传统的集中式MIMO系统（CMIMO），DMIMO系统可根据用户的需求将天线放置在不同的地理位置，通过减小基站与用户间的距离，改善网络系统性能。大量研究表明，DMIMO系统不论在提高系统容量、提高分集度，还是在降低中断概率、降低发送功率等方面都显示出CMIMO系统不可比拟的优势，已成为未来无线通信极具发展前景的方向之一。

无线通信中，平均遍历容量是反应用户会话接入性能的重要指标，对系统的网络规划、天线布局等问题的研究具有重要的理论和应用价值。目前已经有一些文献对DMIMO系统平均遍历容量进行了研究。文献[1]以小区平均遍历容量为研究对象分析系统的性能，该文献不足之处在于，只考虑移动台与基站之间的路径损耗对天线的影响，而且信道模型比较简单不具有通用性。文献[2]和[3]给出移动台在小区内均匀分布模型，然而，对于实际的场景（如城市地区），移动台会聚集到某一热点区域且服从非均匀分布。所以，移动台均匀分布的情形并不适用于实际的系统。

因此，在前人研究的基础上本文综合考虑：假设DMIMO系统圆形小区中基站和移动台拥有多根收发天线，信道模型采用综合了快衰落、阴影衰落和路径损耗的复合衰落信道；通过对分布式天线采用覆盖式（BT）传输策略，推导出给定移动台位置时，小区上、下行点对点遍历容量表达式。最后，考虑移动台在小区内任意分布特点，进一步推导出小区平均遍历容量近似闭合表达式。

1 系统模型

如图1所示，考虑一个半径为R圆形小区DMIMO系统，小区内有N个基站，中心基 站记为BS或AP1，其余(N-1)个基站放置在其它位置，每个APn有L根收发天线,移动台（MS）有M根收发天线。不失一般性，分别用(ρ ,θ )，(rn,αn) (n=1,2…，N) 表示移动台和基站在小区内的位置。为方便描述，将上述圆形小区DMIMO系统记为（M,N,L）DMIMO。

基于上述建立的系统模型，假设信道链路是平坦衰落且为准静态的，考虑DMIMO系统的上行链路接收信号的表达式为

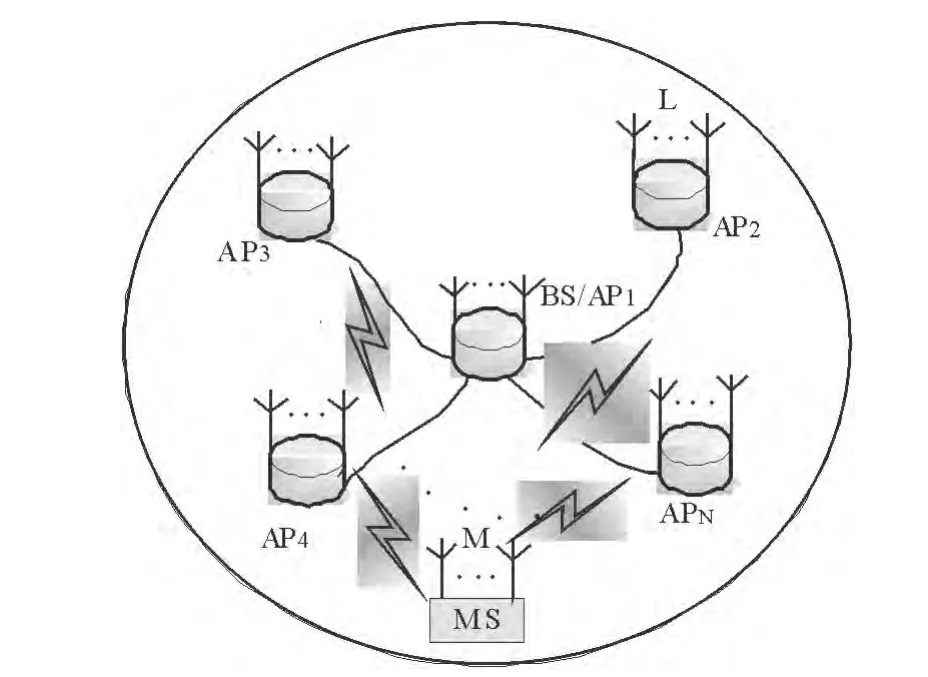
图1 圆形小区DMIMO系统示意图Fig. 1 DMIMO system schematic diagram in a circular area

式中r=[r1,…,rNL]T表示各基站天线的接收信号，x是功率为E(xHx)≤P的发送信号向量，n是具有协方差矩阵E(nnH)=INL的零均值复高斯白噪声向量；信道矩阵为H=[H1…HN]M×NL，其子信道Hn是MS与APn之间的L×M维复合衰落信道矩阵，可以表示为

式中Hw,n是L×M矩阵，表示APn和MS之间的小尺度衰落，且Hw,n中每个元素是零均值单位方差相互独立的复高斯随机变量；hsh,n为APn和MS之间的大尺度衰落，可有如下建模

其中，α是路径损耗指数，c是一个常数，sn代表阴影效应，且服从零均值的对数正态分布，即10log10sn～(0,σsh2)；dn是APn与MS之间的距离。其表达式为：

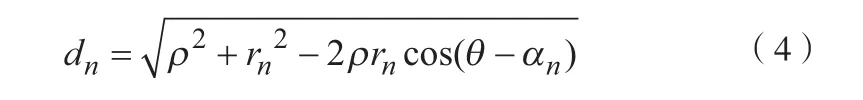
2 小区系统容量分析

本节首先推导分布式天线在覆盖式传输（BT）策略下，MS与APn之间上、下行链路点对点遍历信道容量C(ρ,θ)。由于MS与APn拥有多根收发天线，本文只考虑MS天线数目不超过APn天线数目这种情况，即M≤L；通过给出MS在小区内任意分布模型,推导出小区平均遍历信道容量近似闭合表达式。

2.1 上行点对点链路遍历信道容量

根据第2节中的系统建模，假设接收端已知信道状态信息，发送端未知信道状态信息，可得到上行链路点对点遍历信道容量表达式为

当 M≤L时，上式可转化为

根据Minkowski 不等式[4]，得到容量下界

其中，Wn是具有相同期望和方差的独立随机变量，当N趋向于无穷时,由大数定理有

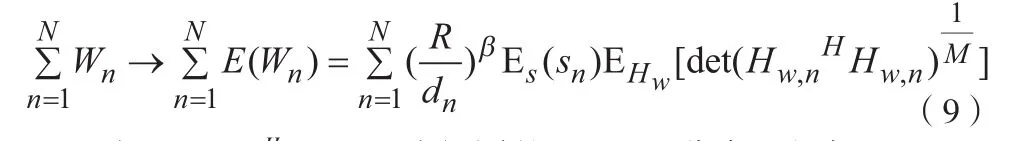
由于(Hw,nHHw,n)服从相同的Wishart分布，根据Wishart矩阵的分布性质[5]，可得到

综合以上推导可得出上行点对点链路遍历容量的近似表达式为

2.2 下行点对点链路遍历信道容量

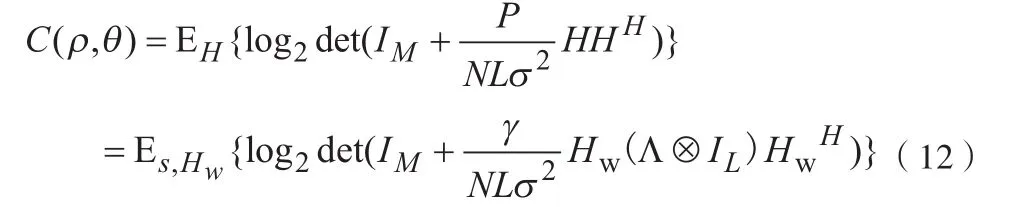
当M≤L时，上式可转化为

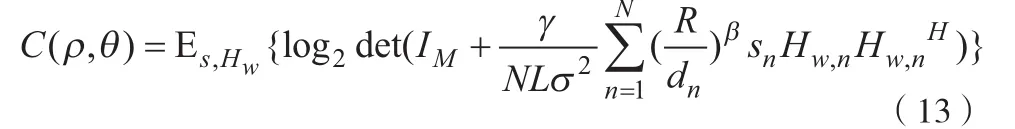
与上行点对点链路遍历容量的推导过程类似，可得出下行点对点链路遍历容量的近似表达式：

3.3 小区平均遍历信道容量

为了体现MS在半径为R的圆形小区分布特点，本文给出MS在小区内的分布模型。如图2所示，将小区分为图中的两个区域，区域1即ψ1是中心坐标为(0,0)半径为r的圆；其余部分为区域2记为ψ2。假设MS在小区内分布的概率密度表达式为

其中，S是整个小区的面积，S1是区域1的面积。λ∈[0,1]表示MS分布在区域1的概率。λ的取值决定MS在小区的分布情况，当λ＜S1/S时，MS集中分布在区域1；当λ＜S1/S 时，MS集中在区域2；当λ＜S1/S时，MS服从均匀分布。特别地，当λ=1时，MS全部集中在区域1，相应的当λ=0时，MS分布在区域2。

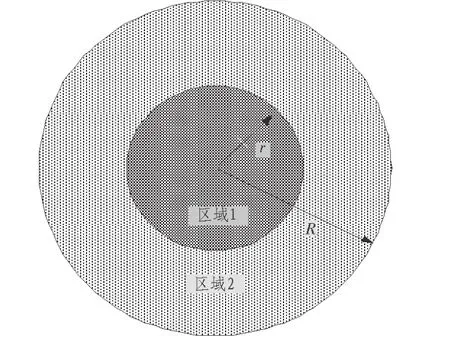
图2 MS在圆形小区内分布模型Fig. 2 MS distribution model in a circular area

考虑MS在小区内的分布情况后,可得出MS在任意分布下，小区平均遍历容量表达式：

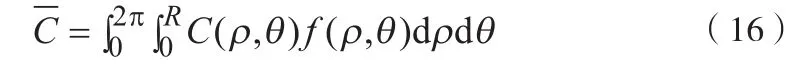
由于MS在小区内是任意分布的，上式一般比较复杂通常无闭合解。本文利用复化Simpson积分公式对小区平均遍历容量进行近似[6]。

3 仿真结果分析

本节通过具体的仿真结果，首先验证所推导的分布式MIMO系统小区上、下行点对点遍历容量理论表达式的准确性。然后，在移动台均匀与非均匀分布条件下，验证小区平均遍历容量理论表达式是否能够反映系统的实际性能。具体仿真参数如表1所示。

表1 系统主要仿真参数Tab.1 Main simulation parameters

图3 DMIMO系统点对点链路的遍历信道容量Fig. 3 Point-to-point link DMIMO system channel capacity

图3给出DMIMO点对点链路遍历信道容量的Monte-Carlo仿真值和理论近似值，图中分别给出上行（3,6,5）DMIMO、下行（3,5,4）DMIMO、下行(2,4,3)DMIMO和上行（1,5,1）DMIMO的性能曲线，从图中不难发现，仿真值与理论值之间的差异较小，充分验证了上述所推导表达式的正确性。

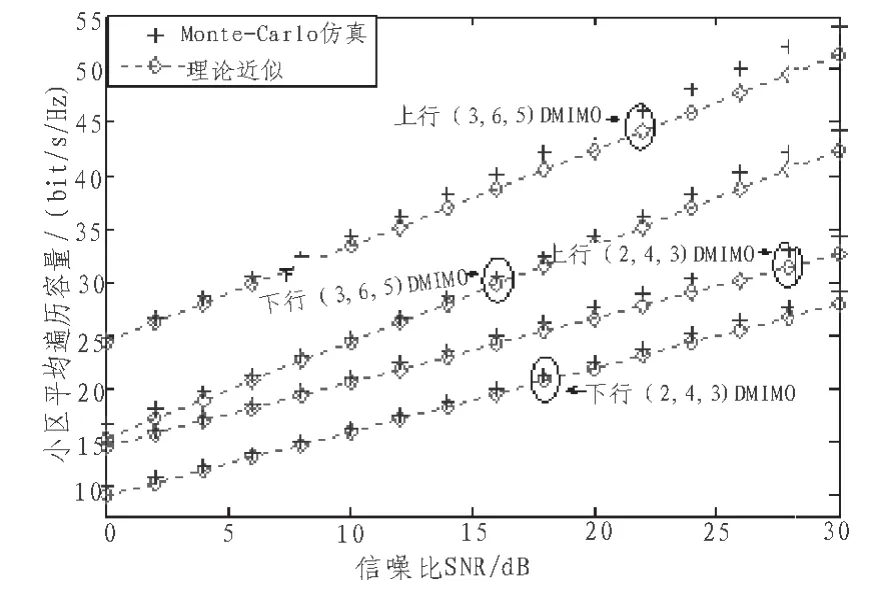
图4 λ=0.25移动台均匀分布小区平均遍历容量Fig. 4 λ=0.25 the average ergodic capacity when mobile station is uniformly distribution

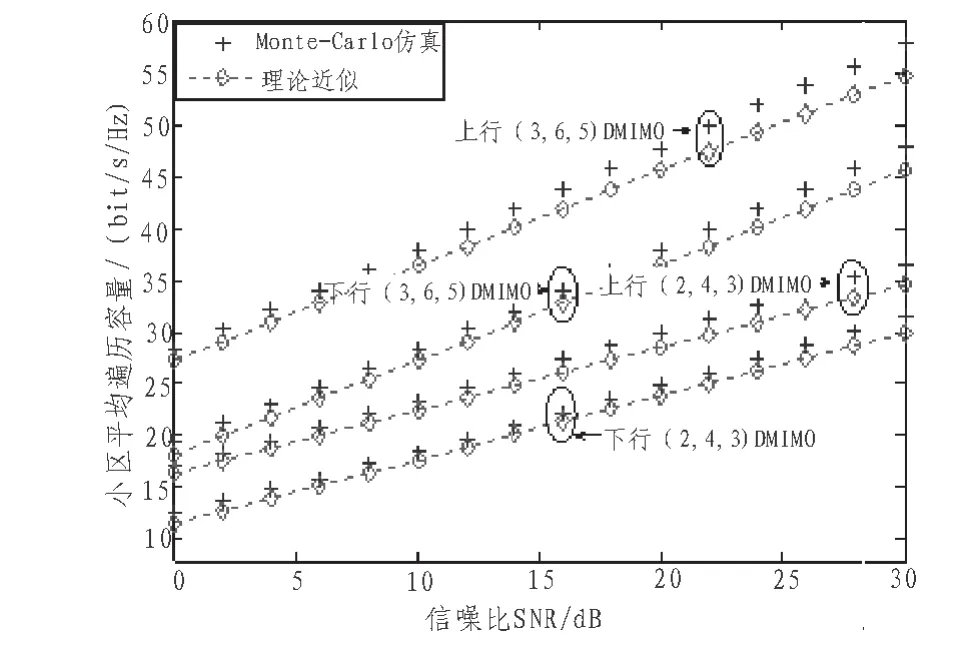
图5 λ=0.4移动台非均匀分布小区平均遍历容量Fig. 5 λ=0.4 the average ergodic capacity when mobile station is arbitrary distribution

图4、图5分别给出移动台均匀分布（λ=0.25）与非均匀分布（λ=0.4）时，（3,6,5）DMIMO、（2,4,3）DMIMO系统上、下行链路性能曲线。通过Monte-Carlo仿真，对 情况下推导的小区平均遍历容量进行验证。比较两幅图可发现，λ=0.4所对应 DMIMO系统小区平均容量要大于λ=0.25所对应的系统容量，当 λ=0.4时，移动台较密集分布于基站周围，它们之间的接入距离减小，相应的路径损耗也随之变小。由此，可得出移动台与基站之间的路径损耗对小区平均遍历容量的影响较大。从图中可看出理论近似值总是很好地逼近仿真值，因此，可以证明推导的近似表达式可很好地反应系统的实际性能，并且可广泛用于分析各种场景下系统容量的评估。

4 结 论

文中研究了分布式MIMO系统在复合信道下的小区平均遍历容量问题。假设移动台与基站有多根收发天线，在发送端采用了覆盖式的传输方式。文章首先推导了给定移动台位置情形下的上、下行链路遍历容量表达式；然后考虑移动台在小区内任意分布特点，进一步推导出小区平均遍历容量的近似闭合表达式。仿真结果显示该表达式的理论值与计算机仿真值很吻合，表明该表达式可以广泛用于各种场景下系统容量的评估，可为未来小区规划、天线布局等问题提供参考。

[1] Wang X ,Zhu P,Chen M.Antenna location design for generalized distributed antenna system[J].IEEE Communications Letter, 2009,5(13):315-317.

[2] Feng W,Li Y-Z, & Gan J-S.On the deployment of antenna elements in generalized multi-user distributed antenna systems[J].Mobile Networks and Applications,2011,16(1):35-45.

[3]Wang X-Z,Zhu P-C,M Chen.Antenna location design for generalized distributed antenna systems[J].IEEE Communications Letters,2009,13(5):315-317.

[4] R A Horn,C R Johnson.Matrix Analysis[M].New York:Cambridge Press,1985.

[5] Antonia M Tulino,Sergio Verd Random. Matrix Theory and Wireless Communications[M].Boston:Now Publishers Inc,2004.

[6] R L Burden,J D Faires.Numerical Edition[M]. Analysis Fourth Boston:PWS-KENT,1994.

The average ergodic capacity analysis for distributed MIMO antenna systems

CUI Lei, CAI Jun
（Hohai University,Nanjing 211100, China）

The article will study the average ergodic capacity for distributed MIMO antenna systems in a circular area.Firstly, we’ll establishe a composite channel model which includes fast fading,shadow fading and path loss. Then,distributed antenna cover transmission strategy is emploied, by giving the mobile station’s location, we deduce the point-to-point uplink and downlink ergodic capacity theory expression at high SNR. Finally, considering the mobile station arbitrary distribution characteristics in the neighborhood, we further deduce the average ergodic capacity closed approximate expression. The simulation results show that the theoretical expression can accurately react the actual system performance.

distributed MIMO antenna systems; composite channel; average ergodic capacity; arbitrary distribution

TN911.2

A

1674-6236(2014)03-0069-04

2013–06–05 稿件编号：201306028

崔 磊(1987—)，男，江苏淮安人，硕士研究生。研究方向：信号与信息处理。