基于改进的BP神经网络空空导弹攻击区解算方法

王海涛，佟惠军，王 洋

（空军航空大学 作战指挥系，吉林 长春 130022）

基于改进的BP神经网络空空导弹攻击区解算方法

王海涛，佟惠军，王 洋

（空军航空大学 作战指挥系，吉林 长春 130022）

针对目前空空导弹可攻击区解算精度不高、收敛速度较慢的问题，提出了一种基于BP神经网络的改进的空空导弹攻击区解算方法。引入动量项的算法加快收敛的速度，并采用对灵敏变量插值的方法提高拟合精度，仿真结果表明：该方法具有精度高、参数少、通用性强的优点。

BP神经网络；空空导弹；动量项；插值

空空导弹攻击区是指：当载机在此区域发射导弹时，导弹就能以一定的概率杀伤目标[1]。空空导弹攻击区解算精度的高低、解算速度的快慢直接关系到空战的成功与否。现有的空空导弹攻击区解算方法主要有：一般拟合法、三角变换拟合法、插值法。这些方法一般很难同时满足拟合精度与收敛速度的要求，且通用性较差，不能适应未来空战复杂多变的战场环境。

文中采用基于改进的BP神经网络的方法，通过网络结构参数的合理选择，反复进行训练，对攻击区参数与战术诸元进行非线性关系的拟合。通过离线训练来获得网络模型参数，并通过网络模型在线计算进而得到实时的、高精度的空空导弹的攻击区计算结果。仿真结果表明，该方法可有效提高导弹攻击区解算精度和收敛速度，且通用性较好，为后续火控系统的改进提供了便利。

1 空空导弹攻击区的数学描述和准确度计算

1.1 空空导弹攻击区的数学描述

空空导弹的真实攻击区需要通过大量的实战统计获得，但这又是不可能的，本文采用空空导弹仿真获得的攻击区来代替真实攻击区[2]。空空导弹攻击区的大小和形状，受导弹性能、载机飞行高度、速度、离轴角、进入角，目标速度、目标高度差、机动能力、方位角、攻击航向相对太阳夹角、气象条件等诸多因素的影响，随着发射条件的变化而变化。一般来说，导弹的远边界Rmax和近边界Rmin是高度、速度、机动过载、离轴角、进入角等初始攻击条件的非线性函数，即

式中hA，hT分别为攻击机高度和目标高度，vA，vT是攻击机及目标的速度，nT是目标机动过载，q和qT分别是导弹离轴角和目标进入角。

1.2 攻击区准确程度的概率计算

将由导弹六自由度运动方程计算得到的导弹发射区称为理论攻击区[3]，将火力控制系统中使用的经拟合或快速模拟等方法得到的导弹攻击区称为实际攻击区，总的要求是实际攻击区应该完全重合于理论攻击区，但是实际上是做不到的，因为在建立实际攻击区的计算中，进行了一些必要的简化，这就导致了两者的不重合，对它们之间重合度用发射成功概率表示。图1表示了在一定条件下的导弹理论攻击区和实际攻击区的关系[4]。

图中实际攻击区是火控系统中用以判断是否到达发射条件的依据，而理论攻击区是火力控制中无法实现的模型，要求两者重合，特别是在全部飞行包线范围内重合是不可能的，在图中取两个攻击区重合部分面积Ac，在此范围发射导弹是可行的。

图1 失去发射机会概率和界外误发射概率Fig. 1 Loss of emission chance probability and outside emission probability

图1中左边理论攻击区拥有的部分面积AM，攻击机在此区域发射导弹是完全可行的，但机载火力控制系统不能准确反映此面积的存在，即攻击机在此区域会失去发射导弹的机会；图中实际攻击区拥有但已经在理论攻击区之外的部分面积Af，攻击机在此区域是不能发射导弹的，但机载火力控制系统却允许发射导弹，造成无效的界外发射。因此，在实际攻击区解算中，应尽量使实际攻击区与理论攻击区重合，并将失去发射机会和误发射机会降至最低。

在评价实际攻击区的精度时，通常以两个概率值表示，即失去发射机会的概率：

界外发射机会的概率：

机载火控系统中所使用实际攻击区优劣的数量指标即可使用这两个指标进行评价。为得到较高的发射成功概率Psl，必须将这两个概率控制在15%以内，即

考虑到失去发射机会和界外发射机会的概率均为小概率事件，故可令

由于各传感器存在的系统误差和随机误差都会影响到攻击区的边界大小，因此必须使界外发射机会和失去发射机会的概率均要小于15%以此来保证发射成功概率大于70%，在评估和验算时，必须将系统误差和随机误差都考虑进去。

2 BP神经网络模型分析

2.1 一般BP网络模型

应用BP神经网络的方法可以求解一些存在大量范例的非结构性问题，导弹攻击区处理的特点与非结构问题有很大的相似。BP神经网络所需要的大量范例和样本可由空空导弹理论攻击区来提供[5]。

BP神经网络是一种被广泛采用的人工神经网络模型。它是一种多层反馈的神经网络，网络的各层之间的权值修正是在误差反向传播的过程中完成的。BP神经网络计算空空导弹攻击区参数的基本思路：

对BP前馈神经网络用足够多的已有样本来进行训练，通过训练比较网络实际输出和期望之间的差值来不断调节网络权值，直至输出层的误差满足精度要求时停止训练。

采用三层BP网络来逼近导弹的攻击区，将影响空空导弹攻击区的 hA、hT、vA、vT、q、qT作为本网络的输入，攻击区的远边界Rmax和近边界Rmin作为网络的输出。

本文选用确定隐层神经元数的公式为：

式中，[x]表示取不大于x的最大整数；n和k分别表示输入和输出神经元个数。本文输入神经元个数为6，输出神经元个数为2，隐含层节点数为5。

根据非线性系统处理的一般经验，初始权值不宜选取太大，也不宜太小。一般初始权值的随机数取值范围是（-1 ,1）。采用计算机模拟仿真的结果作为导弹攻击区的样本集，并对数据进行归一化处理。

2.2 改进的BP神经网络模型

根据空战经验发现，目标进入角qT是对攻击区形状影响最明显的变量。如果采用上述BP神经网络进行攻击区的拟合，不仅难度大，而且精度较差，可以采用不同的qT分别拟合Rmax、Rmin，并将插值法运用到攻击区的求解中。在BP的学习过程中，学习步长η的选择很重要，η值大会导致权值变化增大，BP的学习收敛效率更高，但η值过大就会引起震荡网络的不稳定，收敛速度随之变慢。为此，对BP神经网络加入“动量项”[6]。

本方法仍采用三层BP网络的拟合方法关系，隐层神经元数取为m=5。在获得不同的RqT,max，RqT,min后，对其进行插值即可获得空空导弹攻击区。改进算法的权值调整为：

Δwij(n)为第n次迭代时I层与J层之间的权值修正向量，η为对应w的学习步长，δj(n)为第n次迭代时第J层第j个神经元的局部梯度，v为第n次迭代时第i个神经元的输出。其中ηij对步长进行适当调节，α取(0,1)的常数，α作为动量项，且一般为正数，完成对上一时刻权值修正方向的记忆，提高学习效率。通过对某型空空导弹的理论攻击区的研究发现，在攻击条件的主要因素中，目标进入角对导弹攻击区的影响最大，且难以进行定量或定性关系式的描述。

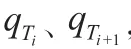
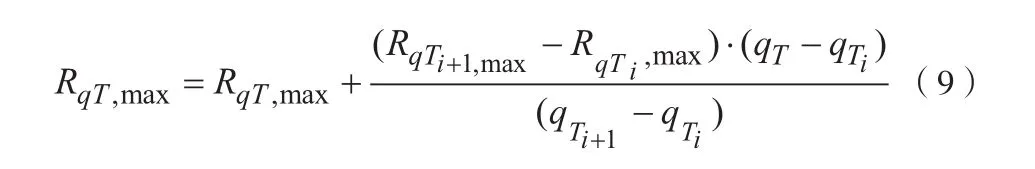
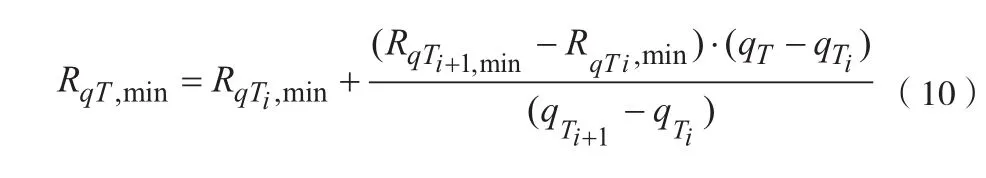
3 BP网络模型仿真结果分析

选择某型空空导弹的300个典型的理论攻击区进行仿真分析，利用一般的拟合法、插值法、三角变换拟合法及本文的基于改进的BP网络的解算方法进行拟合，选取300个具有代表性的攻击条件，代入相应的拟合关系式进行计算，并将拟合结果与理论的攻击区进行比较[7]。图2 给出了当 hA=hT=3 000 m, vT=400 m/s, ny=0, q=0时4种攻击区比较。

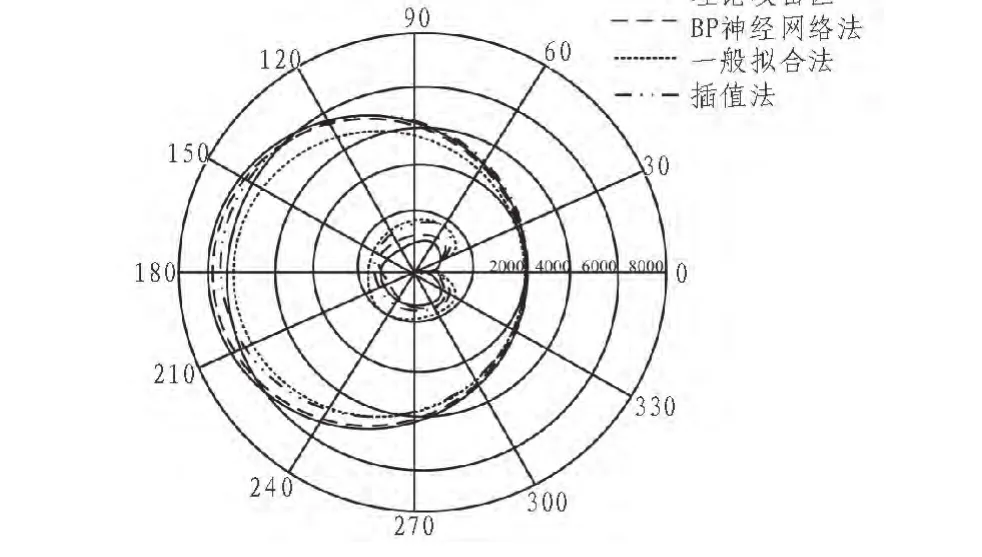
图2 目标不机动时4种攻击区比较Fig. 2 Comparison of four kinds of attack area about non-unmaneuvering target

求出相应的失去发射机会的概率Pmt和界外发射机会的概率Pab，最终得出如表1所示的仿真结果。

表1 不同解算方法的精度对比Tab.1 Comparison of precision about different calculating methods

由仿真结果可知，改进的BP神经网络方法的拟合结果与理论的攻击区基本重合，它的逼近精度仅比插值法低少许，比三角变换拟合法，特别是比一般的拟合方法有很大幅度的提高。为更好的帮助研究者进行方法的选择，对这4种方法在拟合系数的多少、拟合精度及通用性等方面上的优缺点进行更直观比较，得出结果如表2所示。

从表2可以看出，从拟合精度、拟合系数、解算的方便程度、方法的通用性等方面进行综合权衡，本文提出的改进的BP神经网络方法是最好的。改进的BP神经网络算法主要做了两方面的改进，一方面是采用动量项的算法，加快了收敛的速度，同时也可避免学习过程陷入局部最小的误区；另一方面吸取了插值法的优点，提高了拟合精度。

表2 4种解算方法的特点比较Tab.2 Comparison of characteristics about the four kinds of calculating methods

4 结束语

文中提出的用于近距格斗空空导弹[9]攻击区改进的BP神经网络方法，不仅具有很高的拟合精度，而且通用性好、存储量小，完全可以满足当前的机载火控计算机在计算速度、拟合精度上和存储量方面的苛刻要求，具有很广阔的应用前景。从分析结果可知，插值法在拟合精度、解算方便程度等方面也可以满足实战要求，因此实战中可根据机载火控系统配置和对作战精度的要求决定采用插值法或改进的BP神经网络算法。

[1] 王凯,李望西,轩永波.基于BP神经网络的空空导弹攻击区解算及其仿真[J].弹箭与制导学报,2010,2(1):75-77.

WANG Kai, LI Wang-xi, XUAN Yong-bo. The solution and simulation of air-to-air missile launch envelopes based on BP neural network[J]. Journal of Projectiles, Rockets, Missiles and Guidance,2010,2(1):75-77.

[2] 王宏伦,吕庆风,董胜龙,等.基于模糊逻辑系统的空空导弹攻击区拟合[J].南京航空航天大学报,2000,6(3):305-310.

WANG Hong-lun, LV Qing-feng, DONG Sheng-long,et al Missile launch envelope approximation based on fuzzy logic system[J]. Journal of Nanjing University of Aeronautics& Astronautics,2000,6(3):305-310.

[3] 付书堂,章惠君.空空导弹攻击区高精度快速计算方法[J].科学技术与工程,2012,9(12):7074-7077.

FU Shu-tang, ZHANG Hui-jun. A method of high-precision and fast calculation for attack area of air-to-air missile[J].Science Technology and Engineering,2012,9(12):7074-7077.

[4] 周志刚.机载火力控制系统分析[M].北京:国防工业出版社,2008

[5] 张列航,雷蕾,李研生.BP神经网络导弹攻击区火控工作式拟合[J].火力与指挥控制,2011,12(12):177-179.

ZHANG Lie-hang, LEI Lei, LI Yans-heng. Fire ontrol c formula fitting of missile attack envelop based on BP neural network[J].Fire Control & Command Control,2011,12(12):177-179.

[6] 查立宏,章代雨,李胜林.基于BP神经网络的空空导弹攻击区精确拟合[J].制导与引信,2005,12(4):20-24.

ZHA Li-hong, ZHANG Dai-yu, LI Sheng-lin. Accuracy fitting of air-to-air missile impact area based on BP neural network[J].Guidance & Fuze,2005,12(4):20-24.

[7] 张平,方洋旺,金冲.空空导弹攻击区实时解算的新方法[J].弹道学报,2010,12(4):11-15.

ZHANG Ping, FANG Yang-wang, JIN Chong. A new method of real-time calculation for attack area of air to air missile[J]. Journal of Ballistics,2010,12(4):20-24.

[8] 易华,谢希权.基于自适应模糊系统的多目标导弹攻击区解算[J].系统工程与电子技术,2002,2(1):45-48.

YI Hua, XIE Xi-quan. Algorithm for the missile launching envelop in multi-target attacking based on the adaptive fuzzy system[J].System Engineering and Electronics,2002,2(1):45-48.

[9] 张世欣,韩应都.空空导弹仿真系统的设计[J].电子科技,2012(7):80-82.

ZHANG Shi-xin,HAN Ying-du. The design of the air-to-air missile simulation system[J].Electronic Science and Technology,2012(7):80-82.

The solution of air-to-air missile launch envelopes based on the improved BP neural network

WANG Hai-tao, TONG Hui-jun, WANG Yang
（ Department of Combat and Command, The Aviation University of Air Force, Changchun 130022,China）

In order to solve the problem of the low accuracy and convergence speed of air-to-air missile launch envelopes, the article has presented a solution of air-to-air missile launch envelopes based on the improved BP neural network. Introduce the momentum item to accelerate the convergence speed, and using interpolation methods on sensitive variable to improve the fitting accuracy. Simulation results show that the method has advantages of high accuracy, less parameters, versatility.

BP neural network; air-to-air missile; the momentum item; interpolation

TN702

A

1674-6236(2014)03-0028-03

2013–06–16 稿件编号：201306099

王海涛(1990—)，男，山东聊城人，硕士研究生。研究方向：制导武器的作战使用与仿真。