嵌入式精密三角高程测量算法设计与实现

杨雪

(广东省公路勘察规划设计院股份有限公司，广东广州 510507)

1 引言

几何水准测量具有测量精度高、方法简便等特点，一直是高程测量的主要方法。但其:视线短、速度慢、劳动强度大，仅适用于平坦地区。因此许多学者都对高度角观测和大气折光的影响进行了深入研究，通过提高三角高程测量的精度，在一定的精度范围内，代替几何水准测量。

EDM三角高程测量研究已取得很大的进展。EDM三角高程测量通过观测水平距离和天顶距求定两点间高差，且顾及地球弯曲和大气垂直折光影响。研究表明，三角高程测量可以代替四等水准测量，甚至达到二等水准测量要求［1］。

2 技术原理

2.1 EDM精密三角高程测量基本原理

精密三角高程测量观测原理如图1所示［2］:

图1 精密三角高程测量原理图

在1位置上的全站仪对A点棱镜观测斜距和竖直角，则可计算A点到1位置上全站仪中心的高差:

在1、2位置上的全站仪进行对向观测，两仪器中心间的高差为:

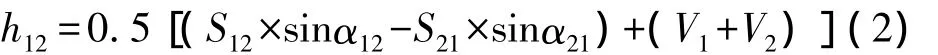
将1位置上的全站仪迁至3位置，2～3为对向观测边，两仪器中心间的高差为:

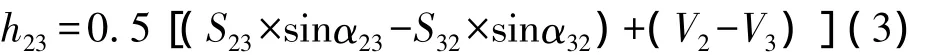
在N位置上的全站仪对B点棱镜观测斜距和竖直角，则可计算3位置上全站仪中心到水准点B的高差［2］:

在实际应用中，为提高测量精度，采用两台自动照准的高精度全站仪，并将照准棱镜固定在全站仪的把手上(如图4所示)，进行同时对向观测，可基本消除大气垂直折光的影响。设计测段对向观测为偶数边，测段起末固定棱镜杆，可消除仪器高和觇标高影响。最后限制观测边的长度和高度角，可减少相对垂线偏差的影响［3］。

2.2 嵌入式开发环境与设备

Windows CE是微软公司嵌入式、移动计算平台的基础，它是一个开放的、可升级的32位嵌入式操作系统，是基于掌上型电脑类的电子设备操作系统［4］。野外实时电子记录要求载体小巧轻便，便于携带，载体功能和可扩展性强，能够满足测绘作业记录与实时测算等多方面要求。选择WinCE系统是由于目前很多载体如掌上电脑、GPS测量手簿、智能手机等移动设备都应用WinCE系统。本文介绍的精密三角高程测量记录与测算应用程序不仅可以应用于掌上电脑，所有WinCE系统平台或者是Windows系统平台的操作系统均可以安装并使用。

3 功能设计和算法实现

程序运用C#编程语言，开发平台为Microsoft Visual Studio 2005(简称VS2005)，运用VS2005的设备模拟器对编写的程序进行PDA(掌上电脑)上的调试。精密三角高程测量程序界面布置及功能如图2所示:

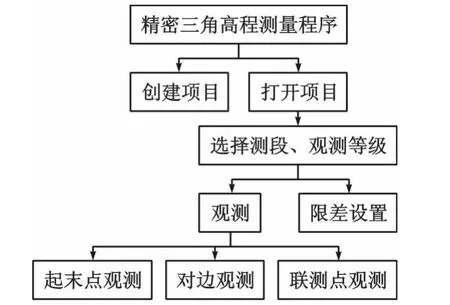
图2 精密三角高程测量程序功能布置图

每条测边需要测量一次平距用于计算本测段限差与需要满足限差要求的测回数目。每半测回分别观测记录对面高低棱镜的斜距、天顶距、高差，一个测回结束后“保存”，重复观测几个测回后进行“重新通过”计算。重新通过用于计算各项指标是否超限。以下介绍了二等、三等观测的限差要求:

二等观测限差:各测回垂直角和指标差不超过5″，距离不超过 3 mm。测段往返测高差不符值不超出，双棱镜观测时按高低棱镜观测值分别计算高差，不符值不超出，并在测站上要检核高低棱镜观测高差之差。

三等观测限差:各测回垂直角和指标差不超过6″，距离不超过 5 mm。双棱镜观测时按高低棱镜观测值分别计算高差，不符值不超出为测量线路长，单位km)，并在测站上要检核高低棱镜观测高差之差。

观测数据的解算流程图如图3所示:

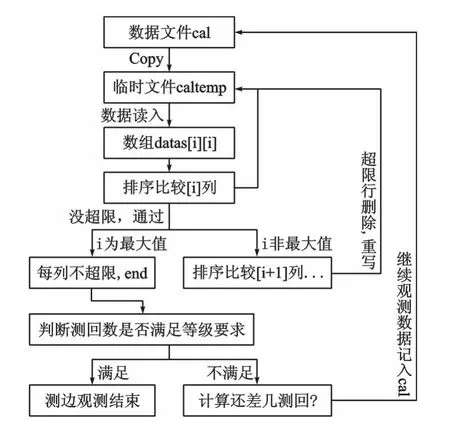
图3 观测数据解算流程图

4 实验基本情况

某市江顺大桥工程项目中心位置在东经113°04'，北纬22°47'，全长约 4 km。

采用徕卡TC702、徕卡TS06(标称精度2″)全站仪。

4.1 高低棱镜的定制

高低棱镜镜头中心之间高差常数的测定。在平地相隔 20 m左右，分别架设全站仪和高低棱镜，全站仪直接设置测定高差。先测定低棱镜高差，读10次取平均值。再测定高棱镜高差，读10次取平均值。将高棱镜高差减去低棱镜高差，即得高、低棱镜常数。本次实验的两组高低棱镜的棱镜高低差分别为 0.117 m和0.113 m。

制作框架要求安装后两个棱镜尽可能垂直，如果不垂直对观测精度的影响较大。

4.2 测量过程

GM 路线:GM18－JS15－JS16－GM18;

JS路线:JS04－JS18－JS17－JS04。

每个测段的起末点观测，要求在测段水准点附近架设全站仪，在水准点上架设棱镜杆(起、末点为同一根杆，长度不变)，进行距离和高度角观测;低棱镜两测回，高棱镜两测回;观测时各站上要在观测前测定温度和气压，以便对边长进行改正。

对向观测时，按仪器前进方向，先进行后测站观测，再进行前测站观测。每个测段进行单棱镜往返测或高低双棱镜观测，高低双棱镜观测顺序为:后低，前低，前高，后高。支线测段进行单棱镜往返测。一条边观测结束后，进行下条边观测，这时特别要注意，前站仪器不动，为下条边的后站，原后仪器迁至前面，为下条边的前站，在一个测段上对向观测的边为偶数条边。对向观测顺序如图4所示:

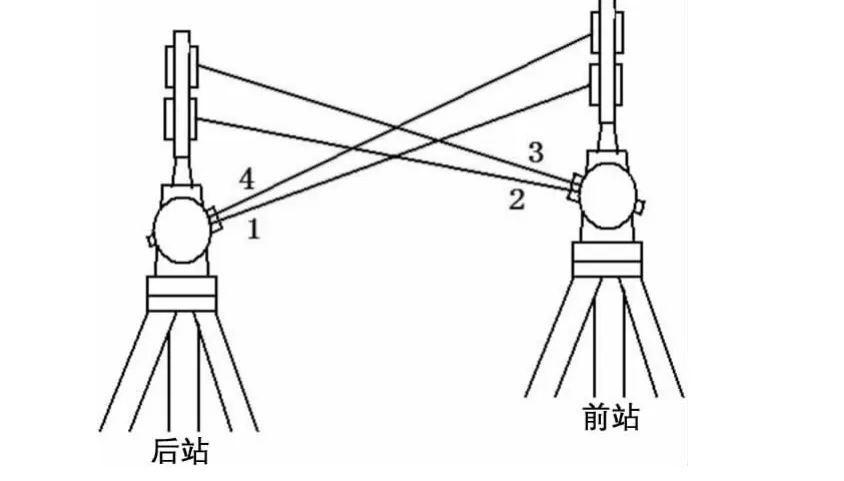
图4 对向观测顺序示意图

4.3 数据精度统计

经过对GM线路和JS线路的记录数据进行解算分别得到表1、表2所示结果，并分别与传统水准测量的成果进行了比较。

GM线路计算成果比较表 表1

JS线路计算成果比较表 表2

以上两表中所示精密三角高程测量高差由高低棱镜分别得到的高差取平均所得。

5 数据分析

表1中JS16－GM18测段是导致GM路线精密三角高程测量闭合差偏大的主因;而导致JS路线精密三角高程测量闭合差偏大的主因是表2中JS17－JS04测段。

对观测数据进行统计分析发现，JS16－GM18、JS17－JS04测段普遍存在三个因素导致数据精度下降。

1）适应证不适宜。实例1：患者男性，35岁；诊断：混合痔；处方用药：阿奇霉素肠溶胶囊0.25 g qd 7 d、化痔栓1.7 g qd 7 d。用药分析：阿奇霉素首选应用于革兰氏阳性菌及支原体、衣原体等非典型病原体的呼吸道感染性疾病，不能覆盖痔疮可能的致病菌肠道杆菌等革兰氏阴性菌，且血药浓度不高，属于抗生素选择不适宜，应改用左氧氟沙星等氟喹诺酮类抗菌药物。

5.1 高、低棱镜常数的检核

测站高低棱镜常数检核反映的是同一测回高低棱镜分别计算的高差差值，理论上该差值应该等于该测站上仪器所观测的对面高低棱镜的高、低棱镜常数，即0.117 m或 0.113 m。该值可以判断出观测质量，对后期高差准确性起重要作用，实验数据显示距离大的测段，由每测回观测数据计算的高低棱镜高差与事先测好的高低棱镜常数偏大均较大。这说明观测质量较差，误差比较大。

根据实际作业情况，认为每观测一组数据经记录后，程序计算的高低棱镜高差值与高低镜事先测定的常数(0.117 m/0.113 m)不超过 3 mm为宜。

高低棱镜常数为0.117 m的高低棱镜组在定制时有些许倾斜，原因是在定制过程中铆钉没有十分垂直，在距离较近的观测中这种误差几乎可以忽略，但是当距离加大时，这种影响就会总使高低棱镜高差检核达不到要求。

5.2 观测距离的影响

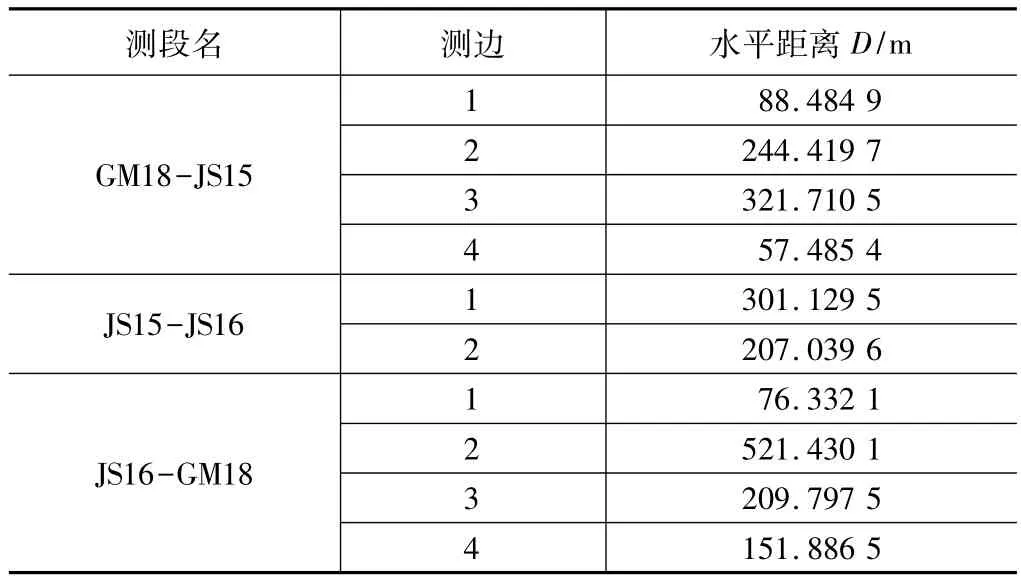
GM路线各测段测边与距离 表3

如表3所示，JS16～GM18这个测段测站最长距离521 m，对于普通全站仪，当距离较大时，棱镜目标模糊而微小，观测员只能靠估读。根据精密三角高程测量原理，智能全站仪在二、三等观测对边观测边长一般在 200 m～500 m，丘陵地区、山地最长为 1000 m。可见该测段的观测距离选择为 521 m，已经超出平地智能全站仪观测限制距离，作业人员选择的观测距离过长，人眼观测误差和仪器精度限制使得GM路线第4测段最终算得高差产生了较大的误差。

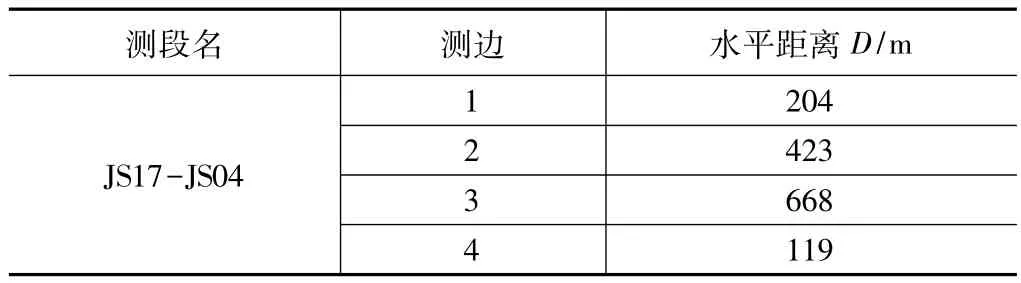
JS路线JS17－JS04测段测边与距离 表4

同理表4所示的JS线路JS17－JS04路段第3个测边达到 668 m，可见距离过长对普通全站仪来讲是导致精度损失的主要因素。

根据实验结果，在平坦地区受距离因素制约，使用精密三角高程测量无法充分体现其优越性，但是在地形起伏变化较大的山区和坡度较大的路段，可以考虑精密三角高程测量代替传统水准测量［5］。

5.3 测回数目的影响

距离越长要求符合条件的测回数相应越要增加，满足要求的测回数不足也是导致JS16－GM18路段误差较大的重要因素。

GM路线JS16－GM18测段测回数 表5

综上，实验表明，保证天气条件良好稳定、保证严格检核高低棱镜常数、保证观测测回数充足，保证观测距离合理，EDM三角高程测量可以满足精密工程测量要求［7］。

6 结语

(1)对于普通全站仪，影响数据精度的首要因素是距离，因为距离长人眼观测大多为估测;仪器本身精度情况也有限制;棱镜与望远镜之间的大气涌动在长距离也表现明显，尤其是日出与日落、大风、气温渐渐升高等天气影响尤为严重。距离大于 600 m时开始观测困难，无效数据增多，数据误差也相应变大。距离较长时为了增加观测的可靠性，可以定做合适的觇标。

(2)观测数据经过解算后满足要求的测回数目要充足。尤其在远距离观测时，满足指标差和垂直角限差的测回数目要足够多，才能保证精度的可靠性。

(3)测站上要严格检核高低棱镜常数。由分析数据可知，观测数据计算的高低棱镜高差与之前测定好的高低棱镜常数(本试验中是 0.117 m与 0.113 m)之间的差值越小越准。建议差异在 3 mm以内，如果超出 3 mm，要重新测量，可以多测一些测回，但是不能少测，否则会影响整体精度，精密三角高程测量如果有一条测边测错，那么整个测段都要重新测过，所以保证每个测站上的观测测回数目，避免重复劳动。棱镜固定框定制的环节要使安装后的两棱镜中心线尽量垂直重合。

(4)在天气条件较差的情况下精密三角高程测量精度和效率同时降低［8］，因此一定要选择天气状况平稳，温度气压适宜的时间段进行精密三角高程测量。

［1］宁津生，陈俊勇，李德仁等.测绘学概论［M］.武汉:武汉大学出版社，2008(5).

［2］潘正风，杨正尧，程效军等.数字测图原理与方法［M］.武汉:武汉大学出版社，2009(9).

［3］杨敏，陈国世.高精度对向三角高程代替等级水准测量的可行性研究［J］.地理空间信息，2011(1):131～132.

［4］Karli Watson，Jacob Vibe Hammer等.C－#入门经典(第六版)［M］.北京:清华大学出版社，2013(6).

［5］昝峰.精密三角高程测量在公路测量中的应用［J］.测绘与空间地理信息，2011(1):186～187.

［6］李凯，石力，朱清海.应用精密三角高程测量替代二等水准测量［J］.城市勘测，2012(5):89～93.

［7］刘冠兰，李东宇，丁文宏.精密三角高程测量在宽水域跨河水准中的应用［J］.工程勘察，2010(10):71～74.

［8］孙良宇，潘国盛，康继波等.浅析一、二等测距三角高程法跨河水准测量的误差来源［J］.测绘与空间地理信息，2012(5):179～182.