基于自适应Kriging代理模型的叶型气动优化设计

余 锐， 周代伟， 竺晓程， 杜朝辉

（1.上海交通大学 航空航天学院，上海200240；

2.上海电气电站设备有限公司上海汽轮机厂，上海200240）

叶型的气动设计是现代叶轮机械设计的核心技术.合理高效的叶型是提高叶轮机械性能、降低叶轮机械运行成本的前提条件之一.叶型的优化设计往往要求在满足各种性能结构约束的前提下改善叶型的气动参数.目前叶型的气动外形设计有反设计和优化设计2种方法.反设计需要给出目标压力分布或表面速度分布，将目标压力分布转化为叶型几何外形是一个比较困难且对经验有较高要求的问题.随着优化算法的发展和计算机水平的提高，基于随机性寻优的优化设计方法被广泛使用.虽然随机性优化算法具有良好的全局性、鲁棒性及高并行性等特点，但多维大寻优空间导致收敛速度慢是制约该算法应用的主要障碍.建立高效的目标评价方法、合理设计优化参数空间和提高优化算法的寻优效率是应用随机性优化算法的重要前提.虽然目前大多数透平型线已具有较高的热力效率，但是作为组成叶片基本单元的型线，对其进行优化设计仍是目前进行三维叶片设计的必要步骤.

基于梯度的优化算法最早被运用于叶片的气动数值优化设计中.Burguburu［1］采用基于梯度的优化算法耦合N－S求解器对3种叶轮机械叶片进行了优化设计，提高了叶片的效率.然而由于基于梯度的优化算法易陷入局部最优，且难以适应叶片气动优化设计多模态的特点，因而一些具有较好全局寻优能力的启发式算法逐渐广泛应用于优化设计中［2］.Oyama［3］采用遗传算法对 NASA Rotor67压气机叶片进行优化设计，取得了较好的效果.ÖKSÜZ［4］介绍了一种用于三维燃气轮机叶片的气动优化设计，采用遗传算法分别对叶片的气动效率和扭矩进行单目标优化，结果表明，优化后叶片的气动效率从83.9%提高到85.9%，扭矩增大了7.6%，完成了对原型叶片的改进.全局寻优的算法需要大量CFD计算，时间耗费巨大，不能满足实际的气动设计和工程应用.在设计变量与优化目标间构造近似模型（又称代理模型）来替代CFD计算进行寻优可以很好地解决上述问题，因此，该方法得到了越来越多的应用［5］.薛亮等［6］采用二次多项式近似模型及改进遗传算法，省时高效地完成了对NASA Rotor67动叶片叶型的优化设计，使得叶片绝热效率提高了1.1%.高行山等［7］在涡轮叶片气动优化时引入近似技术，加速了整个寻优过程，通过对某涡轮叶片的优化分析验证了该方法的可行性.Mengistu等［8］采用遗传算法构造优化目标与优化变量间的近似模型，以最大化绝热效率、压比和最小化总压损失为优化目标，对亚音速涡轮叶栅二维流动情况进行优化改进.最后通过4组方案分析了设计参数对叶片气动性能的影响，得到了更优的叶型.王红涛［9］对比分析了基于自适应Kriging代理模型的优化算法与小生境微种群遗传算法，发现基于自适应Kriging代理模型的引入减少了迭代所需调用CFD计算的次数，有效地提高了优化过程的效率.

笔者采用基于自适应Kriging代理模型的近似代理技术建立具有全局寻优能力的优化算法，通过对叶型进行参数化描述，代入RANS方程求解得到叶型气动性能参数，建立叶型气动优化设计方法，并以压力恢复系数为目标函数，使用该方法对某设计工况下的叶型进行了优化设计，验证了整个优化系统的可靠性，提高了叶型的性能.

1 数值优化方法

一般对于带有约束条件的优化问题可采用如下表达形式

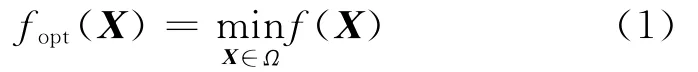
式中：X为设计变量；fopt（X）为目标函数的最优值；X＝［x1，x2，…，xn］T，代表在n维空间Rn中的点，即优化问题中的1组方案；Ω为设计变量的定义域；gi（X）和hj（X）为约束函数.

式（2）中的优化问题需要满足2种约束条件：不等式约束和等式约束.按照规范化形式，一般都将优化问题归结为目标函数的于极小值问题，对于目标函数极大化问题可以通过转换为对应的极小化问题求解.

图1给出了基于自适应Kriging代理模型的叶型气动优化设计流程示意图.由图1可知，该系统以调节叶型形状的控制参数作为设计变量，通过试验设计（DOE）获得初始的设计变量样本集.并在完成对叶型网格的自动生成和流场的求解分析后，获取目标函数信息（即响应样本集）.进而采用自适应Kriging代理模型构造变量和响应间的近似模型，完成校正点的寻找和评估.若不收敛，将校正点和对应响应值加入样本库，不断更新代理模型直至收敛，获得目标函数最优的叶型.该系统将试验设计、CFD数值模拟和优化设计方法相结合，自动完成各模块间的数据传递，减少了人工干预且极大地提高了叶型开发效率.

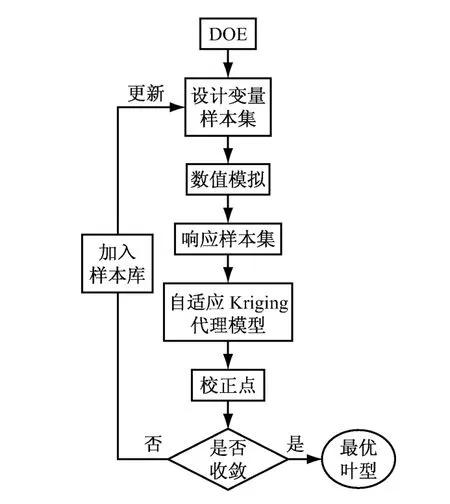
图1 基于自适应Kriging代理模型的叶型气动优化设计流程Fig.1 Flowchart of airfoil aerodynamic optimization design based on adaptive Kriging surrogate model

1.1 优化算法

全局优化算法（如遗传算法等）虽然可以使优化问题避免陷入局部最优，但由于耗时巨大，难以直接应用于实际工程优化设计中.因而采用代理模型代替数值模拟手段是一种行之有效的方法，可以大大减少优化过程的计算量、提高优化效率及优化算法的性能和组成更好的优化策略.

常用的代理模型主要有多项式响应面模型、径向基函数模型和Kriging模型等.笔者对叶型优化时选取的算法是一种基于自适应Kriging代理模型的自适应序贯优化算法［10］.由于Kriging模型在训练样本点处满足无偏估计，具有良好的高度非线性近似能力，因此最适合在叶型优化等高度非线性优化问题中作为代理模型使用.

Kriging模型假设样本点x（维数为m）与对应响应值y之间的关系为

式中：f（）x为确定性部分，可以用一个常数表示，是对设计空间的全局近似；z（x）为一随机过程，表示对全局近似的背离.

该随机过程与全局模型的局部偏差是由相关函数反映的.z（x）具有期望为0，方差为σ2的统计特征.方差σ2反映了试验的精度，一般σ2越大，表示试验误差越大.随机过程z（x）的协方差为：

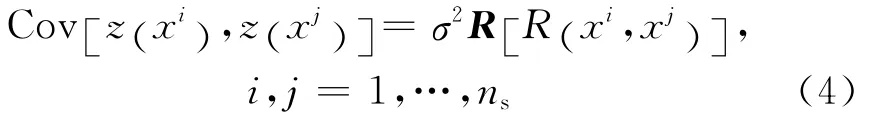
式中：R为相关函数矩阵；ns为样本点个数；R （xi，xj）为点（xi，xj）间的相关函数，此相关函数为高斯函数.

相关函数的形式如下：

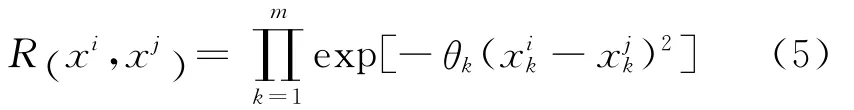
式中：θk为各向异性参数.

在预测点x0处的预测响应值和预测标准差分别为

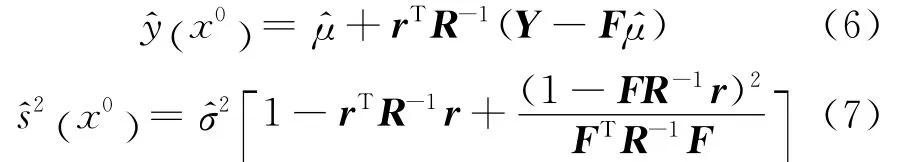
相关函数R （xi，xj）及和均依赖于各向异性参数θ，因而构建Kriging模型的关键在于θ的求解，通常由极大似然估计给出，即在θ＞0的情况下使式（8）取得极大值.通过求解得到各向异性参数θ后，即完成了整个Kriging代理模型的构建.

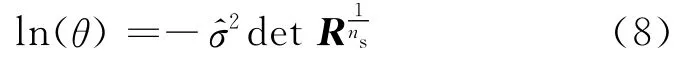
1.2 参数化叶型

对叶型进行参数化表达是实现自动优化设计的前提，一般二维叶型的参数化主要有2种方法：中弧线加厚度分布和采用构造曲线直接对叶型压力面、吸力面型线进行参数化.目前常用的构造曲线主要有3种：Bézier曲线、均匀有理B样条曲线和非均匀有理B样条即NURBS曲线［11］.其中Bézier曲线由于形式简单、易操作，在参数化中得到广泛应用.

采用2段Bézier曲线分别对某涡轮叶型压力面和吸力面型线进行参数化，共有16个控制点控制叶型形状.其中位于原点处的控制点为2段Bézier曲线的公共点，吸力面型线由自公共点顺时针连接的10个控制点获得，而压力面型线由自公共点逆时针连接的7个控制点获得.图2为叶型型线及对应控制点连线示意图，其中x和y分别表示叶型的轴向和周向位置.对叶型进行气动优化设计时，通过改变控制点位置即可生成新的叶型，直到获得设计变量空间下目标函数最优时的叶型，完成叶型优化改进.

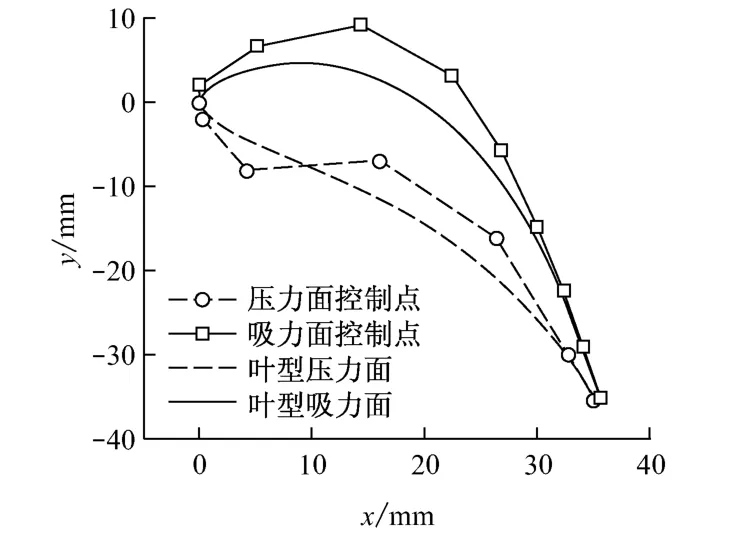
图2 叶型型线及对应控制点连线Fig.2 Profile of the airfoil and polyline of airfoil control points

1.3 数值方法

在网格生成时选用HOH型拓扑结构：进口段为H型结构化网格，叶型处为O型结构化网格，考虑到实际流动情况，出口段选择I型网格.对近壁面处网格进行加密，使叶片壁面第1层网格满足y＋＜10.图3给出了叶型前缘和尾缘处的网格.

图3 叶型前缘和尾缘处的网格Fig.3 Mesh for the leading and trailing edge of airfoil

对要进行气动优化研究的涡轮叶型构造平面叶栅，叶栅栅距为50mm.数值计算时给定进出口边界条件，其中进口处给定平均总压为2×106Pa，进口总温为573K，进口来流气流角为5°；在出口处给定平均静压，使得出口静压与进口总压比为0.896.湍流模型选择一方程的Spalart－Allmaras湍流模型（即S－A湍流模型），空间离散采用二阶精度的迎风格式，时间项推进采用四阶Runge－Kutta法加速迭代求解.最大迭代步数设为5 000，收敛标准设为全局残差降到10－6以下.

为验证本文数值方法的可靠性，选取文献［12］中出口气流角为67°的直叶片进行校核.该文献采用试验手段和理论计算对不同出口气流角的叶栅进行气动性能的研究，给出了详细的叶片几何数据和试验数据.根据上述数据生成叶栅网格，采用S－A湍流模型和二阶精度的迎风格式在设计工况下进行数值模拟.图4给出了中径处叶片表面临界速度比沿相对轴向弦长的分布对比.由图4可以看出，数值计算所得结果与试验数据吻合较好，从而验证了数值计算方法的可靠性.

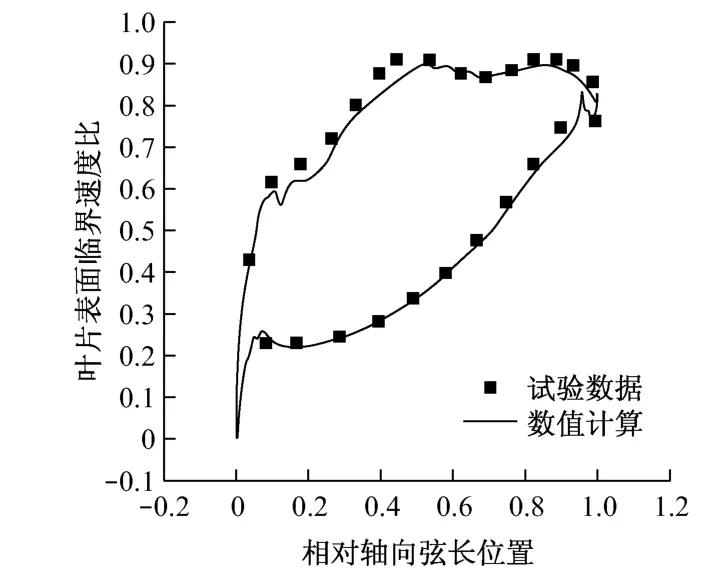
图4 中径处叶片表面临界速度比分布对比Fig.4 Comparison of surface critical velocity ratio at mid－span height between experimental and numerical data

2 涡轮叶型优化设计

采用2组Bézier控制点控制型线变化，其中O点为压力面型线和吸力面型线的公共控制点，如图5所示.在生产实践中，常通过微调叶片的头部型线来满足不同设计要求下进出口流动角的变化，为此需要研究工程设计中对头部型线的微调是否合理及是否存在最优头部型线.以对叶型头部控制点的优化为例，采用上述气动优化设计方法，研究其对叶型气动性能的优化设计.设定原始叶型控制点A和B到O点的距离分别为R1和R2，控制点变化后对应的距离为r1和r2.优化时为保证叶型几何进气角不变，只改变OA和OB2段控制线的长度而不改变其角度，即以系数矩阵L作为设计变量，以压力恢复系数ξ最大为优化目标进行叶型的优化设计.

图5 叶型前缘控制点Fig.5 Control points at leading edge of profile

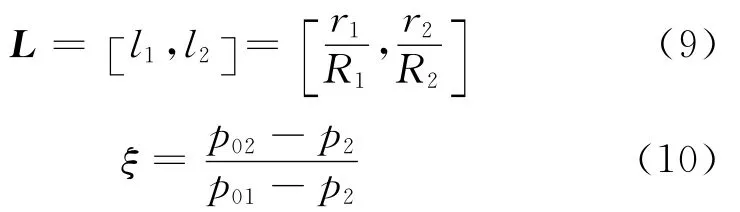
系数矩阵L与压力恢复系数ξ的定义如下式中：p01和p02分别为平面叶栅进口和出口的总压；p2为出口静压.

涡轮叶型气动优化问题可以用式（11）来表示

利用试验设计方法和U＊10（108）均匀设计表生成10个初始样本点，使样本点在试验空间里均匀分布，并构造初始化代理模型，进而对优化目标进行寻优.图6给出了整个优化过程中响应值随迭代步数的变化.

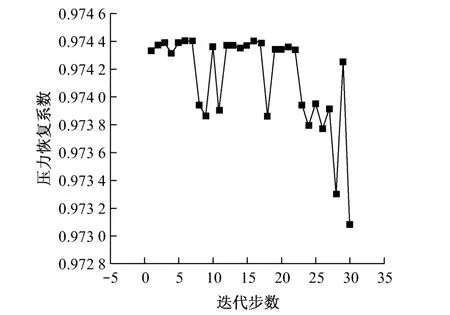
图6 响应值随迭代步数的变化Fig.6 Response of pressure recovery coefficient to iteration step

设计工况下原始叶型的压力恢复系数ξ0＝0.973 76，通过优化迭代后得到当设计变量L＝［1.800 000，1.032 544］时，总压恢复系数达到最大，即ξ1＝0.974 40，压力恢复系数有所增大.优化结果表明，存在最优头部型线，但压力恢复系数增大的程度有限；同时也说明了实际工程设计中所采用的头部型线微调方法的合理性.图7给出了优化前后控制点及型线的对比.从图7可以看出，叶型前缘处控制线段长度优化的主要变化集中在吸力面型线上，压力面型线整体上保持不变.

为进一步分析叶型前缘型线的变化对流场的影响，图8给出了原始叶型和优化叶型表面压力系数Cp沿轴向的分布，其中表面压力系数Cp定义如下

式中：p为当地静压；p0为叶栅进口平均静压；p＊0为叶栅进口平均总压.

图7 优化前后控制点及型线的对比Fig.7 Comparison between original and optimized profile

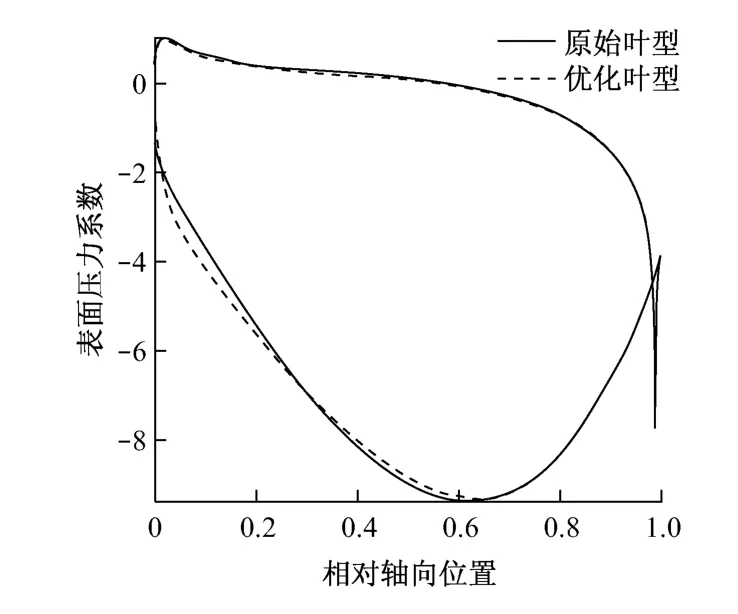
图8 原始叶型和优化叶型表面压力系数沿轴向的分布Fig.8 Comparison of pressure coefficient between original and optimized airfoil

从图8可以看出，优化前后叶型压力面上的表面压力系数分布规律基本一致；而在吸力面上存在明显的差异，优化叶型靠近前缘吸力面处的表面压力系数较小，气流沿吸力面流动时压力变化较平缓.叶型前缘变化引起的流动变化使得叶型型面损失减小，压力恢复系数有所增大，达到了优化叶型、提高叶栅性能的目的.

3 结 论

基于自适应Kriging代理模型，设计开发了一套集参数化建模、优化算法和数值求解于一体的自动叶型气动优化设计系统.利用该系统对某涡轮叶型头部型线进行了优化设计，使原始叶型的压力恢复系数进一步增大，结果表明存在最优头部型线，说明了工程实践中对头部型线调整的合理性.经过优化改善了叶型的性能，同时也验证了整个优化系统的可靠性，为叶片的全三维优化设计、提高叶片及级性能的研究奠定了基础.

［1］BURGUBURU S，TOUSSAINT C，BONHOMME C.Numerical optimization of turbomachinery bladings［J］.Journal of Turbomachinery，2004，126（1）：91－100.

［2］ZHOU Fangzhen，FENG Guotai，JIANG Hongde.The development of highly loaded turbine rotating blades by using 3doptimization design method of turbomachinery blades based on artificial neural network＆genetic algorithm［J］.Chinese Journal of Aeronautics，2003，16（4）：198－202.

［3］OYAMA A，LIOU M S，OBAYASHI S.Transonic axial flow blade optimization：evolutionary algorithms／three dimensional Navier－Stokes solver［J］.Journal of Propulsion and Power，2004，20（4）：612－619.

［4］ÖKSÜZÖ，AKMANDOR˙I.Turbine blade shape aerodynamic design using artificial intelligence［C］／／ASME Turbo Expo.Reno－Tahoe，Nevada：ASME，2005.

［5］王红涛，竺晓程，杜朝辉.自适应Kriging近似模型及其在二维扩压器优化设计中的应用［J］.计算力学学报，2011，28（1）：15－19，24.WANG Hongtao，ZHU Xiaocheng，DU Zhaohui.Applications of adaptive Kriging approximation model in two dimensional diffuser aerodynamic optimization design［J］.Chinese Journal of Computational Mechanics，2011，28（1）：15－19，24.

［6］薛亮，韩万金.基于遗传算法与近似模型的全局气动优化方法［J］.推进技术，2008，29（3）：21－26.XUE Liang，HAN Wanjin.Global aerodynamic optimization method using genetic algorithms and surrogate model［J］.Journal of Propulsion Technology，2008，29（3）：21－26.

［7］高行山，韩永志，张娟，等.基于近似技术的涡轮叶片气动优化设计［J］.计算力学学报，2008，25（6）：874－877.GAO Hangshan，HAN Yongzhi，ZHANG Juan，et al.Blade aerodynamic optimization design based on approximation method［J］.Chinese Journal of Computational Mechanics，2008，25（6）：874－877.

［8］MENGISTU T，GHALY W，MANSOUR T．Aerodynamic shape optimization of turbine blades using a design－parameter－based shape representation［C］／／ASME Turbo Expo．Montreal，Canada：ASME，2007．

［9］王红涛．汽轮机低压排汽系统内部流动及其气动优化设计研究［D］．上海：上海交通大学，2011．

［10］王红涛，竺晓程，杜朝辉．基于Kriging代理模型的自适应序贯优化方法［J］．计算机工程与应用，2009，45（26）：193－195．WANG Hongtao，ZHU Xiaocheng，DU Zhaohui．A－daptive sequential optimization algorithm based on Kriging surrogate model［J］．Computer Engineering and Applications，2009，45（26）：193－195．

［11］乐英，王璋奇，韩庆瑶．基于非均匀有理B样条曲面重构汽轮机扭曲叶片［J］．动力工程学报，2010，30（12）：926－931．YUE Ying，WANG Zhangqi，HAN Qingyao．Reconstruction of turbine blade twisted based on NURBS surface［J］．Journal of Chinese Society of Power Engineering，2010，30（12）：926－931．

［12］SCHWAB J R．Aerodynamic performance of high turning core turbine vanes in a two－dimensional cascade［C］／／AIAA／SAE／ASME 18th Joint Propulsion Conference．Cleveland，Ohio：AIAA，1982．