震源深度对地震动方向性特征的影响
2014-09-21胡进军章文波谢礼立
胡进军,章文波,谢礼立
(1.中国地震局工程力学研究所中国地震局地震工程与工程振动重点实验室,150080哈尔滨;2.中国科学院大学地球科学学院,100049北京;3.哈尔滨工业大学土木工程学院,150090哈尔滨)
地震产生的地震动是震源、传播路径和场地条件的函数,它受到与此诸多因素的影响和控制.近断层地震动由于靠近震源,更容易受到震源参数的影响,可能会表现出一些不同于远场地震动的特征,比如地震动时程中的大脉冲、永久位移或者丰富的高频分量等;另外还有地表地震动场分布的方向性、上/下盘差异等特征[1-6].而在工程中对于地震动预测时,一般将震源项主要用震级参数来考虑,但是即使相同的震级,由于震源机制、震源深度等的不同,其产生的地震动也可能有很大差别.研究表明,相同震级和距离的情况下,逆断层或逆冲断层地震比正断层地震引起更大的地面运动,而走滑断层地震引起的地面运动介于两者之间[7].除了在地震动的幅值上有差别外,由于震源的辐射机制和传播路径的不同,也会造成地表地震动分布的不均匀特性.比如由于断层的破裂速度和地壳介质的剪切波速接近而引起的破裂传播效应,继而造成的地震动方向性分布特征.使得在断层破裂传播的前方,地震动幅值比较大且衰减的比较慢,因而形成破裂两端非对称的分布;另外对于倾滑断层,还可能造成地震动在上下盘的明显差异.因此,显然分析震源对地震动的影响,还要考虑除了震级以外的其他参数.研究震源参数对地震动影响的最直接手段就是对实际地震动进行统计和分析,但是由于受到实际强震数据有限性的制约,并且每次实际地震的震源参数都不相同,很难有可比性.因此,本研究采用数值模拟方法计算不同震源深度情况下的地震动,分析其对地震动及其空间分布特征的影响.
1 数值模拟
研究采用离散波数有限元方法[8]计算不同震源深度的地震产生的地震动,此方法首先求解地震波在介质中传播的格林函数,然后再根据表示定理计算有限断层产生的地震动[9].此方法可以考虑震源参数的变化引起的近断层地震动,而且断层破裂过程可以设置的较为复杂.与其他有限断层和水平成层介质中计算地震动的方法相比,此方法的计算结果考虑了地震动的P波、S波和面波以及近场项,而且计算效率比较高,因此耗时也比较少.为了从方向性角度分析震源深度对地震动的影响,震源采用简单的垂直走滑断层模型,震级依据对具有单一走滑震源机制的70个地震的统计结果设定为MW6.4 级,断层的长和宽根据经验统计关系[5,10-11]设定为26 km和10 km,其他震源参数见表1和图1.通过改变断层的上界埋深,并假定震源位于断层宽度的中心,从而改变震源的深度.断层上界埋深h 分别设置为0.1、1.0、3.0、5.0 和10.0 km.了更好地模拟产生方向性效应的条件,将破裂速度设置的接近剪切波速,即假定破裂速度Vr为剪切波速Vs的0.9倍.地壳介质模型采用水平成层的速度结构[12],自由地表的观测点成网格状沿断层两侧和走向分布.

表1 断层模型参数

图1 断层模型示意
2 数值结果分析
表2给出了不同震源深度的地震动峰值加速度值.其中Xs定义为沿着断层走向的距离.震中位置为坐标原点,沿着破裂传播的方向为正方向,反之为负方向.从图2的图形可知,震源深度对地震动的影响很大,不仅影响幅值的大小,还影响到波形和强震段的持时特征.震源越深观测点的地震动峰值越小,并且随着震中距的增大二者差别越大.但是仅从时程和波形很难全面了解震源深度对地震动的影响,还需要对其不同参数进行定量分析.
基于上述震源模型,计算不同震源深度下的地震动,考虑到地震动不同分量的差异性,分别计算垂直于断层、平行于断层以及竖向地震动三分量加速度时程.然后基于数值模拟的结果分析震源深度对地震动的峰值、反应谱和持时等参数的影响.
2.1 地震动整体特征分析
为了分析不同震源深度的地震对地表的地震动时程的影响,将不同震源深度下的地震动时程进行对比.选取上界埋深0.1 km和5.0 km(即震源深度5.1 km和10 km)的两种情况的地震动时程进行对比.图2以水平分量为例给出了与断层走向平行排列的一行观测点的加速度时程曲线,
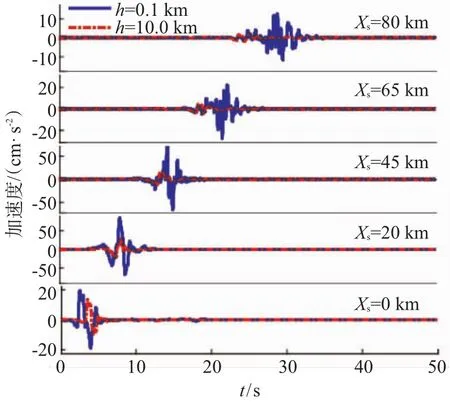
图2 不同震源深度对地震动时程的影响

表2 不同震源深度的地震动峰值加速度 cm·s-2
2.2 地震动峰值特征分析
地震动峰值加速度是反应地震动强度的重要参数,研究表明地震动的峰值由于受到破裂传播效应的影响,在破裂前方的地震动幅值比较大,而后会随着距离逐渐衰减[3,5,13].为了分析不同震源深度是否对此特征有影响,图3(a)以地震动水平分量为例给出不同震源深度下地震动峰值沿断层走向距离的变化.分析表明震源深度越浅,即震源越靠近地表,地震动的峰值越大,而且无论是在破裂传播的前方还是后方都有此特征.但是为了分析震源深度是否对方向性的大小有影响.比较了破裂前后方地震动幅值和破裂初始位置地震动幅值的比值,一般认为地表破裂初始位置的地震动不受破裂传播效应的影响.将不同距离处的地震动峰值与破裂初始位置的幅值进行对比,得到峰值比,通过峰值比沿走向的变化曲线反应震源深度对方向性效应的影响,结果见图3(b).分析表明,不同震源深度的地震动均出现明显的方向性特征;而且,通过峰值比反映出来的方向性效应并没有随着震源深度的增加而减弱.

图3 不同震源深度下地震动沿断层走向变化
为了分析震源深度对整个地震动分布场特征的影响,图4以两个水平分量为例给出了地震动场的变化.其中(a)、(b)为垂直于断层的分量;(c)、(d)为平行于断层的分量.结果表明:震源深度对地震动空间分布场影响显著.虽然随着震源深度的增加地震动场的幅值在减弱,但是破裂前后方的差异依然非常明显.震源深度的变化对地震动的不同分量都有影响,但是其对地震动的垂直断层的分量比较大.而且在破裂传播方向上存在一个典型区域,此区域的地震动比其他区域要大得多,而且衰减的也比较慢.
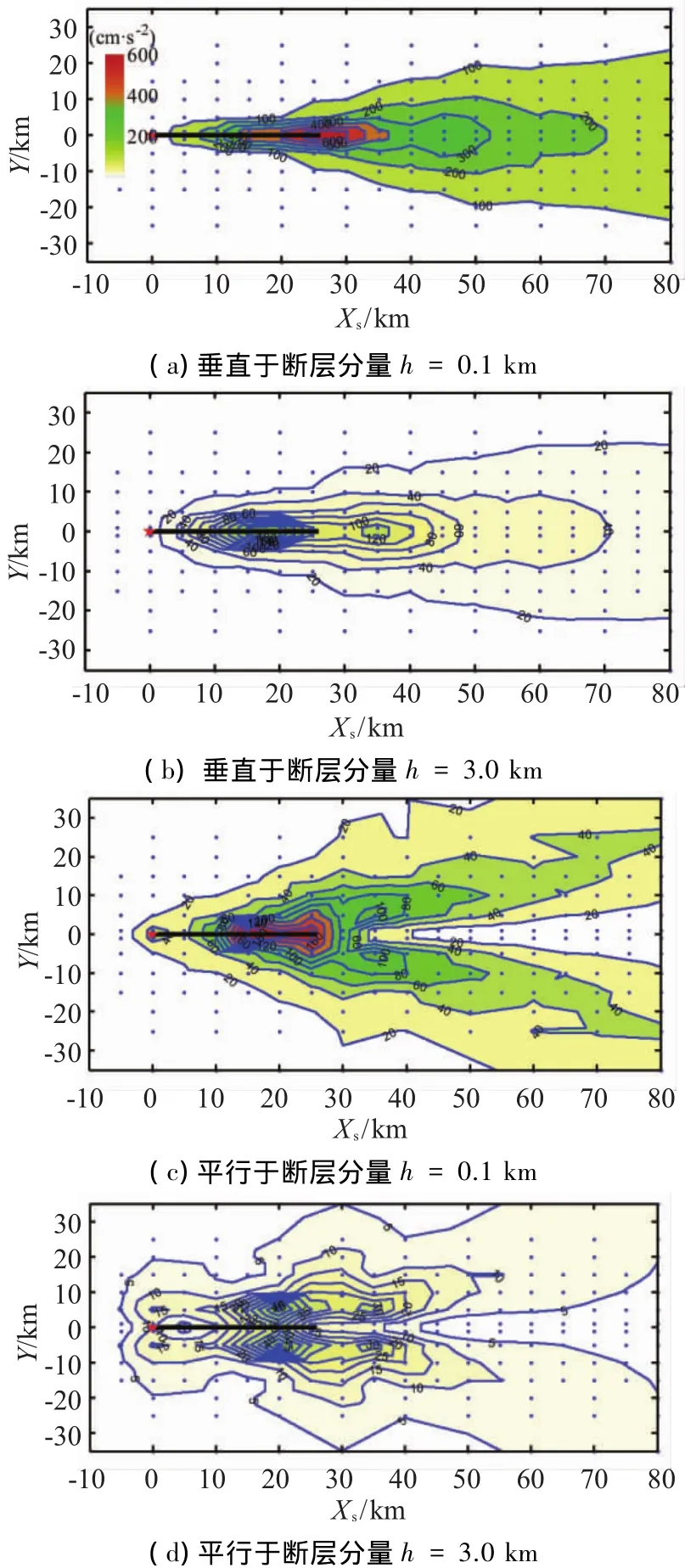
图4 不同震源深度的地震动峰值分布场
2.3 地震动反应谱特征分析
将不同震源深度下沿断层走向分布的一行观测点的地震动反应谱表示在图5中,以水平分量为例,给出了3种震源深度 (0.1、3.0和10.0 km)的对比.T代表反应谱的周期,Sa代表反应谱值.结果表明:不同震源深度的加速度反应谱值均在破裂开始处随着距离增加而迅速增加,并且不同深度地震的反应谱沿着破裂方向的变化趋势接近,即垂直断层分量的反应谱整体衰减很慢,平行断层分量和竖向分量的反应谱在通过了断层末端一段距离后迅速衰减.
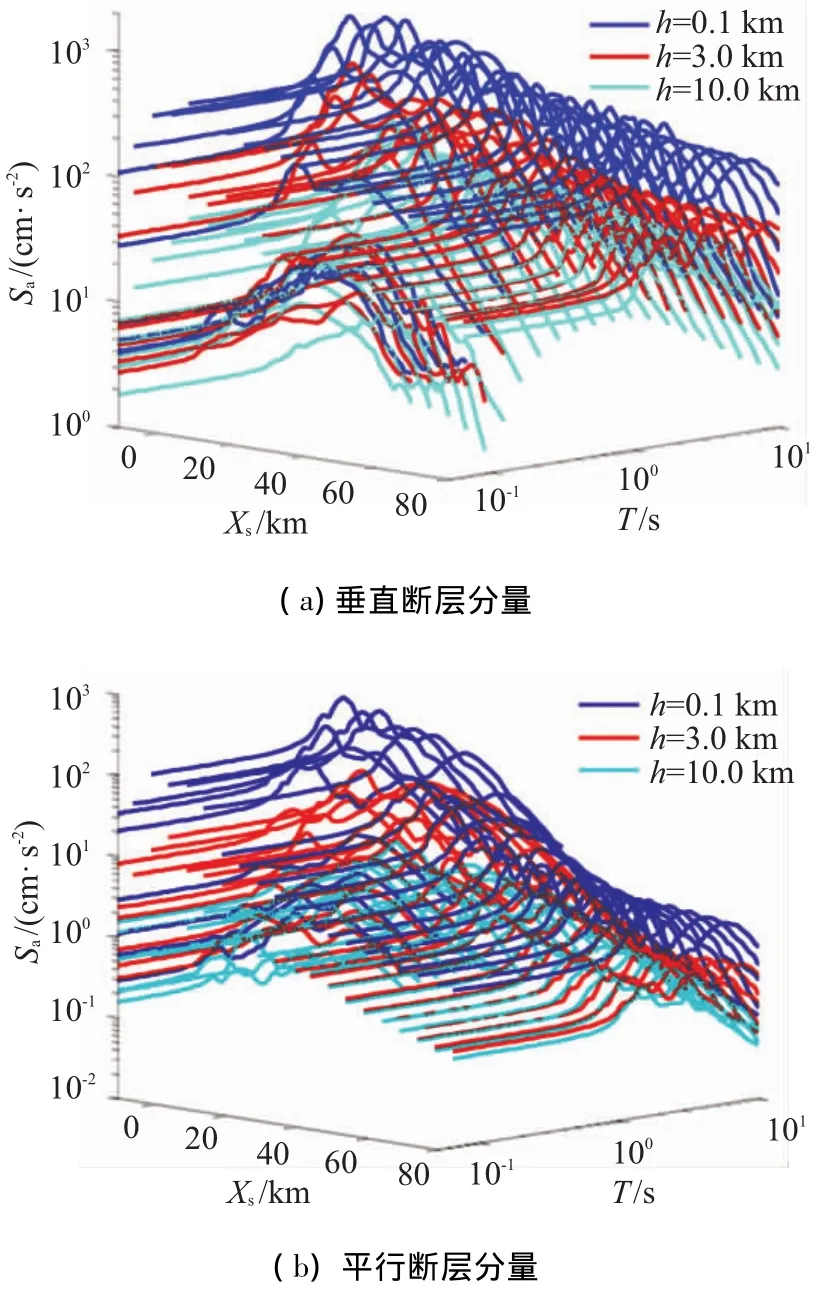
图5 不同震源深度的加速度反应谱沿断层走向的变化
2.4 地震动持时特征分析
研究选取工程中常用的地震动相对能量持时[14],分别从持时沿着断层走向的变化和整个地表观测点的持时分布场的角度分析了震源深度对方向性效应的影响.选取沿着断层走向分布的一行观测点在不同震源深度时的加速度持时进行分析,并将不同震源深度时持时表示在图6中.图6(a)以垂直断层分量为例,给出持时对比图.结果表明:一方面,不同震源深度的持时均在破裂前方受到方向性效应显著影响的区域有最小值,而后随着沿断层走向的距离逐渐增大;另一方面,从不同分量的持时随深度的变化特征来看,垂直于断层的分量随着震源深度的增大在破裂前方的持时有增大的趋势,在破裂后方持时有减小的趋势.震源的深度对平行于断层分量的影响也有与垂直断层分量类似的特点,但是震源深度对竖向分量的持时影响不大.另外,不同震源深度下地震动持时场的分布特征分析表明,地震动的持时在破裂前方较小,在破裂的后方较大;且随着震源深度的增加,在破裂前方的持时有增加的趋势.图6(b)给出了一个典型的持时场分布图(h=10.0 km).

图6 地震动持时随震源深度的变化
3 结 论
1)对于典型的垂直走滑断层,存在明显的地震动方向性特征,在断层破裂的前方,相同震中距的观测点的地震动的峰值和反应谱值明显大于破裂后方的幅值;强震动持时则相反,在破裂后方的持时要高于破裂前方的持时.
2)震源深度对地震动的峰值参数有明显影响.一方面,随着震源深度的增大,地震动的峰值降低.另一方面,虽然随着震源深度的增加地震动的峰值降低了,但是方向性特征并没有减弱,也就是破裂传播的前方和后方的地震动参数的方向性差异依然存在.
3)数值模拟中往往是基于对震源、传播介质、和场地的简化模型进行的,而实际地震中的地震动及其空间分布有很大的随机性,因此实际地震动不可能与数值模拟的结果完全相同,但是通过简化的模型得到的结果仍然可以作为定量研究的参考,来补充实际地震动记录的不完备性,进而为进一步建立地震动经验合成方法提供理论依据.
[1]ABRAHAMSON N A,SOMERVILLE P G.Effects of the hanging wall and footwall on ground motions recorded during the Northridge earthquake[J].Bulletin of the Seismological Society of America,1996,86(18):593-599.
[2]ABRAHAMSON N A,SILVA W J.Empirical response spectral attenuation relations for shallow crustal earthquakes[J].Seismological Research Letters,1997,68(1):94-127.
[3]SOMERVILLE P G,SMITH N F.Forward rupture directivity in the Kobe and Northridge earthquakes,and implications for structural engineering[J].Seismological Research Letters,1996,67(2):55.
[4]SOMERVILLE P G,SMITH N F,GRAVES R W.Modification of empirical strong ground motion attenuation relations to include the amplitude and duration effects of rupture directivity[J].Seismological Research Letters,1997,68(1):199-222.
[5]SOMERVILLE P G,IRIKURA K,GRAVES R.Characterizing crustal earthquake slip models for the prediction of strong ground motion [J].Seismological Research Letters,1999,70:59-80.
[6]AAGAARD B T,HALL J F,HEATON T H.Characterization of near-source ground motion with earthquake simulations[J].Earthquake Spectra,2001,17(2):177-207.
[7]MCGARR A.Scaling of ground motion parameters,state of stress,and focal depth [J].Journal of Geophysical Research,1984,89(B8):6969-6979.
[8]OLSON A H,ORCUTT J A,FRAZIER G A.The discrete wavenumber/finite element method for synthetic seismograms[J].Geophys J R Astr Soc,1984,77:421-460.
[9]SPUDICH P,XU L.Software for calculating earthquake ground motions from finite faults in vertically varying media[M]//International Handbook of Earthquake and Engineering Seismology.New York:Academic Press,2003:1633-1634.
[10]WELLS D L,COPPERSMITH K J.New empirical relationships among magnitude,rupture length,rupture width,rupture area,and surface displacement[J].Bulletin of the Seismological Society of America,1994,84:974-1002.
[11]HANKS T C,KANAMORI H.A moment magnitude scale[J].Journal of Geophysical Research,1979,84(B5):2348-2350.
[12]胡进军.近断层地震动方向性效应及超剪切破裂研究[D].哈尔滨:中国地震局工程力学研究所,2009.
[13]SOMERVILLE P,SAIKIA C,WALD D.Implications of the Northridge earthquake for strong ground motions from thrust faults[J].Bulletin of the Seismological Society of America,1995,86:5115-5125.
[14]TRIFUNAC M D,BRADY A G.A Study on the Duration of Strong Earthquake Ground[J].Bulletin of the Seismological Society of America,1975,65(3):581-626.
