一种改进的群目标自适应跟踪算法

李振兴，刘进忙，李 松，李延磊

(空军工程大学防空反导学院，710051西安)

人们提出了许多重要的目标跟踪理论和方法，其中大多数方法将目标作为一个点源目标来处理.而在海面目标监控、多目标编队跟踪等许多跟踪场景内，跟踪对象通常由一系列具有类似运动方式的空间临近目标组成，即称作为群目标［1］.此时群目标跟踪会受到许多特殊因素的影响［2-3］，主要包括量测数目和观测模式的不确定变化.前者是由于传感器分辨率限制和传感器-目标的位置变化等因素影响，群目标的量测数目是时变的，影响了传统跟踪算法的正常进行;而后者主要是由于“一个目标对应一个量测”的观测模式被打破，导致个体目标航迹关联的模糊性.

针对上述问题，人们提出对群的整体进行跟踪的思想.根据这一思想，主要包括概率假设密度(PHD)滤波法［4-6］和 Bayesian 递推算法［3，7-11］.其中，PHD滤波法可以有效跟踪未知数目的空间临近目标，并同时解决数据关联问题，适合解决多个群目标的跟踪问题.它的不足在于当算法估计单元范围内目标的期望数目时，无法内在区分假设密度传播中哪部分是由于估计不确定或因群目标扩展产生的［7，9］.另外，PHD 方法推导很复杂，不利于实际应用推广.而在Bayesian递推算法方面，Koch［3］针对单个群目标的跟踪问题，提出利用群的质心状态和扩展状态来描述群的整体运动.它的假设前提是相比群的扩展状态，可以忽略传感器的量测误差影响.文献［7-9］提出在不忽略量测误差情况下的Bayesian递推算法.由于考虑了量测误差，导致不能直接采用文献［3］在状态单维上的滤波更新算法，需要在全维上进行综合处理，因而需要采用大量启发式的假设条件.文献［10］提出利用变分贝叶斯推理方法，推导了一组更加严格的群目标量测更新公式，有效提高了跟踪精度，但它没有考虑跟踪模型和扩展状态预测参数的进一步优化.文献［11］对文献［3］的模型进行了进一步论证，尤其针对群质心状态的边缘后验概率密度进行了重新推导，修正了群质心状态的更新协方差表达式.

针对上述分析，本文在文献［3］算法的基础上，将文献［10］的变分贝叶斯迭代法引入滤波过程中，提出一种改进的群目标自适应跟踪算法.重点针对群质心跟踪模型和扩展状态预测参数的优化问题，包括自适应调整群质心的过程噪声方差和质心状态协方差估计，以及利用模糊推理方法自适应输出扩展状态的预测值.最后通过仿真实验验证了本文算法的有效性.

1 Bayesian群跟踪算法

依据文献［3］的严格数学推导，群目标的每个量测可以等效为群质心量测通过扩展状态下散射的结果.通过跟踪群目标的质心运动状态和扩展状态，可以将一群空间临近目标(CSO)等效成单个个体目标，在实际处理中方便了对群目标复杂态势下的跟踪.文中的群目标跟踪算法是建立在正确数据关联问题的基础上，重点解决群目标的航迹维持问题.

1.1 量测似然函数的构建

文献［3］利用随机变量xk代表群质心的运动状态，分别表示群质心的位置、速度和加速度．利用对称正定(SPD)矩阵Xk代表群整体的扩展状态，即在二维平面内用一个椭圆来描述群的整体形状(三维空间为椭球状)．量测用来表示(仅包括目标位置)，量测转移矩阵H=［Ⅰd，0d，0d］(d表示空间维数，d=2 代表二维空间)，因此k时刻的量测方程为

式中:k时刻的量测集为k时刻的量测数目．文献［3］认为相比扩展状态的影响，可以忽略传感器的量测误差的影响．因此，噪声假设为均值为零，方差为Xk的高斯白噪声．另外，k时刻的累积量测集为因此，量测似然函数为

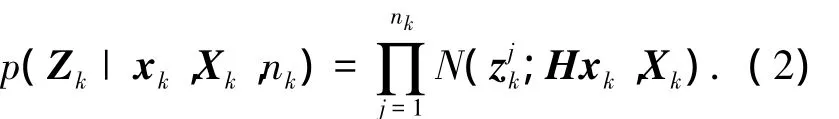
式中:N(x;μ，Σ)代表均值μ，方差Σ的正态分布．引入量测均值和对应的散射矩阵k为

1.2 联合状态的先验概率密度的构建

xk和Xk的联合先验概率密度为

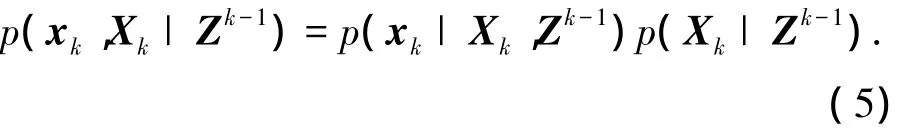
式中:向量xk的条件概率密度为

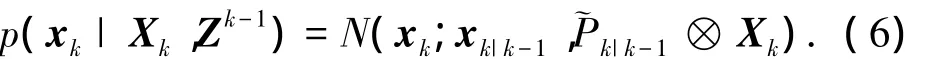
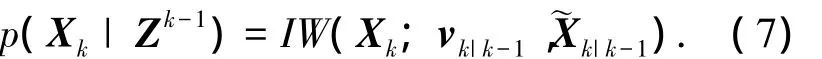
矩阵Xk的条件概率密度为表示均值为A/(a-d-1)的逆Wishart分布函数，a为自由度且满足a-d-1＞0．

由式(7)可得

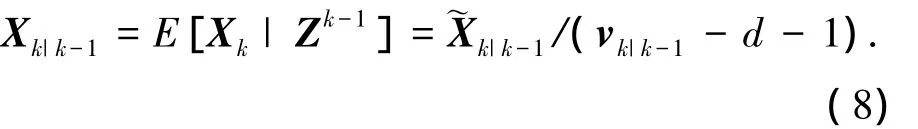
因此，对应的Bayesian滤波的一步预测公式为

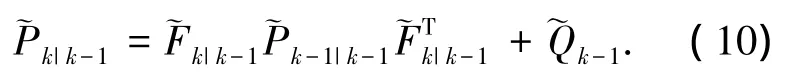
假设Xk|k-1=Xk-1|k-1，可得

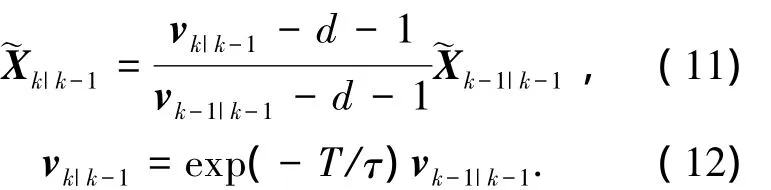
式中:T代表传感器采样周期，τ代表扩展状态的变化率，定量反映了扩展状态随时间变化的灵敏度．

1.3 联合状态的后验概率密度的构建

xk和Xk的联合后验概率密度为

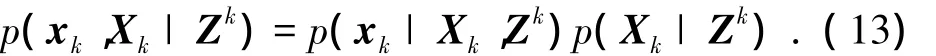
量测转移矩阵

新息协方差

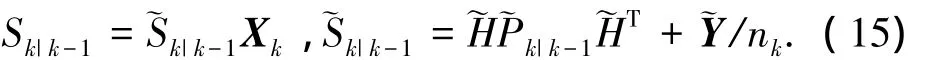
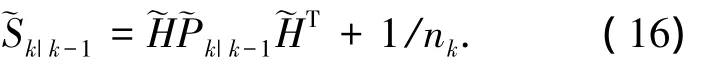
滤波增益

从式(17)中可知，滤波增益Kk|k-1与Xk是独立的．因此，对应的运动状态更新公式为

扩展状态更新公式为

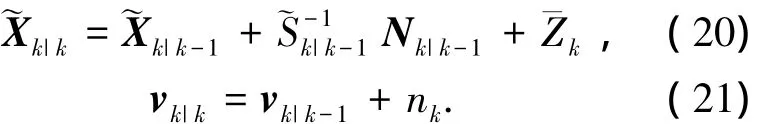
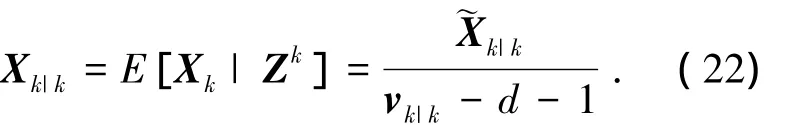
式(18)中xk|k是由群质心的条件后验概率密度p(xk|Xk，Zk)推导而来，为获得xk的更加准确的估计值，则有必要推导出xk的边缘后验概率密度p(xk|Zk)进行计算．xk的均值［11］

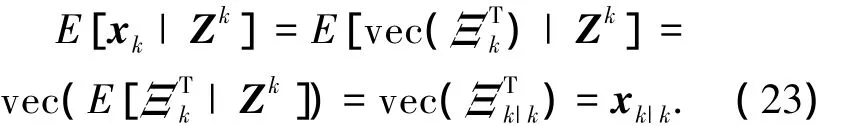
由式(23)可知，由p(xk|Zk)推导的xk的估计值与由p(xk|Xk，Zk)推导的估计值相等．

xk的估计误差协方差

尽管预测式(9)、(10)和更新公式(18)、(19)形式上类似于Kalman滤波公式，但不同之处在于k|l和都是仅作为一维空间内的跟踪滤波参数，与之相对应的滤波增益k|k-1独立于扩展状态Xk．而过程噪声⊗Xk表明质心的运动和群目标的扩展状态Xk之间存在一种非常特殊的关系，即规模越大的群目标的运动不确定性越大，群的行为越难以预测．

2 群目标自适应跟踪算法

2.1 问题分析

通过分析可知，文献［3］重点在于推导xk和Xk的滤波更新步骤，而忽略了跟踪模型和扩展状态预测参数的优化．本文通过大量仿真实验验证，这两者的优化对群目标的跟踪结果同样具有重要的影响．具体表现在以下几个方面:

1)文献［3］的方法是建立在Singer模型的基础上，这种模型在群目标匀速飞行的过程中，可以取得比较好的跟踪效果.但是一旦群目标发生机动时，比如转弯运动时，跟踪效果会变差.而“当前”统计(CS)模型对机动目标的跟踪效果较好，因此，可以考虑采用“当前”统计模型用于对群质心的跟踪.

2)群扩展状态Xk的估计主要是受群目标量测和扩展自由度的影响．文献［3］在估计Xk时，将扩展自由度按照先验知识设定成一个固定参数．当群目标发生机动时，此时群目标的扩展状态会发生变化，采用固定参数的方法会导致较大的估计误差．因此，需要考虑对扩展自由度进行自适应调整．

3)群目标的机动形式还包括群的分裂和合并，而一旦群产生分裂或合并时，群的质心状态和扩展状态会发生很大的变化，因此需要及时增加或删除群目标的跟踪航迹，否则会带来很大的跟踪误差.因此，需要寻找一种简单快速的判定方法，可以迅速判别群目标是否发生分裂或者合并.

2.2 群质心运动模型

CS模型主要依赖于模型自身的两个参数:加速度极限值和机动频率.当两者取值过大时，则跟踪匀速运动或者不具有较大机动加速度目标时其性能较差;取值较小时则跟踪突发强机动目标时其收敛速度较慢，算法的实时性降低，一旦目标机动超过预先设定的值，其跟踪性能将明显恶化.因此利用MCS模型来描述群质心的运动，利用群质心的速度预测值和估计值间的偏差对系统噪声方差进行自适应调整，确保算法可以有效跟踪群的匀速或弱机动情况;并引入强跟踪滤波中的渐消因子，利用残差信息对质心状态协方差进行修正，确保算法有效跟踪群的突发机动情况.

群质心的状态转移方程:

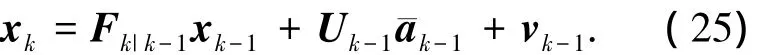
式中:T为采样周期，α为机动时间常数的倒数(机动频率)．另外，过程噪声，且有

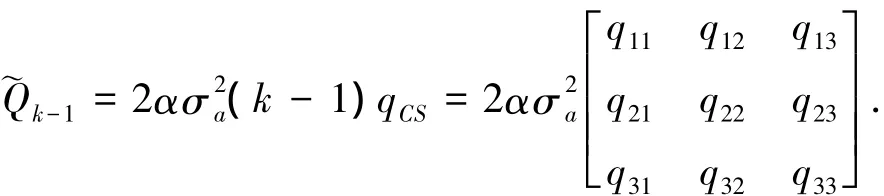
因此，修正后的系统噪声方差为式(29)．式中，β为大于零的量纲变换系数．

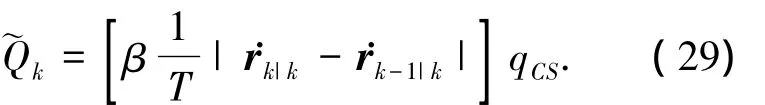
针对群目标发生突发机动时，式(10)中预测误差协方差Pk|k-1不能随残差改变的缺点，引入强跟踪滤波器中的时变渐消因子［13］．依据目标运动情况实时调整增益，强迫输出残差近似为高斯白噪声，最大限度提取输出残差中的有效信息，因此设置的渐消因子为

其中，

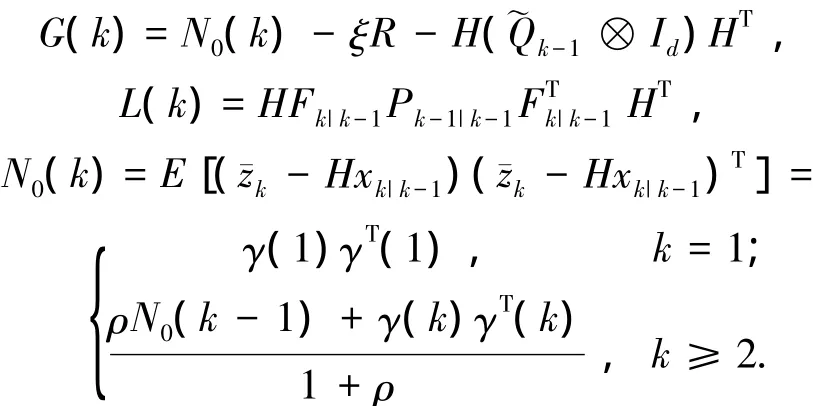
式中:γ(k)=zk-Hxk|k-1，γ(1)是初始残差;ρ(0＜ρ≤1)是遗忘因子，一般取ρ=0.95;ξ(ξ≥1)是弱化因子，可以使状态估计值更加平滑．

因此，修正后的Pk|k-1为

2.3 扩展状态预测参数的自适应输出

由前述可知，扩展状态的预测是通过逆Wishart分布的自由度的调整来实现［9-10］:由式(12)可知，τ为一时间参数，反映的是扩展状态随时间变化的敏捷度．假设f(τ)为扩展状态预测参数，即f(τ)=exp(-T/τ)．通过采用模糊推理的方法［14-15］，将扩展状态对应的椭圆面积预测值和估计值的偏差以及偏差变化率作为模糊输入量，从而计算出f的输出值．具体步骤如下:

1)输入参数的归一化

由于Xk的特征值对应着扩展椭圆半轴长的平方，因此不妨假设Xk的特征值为λ1和λ2(d=2)，则对应的扩展椭圆的面积下标和X下标相对应)．定义扩展椭圆相对面积差

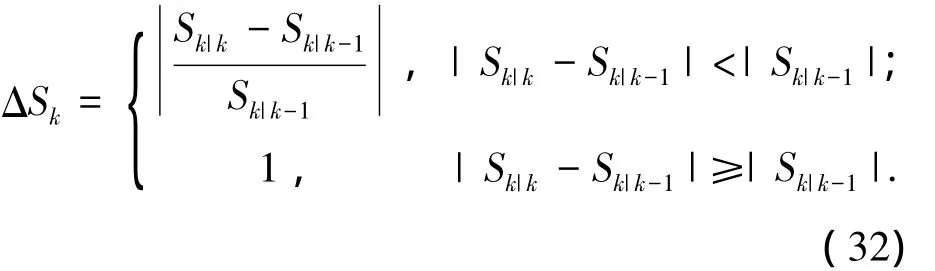
定义扩展椭圆面积差变化率

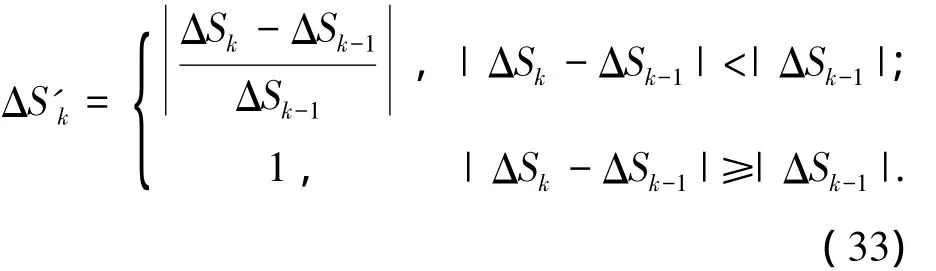
2)输入参数的模糊化

定义输入变量 ΔS和 ΔS'的模糊集为 ZE(零)，SP(正小)，MP(正中)，LP(正大).隶属度函数采用梯形函数，见图1所示.

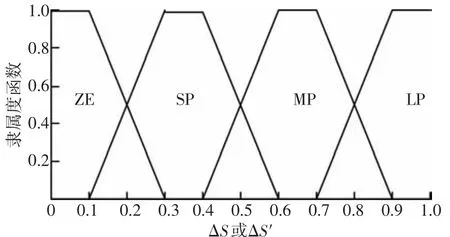
图1 ΔS和ΔS'的隶属度函数

3)模糊逻辑规则的设置

确定输出f的值域.由于T/τ＞0，可得0＜f(τ)＜1．将输出变量的模糊集为分ZE，SP，MP，LP，VP(正很大)，EP(正极大)，制定模糊推理规则，如表1所示.

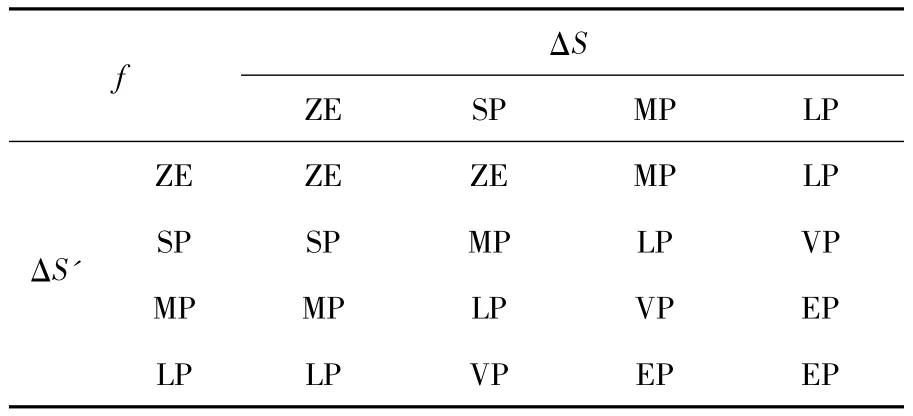
表1 f的模糊关系

①f随着输入变量ΔS和ΔS'的增大而增大;

②当ΔS和ΔS'属于模糊集ZE或者SP时，表明群目标整体机动变化很小，此时扩展状态的预测参数值可信度很大，表1选择模糊集ZE和SP，可以选择输出较大的f值;

③当ΔS和ΔS'属于模糊集MP或者LP时，表明群目标整体处于强机动，此时扩展状态的预测值可信度较小，量测修正的作用在增加.表1选择模糊集EP，选择输出较小的f值;

④当ΔS和ΔS'属于其他情况时，表明群目标整体处于弱机动，此时f的值应选择适中，因此表1中其余项选择模糊集MP、LP和VP.

f的隶属度函数如图2所示.

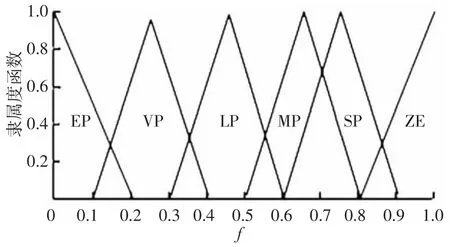
图2 f的隶属度函数

4)输出参数解模糊

采用重心解模糊法得到f的精确值

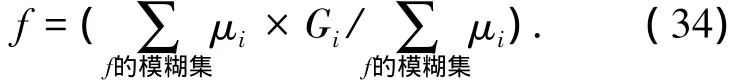
式中:μi为图2中对应f模糊集的隶属度，Gi则为各个模糊集的重心．

2.4 群分裂/合并机动的判定

通过对群运动的分析可知，当群分裂成不同子群时，群的扩展状态Xk出现异常情况，如群整体的椭圆面积发生很大改变，而此时即便增大质心滤波中的过程噪声方差Q，也无法有效预测群的运动行为．

主要采用Xk|k对应着的扩展椭圆的面积Sk=进行判断(d=2)．为了降低估计误差的影响，设计分裂/合并机动的判断步骤如下:

首先，根据滑动窗长度为N的扩展椭圆的面积积累值计算得到平均值:

然后，计算当前时刻扩展椭圆的面积的变化量:

最后，如果从k时刻起连续t个采样时刻内，都有，则判断此时出现分裂机动．如果连续t个采样时刻都有，则判断此时出现合并机动．其中，t和的具体取值视实际情况而定．一旦判定分裂或合并，就要增加或删除相应的群目标航迹．

3 仿真实验

3.1 群目标转弯场景

为了对比本文算法与文献［3］、［10］算法的性能，设置了二维空间内由5个目标构成的群目标的运动场景.群内目标并排成直线，彼此互相间隔500 m进行编队.传感器的扫描间隔T=10 s，其中在x轴和y轴的量测误差的标准差分别为σx=300 m和σy=100 m.为了简化传感器分辨率模型，假设每个目标的探测概率Pd=80%.群目标飞行总时长为65T，开始以v=300 m/s进行匀速飞行，在第10T～42T和52T～54T内分别依次执行一个360°和一个45°．的匀速转弯运动(径向加速度分别为0.5 g和1 g).文献［3］、［10］按照原文设置，采用的是Singer模型，本文使用的是MCS模型，其中机动频率都设置为α=0.1．扩展状态的自由度初始值a1=50，扩展状态变化率τ=5T．运行M=50次Monte Carlo仿真，本文提出的自适应跟踪算法与文献［3］、［10］算法进行比较，3种算法的群质心位置、速度和扩展状态的均方根误差(RMSE)如图3～5所示，其中RMSE的计算公式见文献［10］.

图3 群质心位置均方根误差

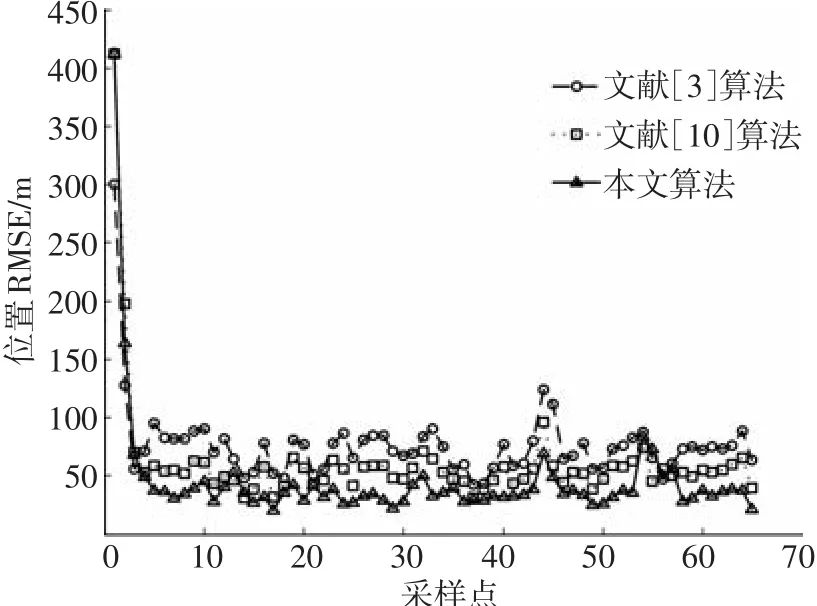
图4 群质心速度均方根误差

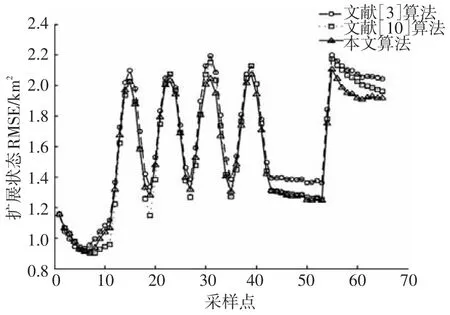
图5 扩展状态均方根误差

由图3、4可知，本文算法通过采用MCS模型，利用速度预测值和估计值的偏差来修正过程噪声方差，并根据量测残差大小实时调整渐消因子大小，从而自适应调整群质心的状态协方差的更新，尤其当群目标发生突然机动时(如仿真中的采样点42T和53T)，本文算法能够自适应调整有关滤波参数，降低算法估计的均方根误差.与文献［3］、［10］算法的整体估计结果对比，本文估计的群质心位置和速度的均方根误差更小，估计的精度更优.

由图5可知，在估计的前段，由于缺乏扩展状态预测的先验信息，估计精度要略低于文献［10］算法，但要高于文献［3］算法.而随着算法运行的逐渐稳定，估计精度要逐渐优于文献［10］，尤其是当群整体形状发生突然改变时，本文算法对扩展状态估计的自适应调整明显更快，具有更优的估计精度.

3.2 群目标分裂机动场景

参照文献［9］的仿真实验，本文设置了一个群目标的分裂机动场景，仍然沿用上一仿真实验的目标参数设置.群内目标并排成直线，彼此互相间隔500 m进行编队.群目标飞行总时长为30T，开始以匀速v=300 m/s进行飞行，在10T～15T内执行一个90°的匀速转弯运动(径向加速度为1 g)，最后在24T～30T执行分裂机动．

图6 群目标跟踪场景

图6(a)展示了群目标的量测数据，图6(b)展示了运用本文算法对群目标的跟踪效果图，其中*号代表质心的估计位置，椭圆代表群的扩展状态的估计结果.从图6中可知，当群目标在直线飞行时，可以较准确地估计群质心和扩展状态，当发生转弯机动时，估计误差会出现增大的情况，但是本文算法能够对跟踪结果迅速进行自适应调整.当群目标在执行分裂机动时，此时估计的扩展状态的椭圆面积迅速增大，并且此时扩展状态的估计效果受量测丢失情况的影响很大.通过上述结果可知，本文算法的跟踪结果可以较好反映出群目标的分裂机动情况.图7是滑动窗长度设置为N=3时，采用分裂判定方法的输出结果.

从图7中可以直观发现，在跟踪过程中，输出结果有两个增长的采样区间，分别对应着群目标的转弯机动和分裂机动.不同之处在于，前者增长的持续采样区间和变化幅度都远小于后者，因此容易通过设置合理门限，检测出群目标的分裂机动.

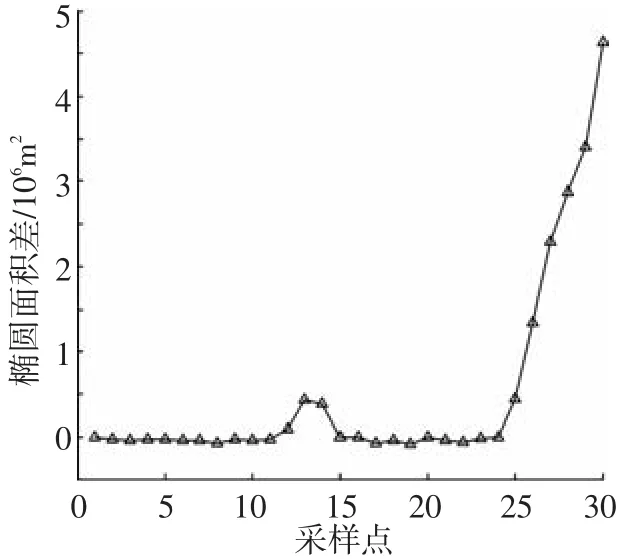
图7 分裂判定算法的输出结果

4 结语

本文提出了一种改进的群目标自适应跟踪算法，该算法利用群质心的速度预测值和估计值的偏差和输入残差大小，自适应调整群质心的过程噪声方差和质心状态协方差估计，提高了群质心在机动或者弱机动情况下的跟踪精度.在扩展状态估计中，将扩展状态对应的椭圆面积预测值和估计值的偏差及其变化率作为输入参数，利用模糊推理方法自适应输出扩展状态的预测值，提高了算法对群扩展状态在发生突发机动时的跟踪精度.另外通过分析群目标的分裂原理，设置了分裂机动的判决方法.仿真结果表明本文算法对群目标具有较好的自适应跟踪能力，并且能有效检测出群的分裂机动.

［1］BAR-SHALOM Y，LI X R.Estimation and tracking:principles，techniques，and software ［M］.Boston，MA:Artech House，1993.

［2］WAXMANN M J，DRUMMOND O E.A bibliography of cluster(group)tracking［C］//Proceedings of the SPIE International Conference on Signal and Data Processing of Small Targets.Orlando，USA:SPIE，2004:551-560.

［3］KOCH W.Bayesian approach to extended object and cluster tracking using random matrices ［J］.IEEE Transactions on Aerospace and Electronic Systems，2008，44(3):1042-1059.

［4］MAHLER R.PHD filters of higher order in target number［J］.IEEE Transactions on Aerospace and Electronic Systems，2007，43(4):1523-1543.

［5］GRANSTRÖM K，ORGUNER U.A PHD filter for tracking multiple extended targets using random matrices［J］.IEEE Transactions on Signal Processing，2012，60(11):5657-5671.

［6］连峰，韩崇昭，刘伟峰，等.基于SMC-PHDF的部分可分辨的群目标跟踪算法［J］.自动化学报，2010，36(5):731-741.

［7］FELDMANN M，FRANKEN D.Tracking of extended objects and group targets using random matrices-a new approach［C］//Proceedings of the 11th IEEE International Conference on Information Fusion.Cologne，Germany:IEEE，2008:1-8.

［8］FELDMANN M，FRANKEN D.Advances on tracking of extended object sand group targets using random matrices［C］//Proceedings of the 12th IEEE International Conference on Information Fusion.Washington，USA:IEEE，2009:1029-1036.

［9］FELDMANN M，FRANKEN D，KOCH W.Tracking of extended objectsand group targetsusing random matrices［J］.IEEE Transactions on Signal Processing，2011，59(4):1409-1420.

［10］UMUT ORGUNER.A variational measurement update for extended target tracking with random matrices［J］.IEEE Transactions on Signal Processing，2012，60(7):3827-3834.

［11］FELDMANN M，KOCH W.Comments on“bayesian approach to extended object and cluster tracking using random matrices”［J］.IEEE Transactions on Aerospace and Electronic Systems，2012，48(2):1687-1693.

［12］LI X R，JILKOV V P.Survey of maneuvering target tracking-Part1: dynamic models ［J］. IEEE Transactions on Aerospace and Electronic Systems，2003，39(4):1333-1364.

［13］潘平俊，冯新喜.基于强跟踪滤波器的自适应常加速模型及跟踪算法［J］.系统工程理论与实践，2008(5):136-141.

［14］LEI Y，LEI Y.Technique for target recognition based on intuitionistic fuzzy reasoning ［J］.IET Signal Processing，2012，6(3):255-263.

［15］CHAN K C C，VIKA L.Radar tracking for air surveillance in a stressful environment using a fuzzygain filter［J］.IEEE Transactions on Fuzzy Systems，1997，5(1):80-89.