基于锁相环的永磁同步电机无位置传感器控制技术研究

张泽宇，朱磊，张启平，汪伟

（武汉船用电力推进装置研究所，武汉 430064）

0 引言

永磁同步电机在现代交流调速系统中的应用越来越广泛，它具有体积小、重量轻、效率高、转矩脉动小等优点。永磁同步电机需要精确的转子位置角来实现闭环矢量控制，传统的方法是通过旋转变压器或者光电编码器等机械传感器实时检测，存在需要维护、可靠性差等问题。为克服机械传感器的缺陷，许多学者提出了无位置传感器控制方法。

无位置传感器控制按应用的转速范围来分，可分为低速和高速方法。高速如反电势积分法、扩展卡尔曼滤波、滑模观测器等观测方法，都基于电机反电势。当电机运行于低速区域或者零速时[1]，电机反电势很小，性噪比差，因此无法有效检测出转子位置。有学者提出适用于低速及检测电机初始位置的方法，这类方法基本思想是通过向电机定子端注入高频电压，检测出相应的高频响应电流，通过对其进行解算得到电机的转子位置角。这类方法主要包含高频旋转电压注入[2]和高频脉振电压注入两种方法。高频电压注入法仅适于具有一定的凸极性的永磁同步电机，对于隐极式PMSM不适用，这种方法易于实现，参数调节方便，由于利用了与电机转速无关的结构上的凸极效应，因此具有强鲁棒性。本文以低速凸极式PMSM为研究对象，研究了高频旋转电压注入的转子位置自检测方法，系统采用锁相环（Phase Lock Loop， PLL）作为转子位置观测器。最后本文给出了Matlab/Simulink下的仿真结果。

1 高频旋转电压注入法

1.1 高频激励下PMSM数学模型

在 αβ静止坐标系下注入旋转电压信号如下式所示：

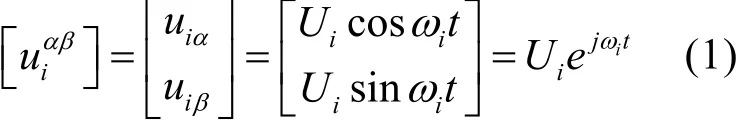
式中：iU为注入电压信号幅值，iω为注入电压信号角频率。

当注入的高频电压信号的频率远远大于永磁同步电机转速对应的频率时，可以忽略电机电阻压降和旋转电势，电机模型可简化为一个电感负载。在高频电压激励下永磁同步电机的模型可表示为：

dq为交直轴电感的对角矩阵，θr为转子的电位置角。

对式（2）积分可得αβ坐标系下高频响应电流为：

式中：Lavg为平均电感，Ldif为半差电感。

式（3）表明在电机中注入高频旋转电压后，定子电流响应中包含两个高频电流响应分量，其中第一项与注入高频电压同向同速旋转，称为高频响应正序电流iip，第二项与注入高频电压反向同速旋转，称为高频响应负序电流分量ini。可以看到仅负序分量包含转子位置角rθ，因此可以对该高频负序电流进行解算得到转子位置信息。

图1 滤波流程图

1.2 滤波环节

要获得高频负序电流，需要对采样电流进行滤波，滤掉与转子位置检测无关的信号，包括基波、低次谐波、高频正序电流、PWM开关谐波。传统滤波方法采用带通滤波器滤除基波以及PWM 开关谐波电流，采用同步轴系高通滤波器滤除高频正序电流[3]，BPF会引入相位滞后，导致观测的转子位置存在静差。本文首先采用同步轴系高通滤波器将高频正序电流滤除，然后将电流变换到估计的ˆdˆq旋转坐标系下，基波电流变为直流，同样利用 HPF滤除。经过两级HPF滤波后电流中包含负序电流以及其他谐波噪声，通过一个旋转坐标变换将负序电流化为直流，利用低通滤波器滤除谐波，滤波后通过旋转坐标变换，使电流中不含注入频率iω。由于LPF对于直流量不存在相移，因此滤波过程不会引入相位滞后。完整的滤波流程如图1所示。两个HPF以及LPF均设计为一阶，截止频率都取10 Hz。

1.3 锁相环转子位置观测器

滤波后的负序电流为转子位置角函数的旋转电流矢量，通过外差法构造转子位置角误差，通过锁相环调节位置角误差为零，使观测位置角ˆrθ跟踪电机转子位置角rθ，从而提取出转子位置角。控制框图如图2所示。

图2 采用外差法的PLL转子位置跟踪观测器

锁相环主要由鉴相器（Phase Detector， PD）、环路滤波器（Loop Filter， LP）和压控振荡器（Voltage Controlled Oscillator， VCO）三个基本单元组成。压控振荡器输出跟踪得到的相位信号，鉴相器实现输入信号相位与跟踪相位的比较，其输出送入环路滤波器，环路滤波器输出一个电压信号给压控振荡器，该信号控制压控振荡器输入信号频率跟踪输出信号频率，当两者频率相等时，鉴相器输出信号跟踪输入信号相位实现锁相，两信号存在一个稳定的相位差。对于PMSM调速系统，当VCO输入频率跟踪电机转速对应频率时，这时观测得到的转子位置角逼近实际值。环路滤波器由一阶LPF和PI调节器构成，LPF滤除系统噪声，PI调节器调节PLL输出信号相位实现相位跟踪。

外差环节可以看作PLL鉴相器，由其构造的转子位置角误差为：

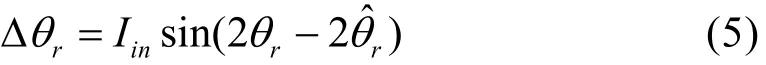
式中inI为负序电流的幅值。

当转子位置角误差很小时，在其工作点附近线性化以后，转子位置角误差表示为：

锁相环闭环传递函数为：

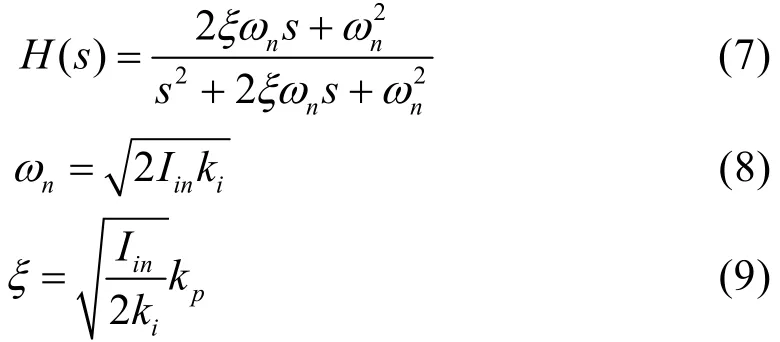
式中：ωn为无阻尼振荡角频率，ξ为阻尼比。

锁相环要保持相位跟踪要满足以下两个条件，这就决定了锁相环参数设计范围。

1）锁相环输入端给定阶跃信号的最大频率必须小于失步带宽1.8ωn( ξ +1)[4]。

观测转速可取PI调节器输出信号或者I调节器输出信号。对于前者而言，比例调节器会放大系统干扰与噪声，脉动较大，不能直接用于矢量控制系统的速度闭环，因此采用后者作为电机观测转速。

2 仿真验证

为验证高频注入法的可行性，本文采用一台凸极式永磁同步电机参数在 Matlab/Simulink上进行了仿真，仿真参数如表1所示。

表1 仿真参数

经过滤波以后送入PLL的高频负序电流波形如下图所示。

图3 高频负序电流

图4 转速观测值与实际值

图4、5给出了转速观测值、实际值及观测误差值。电机观测转速在调速过程中存在误差，平均为2.5 r/min，最大为3.3 r/min；在稳态情况下，电机转速存在±0.2 r/min的脉动，误差平均值几乎为零。图6、7给出了转子位置观测值、实际值及观测误差值，转子位置观测误差在电机启动时，误差范围为1.5°～11.3°，误差平均值在6°左右，稳态时误差范围为-3°～2.8°，误差平均值几乎为零。采用高频注入法PMSM能平稳的加速到给定转速，具有较好的动、静态性能。

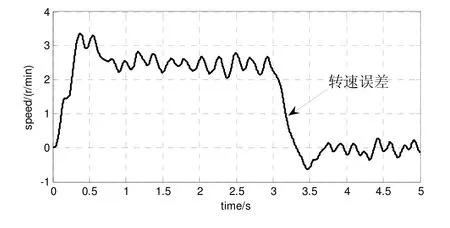
图5 观测转速误差

图6 转子位置观测值与实际值

图7 转子位置观测误差

3 结论

本文在建立高频电压注入下永磁同步电机的数学模型的基础上，对无位置传感器控制方法进行了仿真。仿真结果表明，利用一阶高通和低通滤波器能获得较好的滤波效果，滤波后的高频负序分量较平滑；电机在调速过程中能较为平稳的上升到给定转速，转子观测误差在系统可以接受的范围内，因此基于转子锁相环的高频电压注入法，可以应用于凸极式PMSM无位置传感器矢量控制系统中，并能获得较好的动、静态特性。

[1]郑泽东, 李永东.永磁同步电机控制系统综述. 伺服控制. 2009（1）: 22,24-26.

[2]Jansen P L, Lorenz R D. Transducerless Position and Velocity Estimation in Induction and Salient AC Machines. IEEE Transactions on Industry Applications,1995, 31 (2) : 240～247

[3]刘毅, 贺益康, 秦峰, 贾洪平. 基于转子凸极跟踪的无位置传感器永磁同步电机矢量控制研究. 中国电机工程学报, 2005, 25（17）:121-126.

[4]Floyd M.Gardner著. 锁相环技术（第三版）. 北京:人民邮电出版社, 2007.