磁悬浮储能飞轮用径向磁轴承磁路仿真分析

李泽辉，滕万庆，李 翀

（哈尔滨工程大学储能技术与应用研究所，黑龙江 哈尔滨 150001）

飞轮储能是将高速旋转飞轮的机械能转换为所需能量的一种具有广泛应用范围的新型储能技术。相对其它储能技术，其具有高转化率、无污染、低噪声、维护简便、安装面积小等优点，在汽车、船舶、航天、电网等领域都有广泛的应用。磁悬浮轴承是飞轮储能关键组成之一，其利用电磁力作用将转子悬浮于空间，使转子与定子之间没有机械摩擦，是一种新型、高性能轴承。在实现高转速的同时，还具有无机械磨损、能耗低、噪声小、寿命长、无需润滑、无油污染等优点，磁悬浮轴承性能的好坏，直接影响飞轮储能设备储能转化效率的高低。目前，哈尔滨工业大学、浙江大学、北京航空航天大学、南京航空航天大学、哈尔滨工程大学等国内多所高校开展了磁悬浮轴承领域相关技术的研究工作。

对磁悬浮轴承而言，其关键技术之一就是磁路分析，它是磁悬浮轴承设计与计算的基础，磁悬浮轴承磁支撑性能的好坏与它的磁场设计息息相关。在对磁悬浮轴承进行结构设计和优化时，一般将磁场简化为磁路，通过忽略漏磁、设定磁势全部作用在工作气息中的理想条件下，进行理论分析并得出计算结果，这已经成为许多电磁计算程序的固定模式。但是，上述方法对于铁磁材料非线性磁化特性、漏磁效应及数据计算的准确性等却无能为力，也无法给出磁场的分布状态，必然导致对磁力轴承的特性和结构参数分析不够全面，而且即使磁路计算比较准确，也并不一定能解决所有的问题。因此，采用更为准确的场论分析方法对深入研究磁力轴承的特性很有必要[1-2]。根据ANSYS仿真计算获取磁轴承磁场参数及分布数据，验证理论计算参数，察看磁悬浮轴承设计是否合理，是否有磁感应强度过饱和的地方，降低样机二次加工的概率，减少研发时间，从而为磁悬浮轴承样机的研制和优化提供支持[3]。

1 径向磁悬浮轴承电磁场的分析过程

应用ANSYS有限元分析软件，以八极定子的径向磁轴承为分析对象，其主要设计参数为：定子的内径φ=60.6 mm，外径φ=150 mm，转子直径φ=60 mm，磁极气隙0.3 mm，一对磁极（两个磁极）上的线圈匝数为144匝，磁轴承轴向长度45 mm（有效导磁长度为43.73 mm），磁极宽度12 mm，槽满率0.7，最大磁感应强度为1.2 T，最大支撑力为500 N，结构示意图如图1所示。

图1 八极径向磁轴承结构示意图 Fig.1 The octupole radial magnetic bearing structure diagram

1.1 几何建模

对磁轴承几何建模可以在ANSYS环境下实体建模或直接建立模型，也可以通过其自带接口从其它软件（如CAD、UG等）导入，一般多应用实体建模。径向磁轴承建立有限元模型包含五个部分：定子、转子、线圈、转轴及空气层。在径向磁轴承中转子高速旋转（本设计转速约为1.5×104r/min），磁通量只通过转子上的叠层硅钢片，因此转子端部的影响可以忽略；当分析磁轴承的实际工作点时，由于其高速旋转，可忽略定子中转轴部分的磁通量，可以将实心转轴建模为空气[4]。在本设计中，磁力轴承控制电流的频率和幅值比偏磁电流小得多，可近似看作恒定直流。对于磁力轴承电磁场而言，由于本次研究的主要目的是分析与时间没有关系的磁场特性，为了简化计算，将磁力轴承电磁场近似为静态场来分析，建立二维模型，如图2所示。

图2 八极径向磁轴承几何建模 Fig.2 The octupole radial magnetic bearing geometric modeling

1.2 选择单元类型、定义材料性能

建立二维模型可选用二维静态电磁场分析实体单元PLANE13或PLANE53进行求解，单元类型号为1，选择磁矢势Az这一自由度，远端空气可用无限单元IFIFIN110进行划分。如果建立三维模型可选用三维静态电磁场分析实体单元 SOLID98或SOLID117进行求解，远端空气可用无限单元IFIFIN47进行划分[5]。

定义空气的相对磁导率为1.0，材料编号为1；定子采用叠层硅钢片为材料，可输入BH曲线或相对磁导率，材料编号为2；转子采用电工纯铁DT4为材料，可输入BH曲线或相对磁导率，材料编号为3；芯轴采用45号钢为材料，输入相对磁导率为1.0，材料编号为4；线圈采用直径为1.38 mm的漆包线，定义线圈的相对磁导率为1.0，材料编号为5。

1.3 设置网格密度并划分网格

对模型进行网格划分，设置网格形状和大小。注意设置适当的网格密度，太大容易导致计算结果不收敛，太小容易导致计算量加大，计算速度慢。在这里采用智能网格划分，设定智能网格划分的等级为4。

1.4 加载和指定边界条件

在施加边界条件和载荷时，既可以给实体模型（关键点、线、面）也可以给有限元模型（节点和单元）施加边界条件和载荷。包括：确定矢量磁势边界条件，分析类型，线圈以及激励频率等。本例以定子外圆为边界，设定边界条件为零磁势，令磁力轴承对于定子以外区域没有漏磁，整个磁场限定在定子内部，加载线圈的电流密度[6]。

1.5 求解

运用单元工具获得积分点，建立求解所需的矩阵；用求解器对已建立好的方程求解，获得基本解；通过单元的形函数以及其它一些工具获得单元的导出解。具体步骤为：定义分析类型，定义分析类型选项，备份数据库，开始求解，收敛图形跟踪，完成求解。

1.6 察看结果（后处理）

求解结束后，利用 ANSYS的两个后处理器POST1或POST26查看计算结果，包括磁力线、等值线、矢量显示、表格显示、磁力、力矩、线圈电阻及电感等[7-10]。

2 仿真结果分析

2.1 分析是否存在漏磁、电磁耦合

原始电磁力的计算公式为

式中，B为铁磁材料磁感应强度，S为有效磁极面积，0μ为真空磁导率，∂为修正系数，δ为气隙长度。当设计对象磁通分布均匀、工作气隙较小（＜0.3 mm）的情况下，可忽略漏磁及磁通分布不均对电磁力的影响，简化计算，即修正系数为 0。本文设计的径向磁轴承，稳态单边工作气隙为 0.3 mm，除磁轴承定子及磁轴承转子为导磁材料外，其它材料均为非导磁材料，因而符合上述要求。

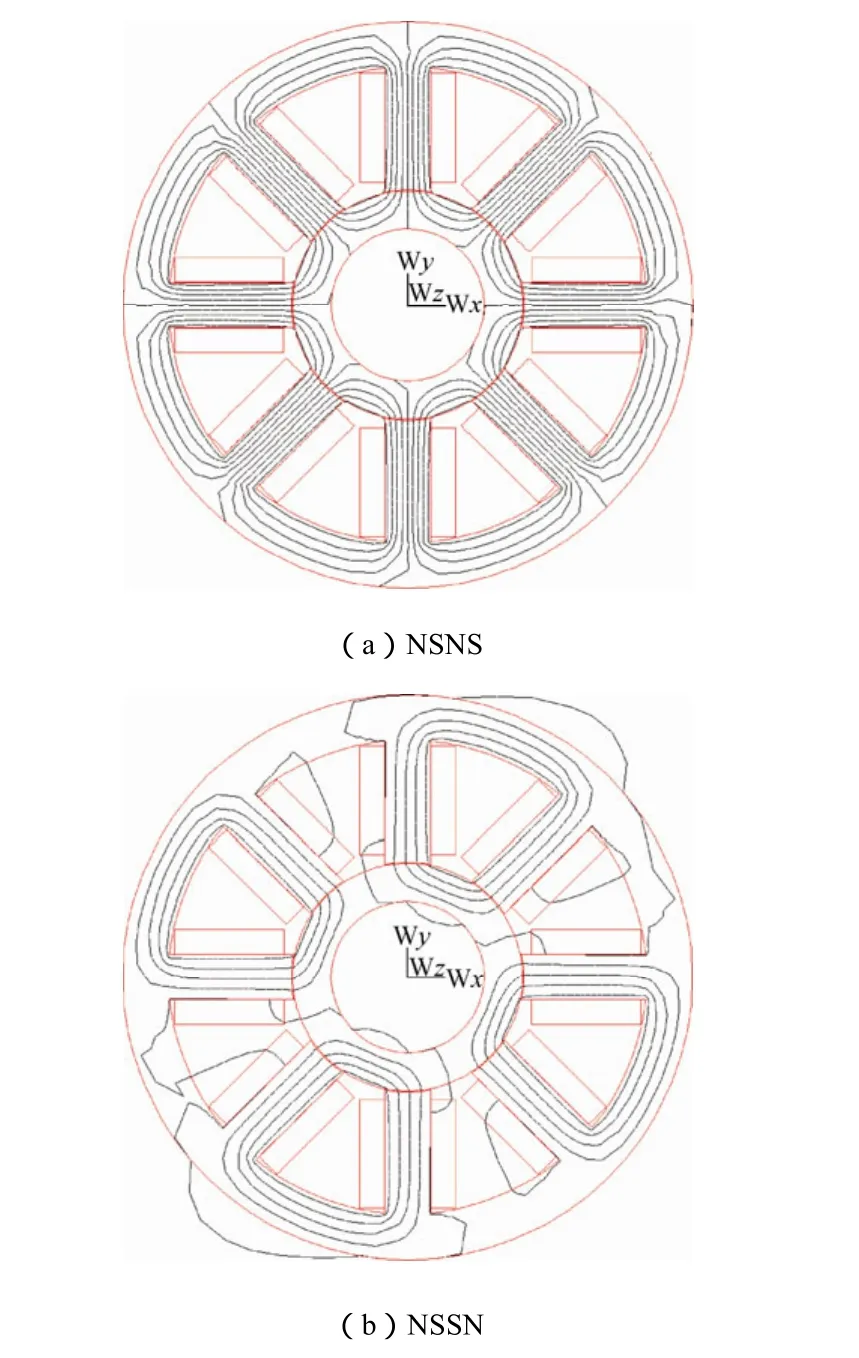
图3 径向磁轴承磁力线分布图 Fig.3 Radial distribution of the magnetic field lines of magnetic bearings

图3(a)和图 3(b)清楚地表示出径向磁轴承在 NSNS和NSSN两种磁极布置形式下的磁力线分布情况：① 相比NSSN磁极布置方式，NSNS磁极布置方式各相邻磁极间耦合现象明显；② 虽然NSSN磁极布置方式存在磁泄露，即向线圈中泄露，通过定子向空气中泄露和通过定子向转子中泄露，但通过图3(b)可知泄露都很小，可以忽略，后面电磁力的仿真结果也验证了这一结论。

2.2 察看是否存在磁感应材料过饱和的情况

由式(1)可以看出，磁极面积固定时，磁感应强度与电磁力成正比关系，但当铁磁材料的磁感应强度达到最大值时，再继续增加电流是不会增加电磁力的，因此要保证电磁轴承在达到最大承载力时对应的磁感应强度没有达到材料的最大磁感应强度。

图4(a)和图4(b)清楚地表示出径向磁轴承在NSNS和 NSSN两种磁极布置形式下的磁通密度分布情况：①相比NSSN磁极布置方式，NSNS磁极布置方式各相邻磁极上磁感应强度要相对大一些；②虽然NSSN磁极布置方式各相邻磁极上磁感应强度要相 对大一些，但也没有达到过饱和程度，说明结构磁轴承结构设计合理，不存在过饱和磁感应强度的问题。

图4 径向磁轴承磁感应强度矢量图 Fig.4 Radial magnetic bearing magnetic induction vector

2.3 计算电磁力

将轴承设计参数代入式(1)得到最大电磁力500 N，ANSYS仿真电磁力为455 N，误差为9%，通过计算结果验证，结构设计合理，符合设计预期，为后续磁悬浮轴承样机的研制提供了数据参考。

3 结 论

文中给出了应用ANSYS有限元软件进行电磁场分析的全部过程。以径向磁轴承为载体进行仿真计算，通过计算结果可以看出：①有限元软件可以快速方便的对磁轴承进行建模并获取所需的试验数据；②验证了理论计算的正确性；③NSSN磁极布置方式相比NSNS磁极布置方式更为合理；④虽然实验数据显示实例径向磁轴承在空气及主轴中存在漏磁，相邻磁极间存在磁场耦合等现象，但都在可接受范围内，电磁支撑力计算数据与设计数据间误差为 9%，符合设计要求，径向磁轴承结构设计合理；⑤以上数据为理论计算提供了参考反馈数据，降低样机二次加工的概率，缩短研发时间，从而为磁悬浮储能飞轮的顺利研发提供了必要的支持。

[1] Zhang Chaoping（张超平），Dai Xingjian（戴兴建），Meng xiangyong（孟祥泳），et al.Online balancing of the rotor-bearing unit of the flywheel energy storage system[J].Energy Storage Science and Technology（储能科学与技术），2013，2（3）：181-184.

[2] Wen Xianglong（文湘隆），Hu Yefa（胡业发），Ding Guoping（丁国平），Chen Long（陈龙）.The study of the effects of locating groove on the radial active magnetic bearing[J].Machine Tool &Hydraulics（机床与液压），2006，（3）：32-33.

[3] Zheng Jianqiang（郑坚强）.The analysis, structural design and control of magnetic Bearing finite element[D].Hangzhou：Zhejiang University，2004.

[4] Hsiao F Z，Lee A C.An investigation of the characteristic of electromagnetic bearing using the finite element method[J].Journal of Tribology，1994，116：710-719.

[5] Wen Xianglong（文湘隆），Hu Yefa（胡业发），Ding Guoping（丁国平）.基于 ANSYS的径向磁力轴承电磁场分析[J].Machinery（机械制造），2006，（8）：42-43.

[6] Chen Diyi（陈帝伊）.The electromagnetic field analysis and structural optimization design of radial magnetic bearing[D].Jinan：Shandong University，2008.

[7] Han Bangcheng（韩邦成），Li Yefan（李也凡），Jia Hongguang（贾宏光），Wu Yihui（吴一辉）.Calculation of forces of radial active magnetic bearing using finite element method[J].Tribology（摩擦学学报），2004，24（3）：160-163.

[8] Tang Xinglun（唐兴伦），Fan Qunbo（范群波），Zhang Zhaohui（张朝晖），Li Chunyang（李春阳）.ANSYS 工程应用教程——热与电磁学[M].Beijing：China Railway Publishing House，2003.

[9] Zhang Qian（张倩），Hu Renxi（胡仁喜），Kang Shiting（康士廷）.ANSYS12.0电磁学有限元分析从入门到精通[M].Beijing：China Machine Press，2010.

[10] Zhang Wei（张伟），Wang Weixin（王维新）.Analysis of 3D finite element based on magnetic radial bearing[J].Modern Electronics Technique（现代电子技术），2009，24（12）：93-99.