菲涅耳双棱镜干涉实验的误差改进

姚雪 都进学 王全武

(重庆科技学院数理学院，重庆 401331)

利用光的干涉、衍射原理进行光波波长测量实验时，通常误差较小，一般能控制在3%以内。目前菲涅尔双棱镜干涉测钠黄光的波长实验实验误差却偏大，一般只能控制在5%以内。本次研究目的是提高测量精度，降低实验误差，改该实验效果。

1 菲涅耳双棱镜干涉实验测波长原理

菲涅耳双棱镜干涉实验测波长作为大学物理的基本光学实验之一，简单易懂，实验现象良好。菲涅耳双棱镜干涉实验是利用双棱镜界面的两次折射，将单缝s发生的光波阵面分成沿不同方向传播的两束光，这两束光相当于由虚光源s1、s2发生的两束相干光，在它们相重叠的空间区域内产生干涉。该区域中均可得到明暗交替的干涉条纹。实验原理如图1所示。

图1 菲涅耳双棱镜干涉实验原理图

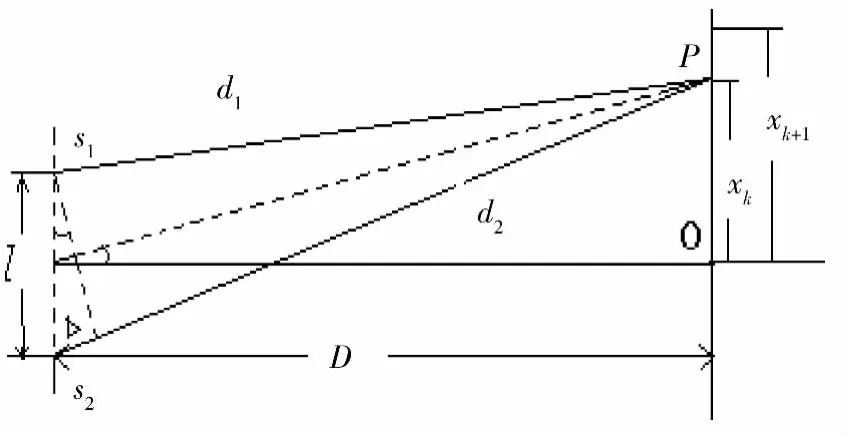
图2 菲涅耳双棱镜干涉实验简化光路图

根据干涉理论Δ=Kλ，为亮条纹，因此可推得亮条纹位置满足以下关系:

暗条纹位置则满足关系:

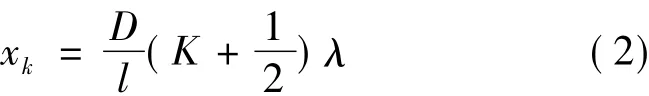
由式(1)、(2)可看出，任何两条相邻的亮条纹(或暗条纹)之间的距离即干涉条纹间距为:

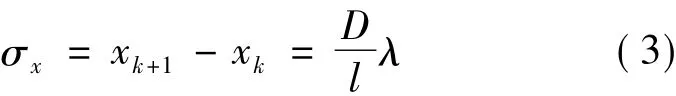
所以计算光波波长的原理公式为:

只需要测出l、D和σx，就能根据式(4)来计算光波波长。

2 菲涅耳双棱镜干涉实验测波长的不足

计算光波波长的原理公式非常经典，简单可测。大多数高校在该实验中采用一次成像法计算l，平值法测σx，对D采用了近似相等的取值，无疑增大了系统误差。

(1)D采用近似间接测法。以狭缝平面代替虚光源平面，以狭缝底座上的标线代替狭缝平面位置，用狭缝平面与观察屏的距离代替D。这种近似方法存在狭缝与虚光源并不共面的系统误差。即使D自身足够大时，狭缝平面与虚光源平面相差很小，所含系统误差可忽略。但狭缝与其底座上的标线也不共面。另外观察屏位置无法直接测量，具体计算D时，用狭缝平面与目镜距离减去厂家所设目镜到观察屏距离，进行间接计算，同样会增大其系统误差。

(2)l的数值一般采用一次成像法计算。即保持狭缝、双棱镜和测微目镜位置不动，在双棱镜和观察屏之间放上透镜L，调节L使得在读数显微镜中出现清晰的像 s′1、s′2，记下缝、双棱镜、透镜 L 以及测微目镜的位置。测出 s′1、s′2之间的距离 l′。根据透镜成像光路得，故只要求出 a、b 值，读数显微镜测出l′，就可算出l。此方法简单，但同样用狭缝到透镜距离代替物距a，使a、b的值仍然存在较大的近似性，导致l的测量出现误差。

(3)测量干涉条纹间距σx，采取连续读出8σx或者10σx的宽度，然后求出平均值的方法计算。满足D＞4f时，干涉条纹清晰可见，但光强原因导致亮度较暗，在连续数多条条纹间距时非常容易出错，会导致较大的系统误差。

3 实验优化措施

针对以上产生误差的原因，通过大量翻阅资料并进行推算，找出减小误差的具体理论计算公式及相应的测量方法。

(1)两虚光源间的距离l以及虚光源到屏的距离D理论计算公式推导。图3所示为凸透镜二次成像的光路图，其中透镜处于I位置时成像物距为u1，像距为v1，处于Ⅱ位置时成像物距为u2，像距为v2，透镜焦距为f，透镜I、Ⅱ位置的距离为D1。下面利用二次成像推导的虚光源间距离l的计算公式。

图3 二次成像光路图

当透镜处于Ⅰ位置成像时，有:

根据空气中的高斯公式得:

当透镜处于位置Ⅱ成像时，有u2=D-v2，根据空气中的高斯公式可得二次成像时的焦距:

同一透镜焦距f相同，由式(5)、(6)可得

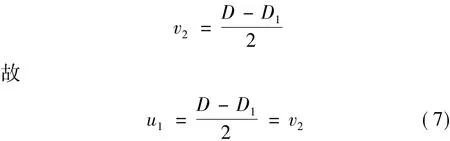
对于虚光源s1，结合式(7)，有

对于虚光源s2，有:

由式(8)、(9)两式相乘可得:

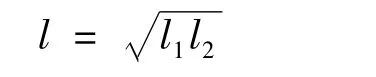
下面利用以上结论推导D确切计算公式

由式(8)、(9)两式相除可得:

结合式(7)(10)可得

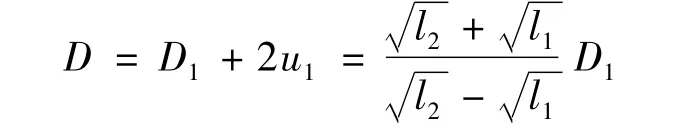
由此可见，采用二次成像法，只要测出 l1，l2，D1，便能较为准确地求出l和D。

3.2 逐差法计算σx

条纹间距为等间距，实验中都能调出15个左右的条纹间距。为了克服连续多个条纹间距容易数错的问题，我们可以采用逐差法计算以减小误差。具体做法是:克服回程差后，向着同一个方向每2个条纹读一次其位置坐标，连续读出6组数据，记为k1，k2，k3，…，k6。用逐差法计算:

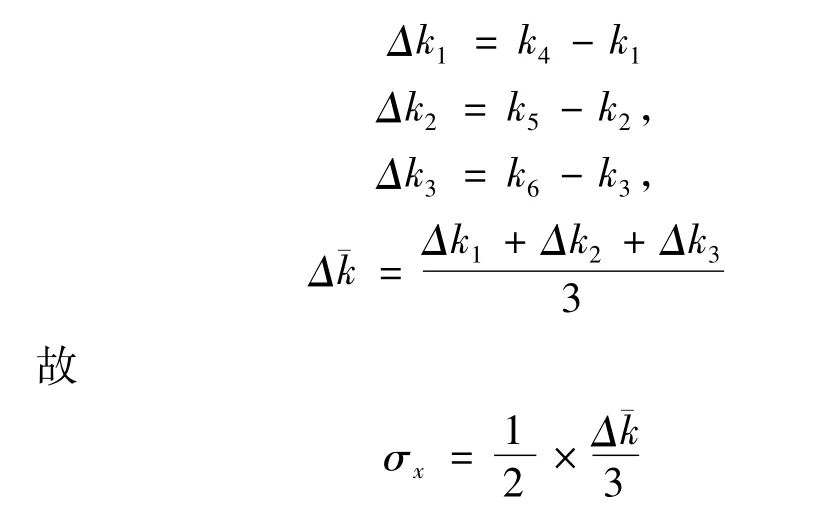
4 实验数据实例对比分析

当调试好满足条件的干涉条纹后，固定狭缝、双棱镜、测微目镜的位置分别分别为133.00、122.30、32.63 cm。二次成像的透镜位置分别为76.25、47.78 cm。虚光源间距离l以及条纹间距σx的测量数据分别如表1、表2、表3。

表1 二次成像法测量数据 mm

显然，根据改进前的计算方法，由表1、表2可得:

表3 逐差法测量条纹间距σx mm

根据改进后的推导公式及二次成像法，由表1、表3可得:

根据改进后的公式和方法多次进行测量，数据对比分析发现误差均较改进前小，并且改进后误差基本能控制在1%以内。由此可见，该方法对减小误差有一定的参考意义。

5 结论

(1)采用二次成像法，可直接用读数显微镜较准确地测量l1、l2，根据公式计算两虚光源间距离l，从而可提高l的精确度。

(3)多次读数，用逐差法计算σx，可有效降低读数误差。

将以上理论分析应用到实验当中，测出l、D和σx，代入原理公式计算出光波的波长。经多次测量，相对误差均可以控制在1%以内。

实验中，在二次成像法成放大像时测量像距，遇到了困难，像找不到。分析发现其原因，D大于4f虽然都能二次成像，但当D过大，会导致成放大像时两虚光源成像的距离l2过大，超出了读数显微镜的范围，不便测量。D过小，两次成像的透镜距离过小，不便测量，且增大了D1的误差。经过反复实验发现，D只略大于4f就行了。当透镜焦距等于190 mm时，狭缝和显微镜的距离为100～110 cm时效果较好，不会出现上述问题。

［1］葛松华，唐亚明.菲涅耳双棱镜干涉实验中虚光源位置的讨论［J］.大学物理实验，2011(2):56－57.

［2］唐海燕.大学物理实验［M］.北京:国防工业出版社，2010:192－196.

［3］洪丽.菲涅耳双棱镜干涉实验中凸透镜的成像［J］.海南师范学院学报，2007(1):48－49.