单相重合闸对抽水蓄能发电机组的寿命影响

2014-09-21李金香衣然王小鹏

大电机技术 2014年3期

关键词：机座单相重合

兰波，李金香，衣然，李博，王小鹏

（水力发电设备国家重点实验室，哈尔滨 150040）

单相重合闸对抽水蓄能发电机组的寿命影响

兰波，李金香，衣然，李博，王小鹏

（水力发电设备国家重点实验室，哈尔滨 150040）

电力系统运行表明，大多数故障是输电线路上发生的瞬时性短路故障，尤以单相接地短路故障居多，约占70%以上。为了提高电力系统的安全稳定运行能力，国内外普遍采用重合闸操作，其成功率高达60%～90%。重合闸操作会引起连续的电气暂态过程，给系统中各种设备如发电机、电动机等造成冲击，进而在其相应部件上产生疲劳损耗。疲劳损耗的累积超过相应部件的寿命，就会造成电机不同程度的疲劳损坏。因此，掌握事故工况下发电电动机的疲劳损耗影响对机组安全可靠影响有着非常重要的意义。

单相重合闸；FEM；疲劳损耗；抽水蓄能

0 前言

电力系统运行表明，大多数故障是输电线路上发生的瞬时性短路故障，尤以单相接地短路故障居多，约占70%以上。为了提高电力系统的安全稳定运行能力，国内外普遍采用重合闸操作，其成功率高达60%～90%。重合闸操作会引起连续的电气暂态过程，给系统中各种设备如发电机、电动机等造成冲击，进而在其相应部件上产生疲劳损耗。疲劳损耗的累积超过相应部件的寿命就会造成电机不同程度的疲劳损坏。因此，掌握事故工况下发电电动机的疲劳损耗影响对机组安全可靠运行有着非常重要的意义。

重合闸操作对汽轮发电机的影响，早在上世纪已开展了广泛的研究[1-3]。在最不利时间组合条件下，重合于高压出线出口附近的三相短路和两相接地短路，有可能一次性地耗尽汽轮发电机组轴系的疲劳寿命，并提出了大型电厂的高压出线端应禁用一般的三相快速重合闸操作，指出单相故障单相快速成功重合闸的疲劳损耗小于0.01%，不成功重合闸的疲劳损耗在0.01%～0.1%之间。而重合闸操作对水轮发电机以及抽水蓄能电机影响的研究还未见报道。因此有必要分析电力系统重合闸操作对抽水蓄能电机的影响。

本文针对抽水蓄能电机在发电和电动两种工况下单相重合闸过程进行机组的疲劳损耗分析。

1 单相重合闸原理及数学模型

1.1 重合闸过程概述

当输电线路上发生单相对地短路时，为保持发电机与电力系统或电力系统间的完整性和稳定性，一般只切除故障相，其余两相仍继续运行。若故障是暂时性的，单相切除后，故障点电弧经过一段时间后会自动熄灭，绝缘强度恢复，单相重合后，系统又恢复到原来的结构，这种情况是单相成功重合闸；若故障是永久性的，单相重合时故障依然存在，经过一段时间再行三相永久切除，这种情况是单相不成功重合闸。

当输电线路上发生两相相间短路，两相对地短路，三相短路故障时，故障线两端的断路器就会三相跳闸。若故障是暂时性的，经过一段时间后重合被切除的三相线路，系统又恢复了原来的结构，这种情况是三相成功重合闸；若故障是永久性的，三相重合后再进行三相永久切除，这种情况是三相不成功重合闸。

除单相、三相重合闸外，还有快速或延时重合闸、自动与手动重合闸、一次或多次重合闸。各种重合闸过程的共同之处就是故障发生、切除、重合，若不成功，再切除。故障发生的时刻是随机的，但故障发生到切除的时间是限定的，它是由继电器和断路器的动作时间决定的。这段时间称作切除时间。我国电网中的切除时间一般在0.07～0.1s之间。

1.2 数学模型

首先通过电磁场分析确定单相重合闸工况下随时间变化的电磁扭矩，作为有限元结构场分析的输入数据。通过有限元瞬态分析程序计算随时间变化的扭矩对发电机定子机座的影响。最后利用金属疲劳理论，对定子机座动态应力产生的疲劳损耗进行计算和安全评估。

（1）电磁场分析。采用SIMSEN软件对双机无穷大系统进行仿真，仿真模型[5,6]如图1所示，模型中包括无穷大系统（VSRES）、发电电动机（SM）、主变压器（TP）、输电线路（LNRES）、断路器（CBS）、接地点设置开关（CBG）、励磁调节器（VREG）、电机定子（STA）、转子（ROT）和水泵水轮机（TURB）的机械系统等。

（2）瞬态动力学分析。主要包括：运动方程、求解方法和积分时间步长确定。

用于瞬态动力分析的运动方程和通用运动方程相同，见式（1），这是瞬态分析的最一般形式，载荷可为时间的任意函数；

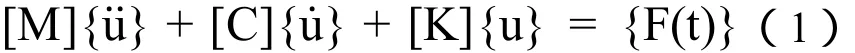
运动方程（1）有两种求解方法：模态叠加法和直接积分法。本文采用直接积分法对定子机座模型进行分析。其特点是运动方程可以直接对时间按步积分。在每个时间点，需求解一组联立的静态平衡方程（F=ma）；求解时使用完整结构矩阵，不进行缩减。积分时间步长（亦称为ITS 或Δt）是时间积分法中的重要概念，ITS应用于直接积分法中，必须足够小以精确捕捉下列数据：响应频率、载荷突变、接触频率（如果存在）。根据电磁计算，单相重合闸交变扭矩震荡一个周期的时间为0.02s，因此本文将电磁扭矩震荡一个周期分为8份，即采用0.0025s作为计算由于电磁扭矩引起的定子机座动态扭矩的积分步长。

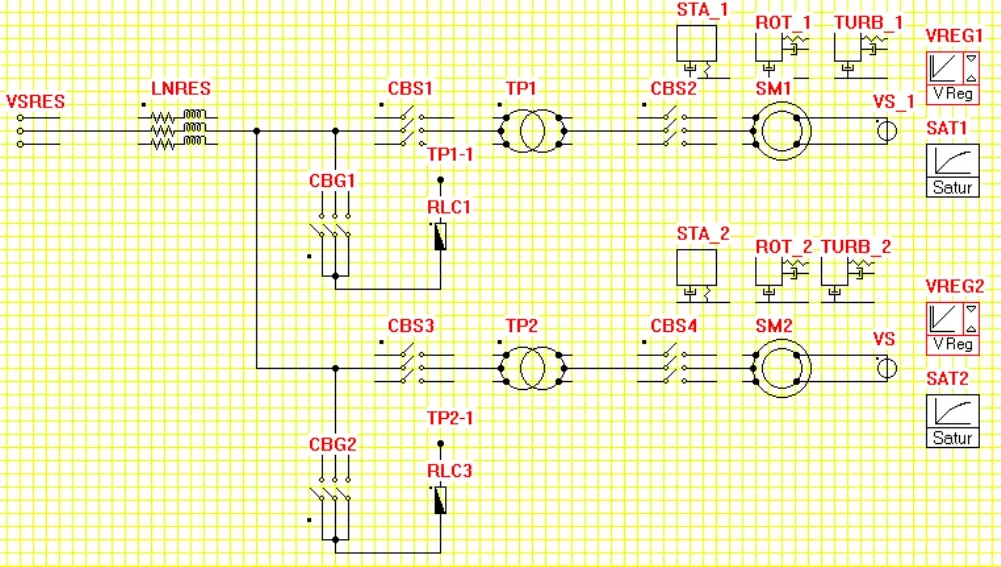
图1单相重合闸仿真模型

（3）疲劳分析。采用雨流法对动态应力和作用频率进行计数，采用线性米勒法计算疲劳损耗。

雨流计数法也叫塔顶计数法，其主要特点是根据研究材料的应力－应变过程进行计数，统计载荷波形中的循环和半循环。

雨流法计数方法如图2。

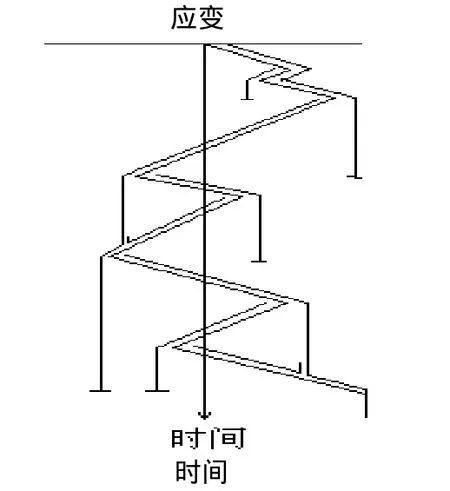
图2

（a）雨流的起点依次从每个峰值的内侧边开始，波形左半部为内侧边；

（b）雨点在下一个峰值落下，直到对面有一个比开始时的峰值更大的峰值为止，也就是说比开始时的最大值更大的值或者比最小值更小的值为止；

（c）当雨流遇到来自上面屋顶流下的雨时，也就停止；

（d）按以上过程取出所有全循环，并记下各自的变程；

（e）再按正负斜率去除所有半循环，并记下各自的变程；

（f）把取出的半循环按修正的“变程对”计数法配成全循环。

线性疲劳积累损伤准则考虑到发电电动机在单相重合闸工况下每个循环的应力幅分别为 Sa1、Sa2、Sa3……，对应的交变循环次数为nl、n2、n3……，（Sa1为单独作用时的疲劳寿命为N1，以此类推），认为Sa1作用了n1次，对结构所造成的损伤程度为n1／N1，其他应力幅所造成的损伤程度为n2／N2、n3／N3……。线性疲劳积累损伤准则认为各应力幅造成的损伤程度累计叠加不应超过1，即：

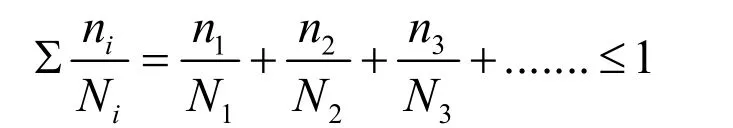
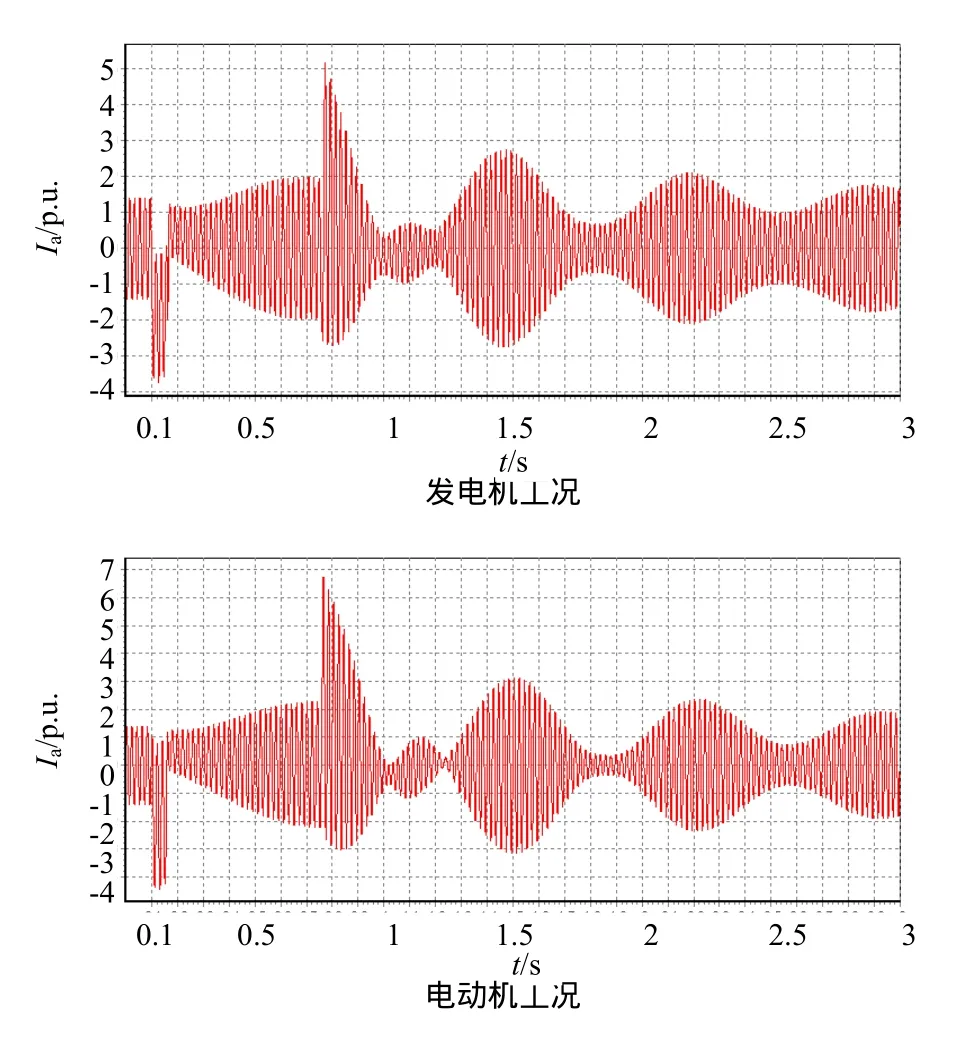
图3 A相成功重合闸，A相电流曲线

1.3 单相重合闸仿真结果

本文以某抽水蓄能电站300MW等级的抽水蓄能电机及其单回线输电线路为例，进行了发电和电动工况成功和不成功单相重合闸仿真分析。

单相接地短路点假定在主变高压侧出口，而不是线路的某个位置，原因是在不考虑线路阻抗的情况下电机的故障电流和电磁转矩最大，换句话说，此处短路对电机产生的冲击最大。另外，短路时刻对短路电流及电磁转矩都有影响。文中通过多次仿真确定了短路电流和电磁转矩最大时刻，在单相重合闸过程中短路时刻就是按此设定的。

图4 A相不成功重合闸，A相电流曲线

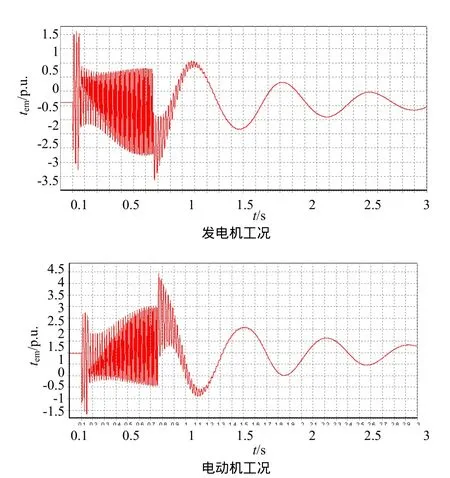
图5 A相成功重合闸的电磁转矩曲线

根据所研究电机的具体情况，单相重合闸过程设定为：主变高压侧线路A相在0.1s时单相对中性点接地，经过 0.02s检测时间及 0.04s跳闸时间，在0.16s时主变高压侧 A相断路器单相跳闸、再经过 0.6～1.5s短时缺相运行，即0.76～1.66s时重合闸。本文假定0.76s和1.66s两个时刻进行成功和不成功单相重合闸。若重合闸后故障仍然存在，再经过0.06s后，即在0.82s或1.72s时刻实施三相永久切除，即不成功单相重合闸。图3～6给出了发电和电动工况分别在0.76sA相成功和不成功重合闸电磁转矩和故障相电流曲线，各种工况电磁转矩的峰值，如表1所示，以便分析机组的疲劳损耗。

1.4 单相重合闸电机动态响应及疲劳损耗分析

根据发电和电动两种工况下的单相故障重合闸过程的仿真结果，对抽水蓄能电机进行强度分析及寿命计算[7]。为此建立发电机定子机座及铁心整体有限元模型，计算单相重合闸过程的电磁转矩对定子机座的影响，得到定子机座动态应力结果。以定子机座材料的S-N曲线作为疲劳计算的基础，应用“雨流法”统计动态应力的循环次数，通过 Miner损伤理论预测发电机的疲劳损耗和寿命。

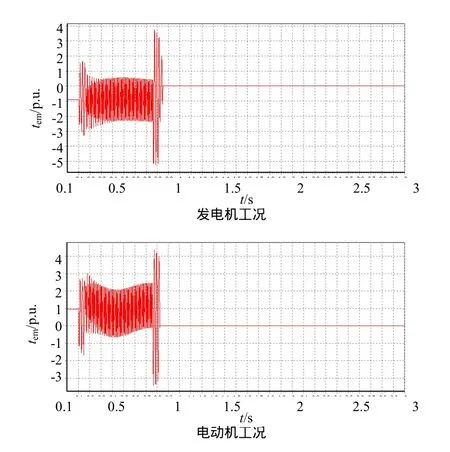
图6 A相不成功重合闸的电磁转矩曲线

表1电磁转矩峰值

图7 定子机座的应力分布

在有限元分析中考虑了单相重合闸时定子机座所受到的电磁转矩、热应力及上机架径向力，且阻尼比取0.05。对表2中最危险的情况（发电工况不成功重合闸——0.76s合闸，0.82s切除）进行分析，结果主立筋倒角处是结构的最危险部位，如图 7所示。主立筋倒角处应力随时间变化曲线如图8所示。采用“雨流法”统计主立筋倒角处的应力循环次数，统计结果如图 9所示。采用线性米勒法对发电机疲劳寿命进行计算（设计S-N曲线如图10所示）。发生一次单相重合闸，主立筋倒角处的疲劳损耗为0.024%，最大应力为240MPa，最大应力出现在0.999s。

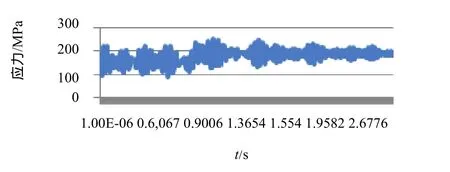
图8 主立筋倒角处应力-时间曲线

根据计算结果可知，一次单相重合闸会在抽水蓄能电机的定子机座引起疲劳损耗，虽然比较小，仍应引起人们注意。

2 结论

本文对抽水蓄能电机的发电和电动两种工况下成功和不成功单相重合闸过程进行了仿真分析，给出了电磁转矩随时间变化曲线及重合闸相的电流变化曲线，并对定子机座和铁心整体进行了强度分析及寿命计算。计算结果为发生一次单相重合闸，主立筋应力集中处的疲劳损耗为 0.024%。这表明单相重合闸会在抽水蓄能电机上引起疲劳损耗，虽然比较小，仍应引起人们注意。这对电机设计的优化及电力系统单相重合闸操作具有指导意义。

图9雨流法计算循环次数

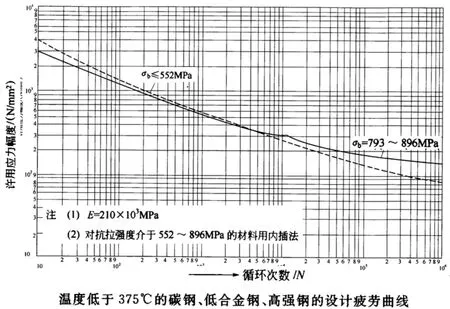
图10主立筋的设计疲劳曲线

附录

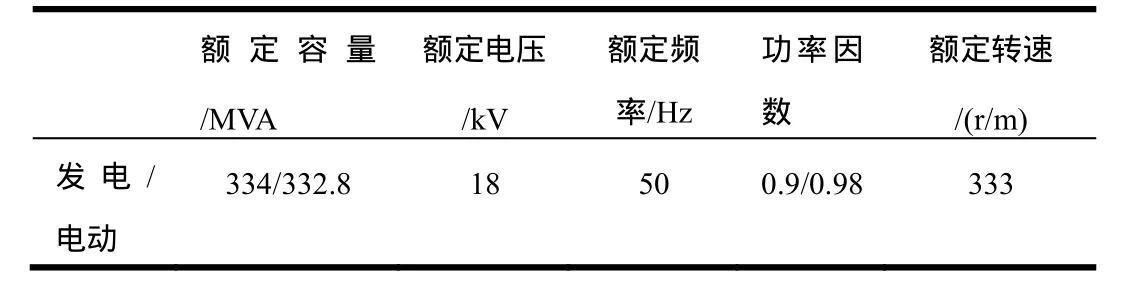
附表1 抽水蓄能电机主要参数

附表2 主变压器参数

附表3 线路参数p.u.

[1] 袁越，张保会. 电力系统自动重合闸研究的现状与展望[J]. 中国电力, 1997(10), 44-48.

[2] 李金香, 孙玉田, 蒋宝钢.超高压发电机短路特性和参数计算[J].大电机技术, 2008(6), 1-5.

[3] 李桂芬, 孙玉田, 张春莉.抽水蓄能电机静止变频启动的仿真[J].大电机技术2010(3), 10-13.

[4] Collins J A. fatigue of materials in mechanics design [M]. New York: Wiley, 1981.

[5] John S. J., et al, The Impact of High Speed Reclosure of Single and Multiphase System Fault on Turbine generator Shaft Torsion Fatigue. IEEE Trans. On Power Applications and Systems,Vol.PAS-99, No.1, pp. 279-291, Jan./Feb.1980.

审稿人：李志和

The Fatigue Life Research for Pumped-storage Stator in Single-phase-reclosing

LAN Bo, LI Jinxiang, YI Ran, LI Bo, WANG Xiaopeng
(State Key Laboratory of Hydro-power Equipment, Harbin 150040, China)

In modern power system, reclosing operation of single-phase fault is commonly employed in order to improve operating stability and reliability. However, the successive electrical transients caused by system faults and subsequent switching operations give rise to mechanical stresses nearby electric machines. These stresses may exceed the endurance limit of certain machine parts and bring about slight and severe fatigue damage which is cumulative over the life of machines.In this paper, the sophisticated simulation model, including an infinite grid, lines, breakers,transformers, synchronous machines and mechanical shaft systems etc., is established to identify an interaction between system and machines. A line to ground fault and the single-phase-reclosing processes (SPRP) are simulated for both generator and motor conditions of pumped-storage machine(PSM). Electric-magnetic torque characteristics and stator current curves are given. The whole stresses of stator core and frame are calculated by FEM and fatigue loss is predicted. The results show that although there is some fatigue in parts, the impact of SPRP on PSM is acceptable. Thus,the structure of machines can be optimized, and an operating guidance will be achieved to SPRP of PSM.

single-phase-reclosing processes; FEM; fatigue loss; pumped-storage machine

TM312

1000-3983(2014)03-0008-04

2013-12-15