Boost变换器的参数选择与非最小相位分析

皇金锋， 刘树林

(1.西安科技大学电气与控制工程学院，陕西西安 710054;2.陕西理工学院电气工程学院，陕西汉中 723003)

其中图3所示的脉冲函数波形f1(t)及小信号扰动分量 φ^(t)的数学表达式为［8］

注:由Boost变换器稳态平衡条件知

0 引言

Boost变换器具有升压功能，同时其功率开关管一端与输入电源共地，其驱动电路设计更容易等优点，在光伏发电系统、新能源应用等许多领域具有广泛的应用前景，研究对其性能改善和控制策略优化是一个热点。Boost变换器以电容电压作为输出量进行反馈控制时，是一个非最小相位系统，表现为小信号数学模型中存在复平面右半平面的一个零点。这个零点的一个显著的特征就是在占空比突变的情况下，除发生超调外，输出电压在开始阶段，会出现先下降后上升(或先上升后下降)的变化，即出现负调现象，这种负调现象会恶化控制系统的动态品质，导致系统的过渡过程时间延长，而且在负调时间段内，控制器接受到相反的反馈信号，形成正反馈系统，严重的影响系统的暂态性能及稳态性能［7］，因此对Boost变换器而言抑制负调尤为重要。

为了改善Boost变换器的控制性能，文献［1］采用了串级结构控制器改善其控制性能;文献［2－5］提出采用非线性控制思路来提高其控制系统性能。以上文献从控制策略方面提高Boost变换器的系统性能。分析Boost变换器数学模型可以看出，引起其非最小相位反应与变换器参数设计有关系，关于参数对非最小相位引起的负调现象文献［6］对准Z源逆变器的内在特性及不同组件容量对逆变器性能的影响;文献［7］对Boost变换器右半平面零点的物理意义进行了深入分析。基于以上分析，本文从Boost变换器参数设计角度探讨提高暂态性能以及减小非最小相位所引起的负调现象，给出抑制或减小负调与参数设计之间的关系，以便在设计和元件选择上进一步提高变换器的性能，减小非最小相位负调对系统的影响，对Boost变换器的优化设计，具有重要指导意义。

1 Boost变换器脉冲波形积分法建模分析

Boost变换器电路拓扑如图1所示。

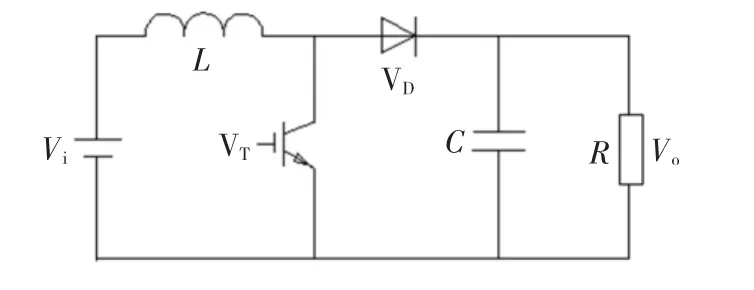
图1 Boost变换器Fig.1 Boost converter

Boost变换器随着开关管的导通与关断其电路的工作模态呈周期性变化，这使得传统的线性分析思路无法进行建模分析［8］。本文采用参考文献［8－11］提出的脉冲波形积分法对其进行建模，其建模的思路是在已知变换器的电路拓扑和工作脉冲波形的条件下，引入非连续周期性脉冲函数，用周期性脉冲函数将变换器在一个周期的各个子电路拓扑统一成一个拓扑，依此拓扑建立开关变换器的小信号模型［8－11］。Boost变换器工作在电感电流连续模式(CCM)时对应图2所示的2个电路子拓扑。

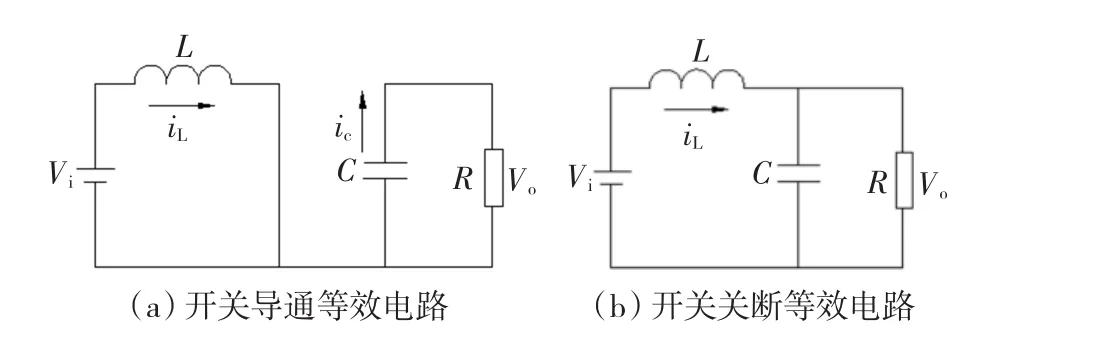
图2 CCM Boost变换器工作模态Fig.2 CCM Boost converter mode

Boost变换器由于功率开关器件VT及功率二极管VD的导通与关断，其电路拓扑呈周期性变化，可以利用图3所示脉冲函数将变换器在一个周期中将两个子电路拓扑统一成一个电路拓扑。

图3 CCM脉冲周期波形Fig.3CCM Pulse waveform

利用图3所示的脉冲周期波形将流过功率开关器件VT的电流利用脉冲函数f1(t)变换为电流源，将功率二极管VD两端电压利用脉冲函数f1(t)变换为电压源，这样就可以将图2所示的2个子电路拓扑统一成为一个电路拓扑，如图4所示。

图4 CCM Boost变换器统一电路拓扑Fig.4 CCM Boost converter circuit topology uniform

根据图4给出的统一电路拓扑，可以列写状态方程为

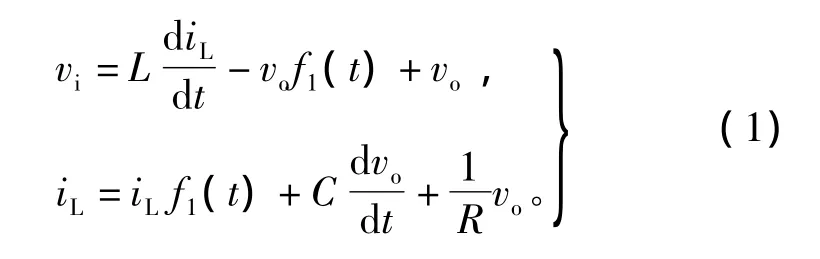
其中图3所示的脉冲函数波形f1(t)及小信号扰动分量 φ^(t)的数学表达式为［8］

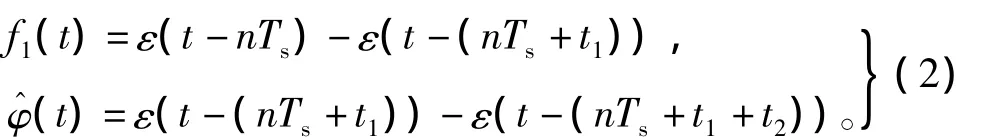
式(1)引入小信号扰动量，此时图4中各支路的变量就由稳态分量和小信号动态分量两部分组成，如式(3)所示，其中“^”表示小信号分量。

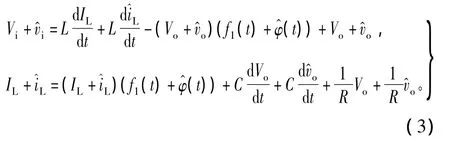
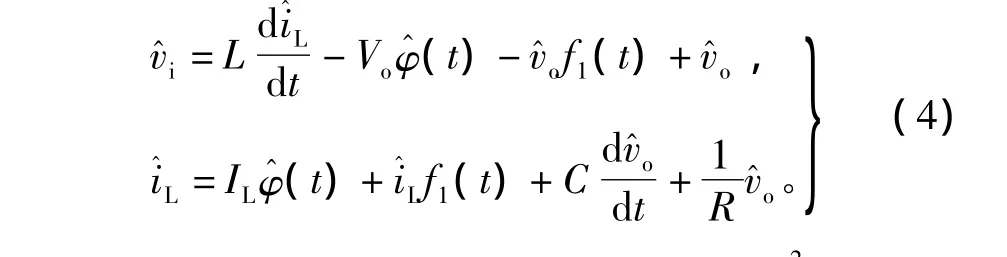
注:由Boost变换器稳态平衡条件知

对式(4)取拉氏变换。根据参考文献［8］可知图3所示的脉冲波形所围成的面积实际上等于该小信号采样值与e－st乘积在这个周期的积分，所有脉冲之和即为该采样函数的拉氏变换［8－11］。因此式(4)中的小信号分量拉氏变换结果为

同理可得

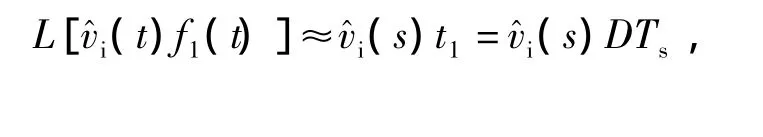
将上面拉氏变换的结论代入式(4)得

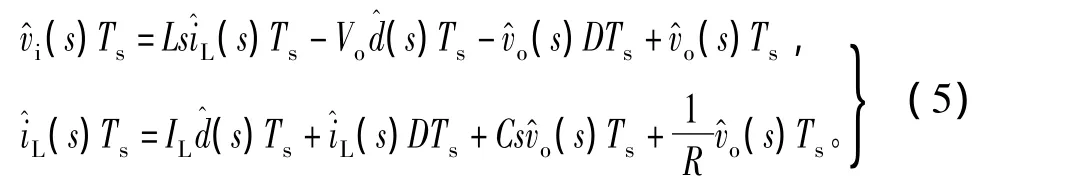
将式(5)进行化简，可得

由式(6)可得CCM Boost变换器输入－输出的小信号动态数学模型为

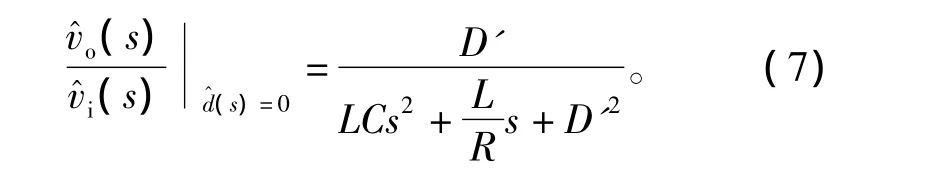
同理，可由式(6)得CCM Boost变换器控制－输出的小信号动态数学模型为

由上面建模结果可以看出，Boost变换器输入－输出数学模型即式(7)为最小相位系统，其决定了变换器启动时暂态特性;而式(8)表明该系统用于设计控制系统的数学模型为一个非最小相位系统，即数学模型含有一个右半平面的零点，该零点会对系统输出电压因电路参数不同将有不同的影响，下文将对此进行详细分析。

2 非最小相位与电路参数之间关系分析

由建立的数学模型分析可以看出，输入－输出数学模型决定系统启动暂态性能，即电感L、电容C、负载R等共同决定系统启动时的超调量、过渡过程时间、上升时间等;而用于设计控制系统的控制－输出的数学模型表明该系统有一个右半平面的零点，在S平面中，右半平面的零点位置随着Boost变换器的电感L、负载R及占空比D的变化而变化。这些参数的变化会引起Boost变换器的振荡和非最小相位反应。为了具体说明这些参数的影响，针对具体一组变换器参数进行说明，并且在保持其他参数不变的情况下只改变其中一个参数，画出不同的零、极点根轨迹图，根据其根轨迹及电路仿真来研究同一电路元件中不同参数对系统输出电压的影响情况［6］。

2.1 电感L对系统的影响分析

取Boost变换器参数:输入电压Vin=12 V、电容C=470 μF、负载R=5 Ω，占空比D=0.4、开关频率fs=50 kHz。下面就工作在CCM下不同电感量(L=100 μH、1 000 μH、3 000 μH)分别进行讨论。采用仿真软件PSIM6.0进行仿真分析，仿真结果给出系统启动过程和稳定运行时占空比突变(在40 ms时占空比由0.4突变为0.5，在70 ms时由0.5突变为0.4)的情况下输出电压的变化情况。图5给出不同电感值对应系统的根轨迹，图6给出不同电感值系统启动过程及系统非最小相位反应。

图5 不同电感值对应的零、极点根轨迹Fig.5 Pole-zero locus of the different inductance value

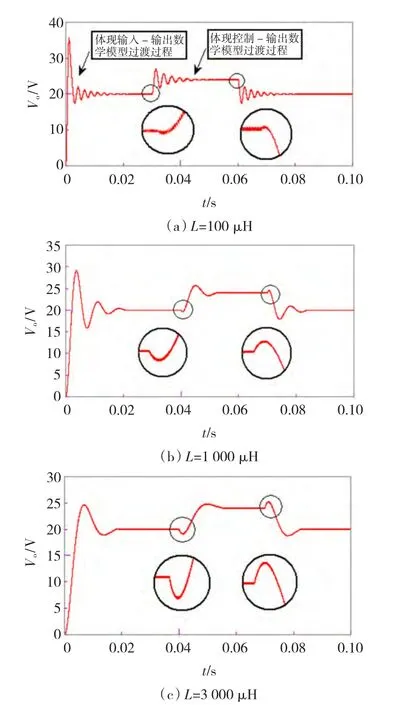
图6 不同电感值对应的系统启动及非最小相位反应Fig.6 System start and Non-minimum phase response in different inductance value

由图5分析可以看出，随着电感量从100 μH到3 000 μH增大，系统在S平面左半平面的极点和右半平面的零点随电感量增大而靠近原点。由图6仿真结果可以看出，体现系统输入－输出数学模型的动态过渡过程随着极点向原点移动，系统的过渡过程超调量减小，振荡频率减小，即仿真结果和实际参数变化关系一致;体现控制－输出数学模型(占空比突变)的过渡过程随着极点和零点向原点靠近，系统的过渡过程超调量减小，振荡频率减小，同时系统的负调现象(右半平面零点引起)随着电感量的增加而更加严重，即当占空比增大(减小)时输出电压没有立刻增大(减小)，反而先减小(增大)而后增大(减小)，而且随着电感量增大负调现象越严重，这一点与右半平面非最小相位特征是一致的。

2.2 电容C对系统的影响

取Boost变换器参数:输出电压Vin=12 V、电感L=100 μH，负载R=5 Ω，占空比D=0.4、开关频率fs=50 kHz。工作在CCM下不同电容量(C=100 μF、470 μF、1 000 μF)在50 ms时D由0.4突变为0.5。图7给出不同电容值对应系统的根轨迹，图8给出不同电容值系统启动过程及系统非最小相位反应。

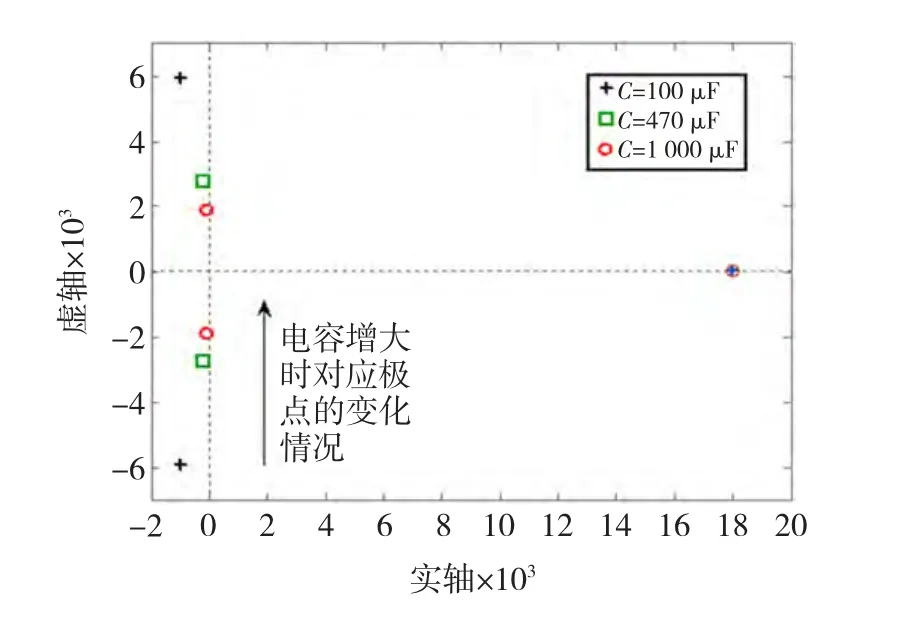
图7 不同电容值对应的零、极点根轨迹Fig.7 Pole-zero locus of the different capacitance value

由图7分析可以看出，随着电容量从100 μF到1 000 μF增大，系统在S平面右半平面的零点位置没有发生变化，而左半平面的极点随电容量增大而靠近原点。由图8仿真结果分析可以看出，随着极点向原点移动，系统的过渡过程时间延长;由图8(a)、图8(b)比较可以看出，随着电容量增大，输出电压的纹波由1.5%降为0.3%，即电容量越大，纹波越小;同时由图8可以看出，随着电容量的增大系统非最小相位引起的输出电压负调没有发生改变，这一点与右半平面零点没有发生变化是一致的，即负调现象不随电容量变化而发生变化［13］。

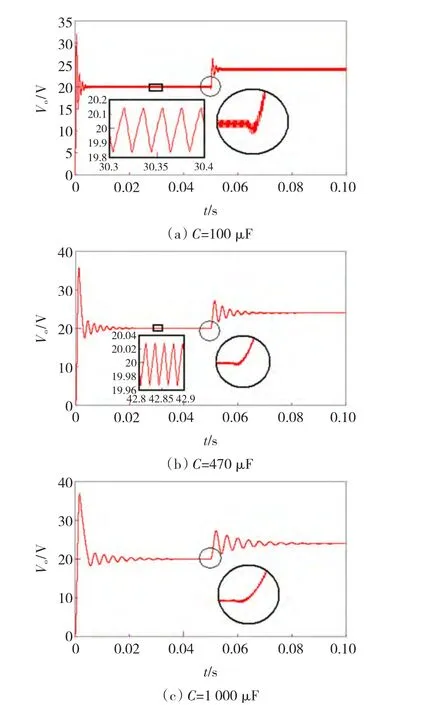
图8 不同电容值对应的系统启动及非最小相位变化Fig.8 System start and Non-minimum phase response in different capacitance value

2.3 负载R对系统的影响

取Boost变换器参数:输入电压Vin=12 V、电容C=470 μF、电感L=100 μH占空比D=0.4、开关频率fs=50 kHz。工作在CCM不同负载(R=5 Ω、1 Ω、0.5 Ω)，占空比变化Δd=0.1。图9给出不同电阻值对应系统的根轨迹，图10给出不同电阻值系统启动过程及系统非最小相位反应。

图9 不同电阻值对应的零、极点根轨迹Fig.9 Pole-zero locus of the different resistance value

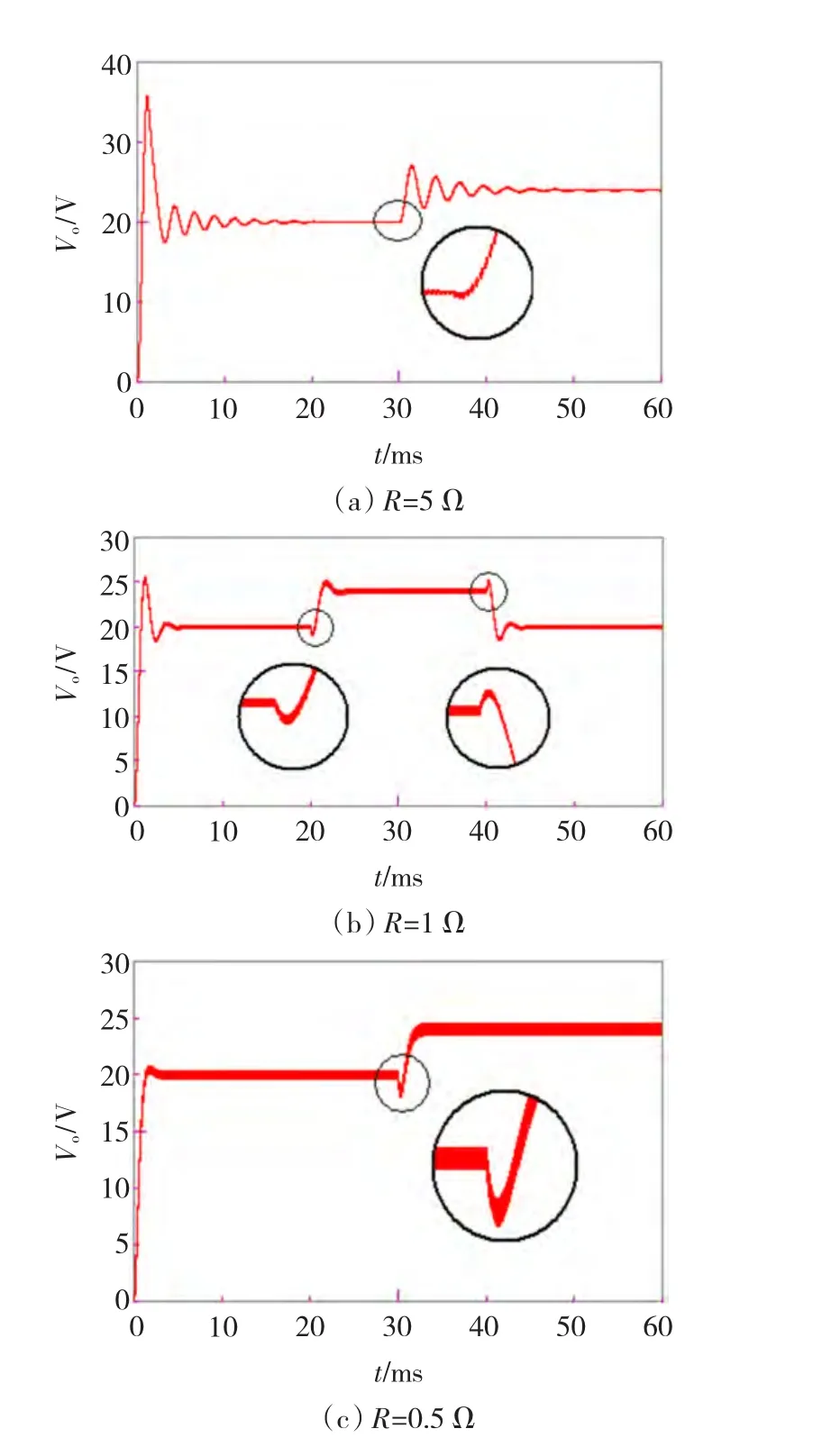
图10 不同电阻值对应的系统启动及非最小相位变化Fig.10 System start and Non-minimum phase response in different resistance value

由图9看出，随着负载阻值由5 Ω减小到0.5 Ω，系统在S平面右半平面的零点靠近原点、左半平面的极点沿虚轴靠近原点，沿实轴远离原点。由图10看出，随着极点向原点移动，系统的过渡过程超调量减小;随着零点向原点靠近，系统的负调现象更加严重。即负调随着负载的加重而加剧。这一点与上面数学模型关于非最小相位特征是一致的。

2.4 占空比D对系统的影响

取Boost变换器参数:输入电压Vin=12 V、电容C=470 μF、电感L=100 μH、负载R=5 Ω、开关频率fs=50 kHz。工作在CCM不同的占空比(D=0.1、0.3、0.5)，占空比变化 Δd=0.1。图11给出不同占空比对应系统的根轨迹，图12给出不同占空比系统启动过程及系统非最小相位反应。

由图11看出，随着占空比D由0.1增加到0.5，系统在S平面右半平面的零点靠近原点、左半平面的极点靠近原点。由图12看出，随着极点向原点移动，系统的过渡过程超调量增大，过渡过程时间延长;随着零点向原点靠近，系统的负调现象虽然有增加，但是不明显，其主要原因是占空比变化最大范围Dmax≤1，其变换范围太小(和电感、电容的参数变化相比较)，所以由占空比引起的负调现象并不明显。

图11 不同占空比对应的零、极点根轨迹Fig.11 Pole-zero locus of the different Duty cycle

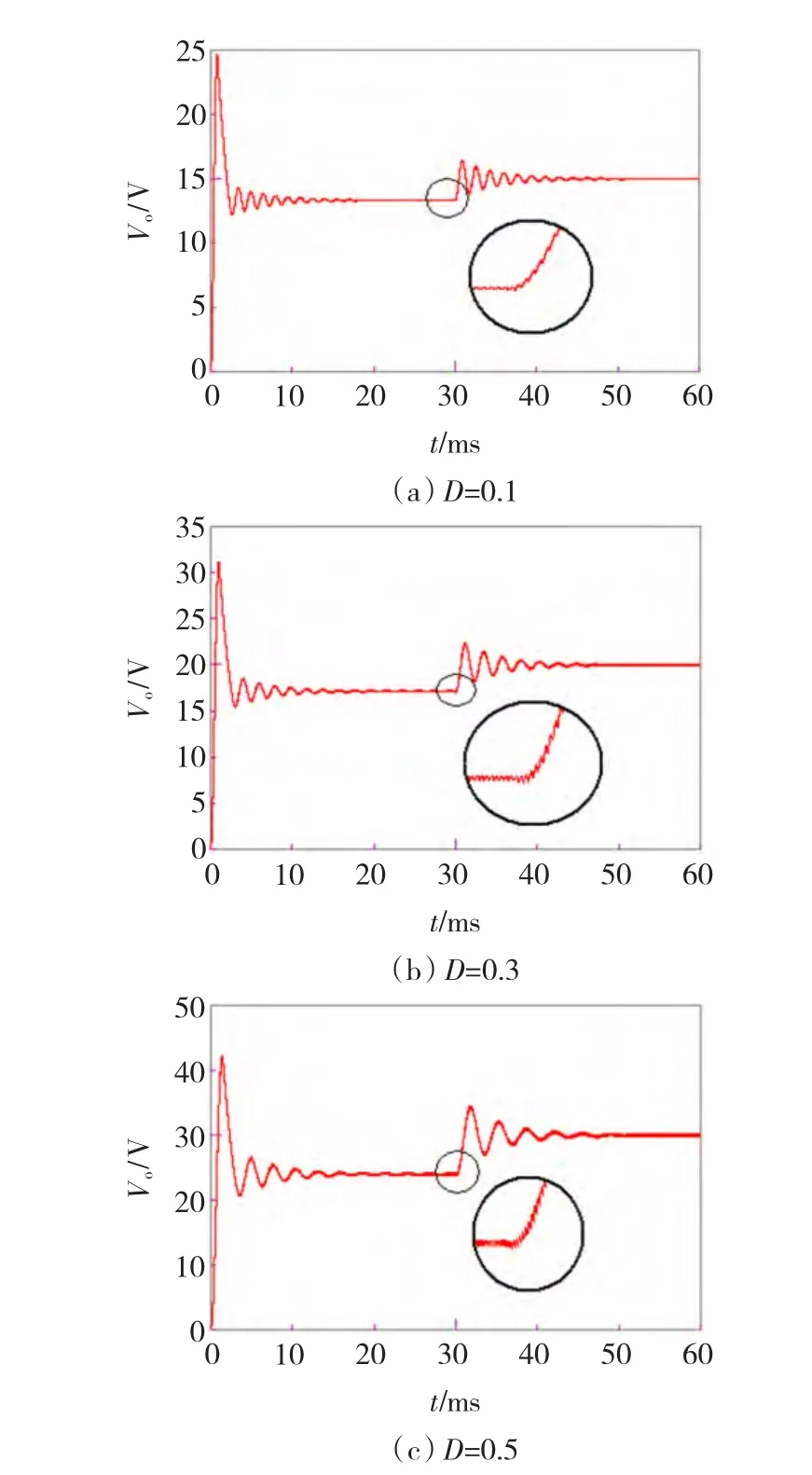
图12 不同占空比对应的系统启动及非最小相位变化Fig.12 System start and Non-minimum phase response in different Duty cycle

3 变换器参数选择与暂态性能优化设计

由第2节分析可以看出，Boost变换器的启动暂态性能主要由电感、电容、负载共同来决定，而系统非最小相位反应即负调现象由电感、占空比、负载等共同决定。如何对这些参数进行优化设计，使得系统即能满足启动暂态响应，又能兼顾非最小相位引起的负调现象是一个关键问题。根据Boost变换器已有的研究成果［12］对其进行优化设计。为了获得系统整体优化设计思路，首先对每个影响系统暂态性能的参数进行分析，进而总结给出系统总体参数优化设计思路。

3.1 不同电路参数对系统暂态性能的影响分析

由第2节分析可以看出，电感、电容、占空比、负载等对系统暂态响应都有影响，下面分别就其对系统暂态影响进行具体分析。

1)电感对系统影响分析

［12］知，Boost变换器根据电感电流的最小值是否等于零，将其工作模式划分为电感电流连续模式(CCM)和电感电流断续模式(DCM)两种模式，其临界电感取值为LC。但是工作在CCM的Boost变换器根据电感电流的最小值与输出电流的比较，可以将其划分为电感完全供能模式(CISM)和电感不完全供能模式(IISM)，其临界电感取值为LK。其临界电感LC和LK计算式为

由式(9)、式(10)可以看出，工作在CCM的电感仅当负载和占空比不变时，适当提高开关频率就可以减小临界电感取值，由2.1节分析可知，减小电感取值就可以减小非最小相位引起的负调。

2)电容对系统影响分析

由2.2节分析可知，Boost变换器系统输出电压的负调与电容选择大小没有关系，不同的电容取值会影响输出电压纹波(即电容越大，输出电压纹波越小)和系统的暂态过渡过程。同时由文献［12］知，输出电压纹波具有以下特点:工作在CCM－CISM输出电压纹波最小且与电感无关，其纹波电压大小为

由式(11)可以看出，在开关频率、负载、输出电压和占空比不变的情况下，工作在CCM－CISM输出电压纹波随电容增大而减小，与电感选择大小没有关系。

3)占空比对系统影响分析

由2.4节分析可以看出，占空比变化引起的负调现象并不明显，主要原因是占空比变化范围太小(和电感、负载参数变化相比较)，同时，Boost变换器输出电压大小由占空比决定，因此，占空比一般不做为优化参数。

4)负载参数对系统影响分析

一般对Boost变换器而言，其所带的负载一般属于某一个范围{Rmin～Rmax}。由2.3节分析可以看出，负载最重(即阻值取Rmin)，系统输出电压所对应的负调现象最严重，输出纹波电压最大(即对应电容选择满足纹波要求所取最小电容Cmin);由式(9)、式(10)分析可以看出，负载越轻(即负载阻值取Rmax)，对应CCM临界电感取值最大(即对应临界电感最小值Lmin)。因此由负载参数变化范围可以确定最小临界电感Lmin，最小滤波电容Cmin。

5)开关频率对系统影响分析

由上面的小信号数学模型可以看出，开关频率与系统的启动过程及非最小相位引起的负调反应没有明显的关系，但是通过3.1节第1)部分电感分析可以看出，当提高开关频率时，由式(9)、式(10)分析看出，可以减小LC和LK电感取值，减小临界电感取值意味着扩大了变换器设计电感取值范围，由2.1节分析可以看出，较小的电感取值更有利于减小负调反应，而且较大的电感取值范围同时可以兼顾启动特性。由2.2节分析可以看出，增大或减小电容不会引起系统非最小相位反应(即负调现象)变化，但是，由式(11)可以看出，增大开关频率可以减小纹波，即满足系统要求纹波的前提下，通过提高开关管频率就可以减小电容取值，相当于扩大变换器设计时的电容取值范围，较大的电容取值范围更方便对系统暂态性能进行优化设计。虽然提高开关频率可以间接的改善系统的启动及非最小相位反应，但是开关管的频率提高受开关器件、变换器转换效率及电磁兼容等方面情况影响，所以在一定范围内提高开关频率可以间接优化系统暂态性能和非最小相位反应。

3.2 变换器整体参数优化设计分析

Boost变换器系统参数整体优化须兼顾启动暂态性能及非最小相位带来的负调现象、系统的品质因子、输出电压纹波、开关工作频率以及变换器自身谐振频率之间关系等方面进行整体参数优化设计。由第2节参数分析可以看出，影响Boost开关变换器启动暂态性能及非最小相位反应负调现象的因素很多，即待优化参数较多。但是通过3.1节分析可以看出，由于占空比和负载不能优化设计，那么可待优化的参数即电容和电感。由前面电容分析可以看出，工作在CCM－CISM的变换器输出纹波电压与电感量选择无关，利用这一特点，电感选择时将其设计在CCM－CISM区域(电感量越接近LK，即电感量越小，其引起的负调现象越弱)，这样电感选择就可以不用考虑输出纹波电压对系统的影响。同时由2.2节参数分析知电容对非最小反应负调现象没有影响，那么电容选择则主要考虑输出纹波电压的要求。由式(11)知变换器输出电压的最大纹波量就决定了最小电容Cmin。利用以上电感和电容的特点，选择电感和电容时可以单独考虑而不用考虑其相互影响。如果电感和电容不满足系统参数优化设计指标要求，则可以通过提高开关工作频率来扩大其选择范围，来满足系统启动暂态性能及非最小相位即负调反应等性能指标要求［13－14］。

4 参数选择优化实验验证

4.1 参数优化设计仿真验证

为了验证上面提出Boost变换器参数优化设计思路及优化方法正确性，文中给定一组变换器参数进行优化并进行仿真验证。Boost变换器参数为:输入电压Vin=12 V;负载R=5～50 Ω;输出电压Vo=20 V;纹波电压ΔVo≤200 mV;系统负调电压ΔVF≤500 mV。

由上面给出的输出电压可以计算出D=0.4。待优化参数为:电感L、电容C、开关管工作频率fs。首先设定开关工作频率fs=100 kHz，则由纹波电压ΔVo≤200 mV可以根据式(11)计算出滤波电容的最小值Cmin=80 μF。当负载最轻(即R=50 Ω)时对应电感处于CCM－CISM范围的最小值，由式(12)可以计算出Lmin=LK=90 μH，只要选择电感量大于90 μH，此时Boost变换器就工作在CCMCISM。综合系统的品质因子、输出电压纹波、非最小相位负调反应等因素，文中选择C=100 μF、L=100 μH、最重负载R=5 Ω(即最大纹波及最大负调现象)，进行仿真结果验证。仿真思路和占空比变化同2.1节电感参数变化选择思路一致。仿真结果如图13所示。

仿真结果表明:将电感选择在CCM－CISM，保证了系统输出纹波电压小于200 mV，同时当系统占空比由0.4突变为0.5或由0.5突变为0.4，系统负调电压限制在500 mV以内，系统过渡过程时间大大缩短，在5 ms内已基本稳定。仿真结果表明:文中提出的Boost变换器参数优化设计思路及优化方法的正确性。

图13 优化后系统启动及非最小相位的影响Fig.13 System start and Non-minimum phase response after optimization

4.2 参数优化设计实验验证

Boost变换器参数为:输入电压Vin=14 V;开关频率fs=100 kHz;负载R=5 Ω;电容C=100 μF;占空比D=0.4。由于开关器件等电路损耗，因此当输入电压为Vin=14V时输出电压不是23.3 V，实际输出电压为20 V。为了更明显的观察当系统占空比发生变化时的效果，将占空比由D=0.4突变为D=0.6。电感取不同值(L=20 mH、10 mH、100 μH)时表现出不同的负调响应，实验结果如图14所示。

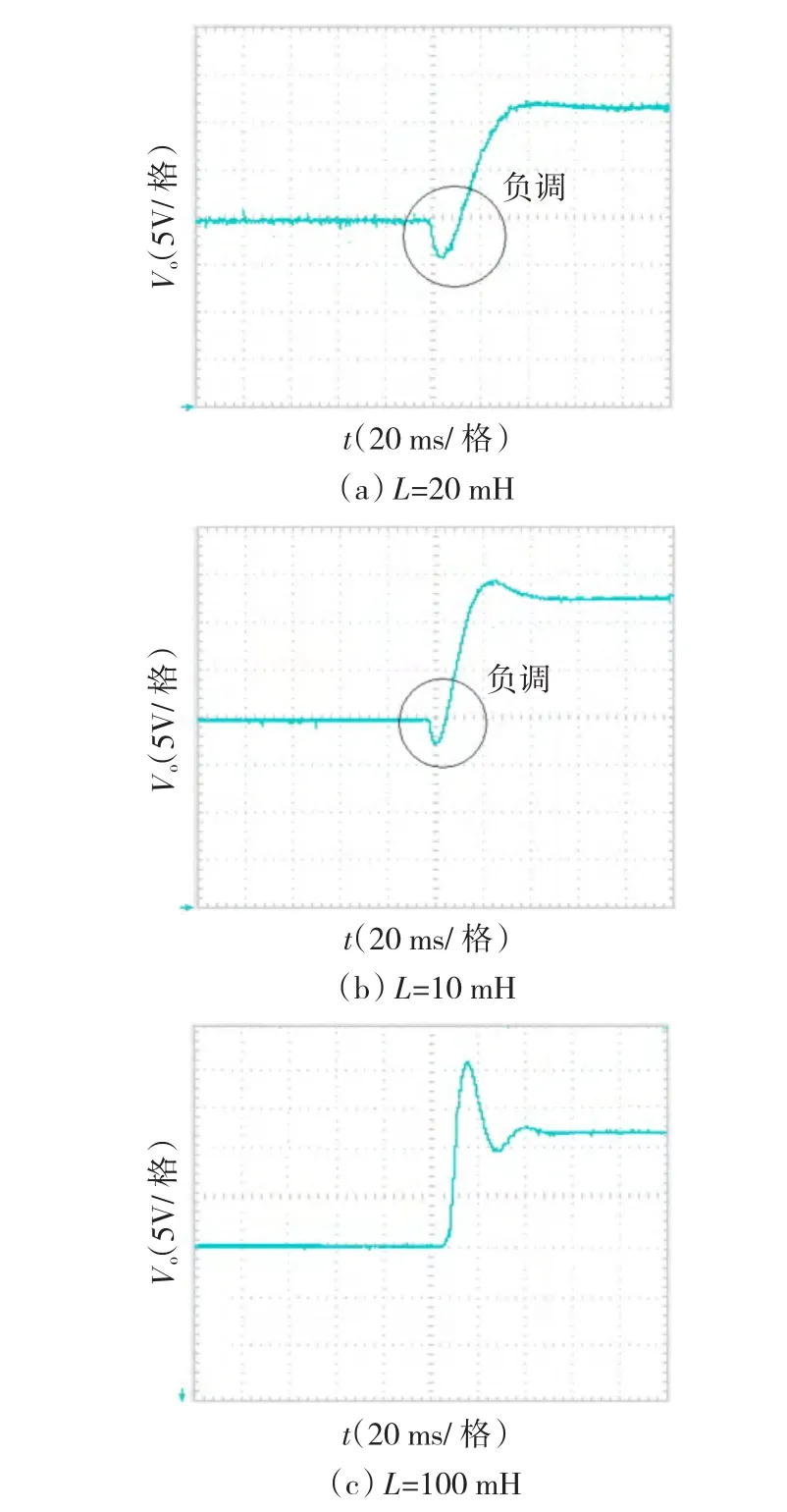
图14 不同电感值对应的系统非最小相位变化Fig.14 Non-minimum phase response in different inductance value

实验结果分析:将电感选择在CCM－CISM后，电感取L=20 mH时，系统输出负调电压ΔVF=4 V，当电感取L=10 mH时，系统输出负调电压ΔVF=3 V，当电感取L=100 μH时，系统输出电压负调已基本没有。实验结果表明:文中提出的Boost变换器参数选择与优化设计方法的正确性。

5 结语

本文利用脉冲波形积分法建立了Boost变换器工作在CCM的小信号动态数学模型，根据建立的数学模型详细讨论了电感、电容、负载、占空比、频率等参数对系统暂态性能和非最小相位引起的负调电压影响，得到以下结论:较大的电感、满载负载、较大的占空比使得系统的非最小相位反应即负调现象更加明显;不同的电容值会影响系统的暂态性能和输出电压纹波，对非最小相位反应没有影响。总结归纳给出提高Boost变换器暂态性能及减小非最小相位反应的参数优化设计思路。仿真和实验结果验证了上述结论。

参考文献:

［1］吴忠，李红，左鹏，等.DC/DC升压变换器串级控制［J］.中国电机工程学报，2001，22(1):110－115.

WU Zhong，LI Hong，ZUO Peng，et al.Cascade control of DC/DC Boost converters［J］.Proceedings of the CSEE，2001，22(1):110－115.

［2］帅定新，谢运祥，王晓刚，等.Boost变换器非线性电流控制方法［J］.中国电机工程学报，2009，29(15):15－21.

SHUAI Dingxin，XIE Yunxiang，WANG Xiaogang，et al.Nonlinear current control method for boost converter［J］.Proceedings of the CSEE，2009，29(15):15－21.

［3］乐江源，谢运祥，洪庆祖，等.Boost变换器精确反馈线性化滑模变结构控制［J］.中国电机工程学报，2011，31(30):16－23.

LE Jiangyuan，XIE Yunxiang，HONG Qingzu，et al.Sliding mode control of boost converter based on exact feedback linearization［J］.Proceedings of the CSEE，2011，31(30):16－23.

［4］刘锦波，明文龙.一种基于输入/输出反馈线性化的Boost型DC/DC变换器非线性控制方案［J］.中国电机工程学报，2010，30(27):55－61.

LIU Jinbo，MING Wenlong.A novel scheme of nonlinear control strategy based on input-output linearization for Boost type DC/DC converter［J］.Proceedings of the CSEE，2010，30(27):55－61.

［5］何金梅，郑雪梅，王卫，等.Boost变换器混沌现象的非奇异终端滑模控制方法［J］.电工技术学报，2013，28(4):104－108.

HE Jinmei，ZHENG Xuemei，WANG Wei，et al.Terminal sliding mode control of Boost converter with chaos［J］.Transactions of China Electrotechnical Society，2013，28(4):104－108.

［6］蔡春伟，曲延滨，盛况.准Z源逆变器的暂态建模与分析［J］.电机与控制学报，2011，15(10):7－13.

CAI Chunwei，QU Yanbin，SHENG Kuang.Transient modeling and analysis of quasi-Z-source-inverter［J］.Electric Machines and Control，2011，15(10):7－13.

［7］张卫平.开关变换器的建模与控制［M］.北京:中国电力出版社，2006.

［8］高潮，邱关源.谐振型变流器建模的脉冲波形积分法［J］.重庆大学学报，1994，17(5):1－6.

GAO Chao，QIU Guanyuan.An approach of pulse waveform integral to modeling resonant converters［J］.Journal of Chongqing Uinversity，1994，17(5):1－6.

［9］高潮，邱关源.直流电－直流电开关变流器的统一建模方法［J］.电子学报，1995，23(2):53－58.GAO Chao，QIU Guanyuan.A unified approach to mode DC－DC switching converters［J］.ACTA Electronica Sinica，1995，23(2):53－58.

［10］高潮，邱关源.准谐振及PWM型变流器开关工作波形平均建模法［J］.电工技术学报，1996，11(1):38－42.

GAO Chao，QIU Guanyuan.Switching waveforms averaging approach to modeling quasi-resonant and PWM converters［J］.Transactions of China Electrotechnical Society，1996，11(1):38－42.

［11］胡宗波，张波，方珂，等.三电平DC－DC变换器的统一建模研究［J］.电路与系统学报，2005，10(1):64－69.

HU Zongbo，ZHANG Bo，FANG Ke，et al.Uinfied modeling study of three-level DC-DC converters［J］.Journal of Circuits and Systems，2005，10(1):64－69.

［12］刘树林，刘健，杨银玲，等.Boost变换器的能量传输模式及输出纹波电压分析［J］.中国电机工程学报，2006，26(5):119－124.

LIU Shulin，LIU Jian，YANG Yinling，et al.Energy transmission modes and output ripple voltage of boost converters［J］.Proceedings of the CSEE，2006，26(5):119－124.

［13］KAPAT S，PATRA A，BANERJEE S.A current-controlled tristate boost converter with improved performance through RHP zero elimination［J］.IEEE Transaction on Power Electronics，2009，24(3):776－786.

［14］徐德鸿.电力电子系统建模及控制［M］.北京:机械工业出版社，2006.